灾区应急物流的动态配送模型及案例分析

丁旭宁

（浙江财经大学，浙江 杭州 310018）

灾区应急物流的动态配送模型及案例分析

丁旭宁

（浙江财经大学，浙江 杭州 310018）

回顾了灾区应急物流的研究现状，并提出建立应急物流的动态配送模型，指出其包括三个步骤，分别是制定初始计划、制定配送方案与二次调整配送方案。接着构建了灾区应急物流的配送中心选址模型和二级配送中心模型，利用典型案例验证物流动态配送模型的实用性。

应急物流；动态配送模型；二级配送模型

1 引言

我国是一个受灾较为频繁的国家，如何科学防灾减灾值得深入探讨。本文对灾区应急物流系统进行研究，为应对突发事件的物资配送提供一定的指导。灾区应急物流与普通物流存在一定的相似性和不同性。相似性在于配送的目标都在于以最低的成本完成配送任务，一方面，两者追求的侧重点不同，灾区应急物流更重视及时性，强调配送效率第一、成本效益第二；而普通物流追求的是利益最大化。另一方面，两者的动态变化程度不同，灾区应急物流配送中心在不同周期内会改变，而普通物流的配送中心是固定的。灾区应急物流的动态配送中心随着受灾区域的增加而增加，配送的目的地也会动态变化。因此，灾区应急物流配送需要考虑动态变化，采用动态配送模型能更有效地完成灾区应急物流配送任务。

2 灾区应急物流研究现状

灾区应急物流主要是针对突发性事件中物资配置要求而产生的，主要涉及应急物流配送中心选址、突发事件处理以及应急物资配送路径规划、应急物资配送等。一般来说，灾区应急物资配送点是以服务站、救援点等形式存在，在突发事件之前预先建设应急物流配送中心，确保应急物资在第一时间内送达到灾区。灾区应急物流动态配送及路径规划是灾区应急物资处理的核心内容，即以配送时间为第一要件，完成应急物资配送。

目前，国内外学者针对应急物流配送的研究主要集中在静态配送模型，而对于动态配送模型的研究较少。静态配送无法应对灾区应急物流动态变化的特点，也难以实现在最短时间内以最优路径配送应急物资的目标。无论是灾区的物资配送点还是配送量都是随着时间的变化而变化，因此灾区应急物流配送需要建立动态模型，根据灾区的物资需求不断调整配送方案，通过分阶段的方法来实现灾区应急物资的配送服务。动态配送有利于降低灾区的损失，因此研究灾区应急物流的动态配送模型具有较高的理论价值与实用价值。

本文通过对灾区应急物流的内涵进行剖析，分析影响动态配送的各个因素，灾区应急物流的配送时间为第一目标，构建灾区应急物流的动态配送模型，分三个步骤完成灾区应急物流的动态配送，依次是制定初始计划、制定配送方案与二次调整配送方案。

3 建立灾区应急物流动态配送模型

假设G表示动态配送物流网络，令G=（V，E）。其中，V={v1，v2，…，vn}表示节点，E={e1，e2，…，en}表示边。

在m个配送周期n个节点内需求量为Q，那么需求矩阵Q可表示为：

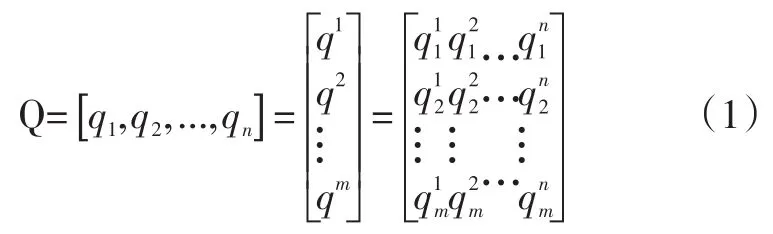
其中，列向量qi表示第i个节点所有的配送需求；行向量qj表示第j个周期内所有需求节点的需求总量。相对而言，灾区应急物流的需求量在不同周期的动态变化要大于普通物流。

第一步，制定初始计划。灾区应急物流动态方案需要设定一个初始计划，选择配送中心的初始节点、初始路线；第二步，制定配送方案，根据配送中心与二级配送模型制定物流方案；第三步，判断应急物流需求是否变化，根据新周期的节点需求特点作相应的调整。

3.1 构建灾区应急物流的配送中心选址模型

假定①灾区应急物流网络共有n个节点，选择其中的m个配送点作为应急移动物流配送中心（m≤n）；②在同一个周期内，节点的需求量不发生变化；③各个节点的配送成本由需求量、与配送中心距离与单位配送成本决定；④应急物流配送按配送点就近原则；⑤应急移动配送点中心负责配送的节点集合应包括所有的物流节点。

令灾区应急物流移动配送中心的应急网络矩阵为H，则H表达式为：

采用floyb算法对应急物流配送中的各个节点最短路径进行计算，选出各物资需求节点到配送中心的最短距离，令L为物资到应急物流配送中心的最短距离矩阵，则L可表示为：

由假设①可确定物资与选择的配送中心的最短路径矩阵L'，则L'可表示为：

其中，li(m+j)表示第i个需求节点与第（m+j）个配送中心的最短距离。

假定配送中心配送的总成本为TC，可计算出总成本公式为：

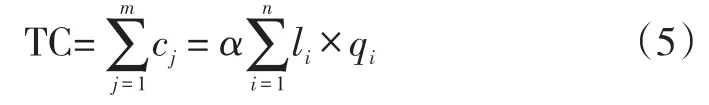
其中，cj表示各个物资到应急物流配送中心的配送成本，li=min{l1i，l2i，…，lmi}表示第i个节点与最近配送中心之间的距离，qi表示第i个需求节点在某个需求周期内的需求量。

由上，建立灾区应急物流中心的选择模型，目标函数及约束条件为：

灾区应急物流动态配送中心的选址的宗旨是满足需求点与获得物资需求的前提下所有救灾物资的配送成本最低。应急物流的首要目标是应急物资到所需物资的时间最短，可转化为此处的目标函数，即救灾物资配送的成本最低。假设物流成本为物流配送的车辆源成本，在单位运输成本与运输速度一定时，配送成本与运输时间成正相关关系，所以此处的目标函数可以转化为成本最低。

3.2 构建二级配送中心模型

为了完成应急移动配送点中心负责配送的节点集合包括所有的物流节点的目标，需要对各个区域的配送路径进行规划，求解各个节点的配送路径。

令Hi表示第i个灾区应急物流的动态配送中心，该配送中心共拥有t辆运输车，第k辆运输车的载重为Qk，其中k≤t，该中心负责的应急物资需求集合为Ui（Ui=i|i= 1，2，…，n）。

首先，根据公式（4）计算应急物资需求集合Ui，则Ui表示为：

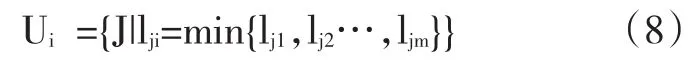
其中，J表示物资需求集合，j表示物资需求点，即第j个物资需求点到灾区应急物流动态配送中心i的最短距离，将所有与灾区应急物流动态配送中心i的距离最短的节点汇总并集合到Ui。

然后，根据上述的假设条件，构建各个灾区应急物流的动态配送路径，满足最急配送目标，即第一时间给最需要的救灾地点配送物资，具体算法如下：

①计算ui（ui∈Ui）

其中，Ej表示物资需求点j要求救灾物资到达的最长配送时间；lji表示物资需求点j与灾区应急物流配送中心i的最短距离，vji表示车辆运输的速度。

②给物资需求点j配送物资，优先给救灾物资到达的最长配送时间与直接配送时间的差最小的物资需求点配送物资。

③判断运输过程中是否经过其他需要物资的节点。若其他节点均已配送，那么n=n-1，并回到①。若其他节点部分未配送，则根据车辆的载重Qk确定是否可配送沿途节点，若载重与需求点之差小于中途节点的需求量，那么n=n-1，并返回①；若可以满足配送，则同时配送，n=n-k。

根据上述的算法，以此类推可计算出灾区应急物流的动态配送中心与救灾物资需求点的配送路线，完成救灾物资的配送需求。

4 案例分析

为了验证上述构建的模型是否具有实用性，本文以一个具体的案例来验证。假设某灾区共有10个救灾物资需求点，即n=10。每辆运输车的载重均为6t，即Qk= 6t。车辆运输的平均速度为40km/h，即vji=60km/h。假定以天为配送周期，每个灾区物资需求点不同时期的需求量与时间要求见表1，必须保证救灾物资及时送达。各个灾区需求点之间的距离见表2。

表1 灾区物资需求点的需求量与时间要求 单位：t/h

注：∞表示两个灾区之间无法直接到达。

利用floyd算法计算灾区应急物流配送中的各个节点的最短路径，获取最短距离矩阵L，根据公式（7）计算灾区的应急物流配送中心。

第一天配送中，获取灾区物流动态配送中心为u6和u8，即将救灾物资配送中心设置在u6和u8这两个需求节点，再根据二级配送模型计算具体的救灾物资配送路线，计算每个应急物流配送中心所负责的物资需求点集合。

利用式（8）可计算出这两个灾区物流配送中心所负责的物流节点，u6负责u2、u5、u7；u8负责u1、u3、u4、u9、u10。

根据最急需求目标，可计算出灾区应急物流第一天配送的子任务的配送路径：

u6子任务u6→u5→u2；u6→u7；

u8子任务u8→u3→u4→u1；u8→u10→u9。

同理，第二天配送中，获取灾区物流动态配送中心为u4和u8，即将救灾物资配送中心设置在u6和u8这两个需求节点，再根据二级配送模型计算具体的救灾物资配送路线，计算每个应急物流配送中心所负责的物资需求点集合。

利用式（8）可计算出这两个灾区物流配送中心所负责的物流节点，u4负责u2、u1、u7；u8负责u3、u5、u6、u9、u10。

根据最急需求目标，可计算出灾区应急物流第一天配送的子任务的配送路径：

u4子任务u4→u1→u7；u4→u2；

u8子任务u8→u3→u10→u9；u8→u3；u8→u6→u5。

从灾区应急物流的动态配送模型的计算结果可以看出，这两个周期的u8均被选为应急物流配送中心，可见该节点在物流配送中处于中心地段，与多个节点的距离均较短，该模型的选址结果与实际配送结果相符。在第二天中，灾区物流需求节点u3出现了2条线路，并且有一条线路仅有一个配送对象，这是为了满足最急需求的优先配送。只有完成配送任务，才能保障灾区及时获取配送物资。由此，可见本文构建的灾区应急物流的动态配送模型具有一定的实用价值。

5 结语

应急物流具有较强的动态性，不同周期灾区应急物流的配送中心与物资需求点都会改变。在考虑满足应急物资配送需求点的同时，要以时间效率为第一要件，同时考虑物流服务中服务对象的重要性因素，在构建灾区应急物流的动态配送模型的同时，构建二级配送模型，确保应急物资准时到达物资需求点。由于不同配送周期，灾区应急物流的配送中心与配送点都是动态变化的，这种变化加大了配送路径制定的难度，需要利用二级配送模型来调整配送路线，满足灾区动态的物流配送需求。本文的研究重点在于优先满足最急的配送任务，配送路线还有待进一步优化改进，最终在完成灾区物流配送任务的同时节约配送资源。

[1]Trevor Hale,Christopher R Moberg.Improving supply chain disaster preparedness decision process for secure site location[J]. International Journal of Physical Distribution&Logistics Management,2005,(5):195-207.

[2]钟慧玲,谢晓飞,张冠湘,等.基于信息扩散模型的危险品道路运输事故率分析[J].物流技术,2014,(5):111-113,144.

[3]朱佳翔,谭清美,蔡建飞,等.基于双重不确定性的应急物流配送策略[J].系统工程,2016,(3):1-8

[4]朱鸿,涂克林,朱伟.动态需求下的多目标配送中心选址研究[J].物流技术,2012,(4):68-70.

A Case Study on Model of Disaster Zone Emergency Logistics Using Dynamic Distribution

Ding Xuning
(Zhejiang University of Finance&Economics,Hangzhou 310018,China)

In this paper,we established the distribution location model and two-stage distribution model for the emergency logistics operations in disaster stricken areas and through a typical case,demonstrated the practicality of the dynamic distribution model.

emergency logistics;dynamic distribution model;two-stagedistribution model

F274

A

1005-152X(2017)01-0085-04

10.3969/j.issn.1005-152X.2017.01.017

2016-11-09

丁旭宁，男，甘肃天水人，浙江财经大学学生，研究方向：数学。