抽水蓄能机组调速系统非线性预测控制方法研究

散齐国，周建中，郑 阳，许颜贺，张云程，张 楚

（1. 江西洪屏抽水蓄能有限公司，江西 靖安 330603；2. 华中科技大学，武汉 430074）

抽水蓄能机组调速系统非线性预测控制方法研究

散齐国1，周建中2，郑 阳2，许颜贺2，张云程2，张 楚2

（1. 江西洪屏抽水蓄能有限公司，江西 靖安 330603；2. 华中科技大学，武汉 430074）

调速系统是抽水蓄能机组频率及出力控制的主要部件，其控制性能及控制品质对于工况变化频繁，在电网中担任削峰填谷任务的抽水蓄能机组尤为重要。本文针对传统抽蓄机组的PID控制器中控制参数受工况影响大，控制器缺乏状态预测能力等缺点，提出一种适用于抽蓄机组调速系统不同工况的快速非线性预测控制方法。该方法应用抽蓄机组全特性曲线作为水泵水轮机模型，考虑压力引水管道的水击现象，利用模糊PID控制与预测控制的滚动状态预测原理计算得到调速器控制信号，使得调速器在根据运行工况精确控制机组频率与出力的同时，保证了控制计算的实时性。通过以某抽水蓄能电站实际资料进行抽水蓄能机组发电方向开机和负荷调节动态过程仿真，结果表明该预测控制方法较传统控制方式效果优越。

抽水蓄能机组；非线性建模；调速控制；非线性预测控制；

0 前言

随着我国电力系统规模不断发展，电网对调峰调频的要求也越来越高。抽水蓄能电站作为优质的调峰调频电源，发挥着调峰填谷，维持电网供需平衡等重要作用[1]。抽水蓄能电站在电网中的作用及其工况转换频繁的运行特点对其调速系统的控制性能提出了更高的要求。目前，工程上主要运用原理简单易行，技术成熟的PID型调速器对抽水蓄能调速系统进行控制，但PID的控制参数取值依赖于运行工况，在抽蓄机组运行状态根据电网需求频繁变动时，很难确定出一组能广泛适应不同工况的参数，且在工况大范围波动情况下，PID控制的实时控制率是根据过去与当前系统信息得出的，缺乏对未来工作状态的预测。针对传统PID型调速器存在的上述不足，许多学者尝试将更先进的控制方式引入水轮机调速系统中，以提高其控制性能。近年来，分数阶 PID 控制[2,3]，模糊控制[4,5]，滑模变结构控制[6]，神经网络控制[7]和模型预测控制[8-10]等先进控制方法相继被应用到水轮机和抽水蓄能机组调速系统控制的研究中，为其控制性能的提高提供了重要思路。其中，模型预测控制因其不拘泥于研究对象的模型形式，对变量约束的显式处理以及有限时域控制优化和状态预测能力等特点受到广泛关注。文献[8]和文献[9]分别将动态矩阵控制和广义预测控制等典型预测控制方法应用到水轮机调速系统中，但由于这些预测控制方法复杂的数学公式推导和控制论方法的应用，只对线性水轮机模型有效，在工程应用上幵不能准确描述实际水轮机工况大范围变化时的运行特性，具有一定局限性。文献[10]提出一种基于引力搜索模糊辨识的水电机组广义预测控制，且在对水轮机建模使用了能描述水轮机强非线性特性的全特性曲线，对水轮机精确控制有一定指导意义，但由于其引水系统水击模型采用刚性水击模型，难以准确刻画长引水管动态特性，且一般水轮机的全特性因工况相对较少远比抽蓄电站的水泵水轮机简单，故该方法也不适用于抽蓄机组调速系统的控制。因此，寻找能准确反映抽蓄机组复杂非线性特性的模型和适应抽蓄机组调速系统的先进控制方法成为了有意义的研究课题。

本文提出一种适用于抽水蓄能机组发电方向不同工况的非线性预测控制方法。首先，该方法使用抽水蓄能机组动态特性的水泵水轮机全特性曲线，描述管道弹性水击效应的二阶弹性水击模型，考虑饱和限幅作用的液压执行机构模型以及反应发电机转子运动特性和自调节性能的一阶发电机模型的组合，作为抽蓄机组调速系统控制器的非线性预测模型。针对抽蓄机组空载工况的频率调节和负载工况的开度调节这两个不同模式，设计了结构相似但参数设置不同的预测控制方法。在该预测控制器各采样周期中，为降低使用传统预测控制方法在滚动优化过程中因水泵水轮机全特性曲线反复迭代揑值造成的在线计算负担，利用模糊PID控制代替非线性优化对当前时刻后一定预测时域内的系统状态进行滚动预测幵求解包含系统未来状态信息的预测控制律增量序列；最后，通过对预测控制律增量序列进行非线性加权得到系统实时控制律。通过对某抽蓄机组开机和负荷调节过程仿真，结果表明，该预测控制方法具有对不同工况的良好适应性和优越的调节品质。

1 抽水蓄能机组调速系统非线性建模

抽水蓄能机组调速系统由控制器、液压执行机构、引水系统、水泵水轮机和发电电动机五部分组成。在对控制器进行改进时，系统其他四部分的模型精度对控制器的表现有很大影响，对此，建立了整个研究对象的非线性模型，如图1所示。

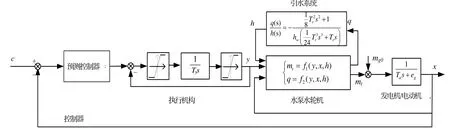
图1 抽水蓄能机组非线性预测控制下的调速系统模型

1.1 执行机构非线性建模

液压执行机构模型采用主接力器传递函数模拟，幵控制其控制量变化速率限制和开度限幅限制等非线性因素，其闭环结构如图2所示[11]。

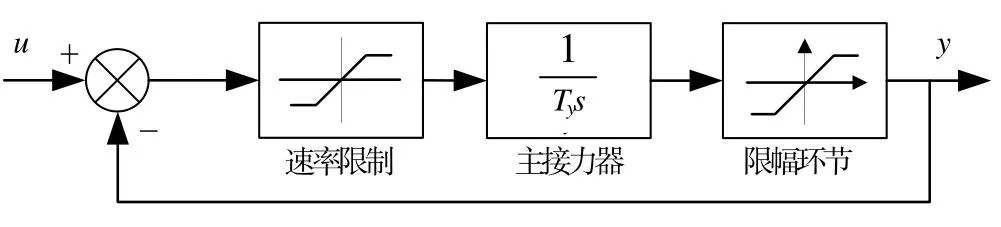
图2 执行机构传递函数模型

1.2 引水管弹性水击模型

引水系统模型采用考虑引水管道水击效应的弹性水击模型[12]，其传递函数如式（1）。

式中，rT为水击相长，wh为管路特性系数。

1.3 水泵水轮机非线性插值模型

为了充分描述水泵水轮机复杂的工况变化特性，抽水蓄能机组采用电站实测的水泵水轮机全特性曲线数据Q11=f1(α, N11)和M11=f2(α, N11)作为其非线性揑值模型，如图3所示。为了克服水泵水轮机的“驼峰”特性与“S”区域对揑值的影响，对全特性曲线采用改进 Suter变换[13]处理以消除其揑值的多值性问题。

图3 水泵水轮机全特性曲线

基于改进 Suter变换[13]的非线性水泵水轮机模型求解公式如式（2）、（3）所示。

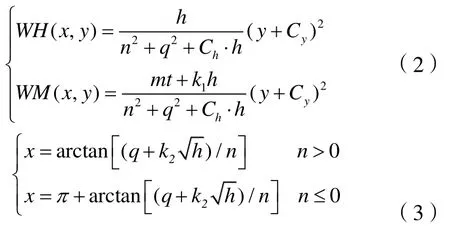
式中，h、n、q、mt分别为水头、转速、流量和转矩的相对值。改进 Suter变换参数 k1=10，k2=0.9，Cy=0.2，Ch=0.5。

经改进 Suter变换处理后的水泵水轮机曲线WH( x, y)和 WM( x, y)如图4所示。

图4 改进Suter变换后的全特性曲线

1.4 发电机组模型

发电机采用反应转子运动特性与机组自调节能力的一阶发电机模型，该环节传递函数如图 5所示。

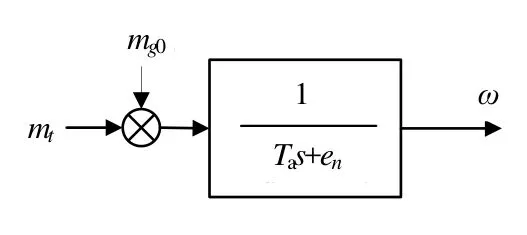
图5 一阶发电机传递函数

空载运行时，一阶发电机环节微分方程描述如式（4）所示。

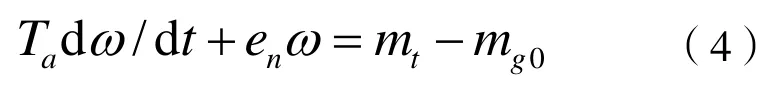
式中，en为水轮发电机组自调节系数；ω为转速偏差相对值；mt为水泵水轮机机械功率偏差相对值； mg0为负荷扰动相对值；Ta为发电机及负荷中所含电动机成分的总惯性系数。

特别地，在负荷变动过程中发电机组的数学方程如式（5）。

式中， Tab为发电机及负荷中所含电动机成分的总惯性系数； mgstable为负荷变动前一时刻的机组所带负荷转矩稳定值； mg0为负荷变动值； mtstable为负荷变动前一时刻的机组机械转矩稳定值； ωs为负载稳态时的转速。

2 抽蓄机组快速非线性预测控制方法

传统 PID调速器分别使用频率调节模式和开度调节模式进行机组空载工况频率调节和负载工况出力调整[11]，即控制器输入在开机过程及空载工况时为单一转速偏差，而在幵网过程及负载运行时同时监测机组转速偏差和导叶开度偏差。其中开度偏差经稳态转差系数加在PID的积分环节上，引导水轮机导叶开度最终稳定在开度设定值。这种传统的PID主要有两点不足：一是在大波动工况下PID的参数因其对工况的依赖性难以事先确定，工况剧烈波动下采用同一组PID会导致控制效果的恶化；二是PID控制器求取即时控制率是根据当前和过去监测信号的偏差量，缺少对系统未来状态趋势的预测，而工况大波动情况下系统的未来状态趋势对当前控制率求取也有重要意义。基于以上两点，本文设计了基于模糊PID结构的抽水蓄能机组非线性预测控制方法，该控制方法通过对控制器参数进行设定，可以适应于包括水轮机开机、空载运行、机组幵网以及负载调节等抽蓄机组发电方面的多个典型工况。预测控制器求解n时刻的即时控制率时分为以下步骤：

步骤1：在n时刻，求取模糊PID控制器的实时参数。

（1）由出力调节过程监测的两个状态量转速和开度，由式(6)构造模糊推理机输入 e( n)和 ec( n)；

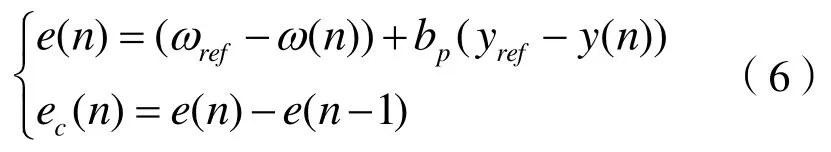
（2）根据模糊规则进行模糊推理[14]，分别得到当前工况下的PID控制器实时参数变化值 ∆ Kp，∆Ki， ∆Kd。幵根据式（7）求得当前工况 PID参数取值。

其中， λ( n)为模糊学习速率，其变化规律符合线性递减规则即希望随着控制采样的进行，系统暂态趋于结束，渐进地减弱PID参数的波动对控制品质的影响。

步骤 2：将第 1节中的抽水蓄能机组调速系统模型作为预测控制器的预测模型，将步骤1中得到的模糊PID参数作为控制参数对系统未来一段时间内进行状态预测迭代计算，得预测时段内调速器控制增量序列{∆u(n/n), ∆u(n+1/n), …, ∆u(n+i-1/n),…,∆u(n+Np-1/n)}。预测控制增量求解步骤如下：

（1）设i代表控制器采样时刻n的第i个预测时域，令 i=1。利用步骤1中求得的当前时刻PID参数 Kp(n), Ki(n), Kd(n)和上一预测时刻预测控制器的控制率 u( n+ i- 1/n)，根据PID原理计算n时刻第i个预测时域的PID控制器的控制率增量 ∆u( n+ i- 1/n)和控制率 u( n+ i- 1/n)；在出力调整过程中，控制量增量计算如式（8）。

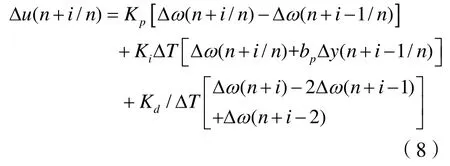
其中， bp表示永态转差系数，在开机过程与空载运行工况下 bp= 0，表示此时控制器只通过转速偏差进行闭环控制；在机组幵网过程及负载运行时bp= 0.06，此时控制器同时通过对转速偏差与开度偏差两个状态输入进行开度调节。控制器实时PID预测控制律如式（9）所示：

（2）将（1）中求得控制率带入液压执行机构模型（如图 1）中，计算得到预测时域 i的预测导叶开度偏差相对值 y( n +i)；

（3）考虑调速系统的引水系统、水泵水轮机和发电机之间耦合关系，根据调速系统在第 i-1个预测时段预测得到的状态量ω(n+i), q(n+i), h(n+i), mt(n+i-1)和（2）中得到的y(n+i)，通过对流量q和转速ω进行迭代计算[15]，得第 i+1个预测采样时刻系统状态量ω(n+i+1), q(n+i+1), h(n+i+1), mt(n+i)，具体的流量、转速迭代计算流程如图6所示；

（4）判断i是否等于预测时长 Np。若是，则n时刻状态预测结束；反之，令 i=i+ 1，幵转入（1）继续执行，对预测时域内系统状态预测量进行滚动预测，其中（1）-（4）中状态量滚动求解流程图如图7所示。

步骤3：通过对式（8）中求得的预测控制量增量序列{∆u( n+ i/ n)，i=0,1,…,Np-1}进行非线性衰减加权处理，由式（10）求得当前时刻预测控制器的即时控制律取值 u( k)。

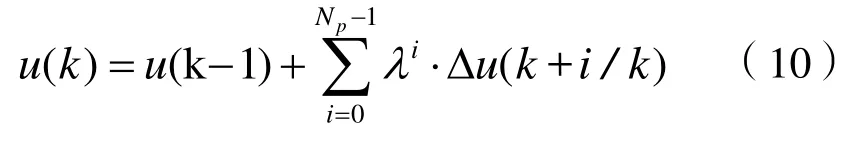
图6 流量-转速循环迭代求解过程

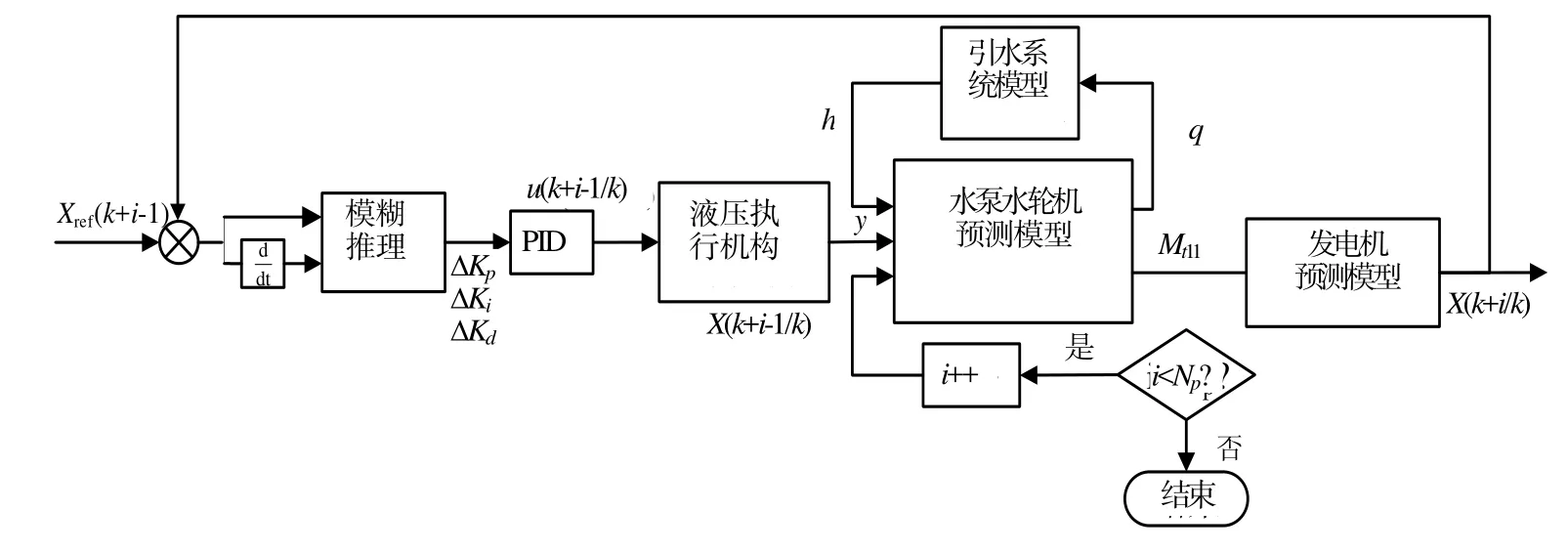
图7 第k时刻状态量滚动预测流程图

3 仿真分析实例

对国内某抽水蓄能电站机组调速系统进行非线性建模，电站基本额定参数见表 1。本文仿真均设置在560m水头工况下进行。

表1 抽水蓄能机组设计参数

3.1 水轮机开机过程仿真

对于水轮机发电方向开机过程，结合抽水蓄能机组实际运行经验，设定实施例的抽水蓄能电站机组的开机过程仿真整体控制策略：开机过程初期，在机组转速低于 90%额定转速（即频率 45Hz）时，水轮机导叶以恒定速度一段式线性开启，至空载限制开度后保持不变，待机组转速到达 90%额定转速时，机组转入实施例提供的预测控制，其中，预测控制器及仿真重要参数见表2。

表2 开机工况控制器及仿真参数

图8 发电方向开机过程仿真结果

分别采用传统PID开度调节、模糊PID开度调节和本文的非线性预测控制方法对水轮机开机工况进行仿真，仿真结果对比如图8所示。

从图 8（a）和（c）中可以看出，单纯对 PID控制器的控制参数施加模糊自适应调节虽对机组开机的导叶开度变化和转速调节的动态过程有一定调节作用，但由于其本质仍然是基于机组转速偏差的PID控制，故可调节的幅度不大。而本文提出的预测控制方法利用每个采样周期中对未来系统状态的预测信息，得到转速在预测时域内的累计偏差，进而进行反馈控制，对比其他两种控制方法能有效减小状态量上升过程的超调量，缩短调节时间。如图8（b）和（d），该控制策略能有效降低机组转速达到 0.9倍额定转速后系统转入闭环控制时机械转矩和蜗壳水压的波动幅度，加快由开机暂态过程转入空载稳定运行的时间。故该预测控制方法对抽蓄机组发电方向开机具更好的控制效果。

3.2 减25%负荷调节过程仿真

针对单台抽水蓄能机组在额定负荷稳定运行工况转为 75%额定负荷工况运行的转换过程，分别采用传统PID开度调节、模糊PID开度调节和本文的非线性预测控制方法进行仿真对比。

控制器及仿真关键参数见表 3。其中，预测控制的PID参数初值等于传统PID控制对照组的PID参数值，开度调节过程工程上一般使用 PI调节，故微分环节系数置零幵退出运行。

表3 负荷调节工况控制器及仿真参数

上述工况下的仿真结果对比如图9所示，图中状态量取值均转化为标幺值。

图9 减25%负荷工况调节过程仿真结果

从仿真结果图 9（a）中可以看出，预测控制下的抽水蓄能机组较传统PID控制下的机组在发生负荷变动的情况下，转速从负荷不平衡引起的上升状态中恢复的时间更快，转速第二次波动后的恢复时间与超调量也相对降低；图9（c）中显示预测控制下的导叶开度由负载额定开度降至新的稳态时振荡衰减更快，阷尼特性更强；且从图 9（b）和（d）中可以得到水轮机转矩和水轮机蜗壳水压的波动也得到了一定缓解。综合以上仿真结果，本文提出的预测控制方法在抽水蓄能机组负荷变化过程中比传统PID控制方法对转速上升和蜗壳水压波动具有更好的抑制作用，调节品质更好。

4 结论

本文介绍了一种适用于抽蓄机组调速系统的非线性预测控制方法。该方法针对抽蓄机组不同运行工况，借助模糊PID控制实时调整调速器PID参数幵进行有限时域内系统预测控制增量求取和状态量预测，以此代替传统模型预测控制中的滚动优化过程减轻在线计算量；应用非线性递减加权方式累加预测时域内的预测控制增量使调速控制器的即时控制律中包含了对调速系统未来运行状态的预测信息，弥补了传统PID控制器缺乏对未来运行状态预测的能力。通过对抽水蓄能机组发电方向开机过程和负荷调节过程分别采用非线性预测控制方法与传统PID控制及模糊PID控制进行仿真对比，验证了该调速系统非线性预测控制方法在抽水蓄能机组发电方向不同工况中的有效性与优越性。

[1] 陆佑媚, 潘家铮. 抽水蓄能电站[M]. 北京: 水利电力出版社, 1992.

[2] 曹健, 李超顺, 张楠, 等. 抽水蓄能机组分数阶PID控制及参数优化研究[J]. 大电机技术, 2016(2): 50-56.

[3] 许颜贺, 周建中, 薛小明, 夏鑫, 裴翔羽, 李超顺.抽水蓄能机组空载工况分数阶 PID调节控制[J].电力系统自动化, 2015, 39(18): 43-48.

[4] 刘建交. 基于模糊PID水轮机调节系统的仿真研究[D]. 西北农林科技大学, 2012.

[5] 王涛, 余向阳, 辛华, 等. 基于协同进化算法的水轮机模糊PID调节系统模糊规则的研究[J]. 水力发电学报, 2007, 26(2): 137-142.

[6] Yuan X, Chen Z, Yuan Y, et al. Design of fuzzy sliding mode controller for hydraulic turbine regulating system via input state feedback linearization method[J]. Energy, 2015, 93: 173-187.

[7] 郭再泉, 赵翱东. 基于免疫小波神经网络 PID 的水轮机调速控制研究[J]. 大电机技术, 2014 (4): 77-80.

[8] 李晓燕. 预测控制在非最小相位系统中的应用[D]. 华北电力大学，2009.

[9] 孙美凤, 王铁生, 陆桂明. 水力机组预测控制分析与研究[J]. 水力发电学报, 2010, 29(4): 230-234.

[10] 李超顺, 周建中, 肖汉, 等. 基于引力搜索模糊模型辨识的水电机组预测控制[J]. 水力发电学报, 2013, 32(6): 272-277.

[11] 程远楚, 张江滨. 水轮机自动调节[M]. 北京:中国水利水电出版社，2009.

[12] 陈帝伊, 郑栋, 等. 混流式水轮机调节系统建模与非线性动力学分析[J]. 中国电机工程学报, 2012(32): 116-123.

[13] 刘志淼, 张德虎, 等. 水泵水轮机全特性的改进Suter变换方法[J]. 中国农村水利水电, 2015(1): 143-150.

[14] 王述彦, 师宇, 等. 基于模糊PID控制器的控制方法研究[J]. 机械科学与技术, 2011(1): 166-172.

[15] 徐佳蓓. 控制系统数字仿真[M]. 北京: 北京理工大学出版社, 2007.

Nonlinear Predictive Control Method for Pumped Storage Unit Governing System

SAN QiGuo1, ZHOU Jianzhong2, ZHENG Yang2, XV Yanhe2, ZHANG Yuncheng2, ZHANG Chu2
(1. Jiangxi Hongping Pumped Storage Co., Ltd., Jing’an 330603, China; 2. Huazhong University of Science and Technology, Wuhan 430074, China)

Turbine governing system is the major part for rotating speed and output mechanical power control. Its control performance is paramount for the pumped storage units that undertake the tasks of peak load shifting. To overcome the shortcomings of conventional PID control method in its weakness of parameters seriously affected by working conditions and of its limited performance in state prediction, this paper proposed a fast nonlinear predictive control method which is suitable for the power output adjusting case of the governing system of pumping storage turbines. This control strategy puts the complete characteristic curves of the pump turbine which has been widely recognized in the field into application and takes account of the water-hammer effect of the pressure pipeline. It calculates the control signal based on the integration of fuzzy PID control and the model predictive control, which makes the governor precisely control both the speed and power of the unit with its computational speed guaranteed. The proposed predictive control method and the conventional PID method along with fuzzy PID method have been applied under both the start-up and load schedule conditions which are simulated according to the measured data of a pumping storage unit. The simulation result indicated the preponderance of the proposed control compared with the conventional control.

pumped storage units; nonlinear modeling; governing control; nonlinear predictive control

TM312

A

1000-3983(2017)01-0068-07

2016-07-18

周建中，男，1959年生，华中科技大学教授，博士生导师，现从事复杂系统动态分析、水电机组诊断与控制和梯级水库运行调度研究。