网络空间中线要素的核密度估计方法
2017-02-16唐炉亮阚子涵刘汇慧吴华意
唐炉亮,阚子涵,刘汇慧,2,孙 飞,吴华意
1. 武汉大学测绘遥感信息工程国家重点实验室,湖北 武汉 430079; 2. 武汉大学测绘学院,湖北 武汉 430079
网络空间中线要素的核密度估计方法
唐炉亮1,阚子涵1,刘汇慧1,2,孙 飞1,吴华意1
1. 武汉大学测绘遥感信息工程国家重点实验室,湖北 武汉 430079; 2. 武汉大学测绘学院,湖北 武汉 430079
核密度估计(KDE)方法是分析点要素或线要素空间分布模式的一种重要方法,但目前线要素核密度方法只能分析线要素在二维均质平面空间的密度分布,不能正确分析交通拥堵、交叉口排队、出租车载客等线事件在一维非均质道路网络空间中的密度分布。本文提出了一种网络空间中线要素的核密度估计方法(网络线要素KDE方法),首先确定每个线要素在网络空间上的密度分布,然后根据网络空间距离和拓扑关系确定网络空间的线要素核密度与时空分布。以出租车GPS轨迹数据中提取的“上客”线事件为例,分析出租车“上客”线事件在网络空间中的密度分布,通过与现有方法比较的试验结果表明,本文提出的方法更能准确反映路网空间中线事件的分布特征。
线事件;网络空间;核密度;时空GPS轨迹
在道路网络空间中,有一类具有起止点和发生过程的事件或现象,通常称为线事件,如交通拥堵、交叉口排队等候、出租车载客等,这些线事件的发生和分布受道路网络的空间格局与拓扑关系的影响,在道路网络中呈现连续线状分布。现有线要素分布模式分析方法只能分析线要素在二维延展均质平面空间的密度分布,不能正确分析线要素在非均质道路网络空间中的密度分布,因此研究一种非均质网络空间中线要素分布模式分析方法具有重要意义。
核密度估计(kernel density estimation,KDE)是分析空间要素聚集效应的一种重要的非参数化方法[1-2],通过将整个研究区域生成一个光滑的密度表面来分析点事件的空间聚集特征,找出事件的高发区域,在经济、人口统计以及影像分类处理等方面都有广泛应用[3-8]。典型的KDE方法基于各向同性的二维均质空间,但对于发生和分布受一维网络格局限制的事件来说,各向同性的假设就过于牵强[9]。网络KDE方法以网络距离代替欧氏距离[4-5,10-13],如文献[4—5]根据网络距离得到一个多边形搜索区域,代替整个均质平面;文献[10]以路网线性单元为密度估计的基本单位,得到整个路网的核密度分布;文献[11]提出非连续和连续等分核函数法两种网络的核密度估计模型,并验证了交叉口处的无偏性;文献[12]将文献[4—5]的方法和文献[10]提出的方法进行了比较;文献[13]提出了网络KDE方法的一般形式,分析了城市路网中设施POI分布特征。
目前线要素的分布模式分析方法仍然有所欠缺。已有线要素分析方法主要将线要素空间分布转化为点要素空间分布[14-15]、采用平面线要素KDE方法估计道路网密度分布[16-17]或利用三维空间的KDE方法估计时空轨迹的密度分布[18-19]。通过分析可知,目前线要素密度分布分析方法都以均质空间为基础,没有考虑交通拥堵、交叉口排队、出租车载客等线事件受路网格局和网络方向的限制而呈现的分布特征。本文提出一种网络空间的线要素核密度估计方法,以网络距离为度量,顾及网络拓扑方向,分析线事件在网络空间中的分布特征和分布模式。
1 网络空间中线要素的核密度估计方法
网络空间中线要素的核密度估计方法(网络线要素KDE方法),首先定义交通拥堵、交叉口排队、出租车载客等线事件,并在平面线要素KDE方法的基础上,进行以下两个方面的改进和拓展。
(1) 在核密度延展方向和衰减效应方面,将平面线要素KDE方法中线要素核密度“均质二维方向延展”和“平面距离衰减效应”改进和拓展为“非均质网络方向延展”和“网络距离衰减效应”。
(2) 在线要素密度计算方面,考虑线要素的起止方向和网络方向及拓扑连通性,考虑网络节点处密度计算的特殊情况,保证节点密度估计的无偏性。
1.1 线事件的定义及表达
在网络空间中,具有起止点并呈线状连续分布的事件称为线事件(linear event,LE),可表达为
LE={ID,S,E,L,TS,TE}
式中,ID为线事件LE的编号;S、E分别为LE发生的起止位置点;L为起止点间发生和分布的网络空间,数学表达为路网N的子集:L∈N;TS和TE分别为线事件起止时间点,网络空间中的线事件表达如图1所示。

图1 路网中线事件的表达Fig.1 Representation of linear events in road network
1.2 单个线要素在网络空间中的密度分布
平面线要素KDE和网络线要素KDE均以标准点要素平面 KDE方法为基础,通过为每个点生成一个光滑的密度表面来估计整个平面的密度值,如图2所示。

图2 标准点平面要素KDEFig.2 Standard planar KDE for point features
图2中,函数f(x)为单个点要素i在均质平面中的密度分布函数;r为距离阈值。在r范围内,随着与点要素i距离的增加,对应的密度值f(x)减小,与i距离大于等于r的位置处f(x)等于零,即通过考虑“距离衰减效应”确定每个点要素的密度分布。f(x)的值由式(1)确定
(1)
式中,si为点要素i所在位置;x-si为位置x与i的欧氏距离;k为距离衰减函数,也称为核函数。k的形式有多种,如高斯函数、二次多项式函数、四次多项式函数等。
与平面点要素KDE类似,平面线要素KDE在阈值r的范围内在线要素上方覆盖一个核表面,表示线要素密度影响的各向同性“距离衰减效应”,如图3(a)所示。而与平面线要素KDE的各向同性性质不同,网络空间中线要素的密度分布受网络空间格局和网络方向的约束,其影响范围限制在非均质网络空间内,所以网络线要素KDE方法将以往的平面欧氏距离改进和拓展为网络距离,在阈值r范围内按照网络空间中的“网络距离衰减效应”在每个线要素上方覆盖一条平滑曲线,即核曲线f(x),表示单个线要素在网络空间中的密度分布,如图3(b)所示。

图3 网络线要素KDE核曲线与平面线要素KDE核表面Fig.3 Kernel surface in planar KDE and kernel curve in network KDE
线要素在网络空间中的密度分布函数f(x)由点要素推导而来。由于线要素l可以看作由起点S和终点E之间无限个连续分布的点要素组成,因此网络空间中单个线要素的密度分布应为线要素上所有点的密度分布在网络空间中的矢量和。在线要素影响域r范围内,网络线要素的密度值f(x)在数学上应表示为从线要素起点S至终点E,连续移动核函数在线要素上的积分,即核函数与线要素围成的面积。如图4所示,阴影部分面积即分别为位置S、O、E处的密度f(S)、f(O)、f(E)。可以看出,在线要素外距离线要素端点大于等于r的位置线密度为零,越接近线要素中心的位置,密度越大,在线要素内且与端点网络距离大于等于r的位置处阴影部分面积充满整个核函数,密度达到最大,之后将保持不变,以此得到线要素核密度分布曲线为图4中红色曲线。因此对于单个线要素l来说,其在网络空间中的密度分布曲线f(x)为
(2)
本文选择二次多项式函数作为核函数,如式(3)所示
(3)

图4 网络空间线要素核密度分布Fig.4 Kernel density distribution for linear feature in network space
1.3 顾及网络拓扑关系的线事件密度分布
现有道路网络中事件的空间分布研究均将道路视作单线且双向连通[4-5,10-11],然而一方面由于路网的复杂性和线事件本身具有的起止方向性,另一方面事件的发生机制受交通流的影响,即使同一条道路的不同方向上事件分布模式并不相同,因此在计算网络空间线密度分布时,需要顾及路网拓扑方向的约束。
1.3.1 网络空间弧段上的密度分布
线事件在网络空间弧段上的密度分布顾及网络拓扑关系,以网络距离r作为距离衰减阈值,得到阈值范围内的线要素。图5中的灰色区域分别为平面线要素KDE方法和网络线要素KDE方法得到的阈值范围,网络线要素KDE对网络距离与拓扑关系的考虑体现在两个方面,一是通过网络距离得到网络阈值范围,而非平面线要素KDE方法得到的各向同性圆形阈值范围;二是顾及了局部网络的可达性及线事件的方向性,例如线要素3的方向与估计点X所在道路方向相反,对X处密度影响应为零,而在平面线要素KDE中,圆形范围内的线要素则都要考虑。
在得到范围r内的线要素之后,网络空间中线要素密度估计结果应该是每个线要素密度分布曲线值在路网中的叠加。对网络空间弧段上每点进行密度估计时,考虑范围r内所有线要素,得到的空间位置x处的线密度应为
(4)
式中,li为x阈值范围内的线要素;n为阈值范围内线要素总个数。

图5 平面线要素KDE和网络线要素KDEFig.5 Planar KDE and network KDE for linear feature
1.3.2 网络空间节点处的线事件密度估计
节点是网络拓扑性质改变的位置,节点处由于边数增多,考虑范围会增大,无论是平面线要素KDE方法还是普通的网络KDE方法均无法保证节点处密度估计的正确性。本文按照文献[11]提出的点要素等分核函数方法实现节点处线要素密度估计的无偏性。等分核函数计算原理如图6所示,节点I的度为4,对于待估计的位置,与X同一边的核函数形式保持不变,X邻接边核函数k减小为原来的1/3;若X的阈值范围r内包括多个节点,设每个节点的度ni,则X网络节点下行方向上的每条边核函数依次减少为上一边核函数的1/(ni-1),这使无论空间位置X附近是否存在节点,X处密度最大值为核函数在整个阈值范围r内的积分,从而保证X密度的最大值不变,避免了密度值的过度估计,保证交叉口处线密度估计的真实性。核函数k(s-x/r)的形式如式(5)所示
(5)
最后,结合式(3)—式(5),即可得到路网空间中的线要素密度分布。
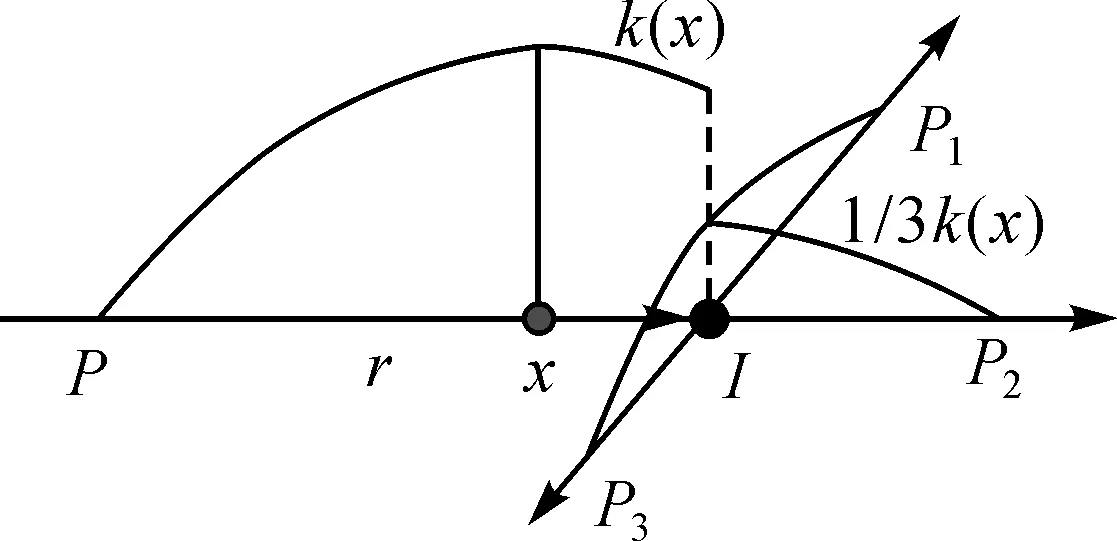
图6 节点处核密度估计Fig.6 Kernel density estimation at nodes
1.4 网络空间线要素核密度估计模型算法实现
网络空间线要素核密度的算法实现如图7所示,主要分为3个部分:网络分割、线要素处理和密度计算。将网络在节点处断开,得到一系列网络弧段,将弧段按照一定长度等分成基本线性单元(basic segment unit,BSU),构建以BSU为基本单位的拓扑结构。将网络中的线要素起止点分配到最近的BSU端点上,此时每个线要素视作经过整数个BSU,记录每个BSU上经过的线要素个数。确定距离阈值r,依次计算网络中每个BSU的密度,计算方法为:首先根据网络距离r确定阈值范围内的BSU,然后将每个BSU上的线要素个数作为数乘因子(没有线要素经过则为0),在网络距离阈值范围内计算每个BSU的密度权重,最后累加阈值范围内所有BSU的密度权重得到待估计BSU的密度值。

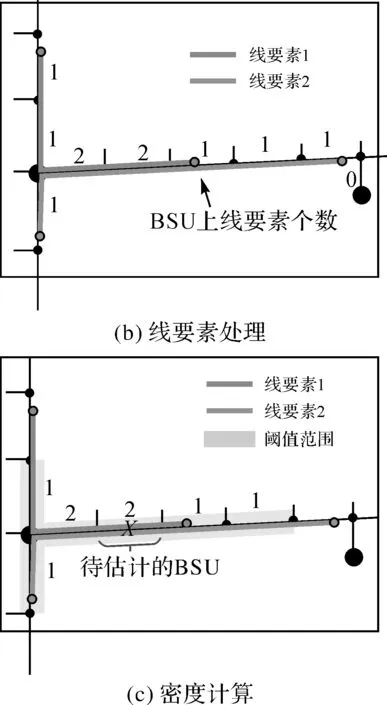
图7 网络线要素KDE算法实现Fig.7 Algorithm and implementation of KDE for network linear feature
密度计算如式(6)所示
(6)

2 试 验
本文以Microsoft Visual C# 2010为开发语言,采用ESRI ArcGIS 10.1对线要素核密度计算结果进行可视化,选取武汉市路网和浮动车数据为研究对象,该数据按照40 s等时间间隔采集,包含出租车ID、经度、纬度、速度、方向、载客状态(满载为“1”,空载为“0”)。本文针对出租车“上客”事件抽取出相邻两条载客状态分别为“0”和“1” 的数据,由于出租车GPS轨迹采集具有时间间隔,相邻载客状态分别为“0”和“1”的记录所对应的位置只能代表数据采集瞬间出租车的载客状态,只能确定“上客”事件发生在0→1之间,无法获知其具体发生的时间和地点,因此“上客”事件成为有起点和终点的“上客”线事件,本文提取相邻状态分别为0和1的“上客”事件共278个,其分布如图8所示。
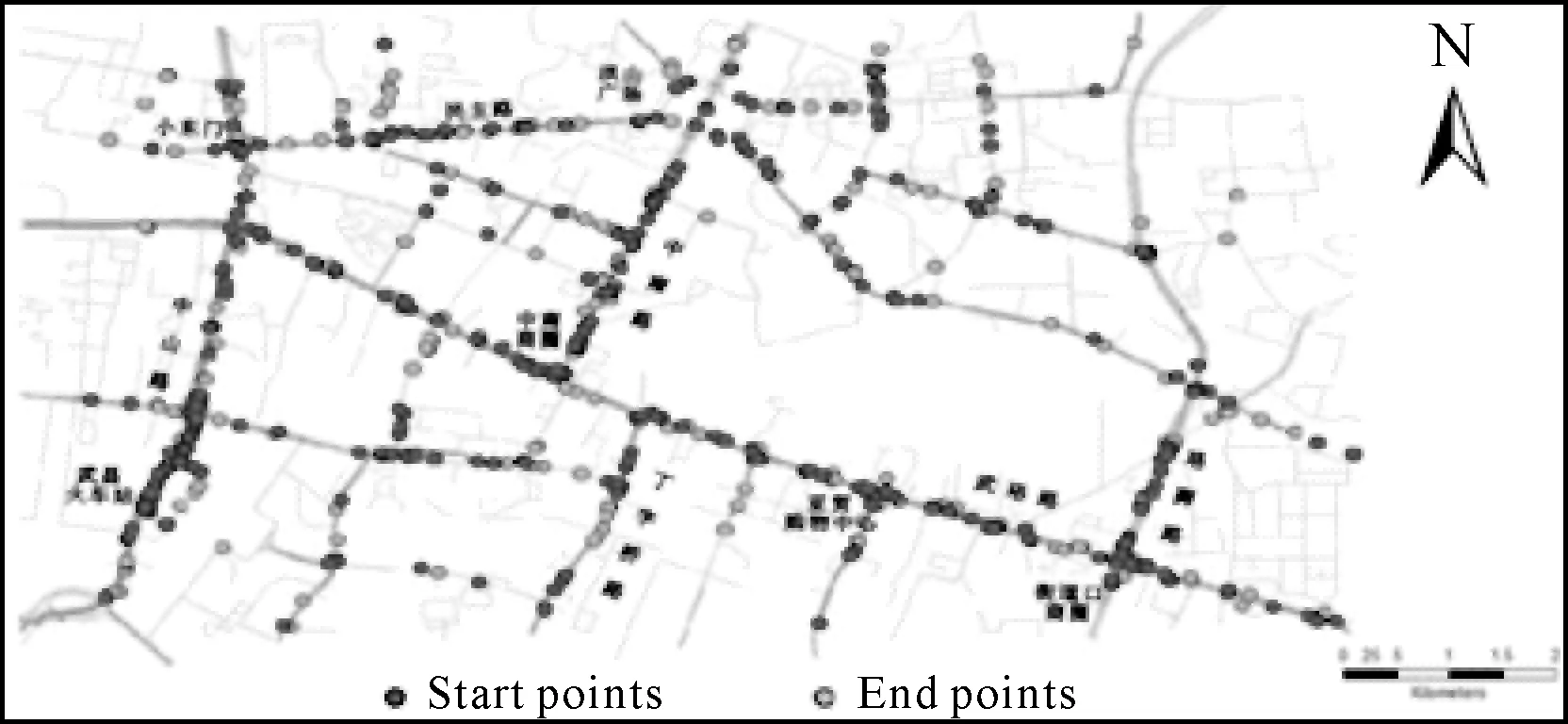
图8 试验区域路网和“上客”线事件起止点分布Fig.8 Road network in experiment region and distribution of start and end point of “pick-up” linear events
试验中以20 m BSU长度对路网进行分割,统计“上客”线事件在每个BSU上的分布,并以100 m为距离衰减阈值,采用本文提出的顾及网络空间距离和拓扑关系的线要素核密度分析方法对该“上客”线事件数据进行密度计算和分布模式分析,并将结果与样方法(20 m样方大小)和平面线要素KDE方法(20 m×20 m栅格大小,100 m阈值)进行比较,按照本文方法处理“上客”线事件密度分布结果如图9(a)所示,样方法处理的“上客”线事件密度分布结果如图9(b)所示,平面线要素KDE方法处理的“上客”线事件密度分布结果如图9(c)所示,处理结果的局部放大效果如图10所示。
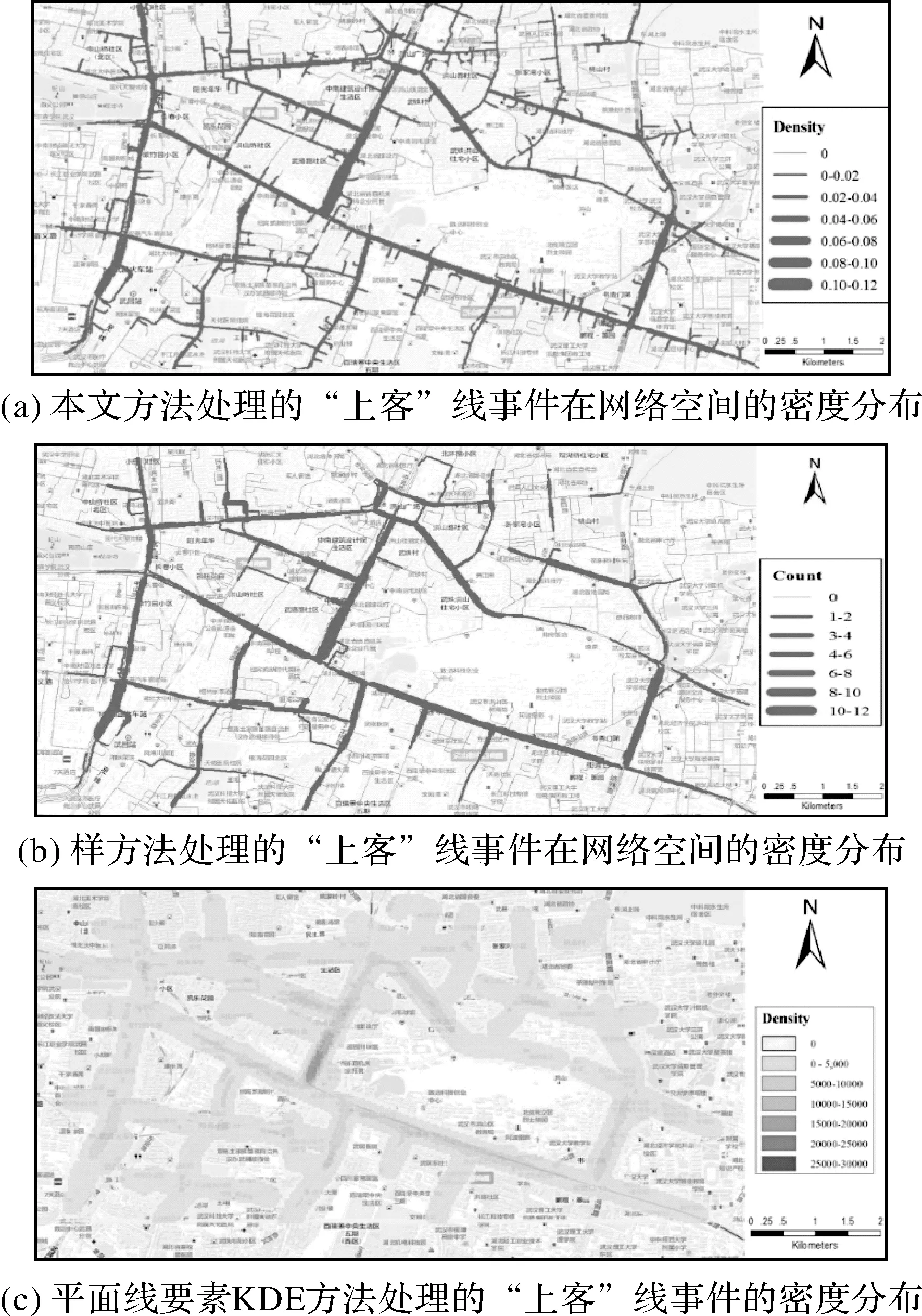
图9 不同处理方法的“上客”线事件在网络空间的密度分布Fig.9 Density distribution of “pick-up” linear events in network space processed by different methods
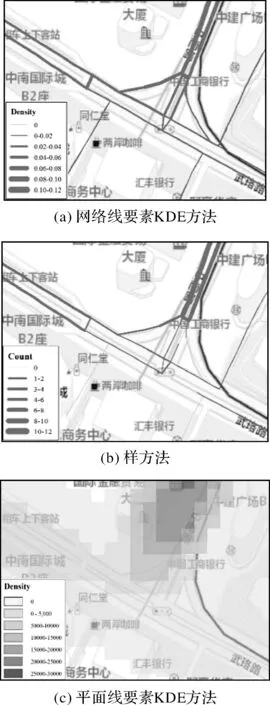
图10 局部范围3种方法的比较Fig.10 Comparison of the three methods for linear features in a local scale
从图9可以看出,本文提出的网络线要素KDE方法和样方法、平面线要素KDE方法都能在一定程度上反映出线事件的网络空间分布特征,“上客”事件发生密集分布于珞狮路、武珞路中部、中南路南部、中山路南部。这些道路上有街道口商圈、中南路商圈等经济热点地带,以及轨道交通地铁2号线站点、武昌火车站等交通热点地带,这些位置对于出租车的需求较大,因此是“上客”事件的高发点。通过对图9、图10的分析可以看出,本文提出的网络线要素KDE方法处理的“上客”线事件将密度分布限制于城市道路网络空间内,更加符合“上客”事件本身发生和影响在道路网络上,而非覆盖在道路网络外的事实。本文方法处理的“上客”线事件的密度在同一道路上分布很连续,在不同等级道路上分布较均衡,密度分布具有差异性但不存在突变情况,可以如实地反映“上客”线事件在路网中分布特征, 并且能更好地体现细节信息,如图9(a)、图10(a)所示。图9(b)、图10(b)为样方法处理的“上客”线事件密度分布结果,图中出现密度在一条道路中间突然断开、分布不连续的情况,这表示“上客”线事件在这一位置发生的概率有突变,即这一位置不可能有“上客”线事件的发生,这显然不符合事实。图9(c)和图10(c)中的平面线要素KDE方法由于计算整个平面的线密度分布,以二维欧氏距离度量事件的发生和影响范围,没有考虑路网空间的非均质空间特性,使“上客”线事件的影响范围向道路空间外延展,因此处理结果中“上客”线事件的核密度存在于二维延展的均质空间,覆盖于城市道路网络之外,不符合“上客”线事件发生在道路范围内的事实。
3 结 论
鉴于现有的点模式分析方法和线要素核密度方法只能分析线要素在二维延展均质平面空间的密度分布,不能正确分析交通拥堵、交叉口排队、出租车载客等线事件在非均质道路网络空间中的密度分布,本文提出一种网络线要素KDE方法,该方法首先确定线要素在网络空间的密度分布,然后根据网络空间距离和拓扑关系确定网络空间中线要素密度分布,并以出租车GPS轨迹数据中提取出的“上客”线事件为例,分析了出租车“上客”线事件在网络空间中的线密度分布。试验结果表明,本文方法处理的“上客”线事件的密度在同一道路上分布连续,在不同等级道路上分布较均衡,密度分布具有差异性但不存在突变情况,能更好地体现细节信息,通过与现有方法的比较认为,本文提出的方法更能准确地反映路网空间中线事件的分布特征。在提高算法效率、计算线要素的密度衰减效应时应考虑道路等级、并对交通流特性作定量分析。作者将对此作进一步研究和完善。
[1] SILVERMAN B W. Density Estimation for Statistics and Data Analysis[M]. New York: Chapman & Hall, 1986.
[2] BAILEY T C, GATRELL A C. Interactive Spatial Data Analysis[M]. Harlow Essex, England: Longman, 1995.
[3] TIMOTHÉE P, NICOLAS L B, EMANUELE S, et al. A Network Based Kernel Density Estimator Applied to Barcelona Economic Activities[C]∥Proceedings of International Conference on Computational Science and Its Applications-ICCSA 2010. Berlin Heidelberg: Springer, 2010: 32-45.
[4] BORRUSO G. Network Density Estimation: A GIS Approach for Analyzing Point Patterns in Network Space[J]. Transactions in GIS, 2008, 12(3): 377-402.
[5] BORRUSO G. Network Density Estimation: Analysis of Point Patterns over a Network[C]∥Proceedings of International Conference on Computational Science and Its Applications-ICCSA 2005. Berlin Heidelberg: Springer, 2005: 126-132.
[6] 吕安民, 李成名, 林宗坚, 等. 人口密度的空间连续分布模型[J]. 测绘学报, 2003, 32(4): 344-348. LÜ Anmin, LI Chengming, LIN Zongjian, et al. Spatial Continuous Surface Model of Population Density[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(4): 344-348.
[7] 杨红磊, 彭军还. 基于马尔可夫随机场的模糊c-均值遥感影像分类[J]. 测绘学报, 2012, 41(2): 213-218. YANG Honglei, PENG Junhuan. Remote Sensing Classification Based on Markov Random Field and Fuzzy c-means Clustering[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 213-218.
[8] 周恩策, 刘纯平, 张玲燕, 等. 基于时间窗的自适应核密度估计运动检测方法[J]. 通信学报, 2011, 32(3): 106-114, 124. ZHOU Ence, LIU Chunping, ZHANG Lingyan, et al. Foreground Object Detection Based on Time Information Window Adaptive Kernel Density Estimation[J]. Journal of Communications, 2011, 32(3): 106-114, 124.
[9] MILLER H J. Potential Contributions of Spatial Analysis to Geographic Information Systems for Transportation (GIS-T)[J]. Geographical Analysis, 1999, 31(4): 373-399.
[10] XIE Zhixiao, YAN Jun. Kernel Density Estimation of Traffic Accidents in a Network Space[J]. Computers, Environment and Urban Systems, 2008, 32(5): 396-406.
[11] OKABE A, SATOH T, SUGIHARA K. A Kernel Density Estimation Method for Networks,Its Computational Method and a GIS-based Tool[J]. International Journal of Geographical Information Science, 2009, 23(1): 7-32.
[12] LI Qingquan, ZHANG Tong, WANG Handong, et al. Dynamic Accessibility Mapping Using Floating Car Data: A Network-constrained Density Estimation Approach[J]. Journal of Transport Geography, 2011, 19(3): 379-393.
[13] 禹文豪, 艾廷华. 核密度估计法支持下的网络空间POI点可视化与分析[J]. 测绘学报, 2015, 44(1): 82-90. DOI: 10.11947/j.AGCS.2015.20130538. YU Wenhao, AI Tinghua. The Visualization and Analysis of POI Features under Network Space Supported by Kernel Density Estimation[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(1): 82-90. DOI: 10.11947/j.AGCS.2015.20130538.
[14] BORRUSO G. Network Density and the Delimitation of Urban Areas[J]. Transactions in GIS, 2003, 7(2): 177-191.
[15] WORTON B J. Kernel Methods for Estimating the Utilization Distribution in Home-range Studies[J]. Ecology, 1989, 70(1): 164-168.
[16] CAI Xuejiao, WU Zhifeng, CHENG Jiong. Using Kernel Density Estimation to Assess the Spatial Pattern of Road Density and Its Impact on Landscape Fragmentation[J]. International Journal of Geographical Information Science, 2013, 27(2): 222-230.
[17] YING Lingxiao, SHEN Zehao, CHEN Jiding, et al. Spatiotemporal Patterns of Road Network and Road Development Priority in Three Parallel Rivers Region in Yunnan, China: An Evaluation Based on Modified Kernel Distance Estimate[J]. Chinese Geographical Science, 2014, 24(1): 39-49.
[18] SCHEEPENS R, WILLEMS N, VAN DE WETERING H, et al.Composite Density Maps for Multivariate Trajectories[J]. IEEE Transactions on Visualization and Computer Graphics, 2011, 17(12): 2518-2527.
[19] LEE D, HAHN M. A Study on Density Map Based Crash Analysis[C]∥Proceedings of 2014 International Conference on Information Science and Applications (ICISA). Seoul, South Korea: IEEE, 2014: 1-3.
(责任编辑:宋启凡)
A Kernel Density Estimation Method for Linear Features in Network Space
TANG Luliang1, KAN Zihan1, LIU Huihui1,2, SUN Fei1, WU Huayi1
1. Department of State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China; 2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China
Kernel density estimation(KDE) is an important method for analyzing spatial distributions of point features or linear features. So far the KDE methods for linear features analyze the features’ spatial distributions by producing a smooth density surface over 2D homogeneous planar space, However, the planar KDE methods are not suited for analyzing the distribution characteristics of certain kinds of linear events, such as traffic jams, queue at intersections and taxi carrying passenger events, which usually occur in inhomogeneous 1D network space. This article presents a KDE method for linear features in network space, which first confirms the density distribution of each single linear feature, then computes the density distributions of all linear features in terms of distance and topology relationship in network space. This article extracts “pick-up” linear events from taxi GPS trajectory data and analyzes their distribution patterns in network space. By comparison with existing methods, experiment results show that the proposed method is able to represent the distribution patterns of linear events in network space more accurately.
linear events; network space; kernel density estimation(KDE); spatial-temporal GPS trajectory
The National Natural Science Foundation of China (Nos. 41671442;41571430;41271442)
TANG Luliang(1973—),male, professor,PhD, PhD supervisor, majors in space-time GIS, trajectory data analyzing and mining.
KAN Zihan
唐炉亮,阚子涵,刘汇慧,等.网络空间中线要素的核密度估计方法[J].测绘学报,2017,46(1):107-113.
10.11947/j.AGCS.2017.20150158. TANG Luliang, KAN Zihan, LIU Huihui,et al.A Kernel Density Estimation Method for Linear Features in Network Space[J]. Acta Geodaetica et Cartographica Sinica,2017,46(1):107-113. DOI:10.11947/j.AGCS.2017.20150158.
P208
A
1001-1595(2017)01-0107-07
国家自然科学基金(41671442;41571430;41271442)
2015-03-25
唐炉亮(1973—),男,教授,博士,博士生导师,研究方向为时空GIS、轨迹大数据分析与挖掘。
E-mail: tll@whu.edu.cn
阚子涵
E-mail: kzh@whu.edu.cn
修回日期: 2016-10-08
