基于最大熵-Copula方法的降雨潮位关联性分析——以广州为例

黄锦林，范嘉炜，唐造造

(1.广东省水利水电科学研究院，广东 广州 510635；2.河口水利技术国家地方联合工程实验室，广东 广州 510635；3.天津大学 建筑工程学院，天津 300072)

基于最大熵-Copula方法的降雨潮位关联性分析
——以广州为例

黄锦林1，2，范嘉炜3，唐造造1，2

(1.广东省水利水电科学研究院，广东 广州 510635；2.河口水利技术国家地方联合工程实验室，广东 广州 510635；3.天津大学 建筑工程学院，天津 300072)

强降雨和外江潮位高度直接影响着广州城区受洪涝灾害的程度，对降雨和潮位进行关联性分析，可以为广州市内涝防治提供科学依据。该文构建了年最大潮位和相应1 h降雨量与年最大1 h降雨量和相应潮位关联性分析模型，采用最大熵-AMH Copula方法分别对雨潮组合的治涝风险概率、同现风险概率、组合风险概率、遭遇风险概率进行了比较分析。结果表明：治涝风险概率随两变量重现期的减小而增大；两种组合下的同现分布概率均远小于单变量设计频率；年最大1 h降雨量与相应潮位的相关关系较年最高潮位与相应1 h降雨量的相关关系更弱；在实际工程设计中，适当提高降雨(潮位)设计值可有效降低治涝、遭遇和组合风险概率值。

最大熵；Copula函数；雨潮组合；洪涝灾害；关联性；概率；广州

近年来，随着我国的城市化进程加快和强降雨事件频发，城市发生极端洪涝事件的概率大大增加。由于我国目前城市建筑设施还不健全，排水能力建设相对滞后，防洪能力不足，极易导致内涝灾害的发生，给城市居民的日常生活带来影响，并造成严重的财产损失[1]。对于大多数坐落于江河湖海之滨的城市而言，强降雨给城区造成的受灾程度不仅与降雨量有关，且受外江洪水长期高水位顶托、潮位涨落影响较大。

珠江三角洲地区是国内暴雨日数最多的地区之一，受高速发展的城市化进程和气候变化的影响，珠三角城市暴雨呈上升趋势。广州市位于珠江三角洲北端，属亚热带海洋季风气候，高强度的局部暴雨经常发生，洪涝灾害频繁，对于沿江区域而言，遭遇外江潮水顶托会加剧城市内涝状况，洪水难以外排，造成更加严重的洪涝灾害[2-3]。陈刚[4]通过对近年来广州水雨情数据研究发现集中的超标暴雨是造成广州城区内涝的主要因素；张维[5]指出短历时、高强度的降雨是造成广州城区内涝问题的原因但不是唯一因素，长时间的潮位顶托也是造成严重洪涝灾害的原因之一。因此，考虑短期降雨量和潮位相关联的遭遇风险研究对于广州市内涝防治具有重要意义。

目前，在边缘分布函数的参数估计方面，肖可以[6]等应用最大熵原理研究水文频率分布参数估计和参数优选，为陕北地区水利规划和工程建设提供了科学依据；张明等[7]从梅林变换出发，对多种水文频率分布参数估计的最大熵法进行了推导；陶山山[8]推导了二维最大熵分布函数以及参数的矩估计，并利用多种Copula函数构造二维及多维最大熵模型；童心[9]应用最大熵原理推求了两变量的联合分布，并检验了模型的有效性和优越性。国内外对于多变量的关联性分析多采用Copula构建联合分布函数，即通过对边缘分布函数的拟合来构造变量间的联合概率分布模型，进而分析水文事件在不同遭遇情况下的风险概率。刘曾美[10]采用Copula函数对感潮河段水位与上游洪水和河口潮位进行了关联性分析，为城市治涝感潮河段合理选取设计潮位提供了科学依据；林荣[11]等采用正态变换法对黄浦江潮位和区间暴雨遭遇概率进行了分析；任锦亮[12]等针对台风期间上海市防洪涝灾害问题，对降雨和潮位的遭遇组合进行了研究，分析了各致灾因子相互遭遇的风险概率。然而目前应用最大熵与Copula函数联合构建降雨和潮位相关联的风险性模型，进行降雨和潮位遭遇风险概率分析的研究还比较少。因此，本文基于广州市金坑测站与黄埔测站1970-2010年降雨量与潮位资料，应用最大熵与Copula方法对两变量进行关联性分析，对不同雨潮组合情况下的风险概率进行比较，以期为广州城区洪涝灾害的防治提供参考依据。

1 研究方法

1.1 最大熵原理

最大熵原理是由科学家ET Jaynes[13]于1957年首次提出，近年来作为兴起的参数估计方法被广泛应用于水文频率分析中的不确定性研究中。熵是用来描述一个物质系统不确定程度的物理量，熵越大，表示系统的不确定程度越大，因此，在给定约束条件的情况下，系统中各元素满足不确定度最大的分布就是最客观的分布，即最大熵分布[14]。国内外学者们通过大量的研究实验得出，在应用最大熵原理推导特征量的概率分布时，所得结果误差最小，精度较高，最能反映客观实际情况。因此，在水文频率分析中，采用最大熵法生成的概率分布更能够反映水文变量的统计特征。

基于最大熵原理，对于任意水文变量，有

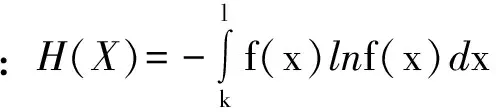
(1)

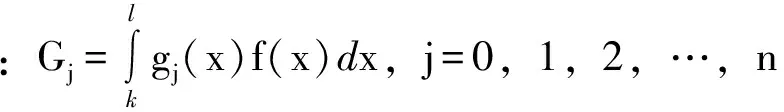
(2)

式中：f(x)为概率密度函数；gj(x)为x的第j个约束条件；n为约束条件的个数。

满足在约束条件Gj下目标函数H(x)取得最大值的参数取值则为基于最大熵原理的参数估计法，此时随机变量间的不确定性达到最大，即最接近随机变量自然特征的状态。

本文以最大熵原理对P-Ⅲ分布的密度函数进行估计，P-Ⅲ分布的概率密度函数为：

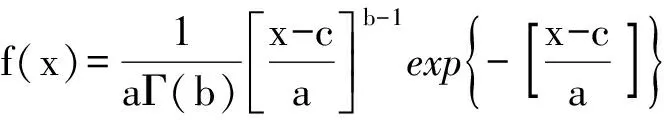
(3)

将式(3)取自然对数，乘以-f(x)后从c到∞积分，可得基于最大熵原理的约束条件如下：

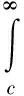
(4)

(5)

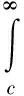
(6)

通过拉格朗日法可推导出最大熵对应的概率分布，可用式(7)表示，其中λ0、λ1、λ2为拉格朗日乘子。

f(x)=exp[-λ0-λ1x-λ2ln(x-c)]。

(7)

将式(7)代入约束条件(4)、(5)、(6)中则可求得乘子λ0、λ1、λ2的值，即可得到最大熵对应的P-Ⅲ分布概率密度函数。

1.2 Copula函数

1.2.1 Copula函数定义和类型

Copula函数早在1959年即被提出，但直到1990年代该方法才得以迅速发展，成为统计学中一个新的课题。Copula是定义域为[0,1]均匀分布的多维联合分布函数，它可以将多个随机变量的边缘分布连接起来得到它们的联合分布。

Sklar定理[15]：令H为一个n维分布函数，其边缘分布为F1，F2…,Fn。则存在一个n-Copula函数C，使得对任意x∈Rn，有

H(x1,x2,…,xn)=C(F1(x1),F2(x2),…,Fn(xn))。

(8)

式(8)中所定义的函数H是一个n维分布函数，其边缘分布为F1，F2，…,Fn。

Copula函数的优点在于不必要求各变量都具有相同的边缘分布，任意边缘分布经过Copula函数连接都可构造成联合分布，由于变量的所有信息都包含在边缘分布里，在转换过程中不会产生信息失真。在Copula函数中以Archimedean型函数应用最为广泛，其中的AMHCopula和FrankCopula函数适用于描述相关性较弱的变量，因此考虑降雨与潮位的实际特点，可采用AMHCopula与FrankCopula函数构建两变量联合概率分布。

Copula函数中参数θ的估计可采用相关性指标法[16]，即通过建立kendall秩相关系数τ与θ的关系，来求解参数θ的值。kendall秩相关系数τ[17]表示为：

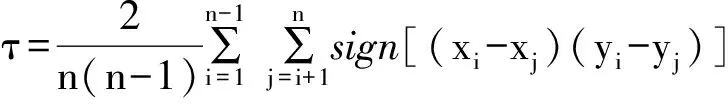
(9)

式中：τ为kendall秩相关系数，(xi,yi)为测点据，sign(·)为符号函数，n为系列长度。

估计各种Copula函数的参数θ后，我们可以建立基于Copula的不同变量间的联合分布函数[18]。表1是函数类型与参数θ的关系。

表1 函数类型与参数

表2 雨潮关联性分析模型

1.2.2 Copula函数拟合优度评价

为了确定最能准确反映变量间相关性的Copula函数，本文采用较为直观的图形分析法[19]进行拟合优度评价。该方法将理论概率值和经验概率值分别点绘于图中，若散点较均匀地分布在45°线附近，则表明两变量有较好的相关性。Femp(xi1,xi2)为两变量经验概率值，表示如下：

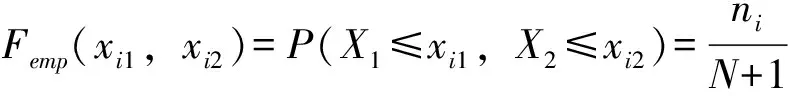
(10)

式中：N为实测序列的总对数；ni为序列中同时小于等于(xi1,xi2)的对数。

若要进一步确定最优Copula函数，可采用离差平方和最小准则法(OLS)[20]，OLS表达式如下：

OLS=

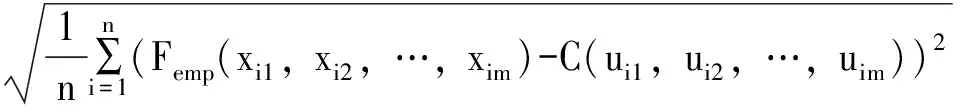
(11)

式中：Femp(xi1,xi2,…,xim)为经验频率值，C(ui1,ui2,…,uim)为理论频率值，m是维数，本文中m取2。OLS值越小，则表示Copula函数拟合越好。

1.3 雨潮关联性分析模型

对于排涝工程而言，设计暴雨和与之相对应的潮位以及设计潮位和与之相对应的降雨量之间的关系是确定工程规模的依据。当高潮位发生时，降雨量的大小并不固定；而暴雨发生时，河口处潮位高度也是多种多样。因此，研究各致灾因子间的遭遇组合概率是雨潮关联性分析的关键。

本文中降雨量用P表示，潮位用Z表示。定义年最大降雨量分布函数为FP1(p)，对应潮位为FZ1(z)；年最大潮位为FZ2(z)，对应降雨量为FP2(z)。在进行雨潮关联性分析时，针对降雨与潮位的不同组合情况，可以构建四种分析模型：

①治涝风险模型。降雨、潮位中至少有一个变量超过设定值时的概率，为年最大1h降雨量或相应潮位超过某一特定值的概率。

②同现风险模型。降雨、潮位中两变量同时超过设定值时的概率，反映洪涝威胁最大的情况，即降雨、潮位同时超过某一特定值的概率。

③遭遇风险模型。降雨、潮位中一个变量达到极值，在此条件下，另一个变量也达到极值的概率，反映两变量的上尾相关性，即研究区域的年最大1h降雨量(年最高潮位)高于某一特定值的情况下，站点相应潮位(相应1h降雨量)也不低于特定值的概率。

④组合风险模型。降雨、潮位中一个变量未超过设定值，另一个变量超出设定值的概率，反映年最大降雨量小于P1时对应潮位超过Z1的概率，或年最大潮位小于Z2时对应降雨量超过P2的概率。

对于排涝而言，不同组合情况下的雨潮关联性分析模型见表2。

2 实例分析

根据黄埔测站与金坑测站的(图1)年最高潮位资料和相应1h降雨资料以及金坑测站和黄埔测站的年最大1h降雨资料和相应潮位资料，采用P-Ⅲ分布建立年最高潮位FZ2(z)、相应1h降雨FP2(p)、年最大1h降雨FP1(p)、相应潮位FZ1(z)的边缘分布函数，采用最大熵法对其进行参数估计，参数估计结果见表3。

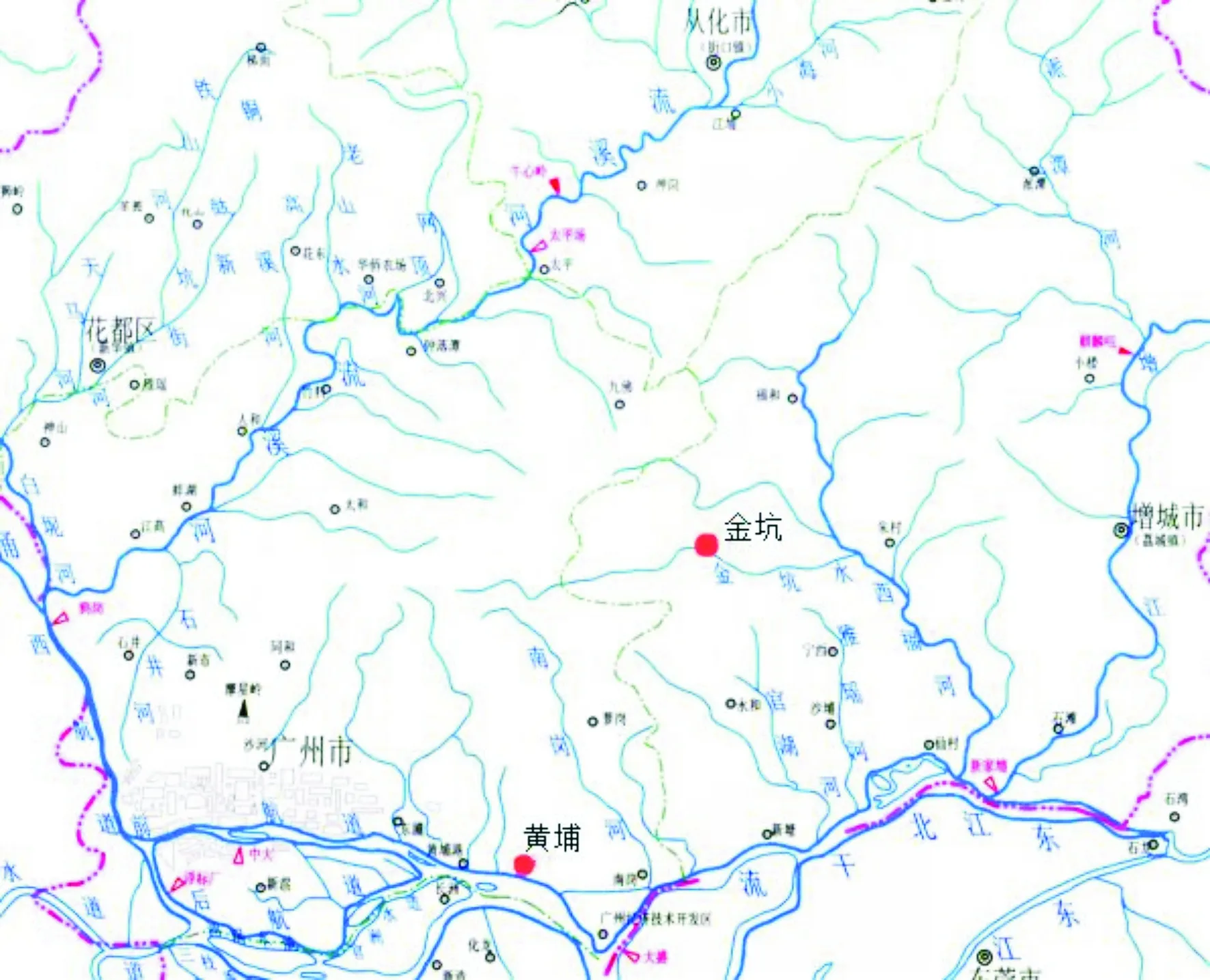
图1 水文测站位置示意图

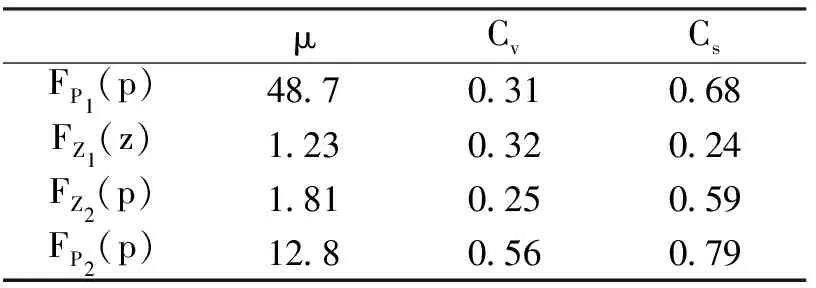
μCvCsFP1(p)487031068FZ1(z)123032024FZ2(p)181025059FP2(p)128056079

通过计算得到年最高潮位与相应1 h降雨量的秩相关系数τ为0.273，年最大1 h降雨量与相应潮位的τ为0.047。由此可见两组变量间均存在一定的正相关性，并且前者的正相关性相对较强，而后者的正相关性相对更弱。根据表1中τ和θ的关系，由AHM Copula拟合两组变量的参数θ分别为0.89和0.20，由Frank Copula拟合两组变量的参数θ分别为4.34和3.04，由此可分别建立基于Copula函数的理论联合分布。将利用表1中Copula公式计算得到的理论频率值和式(10)得到的经验频率值点绘于图2中可知，理论与经验概率散点均匀分布在45°线附近，表明两种Copula函数拟合的两序列相关性均较好。

采用OLS准则进一步确定拟合程度最佳的Copula函数，由式(4)得出AHM Copula与Frank Copula拟合年最高潮位和相应1 h降雨量的OLS值分别为0.036和0.048，拟合年最大1 h降雨量和相应潮位的OLS值分别为0.039和0.067，由于OLS值越小拟合程度越好，故采用AHM Copula函数构建降雨潮位的分析模型，图3为年最高潮位与相应1 h降雨量关联性分析模型，图4为年最大1 h降雨量与相应潮位关联性分析模型。

图2 雨潮组合的理论与频率分布图

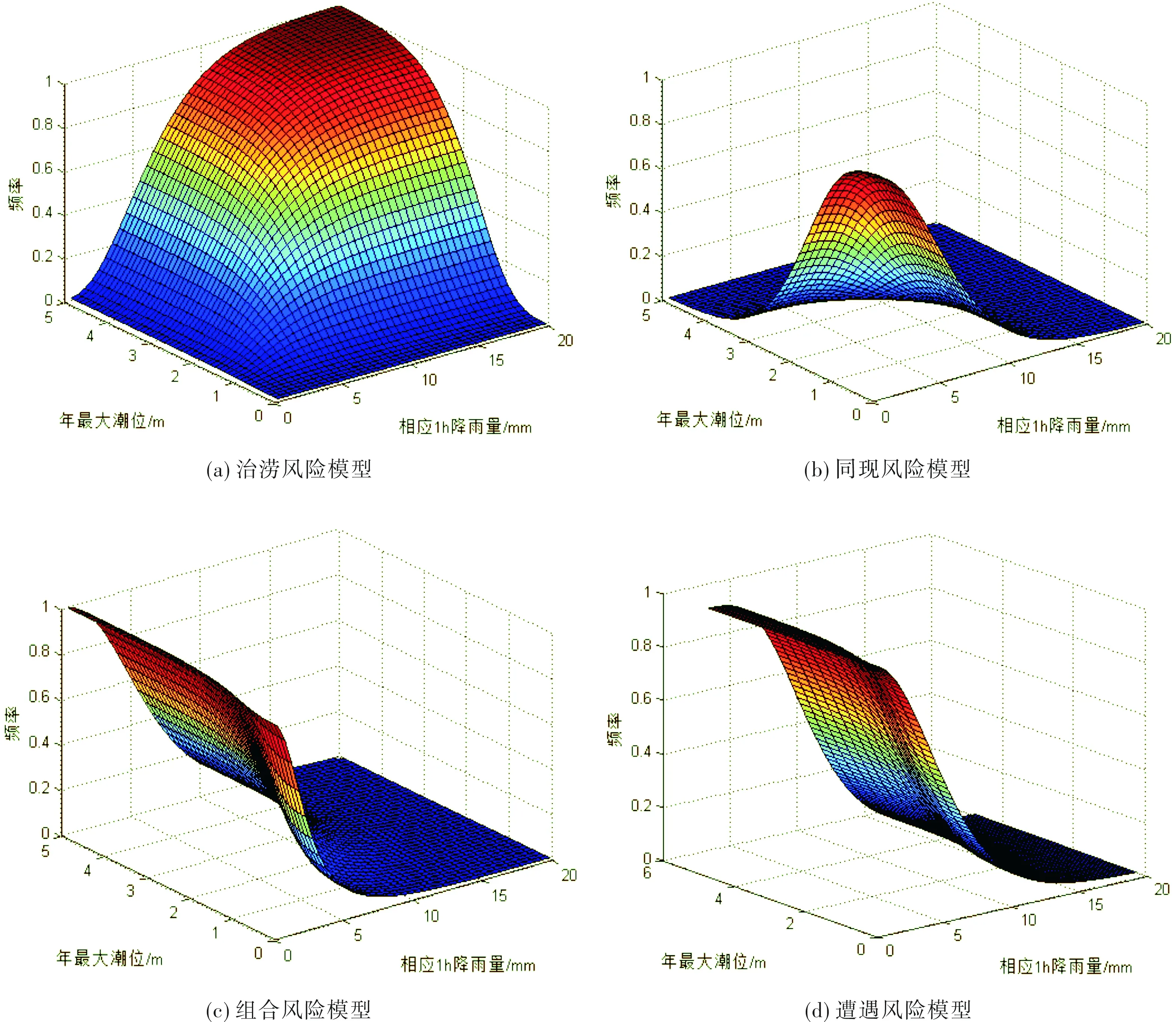
图3 年最高潮位与相应1 h降雨量关联性分析模型

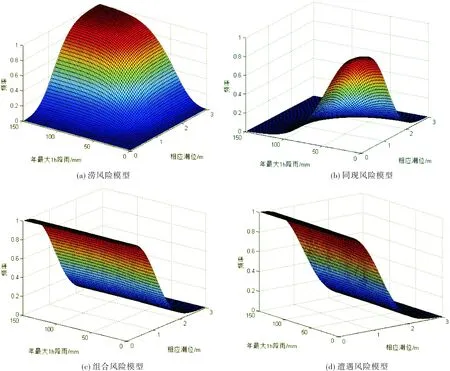
图4 年最大1 h降雨量与相应潮位关联性分析模型

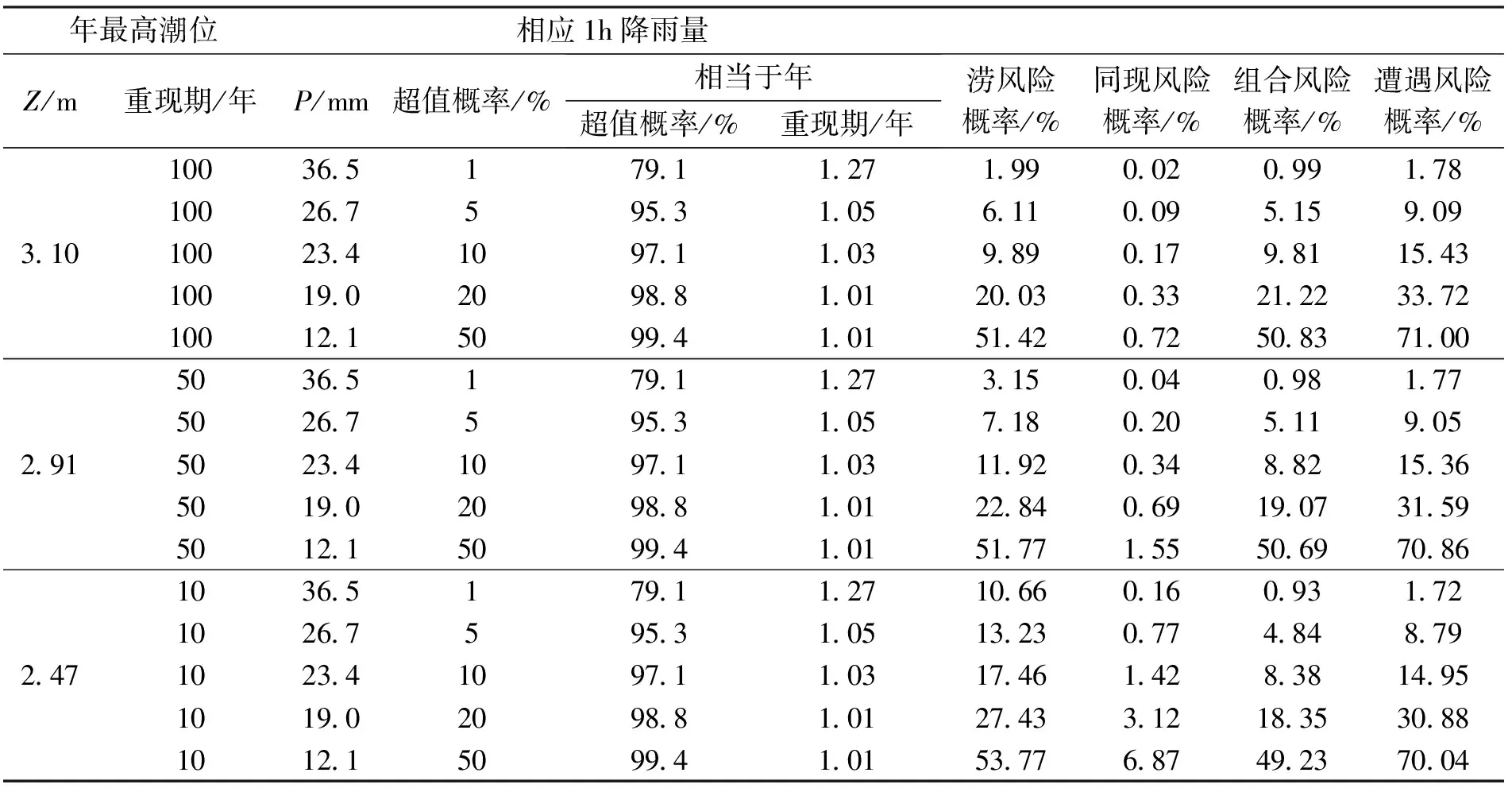
年最高潮位相应1h降雨量Z/m重现期/年P/mm超值概率/%相当于年超值概率/%重现期/年涝风险概率/%同现风险概率/%组合风险概率/%遭遇风险概率/%100365179112719900209917810026759531056110095159093101002341097110398901798115431001902098810120030332122337210012150994101514207250837100503651791127315004098177502675953105718020511905291502341097110311920348821536501902098810122840691907315950121509941015177155506970861036517911271066016093172102675953105132307748487924710234109711031746142838149510190209881012743312183530881012150994101537768749237004

由表2中的公式可以得出年最高潮位与相应1 h降雨量的治涝风险概率、同现风险概率、组合风险概率、遭遇风险概率(表4)。从表4中可以看出，治涝风险概率随年最高潮位与相应1 h降雨量重现期的减小而增大，如年最高潮位为10年一遇、相应1 h降雨为2年一遇时治涝风险概率最大，达到53.77%，发生的可能性较大；不同重现期组合下的年最高潮位与相应1 h降雨的同现分布概率均远小于单变量设计频率，可视为小概率事件，如超值概率均为1%时的年最高潮位与相应降雨量同现分布概率仅为0.02%，超值概率均为10%时的年最高潮位与相应降雨量同现分布概率为1.42%；对任一给定重现期的年最高潮位而言，组合风险和遭遇风险概率均随相应降雨量重现期的减小而增大，如给定年最高潮位为100年一遇， 重现期为100年、20年、10年、5年、2年一遇降雨的组合风险概率分别为0.99%、5.15%、9.81%、21.22%、50.83%；遭遇风险概率为1.78%、9.09%、15.43%、33.72%、71.00%。

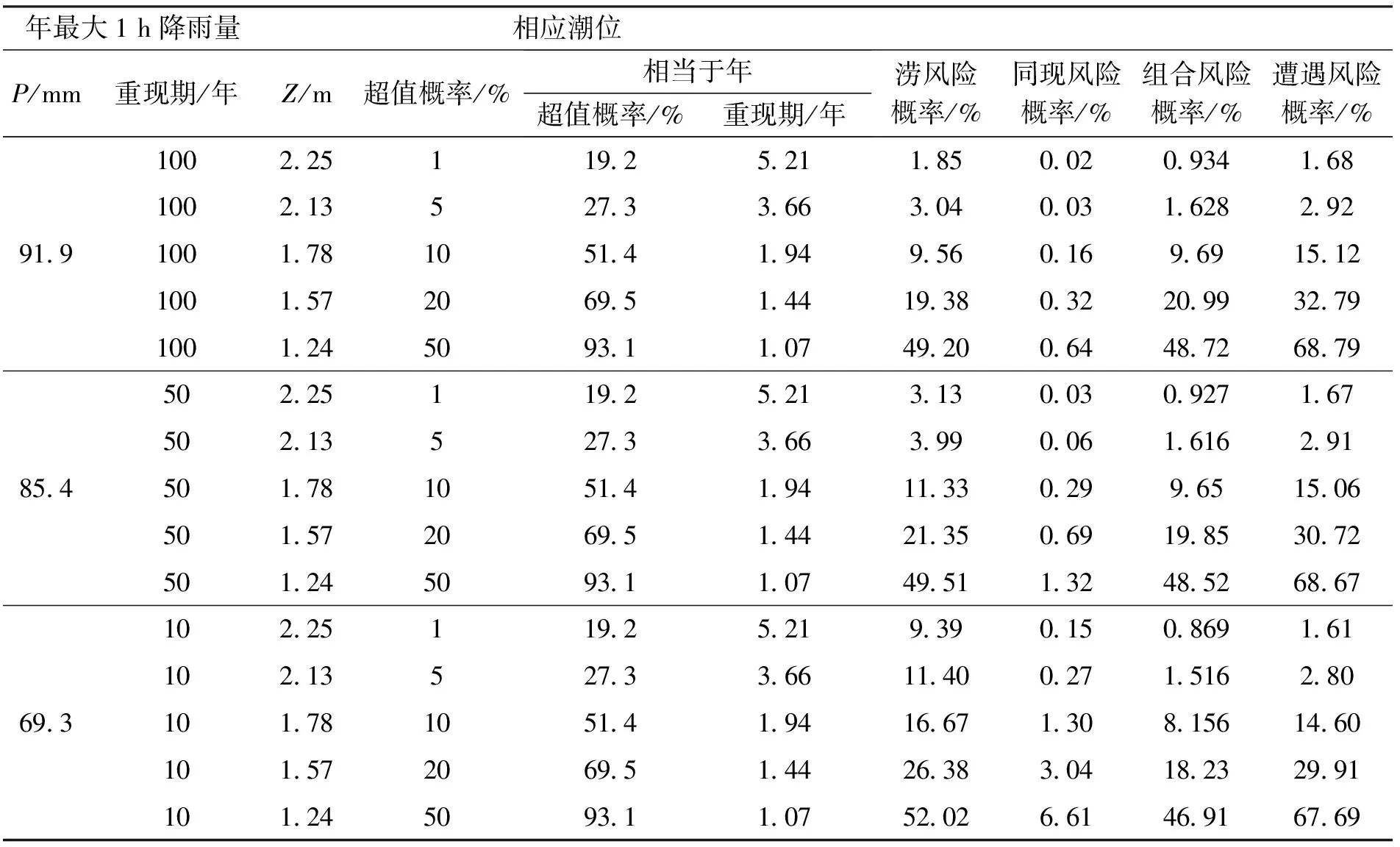
表5 年最大1 h降雨量与相应潮位风险概率计算成果

表5给出了各重现期下的年最大1 h降雨量与相应潮位的风险概率，由表5可以看出，年最大1 h降雨量和相应潮位的四种风险概率与表4具有相似的分布规律，在此不再赘述。对比两表中遭遇风险概率可见，在指定重现期条件下，最高潮位与相应1 h降雨的遭遇概率均大于最大1 h降雨与相应潮位的概率，如当年最高潮位为10年一遇时，金坑站1 h降雨达到100年、20年、10年、5年、2年一遇的遭遇概率分别为1.72%、8.79%、14.95%、30.88%、70.04%；当年最大1 h降雨为10年一遇时，黄埔站相应潮位达到100年、20年、10年、5年、2年一遇的遭遇概率分别为1.61%、2.80%、14.60%、29.91%、67.69%。由此可见，年最大1 h降雨量与相应潮位的相关关系较年最高潮位与相应1 h降雨量的相关关系更弱，这与前文求得的两种组合的kendall秩相关系数τ的大小相吻合。在实际工程设计中，若以潮为主，则在指定设计潮位条件下提高设计降雨标准可降低两变量对应的风险概率，如表4中取设计潮位为3.1 m，若将设计降雨从19.0 mm提高至23.4 mm，则治涝、组合、遭遇风险概率可分别从20.03%、21.22%、33.72%降至9.89%、9.81%、15.43%。若以降雨为主，则在指定设计降雨条件下提高设计潮位标准可降低两变量对应的风险概率，如表5中取年最大1 h降雨为91.9 mm，若将相应设计潮位从1.24 m提高到1.57 m，则治涝、组合、遭遇风险概率可分别从49.20%、48.72%、68.79%降至19.38%、20.99%、32.79%。

3 结论

强降雨和外江潮位高度直接影响着广州城区受洪涝灾害的程度。通过年最大潮位和相应1 h降雨量与年最大1 h降雨量和相应潮位的关联性分析，可为易涝区治涝设计提供参考依据。

本文利用AMH Copula-最大熵原理构建关联性分析模型，对不同重现期下的雨潮组合进行关联性研究，通过研究给出了两种组合下的四种风险概率，通过分析得出治涝风险概率随年最高潮位(年最大1 h降雨)与相应1 h降雨量(相应潮位)重现期的减小而增大；不同重现期组合下的年最高潮位(年最大1 h降雨)与相应1 h降雨(相应潮位)的同现分布可视为小概率事件；且对比计算成果表中遭遇风险概率可见，在指定重现期条件下，最高潮位与相应1 h降雨的遭遇概率大于最大1 h降雨与相应潮位的遭遇概率，表明年最高潮位与相应1 h降雨量的相关关系强于年最大1 h降雨与相应潮位的相关关系；此外，在实际工程设计中，若以潮为主，可提高设计降雨标准以降低两变量对应的风险概率；以降雨为主，可提高设计潮位标准以降低两变量对应的风险概率。

[1] 夏军,任国玉.气候变化对我国水资源影响研究面临的机遇与挑战[J].地球科学进展,2011,26(1):1-12.

[2] 程晓陶,王静,夏军,等.气候变化对淮河防洪与排涝管理项目的影响及适应对策研究[J].气候变化研究进展,2008,4(6):324-329.

[3] 王菜林,任学慧,李颖,等.基于PPD的辽宁省暴雨灾害风险分析[J].灾害学,2015,30(1):217-221.

[4] 陈刚.广州市城区暴雨洪涝成因分析及防治对策[J].广东水利水电,2010,7(7): 38-41.

[5] 张维,欧阳里程.广州城市内涝成因及防治对策[J].广东气象,2011,33(3):49-53.

[6] 肖可以,宋松柏.最大熵原理在水文频率参数估计中的应用[J].西北农林科技大学学报(自然科学版),2010,38(2),197-205.

[7] 张明,张阳.水文频率分析中参数估计最大熵法的梅林变换推导[J].水资源与水工程学报,2015,26(4):105-107.

[8] 陶山山,多维最大熵模型及其在海岸和海洋工程中的应用研究[D].青岛:中国海洋大学,2013:34-38.

[9] 童心.Copula函数与信息熵理论在洪水多元分析和径流随机模拟中的研究[D].南京:南京大学,2015:58-61.

[10]刘曾美,覃光华.感潮河段水位与上游洪水和河口潮位的关联性研究[J].水利学报,2013,44(11),1278-1284.

[11]林荣,李国芳.黄浦江风暴潮位,区间降雨量和上游来水量遭遇分析[J].水文,2000,20(3):1-5.

[12]任锦亮,李琼芳,李鹏程，等.上海市台风降雨和潮位遭遇组合概率研究[J].水电能源科学,2013,31(7):1-4.

[13]Jaynes E T.On the rationale of maximum entropy methods[J].Proceedings of the IEEE,1982,70(9):939-952.

[14]王栋,朱元甡.最大熵原理(POME)在水文水资源科学中的应用[J].水科学进展,2001, 12(3):424-430.

[15]Sklar M. Fonctions de répartition à n dimensions et leurs marges[M]. Université Paris 8,1959, 8:229-231.

[16]杜江,陈希镇,于波.Achimedean Copula函数的参数估计[J].科学技术与工程,2009,9(3):637-640.

[17]刘曾美,陈子燊.基于两个致灾因子的治涝标准研究[J].水力发电学报,2011,30(3):39-44

[18]郭恩亮,周沫,张继权,等.基于Copula函数的长春市暴雨联合分布与特征分析[J].灾害学,2015,30(4):173-177.

[19]张冬冬,鲁帆,严登华,等.基于Archimedean Copula函数的洪水多要素联合概率分布研究[J].中国农村水利水电,2015(1):68-74.

[20]陆桂华,张亚洲,肖恒,等.气候变化背景下蚌埠市暴雨与淮河上游洪水遭遇概率分析[J].气候变化研究进展,2015,11(1),31-36.

Correlation Study of Rainstorm and Tidal Level Using the Maximum Entropy-Copula Method——A Case Study of Guangzhou

HUANG Jinlin1, 2, FAN Jiawei3and TANG Zaozao1, 2

(1.GuangdongResearchInstituteofWaterResourcesandHydropower,Guaugzhou510635,China; 2.StateandLocalJointEngineeringLaboratoryofEstuaryHydropowerTechnology,Guangzhou510635,China; 3.SchoolofCivilEngineering,TianjinUniversity,Tianjin300072,China)

RainstormandtidesaretwofactorsofGuangzhou’surbanwaterlogging.ThecorrelationoftherainstormandtidesiscarriedoutinordertoprovidebasisforriskanalysisofwaterlogginginGuangzhou.Themodelaboutthecorrelationoftheannualmaximumtidallevelandthecorrespondingone-hourrainfall,annualmaximaofone-hourrainfallandtidallevelareestablished.MaximumEntropy-AMHCopulaisusedtobuildconditionalwaterlogpreventionriskmodel,simultaneousriskmodel,jointriskmodelandencounteredriskmodel.Theresultsshowthatthesimultaneousriskprobabilityoftwokindsofcombinationsislessthanthesinglevariablefrequency;Comparedtothecorrelationbetweentheannualmaximumtidallevelandthecorrespondingone-hourrainfall,aweakercorrelationisbetweentheannualmaximaofone-hourrainfallandtidallevel.Intheactualengineeringdesign,improvingthetidelevel(rainfall)standardcanreducetheriskprobabilityofthetwovariables.

maximumentropy;Copula;combinationofrainfallandtide;correlation;probability;Guangzhou

10.3969/j.issn.1000-811X.2017.01.012.]

2016-06-26

2016-09-30

广东省水利科技创新项目(2015-12)

黄锦林(1971-)，男，江西赣县人，教授级高级工程师，博士，从事水利工程与防洪减灾研究工作. E-mail：hjl@gdsky.com.cn

TV122；X43

A

1000-811X(2017)01-0065-07

10.3969/j.issn.1000-811X.2017.01.012

黄锦林，范嘉炜，唐造造. 基于最大熵-Copula方法的降雨潮位关联性分析——以广州为例[J]. 灾害学，2017，32(1)：65-71. [HUANG Jinlin，FAN Jiawei，TANG Zaozao. Correlation study of rainstorm and tidal level using the maximum entropy-copula method——A case study of Guangzhou [J]. Journal of Catastrophology，2017，32(1)：65-71.