井眼轨迹控制工具导向运动控制研究

冯 定，卢 昌，张 红，3，黄 锴

(1.长江大学 机械工程学院，湖北 荆州 434023；2.湖北省油气钻完井工具工程技术研究中心，湖北 荆州 434023；3.水电机械设备设计与维护湖北省重点实验室(三峡大学)，湖北 宜昌 443002)

井眼轨迹控制工具导向运动控制研究

冯 定1，2，卢 昌1，2，张 红1，2，3，黄 锴1，2

(1.长江大学 机械工程学院，湖北 荆州 434023；2.湖北省油气钻完井工具工程技术研究中心，湖北 荆州 434023；3.水电机械设备设计与维护湖北省重点实验室(三峡大学)，湖北 宜昌 443002)

基于井眼轨迹控制工具的结构特点，建立导向机构的数学模型，分析了导向过程中偏置机构合位移的形成及其分解方法。考虑了工具外套变形对主轴偏置运动的影响，以及不旋转外套发生微小转动的情况，推导出调整主轴到目标点的控制方程。根据内外偏心环初始位置及目标点坐标选择最优路径，从而使调整时间最短。利用井眼轨迹控制工具试验装置的试验数据得出仿真曲线，验证了推导方程的正确性。

井眼轨迹；控制工具；偏置机构；导向控制

旋转导向钻井技术是在20世纪80年代末期发展起来的一项新兴钻井技术，代表了当今世界钻井技术的最高发展阶段，是世界各国争相发展的全新自动化钻井新技术[1-3]。根据导向方式的不同可分为推靠式和指向式。国外多家公司已拥有各自成熟的产品，国内对指向式井眼轨迹控制工具的研究还不够完善，存在较多技术难题[4-9]。本文根据井眼轨迹控制工具导向原理，综合考虑不旋转外套变形对偏置芯轴运动的影响，分析了导向过程中主轴运动情况。

1 井眼轨迹控制工具导向机构及其原理

井眼轨迹控制工具通过偏置机构对井眼轨迹进行精确导向控制[10]。偏置机构主要由内外2个偏心环组成。内环嵌于外环里面，同时主轴嵌在内环里面。内外偏心环具有相同的偏心距，通过调整内外偏心环的位置可以实现增斜、稳斜和降斜的目的。外环与内环之间、内环与主轴之间装有滚动轴承。偏置机构结构如图1所示。

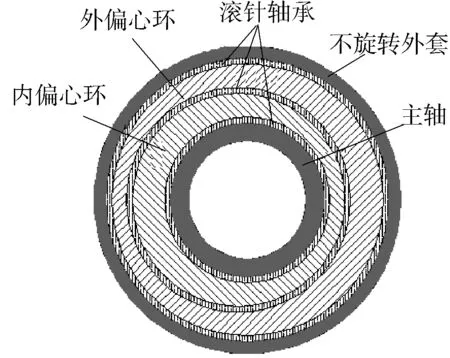
图1 偏置机构示意

井眼轨迹控制工具接收导向指令后，将钻杆动力通过主轴联轴器、电磁离合器及减速器传递给偏置机构，控制单元通过控制电磁离合器的吸合实现内外偏心环的相对转动，从而实现主轴任意角度的弯曲，使钻头达到所设定的偏转角和方位角。导向控制工作原理如图2所示。

图2 井眼轨迹控制工具原理

2 偏置机构导向芯轴偏心位移矢量控制

在井眼轨迹控制工具的偏置机构中，改变内外环各自的旋转角度，形成一个大小和方向都可控的偏心合位移矢量，从而控制钻井工具的工具面角和偏转角。在作业过程中，根据所需造斜率确定对应的偏心位移矢量，再将其分解为内外偏心环对应的旋转角度。由于工具外壳与主轴会产生相互作用，导致实际偏转角与理论偏转角有所偏差，摩擦力的存在会使得工具外壳产生一定的旋转角度，影响工具面角的设定。

2.1 偏置机构偏心矢量合成

以导向执行机构中心轴线与控制平面的交点为原点，建立主轴偏心位移示意图，如图3所示。

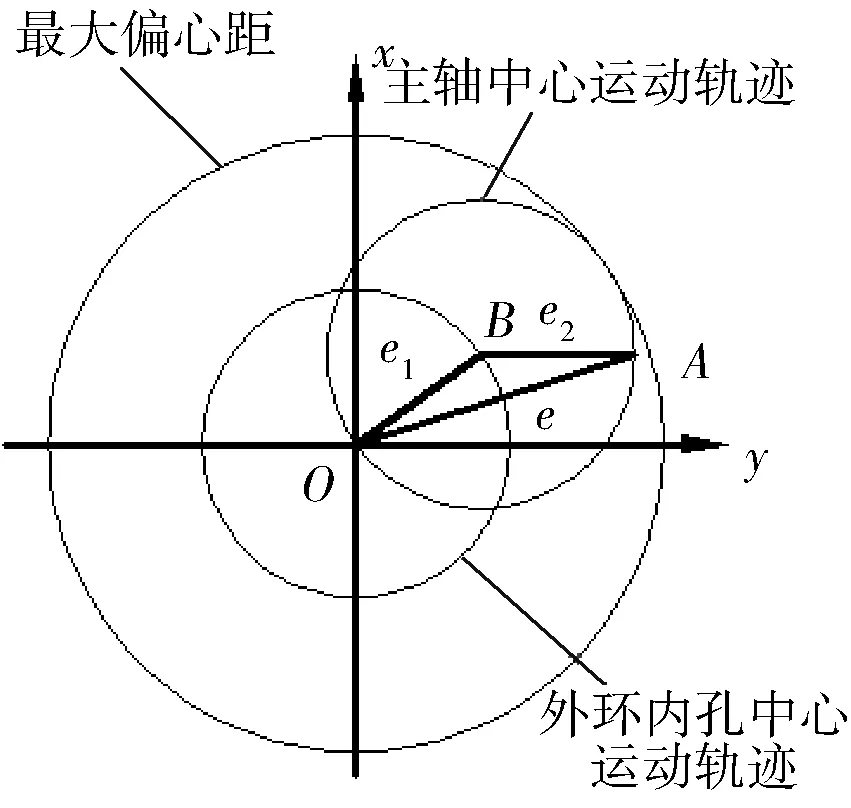
图3 主轴偏心位移示意

(1)

分解矢量到x轴和y轴得：

ex=ecosα=e1cosα1+e2cosα2

(2)

ey=esinα=e1sinα1+e2sinα2

(3)

即：

(4)

计算得出：

(5)

偏置机构的动力来源于主轴，由联轴器将钻杆的旋转运动通过电磁离合器传递给减速装置，再经过减速装置作用在内外偏心环上。为保证偏心环旋转角的控制精度，应控制其角速度ω在2π rad/min以内。

在初始状态下，当内环保持不动，单独旋转外偏心环，经过t1时间后旋转角度为α1=ωt1，代入式(2)～(3)得主轴偏心位移矢量，分解到x轴和y轴分别为：

ex=ecosα=e1cos(ωt1)-e2

(6)

ey=esinα=e1sin(ωt1)

(7)

计算得出：

(8)

当外环保持不动，单独旋转内偏心环，经过t2时间后旋转角度为180°+ωt2，代入式(2)～(3)得主轴偏心位移矢量，分解到x轴和y轴分别为：

ex=ecosα=e1-e2cos(ωt2)

(9)

ey=esinα=e2sin(ωt2)

(10)

计算得出：

(11)

在导向过程中，通过传感器实时检测内外偏心环的旋转角度，经过换算获得主轴的位移矢量并与预设定值比较，出现偏差则进行动态调整。

2.2 偏置机构偏心矢量分解

在钻井过程中，计算机会根据所设定的造斜率来得出偏心位移合矢量，然后转化为内外偏心环的旋转角度。确定内外偏心环的旋转角度后，工具就能按照对应造斜率钻进。但在偏心环偏置过程中，主轴产生弯曲变形的同时，工具外壳也会产生相对应的变形。因此在设定偏心位移合矢量时需要考虑工具外壳变形所抵消掉的部分位移。

图4为本工具简化后的模型示意图，偏心环在给主轴施加偏置力F的同时会对工具外壳产生一个反向的偏置力F。

图4 简化模型示意

图4中：L1为下轴承到偏心环的距离，mm；L2为上轴承到偏心环的距离，mm；L为两轴承之间的距离，L=L1+L2，mm；θ1、θ2为钻头轴线与工具轴线的夹角，(°)；θ3、θ4为工具外壳与工具轴线的夹角，(°)。

模型可看成简支梁变形问题，则主轴在偏心环处所产生的挠度ωB为：

(12)

根据叠加原理可以得：

e=ωA+ωB

(13)

通过给定的造斜率计算得出钻头偏转角。在已知的情况下，偏置力F的计算公式为[11]：

(14)

在偏置力F的作用下，工具外壳产生的挠度ωA为：

一时间,苞米、葵花盘长了翅膀似的飞向徐进步,徐进步顾上顾不了下,狼狈地蹿到了几个箩筐后面。无辜挨打的男知青们也跟着东躲西藏。

(15)

转角θ4与θ2之间存在如下关系式：

(16)

代入式(15)可得：

(17)

根据式(12) ～(13)和(17)可得实际偏心位移合矢量模值e′为：

(18)

上述各式中：F为偏置力，kN；E1为工具外壳弹性模量，Pa；I1为工具外壳横截面惯性矩，mm4；E2为主轴弹性模量，Pa；I2为主轴横截面惯性矩，mm4。

通过给定的造斜率计算得出θ，代入式(18)可得到需要设定的偏心位移合矢量模值e′。

(19)

3 内外环运动轨迹优选

图5 为内外环中心运动轨迹示意图，A为偏置机构中心位置，B′为外环内孔中心，C′为主轴中心实际位置，可由传感器测得其坐标。假设C点为主轴中心运动目标点，则外环中心运动到B或者D两点时，再转动内环，都可以使主轴中心到达C点。

图5 偏心环中心运动轨迹示意

偏心环按顺时针方向旋转，则内外环需要旋转角度分别为：

(20)

或者

(21)

式中：θAB′为内偏心环偏移方向与x轴正方向夹角；θBC′为外偏心环偏移方向与x轴正方向夹角；θ为偏心合位移矢量与x轴正方向夹角；ec为偏心合位移模值；θ0为工具外壳实际旋转角度，顺时针方向为正。

由于内外环旋转角速度相同，根据式(20)～(21)，排除θ5～θ8中最大值，则另外一组解为调整的最佳方案。

4 主轴偏置运动试验

井眼轨迹控制工具试验装置主轴外径D=70 mm，内径d=40 mm；偏置机构内外偏心环的偏心距e均为3 mm。设定主轴转速为最大值200 r/min，模拟偏置机构从初始状态调整到偏心合位移转角为60°，偏移量为6 mm。图6为此工况下主轴动位移曲线，在5 s时开始调整偏心环位置，在5～15 s先由内外偏心环共同旋转60°，故此刻偏心合位移仍为0。在15～45 s，内偏心环开始调整旋转角度，此时偏心合位移开始有变化，直至偏心合位移达到最大值。45 s以后工具稳定造斜。

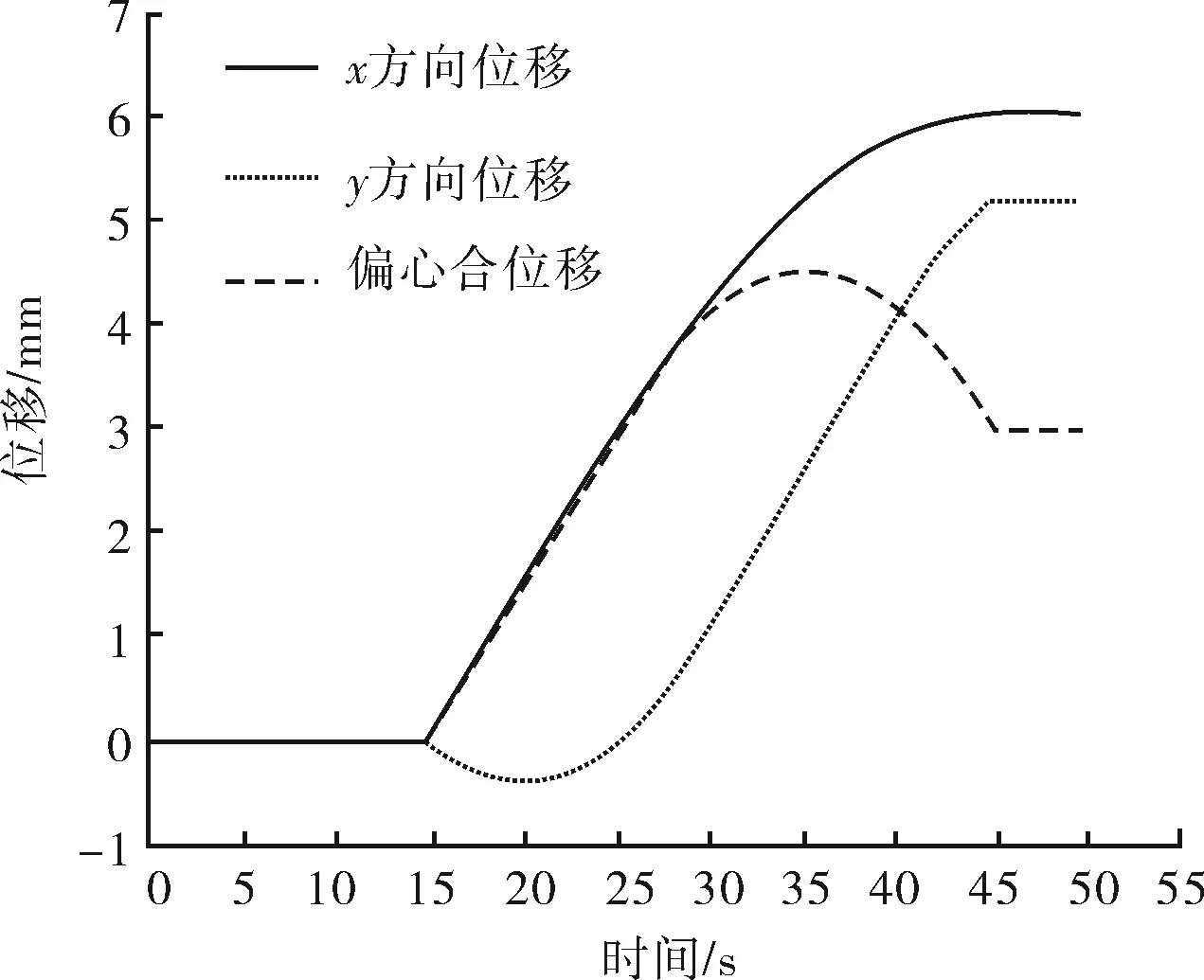
图6 α=60°主轴动位移曲线

模拟偏置机构从初始状态调整到偏心合位移转角为90°，偏移量为3 mm时的状态。图7为此工况下主轴动位移曲线，在5 s时开始调整偏心环位置，在5～10 s先由内外偏心环共同旋转60°，此刻偏心合位移仍为0。在10～60 s，内偏心环开始调整旋转角度，此时偏心合位移开始有变化，在40 s时工具达到最大偏心位置，随后偏心距开始减小。60 s时，合位移偏心距达到3 mm，偏移方向达到90°，故x方向位移变为0。此后工具达到稳定状态，开始造斜。

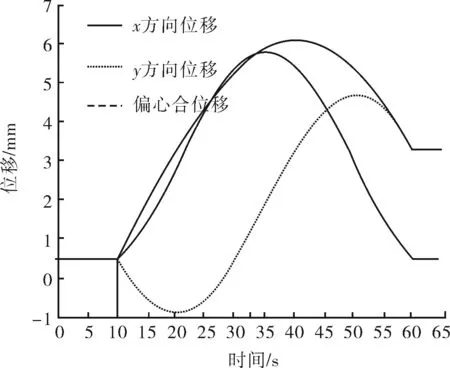
图7 α=90°主轴动位移曲线

当不旋转外套发生转动，或者需要调整造斜率时，控制系统需要根据当前外偏心环内孔中心点坐标、当前主轴中心点坐标和主轴中心目标点坐标来选择最优运动轨迹。现模拟系统从α=60°，偏移量为6 mm的工况一开始调整至α=90°，偏移量为3 mm的工况二的过程。

如图8所示，偏置机构从5 s开始调整，在5～20 s，外偏心环开始调整角度，此时内外偏心环整体运动，故偏心合位移始终保持为6 mm。在20～60 s为内偏心环角度调整过程，其中在50 s处主轴中心经过工具轴线中心，偏心合位移为0。60 s时达到预定状态，工具保持稳定状态造斜。

图8 主轴调整过程动位移曲线

5 结论

1) 井眼轨迹控制工具主要由2个偏心距相同的内外偏心环共同作用于主轴，达到造斜目的。推导了偏心合位移矢量与偏心环旋转角度之间的关系。

2) 考虑了导向过程中工具外壳的变形对偏心合位移的影响，得出实际偏移量与理论偏移量的转换方程。

3) 针对内外环运动轨迹提出了最优路径选择方法，缩短了工具导向调整时间。

4) 根据试验装置具体参数模拟了主轴偏置过程运动轨迹，验证了推导公式的正确性。

[1] 赵金海，唐代绪，朱全塔，等.国外典型的旋转导向钻井系统[J].国外油田工程，2002，18(11)：33-36.

[2] 王鹏，盛利民，窦修荣，等.国外旋转导向最新技术进展与发展趋势[J].钻采工艺，2013，36(6)：32-35.

[3] 李汉兴，姜伟，蒋世全，等.可控偏心器旋转导向钻井工具偏心位移控制分析[J].中国海上油气，2008，20(3)：183-187.

[4] 冯定，袁咏心，李汉兴，等.井眼轨迹控制工具发展现状及趋势[J].石油机械，2011，39(3)：70-73.

[5] Stuart Schaaf，Schlumberger，Mallary C R，et al.Pointthe-Bit Rotary Steerable System：Theory and Field Results[R].SPE 63247，2000.

[6] Christopher Jeffery，Michael Coss，Richard Rivera，et al.Pivot Stabilizer Innovations for Point the Bit Rotary Steerable Systems Result in Improved Drilling Performance for Specific Applications[R].SPE 163529.

[7] 张红，罗权，夏成宇，等.井眼轨迹控制工具内偏心环啮合与运动轨迹模拟[J].石油机械，2014，42(7)：12-15.

[8] 李士斌，王业强，张立刚，等.静态推靠式旋转导向控制方案分析及优化[J].石油钻采工艺，2015，37(4)：12-15.

[9] 赵金洲，孙铭新.旋转导向钻井系统的工作方式分析[J].石油机械，2004，32(6)：73-75.

[10] 冯定，罗权，张红，等.井眼轨迹控制工具滚针轴承的偏载失效分析[J].石油机械，2015，43(4)：10-13.

[11] 冯定，肖苏宸，夏成宇，等.高造斜井眼控制工具主轴力学分析与试验研究[J].石油机械，2014，42(10)：34-36.

Research on Control of Steering Movement of Well Trajectory Control Tool

FENG Ding1，2，LU Chang1，2，ZHANG Hong1，2，3，HUANG Kai1，2

(1.SchoolofMechanicalEngineering，YangtzeUniversity，Jingzhou434023，China；2 .OilandGasDrillingandWellCompletionToolsResearchCenter，Jingzhou434023，China；3.HubeiKeyLaboratoryofHydroelectricMachineryDesign&Maintenance，ChinaThreeGorgesUniversity，Yichang443002，China)

The mathematical model of steering mechanism was established and the formation and decomposition method of bias units in the steering process base on the structure characteristics of well trajectory control tool were analyzed.A control equation of the spindle to the target point is derived with considering the influence of the deformation of the shell on the spindle and the small rotation of nor-rotation shell.According to the initial position of the inner and outer eccentric straps and the coordinate of the target point the optimal path is selected to make the shortest adjusting time.To demonstrate the correctness of the equation，the simulation curves are presented by using the experimental data of the well trajectory control tool experiment device.

well trajectory；control tool；bias units；steering movement control

1001-3482(2017)01-0006-05

2016-08-05

国家自然科学基金项目“高造斜率井眼轨迹控制工具主轴井下力学行为研究”(51275057)；湖北省教育厅科学研究计划中青年人才项目(Q20151301)；水电机械设备设计与维护湖北省重点试验室开放基金项目(2016KJX12)联合资助

冯 定(1963-)，男，教授，博士生导师，主要从事石油机械及井下工具的设计、诊断及动态仿真的技术研究，E-mail：fengd0861@163.com。

TE921.201

A

10.3969/j.issn.1001-3482.2017.01.002