中学体育课程教学的AHP-Fuzzy评价模型研究
2017-02-13郝建大连市中山区第42中学辽宁大连116000
□郝建(大连市中山区第42中学辽宁大连116000)
中学体育课程教学的AHP-Fuzzy评价模型研究
□郝建(大连市中山区第42中学辽宁大连116000)
本研究将层次分析法和模糊数学模型相结合,开发出了AHP-Fuzzy模型,并应用于中学体育课程教学评价当中去。AHP-Fuzzy模型能够将一些边界不清、不易定量的因素定量化,从多个因素对被评价事物隶属等级状况进行综合性评价。通过实验表明,AHP-Fuzzy模型在实际应用中具有较高的应用价值。
中学体育教学评价AHP-Fuzzy模型
体育教学活动是一个复杂的各类现象的合集,它由多种不同的内在因素构成,各因素之间既相互影响又相互制约,最终将体育教学活动呈现在我们面前。综合评价就是对诸多因素所影响的事物或现象做出总的评判,即对评判对象的全体,根据所给的条件,给每一个对象赋予一个或几个非负实数(评价指标),再据此排队择优。目前,在我国高校以及中学等基层学校中,对于体育课的评价方式仍然以教师主观定性评价为主,这种评价方法对评课教师的主观经验依赖较大,同一节课不同的评课教师依据自己的主观经验容易产生分歧,而且这种定性评价方式过于宏观、过于笼统,不利于上课教师把握课堂的改进方向。体育教学综合评价是将体育教学活动中的各构成因素进行分解、分析构成因素在体育教学活动中的重要性、找出对体育教学活动影响较大的因素进而为改进体育教学活动中的方式方法提供依据的一种定量评价方法。本研究将层次分析法(AHP)和模糊数学模型(Fuzzy)相结合,运用AHP法对评价指标进行筛选和权重赋值,运用Fuzzy法对收集到的评价数据进行计算,最终得出教师体育课得分。希望AHP-Fuzzy模型的构建能够为今后的中学体育教学综合评价工作找到一套客观准确的评价方法。
1、研究对象与方法
1.1、研究对象
本研究以参与中学体育教学的所有教师为研究对象的总体,以大连市中山区和西岗区80位中学体育教师为研究样本。研究样本中,高级职称教师16人,占总人数的20%;中级职称教师62人,占样本总人数的77.5%。参与调查的教师中,研究生学历教师18人,占总人数的22.5%;本科学历的教师55人,占样本总人数的69%。
1.2、研究方法
(1)专家访谈法。
在本研究中期报告《中学体育课程教学评价指标体系的构建研究》的基础上,对10位专家采用座谈和访谈相结合的方式对中学体育课程教学评价指标体系进行了权重的赋值。
(2)数理统计。
研究运用SPSS21.0版本对所收集的专家访谈数据进行了描述性统计分析,并运用模糊数学模型对《中学体育课程教学综合评价表》所收集的数据进行了分析和评分。同时,研究运用Excel VBA自主开发了关于本研究的判断评价AHP模型,并利用此模型对研究指标的权重进行了赋值计算。
2、研究结果与分析
2.1、评价指标体系的构建
本研究的指标评价体系是建立在中期研究《中学体育课程教学评价指标体系的构建研究》之上的,但是在《中学体育课程教学评价指标体系的构建研究》中只是对评价指标的维度和指标集进行了确立,没有对指标体系中各项评价维度下的指标权重进行赋值。
本研究采用成对比较法对指标权重进行计算。
A表示矩阵中的指标要素,aij表示指标Ai对于指标Aj的重要性。假设在成对比较矩阵中指标间的重要性为C,则有公式:aij=Ci/Cj
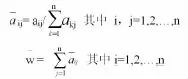
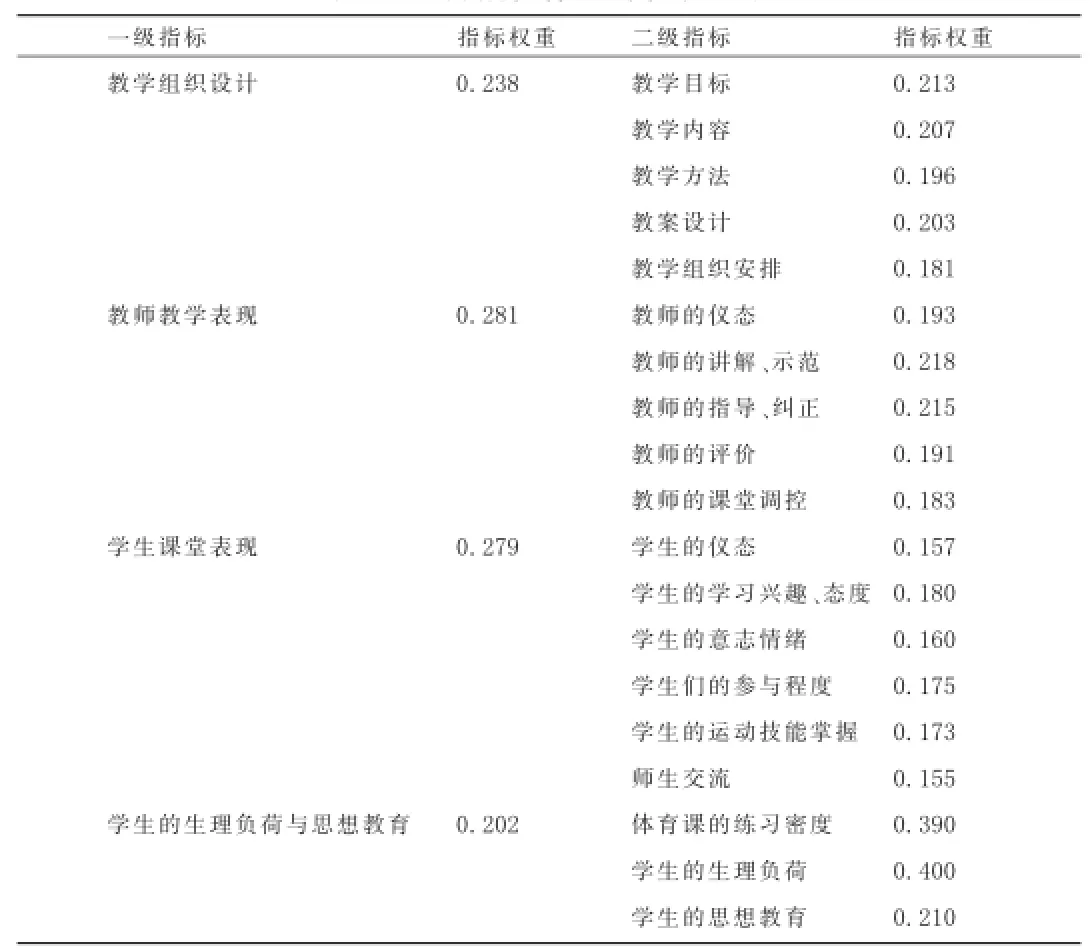
表1 评价指标体系的标权重表
在对指标进行权重赋值之后,我们应对判断矩阵进行一致性检验。一直性检验的指标为C.R.(Consistence Ratio),C.R.的计算公式如下:C.R.=C.I./R.I.指标集C.R.=0.069<0.1,因此评价体系的一级指标具有基本一致性。在二级指标中教学组织设计的C.R.值为0.076、教师教学表现的C.R.值为0.034、学生课堂表现的C.R.值为0.057、学生的生理负荷与思想教育的C.R.值为0.051,四组二级指标均小于0.1,达到了一致性水平。
2.2、评价数学模型研究
(1)数据收集和各指标集的建立。
以2015年4月大连市四十二中体育教师孙立国老师执教的体育课为例来印证本数学模型在实际应用中的有效性。在这节师范课上现场发放了调查问卷80份,问卷回收后,将每位教师所填写的信息进行了汇总。
在将问卷数据统计结束之后开始运用Fuzzy模型对指标数据进行计算。首先建立总指标集U={U1,U2,U3,U4},指标集U对应的权重集A=(0.238,0.281,0.279,0.202),指标集所对应的评语集为V={V1,V2,V3,V4,V5}分别表示五个评价级别:非常好、好、一般、差、非常差。
指标集U下四个指标集分别为:U1={u11,u12,u13,u14,u15};U2={u21,u22,u23,u24,u25};
U3={u31,u32,u33,u34,u35,u36};
U4={u41,u42,u43,}。
建立模糊集R,R所表示的是指标集U与评价集V一对一的对应关系,即函数R(V、U)。
(2)进行综合评价运算
根据矩阵复合运算法则可知,模糊集合R代表着集合U和集合V的模糊关系。因此,我们可以得知向量B就是集合R将集合U的模糊子集A映射到集合V上的一个模糊子集,向量B就是评判集V对因素集U的说明集。向量B的计算式为
所得到的n个数值归纳到一个集合中,该集合为:{b1,b2,b3,…,bn}
最后,通过归一化处理得出最后的评价结果:
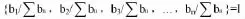
由于评价结果过于笼统会不利于教师间的横向比较,为了更加精确地计算本节体育课的水平,我们将对本节课所得到的综合评价结果最终得分进行计算。首先我们将评语集V中五个因素v1、v2、v3、v4、v5根据其对应的分数段进行赋分:v1非常好100-90分,v2好89-80分,v3一般79-70分,v4差69-60分,v5非常差59分以下。
最终评分结果为:
D=B·C
在本研究的课例中,由于调查指标集较多,调查样本大,为节省文章篇幅,将U1,U2,U3,U4所对应的B1、B2、B3、B4的计算过程不再一一列举直接将归一化处理后的终评判结果D1、D2、D3、D4呈现出来,四个指标集U1,U2,U3,U4评分结果分别为:D1=84.25分、D2=83.72分、D3=86.28分、D4=89.58分。
本节课的综合得分:
D=0.238×84.25+0.281×83.72+0.279×86.28+0.202×89.58
=85.744分
3、结论
(1)体育教学过程中受到很多内在和外在因素的影响,AHP-Fuzzy模型能够将定量和定性分析相结合,因此AHP-Fuzzy模型评价法在体育教学的评价中具有非常高的可操作性。
(2)通过本研究的实验表明,AHP-Fuzzy评价模型通过精确的数字手段处理模糊的评价对象,能对蕴藏信息呈现模糊性的资料做出比较科学、合理、贴近实际的量化评价。在体育教学综合评价中运用模糊数学模型进行评价,有利于将以往体育教学中的主观定性评价转变为客观的定量评价,使评价结果更加直观具体。
[1]王秉彝.体育科研数学方法[M].广州:广东高等教育出版社, 1998.
[2]Liu Z.A Comprehensive Evaluation Method for Physical EducationTeaching Based on Analytic Hierarchy Process[J]. International Journal of Digital Content Technology and its Applications,2013,7(2).
[3]张兆才.定性转定量评价一堂体育课质量的方法[J].首都体育学院学报,1988(3).
[4]孙庆祝.体育实用模糊数学[M].北京:人民体育出版社,1990.
[5]程致屏.体育应用高等数学[M].西安:陕西科学技术出版社, 1995.
[6]Zhang N,Zhang Z G.Application of AHP-Fuzzy Comprehensive Evaluation Method In Students Assessment[C]//Advanced Materials Research,2014,962.
G807
:A
:1006-8902-(2017)-01-SY
