基于虚拟水及营养学的水资源优化配置

张斌武，康鸿博，关秀翠

(1.河海大学常州校区数理教学部，江苏 常州 213022；2.河海大学物联网工程学院，江苏 常州 213022；3.东南大学数学系，江苏 南京 210096)

基于虚拟水及营养学的水资源优化配置

张斌武1，2，康鸿博2，关秀翠3

(1.河海大学常州校区数理教学部，江苏 常州 213022；2.河海大学物联网工程学院，江苏 常州 213022；3.东南大学数学系，江苏 南京 210096)

为综合考虑经济效益、虚拟水消耗量、人均用水公平性差异以及营养学因素在地区农畜产品生产规划中的作用，研究了基于虚拟水及营养学的水资源优化配置问题。建立了经济效益最大化、虚拟水消耗量最少、人均用水公平性差异最小并满足营养学约束的多目标优化模型。用可变模糊决策理论求解模型，得到最佳的各类农畜产品生产方案。以石羊河地区各数据为例对模型进行仿真，结果表明所得到的方案是综合性能最优的方案。

虚拟水；多目标优化模型；营养均衡；水资源优化配置；模糊决策；石羊河流域模拟仿真

水资源短缺是许多国家或地区面临的长期问题，如何可持续利用水资源是我国可持续发展战略中必须解决的一个重要问题。虚拟水概念首先是由Allan教授在1993年提出的[1]。虚拟水是指生产商品和服务所需要的水资源数量，并且是以虚拟形式存在于产品和服务中的非实体状态的水资源形式，它是隐藏在贸易背后看不到的水资源交易。近10多年来，国内学者从多个方面对虚拟水进行了研究并取得较显著的成果。徐中民等[2]从宏观上对虚拟水战略的影响及优缺点进行了全面分析；程国栋[3]考虑并分析了水资源社会化管理以及水资源的恢复重建。杨志峰等[4]在解析虚拟水、水足迹等概念内涵的基础上，系统地梳理了产品虚拟水核算、区域虚拟水贸易评估、虚拟水变化机制3个领域的研究进展。以上文献是从定性角度对虚拟水进行研究和分析。不少学者对虚拟水进行了定量研究。严冬等[5]借鉴基尼系数概念评价了虚拟水流动的区域均衡性。许多学者应用投入产出法对水资源消费、虚拟水贸易状况等进行了定量研究[6-8]。还有学者对工业产品虚拟水、农畜产品相关的虚拟水等方面给出了相应的计算方法[9-11]。杨明智等[12]考虑了社会，经济，生态3方面，对工业水资源配置进行了优化。但这些文献没有将经济效益、虚拟水消耗、人均用水公平性差异及营养学因素[13]综合考虑进行研究，因此笔者综合研究了涉及经济效益，虚拟水消耗量、人均用水公平性差异及营养学因素的水资源优化配置问题。

1 水资源优化配置问题模型的建立

笔者研究如下水资源优化配置问题：一个地区分为若干区域，如何制定各区域的生产规划(包括如何种植粮食及经济作物，如何安排畜牧养殖以及给各区域如何分配水资源)，在合理利用各区域耕种面积及分配的水资源等前提下，使该地区的经济效益最大、虚拟水消耗量最少、人均用水公平性差异最小以及所生产的农畜产品满足该地区的健康饮食类人群及素食主义类人群的营养需求。

在此建立水资源优化配置问题的一个多目标优化模型，该模型包括3个目标，分别是经济效益最大化、虚拟水消耗最小及人均用水公平性差异最小。在约束中考虑了饮食健康因素。下面给出模型的目标及约束条件。

目标一：经济效益最大化

总的经济效益为种植作物的净收入以及生产肉类的净收入之和。经济效益最大化目标可表示如下：

(1)

式中：xic、xie——i区域内c类粮食作物及e类经济作物的种植面积，hm2；yic、yie——i区域从其他地区净进口的c类粮食及e类经济作物总量(负值表示出口)，kg；xir、yir——i区域生产的r类肉类总量及从其他地区净进口r类肉类总量，kg；Uic、Uie——i区域内c类粮食作物及e类经济作物的产量，kg/hm2；Pic、Pie、Pir——i区域内c类粮食作物、e类经济作物及r类肉类的单位交易价格，元/kg；Cic、Cie——i区域内c类粮食作物、e类经济作物的种植成本，元/hm2；Cir——i区域内r类肉类的单位成本，元/kg；m——研究地区的区域数目；n1、n2、n3——研究地区内所种植的粮食、经济作物的种类及所生产的肉类的种类。

目标二：虚拟水最小化

虚拟水消耗总量为种植作物以及生产肉类所含虚拟水总量之和。虚拟水最小化可用如下公式表示：

(2)式中：VWC，ic、VWC，ie、VWC，ir——i区域内c类粮食作物、e类经济作物以及r类肉类的虚拟水含量，m3/kg。

目标三：人均用水公平性差异最小化

人均用水公平性差异最小化目标可用如下公式表示：

(3)

式中：wi——i区域内虚拟水的分配量，m3；W——所研究地区可用水总量，m3；Pi——i区域内的人口总量，人；P——所研究地区的人口总量，人。

下面分别给出模型中的各约束条件。

所研究地区内任意区域的任意一种粮食作物的总量必须满足该区域内全部人口为饮食健康而对该类作物最低消耗量以及某些区域对该类作物硬性的囤积量。

xicUic+yic-Kic-ND，icPD，i-NV，icPV，i≥0 ∀i，∀c

(4)

式中：Kic、Kie、Kir——i区域内规定硬性囤积的c类粮食作物、e类经济作物及r类肉类总量，kg；ND，ic、ND，ir——i区域内健康饮食(DCE)方案下人们对c类粮食作物及r类肉类的最少需求量，kg/(人·a)；NV，ic，NV，ir——i区域内素食主义(VEG)方案下人们对c类粮食作物及r类肉类的最少需求量，kg/(人·a)；PV，i、PD，i——i区域内素食主义人口及健康饮食人口总量，人。

所研究地区内任意区域的任意一种肉类的总量必须满足该区域内全部人口为饮食健康而对该类肉类最低消耗量以及某些区域对该肉类硬性的囤积量。

xir+yir-Kir-ND，irPD，i-NV，irPV，i≥0 ∀r，∀i

(5)

任意区域的任意一种经济作物的总量必须要满足该类经济作物的硬性囤积量。

xieUie+yie-Kie≥0 ∀e，∀i

(6)

任意区域的实际种植面积总量不超过可种植面积。

(7)

式中：Ai——i区域内可种植的总面积，hm2。

研究地区内所有区域消耗水量之和不超过研究地区内总共灌溉用水量。

(8)

研究地区内各区域的用水总量不超过整个研究地区的可用水总量。

(9)

本文建立的水资源优化配置模型为：以式(1)～(3)为3个目标，以式(4)～(9)为约束条件。

2 模 型 求 解

为求解模型，先将该多目标模型转化成求解若干个单目标优化模型，从而得到若干个可行方案。然后利用可变模糊决策理论[14]方法综合考虑3个目标，从多个方案中选择出综合性能最优的1种方案。

本文考虑的指标依次是经济效益最大化，虚拟水消耗最小，人均用水公平性最小，根据这3个指标提出了如下两大类方案：(a) 解以3个指标中的1个作为目标，从剩余2个指标中选取1个作为约束得到的单目标优化模型，得到的若干可行方案。(b) 解以3个指标中的1个作为目标，另外2个指标均作为约束得到的单目标优化模型，得到的若干可行方案。

以上两大类方案的具体方案的得到过程详见第3节。

求解模型时首先通过编写程序仿真得到不同方案的3个目标对应的特征值xkj，xkj表示第j个方案中第k个目标的数值。设模型的目标数为M(本文M=3)，拟定的方案数为N，则其特征量矩阵可表示为X=(xkj)M×N。

本文用到如下的2个用于计算多目标决策的相对隶属度公式(分别是特征量越小越优及特征量越大越优)，当目标为越大越优的时候选择式(10)，当目标为越小越优时选择式(11)：

(10)

(11)

式中：rkj——第j个方案中第k个目标的相对隶属度；xkmax——所有方案中第k个目标的最大特征量；xkmin——所有方案中第k个目标的最小特征量。

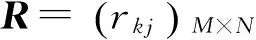
接着利用以下可变模糊决策模型公式[15]计算各方案的相对优属度：

(12)

(13)

(14)

式中：vA(u)j——方案的相对优属度；ωk——归一化经验权系数；α——优化准则参数；p——距离参数；dgj——决策j的距优距离；dbj——决策j的距劣距离。

式中α和p一般取1或2，每种组合下各方案都有不同的相对优属度，最优方案为优属度的平均值最大的方案。ωk决定了每个指标在方案中的重要性，根据实际情况ωk的取值可以多样化，而ωk的不同取值可能会得到不同的综合性能最优方案。

3 仿真与结论分析

以石羊河流域为例进行模拟仿真。为与所研究问题说法一致，本节称石羊河流域为地区，称该流域的凉州、民勤、古浪、天祝、金川、永昌6个市为6个区域。本文用到的具体数据主要来源于凉州、民勤、古浪、天祝、金川、永昌这六个区域的政府水务网站及Su等[15]。石羊河地区有6个区域，种植4类粮食作物及2类经济作物，生产6类肉类产品，即模型中m=6，n1=4，n2=2，n3=6。本文对给出的水资源优化配置模型利用MATLAB编程仿真，得到了18个可行方案，其中在第一大类方案中选取了6种方案，在第二大类方案中选取了12种方案。分别得到凉州、民勤、古浪、天祝、金川、永昌这6个区域在各个方案下，变量xic、yic、xie、yie、xir、yir、wi的具体数值，并得到各方案中6个区域的经济效益值、虚拟水消耗量及公平性差异值。

这里给出方案2的选取及结果。先建立以经济效益最大化为单目标、以f3≤0.9及式(4)～(9)为约束条件的单目标优化模型，然后求解该模型，得到方案2。该方案的经济效益为2.735×1011元，虚拟水消耗量为1.547×1010m3，人均用水公平性差异为0.9。

根据可变模糊决策理论将18个方案的经济效益值、虚拟水消耗量及公平性差异值(特征量)利用式(10)、式(11)转化为对应的相对隶属度数值(见表1)。

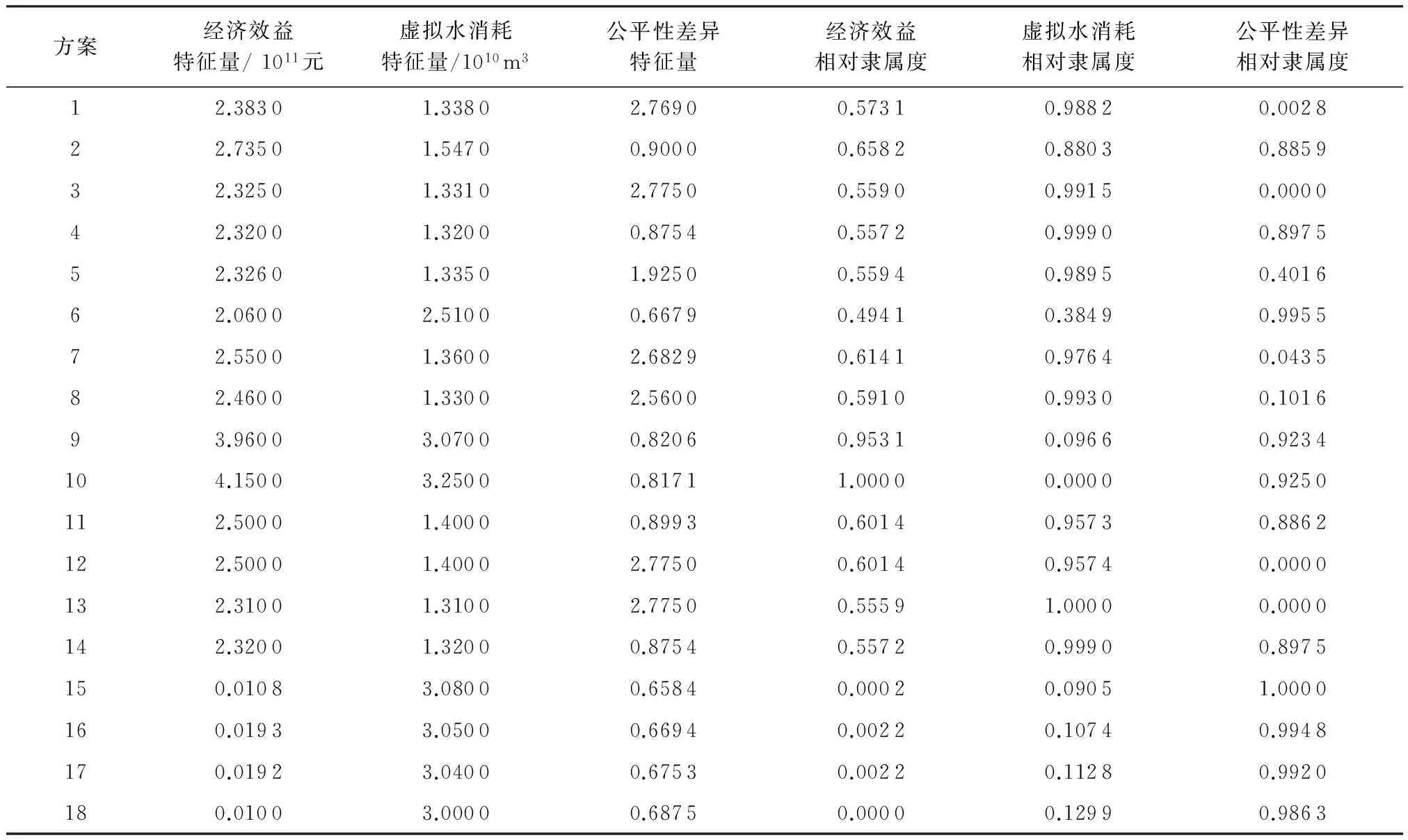
表1 18个方案中每个目标对应的特征量及相对隶属度

再根据式(12)～(14)将18个方案中各目标对应的相对隶属度转化成对应的相对优属度。在转化的过程中用到ωk、优化准则参数α及距离参数p。α取1或2、p取1或2得到4种组合，根据4种组合下各方案的相对优属度的平均值的最大值得到综合性能最优的方案。

当以经济效益最大这一指标为首要目标，认为其最重要，它与虚拟水消耗最小指标相比显著重要，与人均用水公平性相比较为重要[15]，从而确定经验权系数ω0=(1，0.538，0.333)。通过归一化进一步得到ωk=(0.535，0.288，0.177)，从而得到各方案的相对优属度，见表2。

通过表2可以得出，当ωk=(0.535，0.288，0.177)时方案2最优。注意到方案2是解以经济效益最大指标为目标、以人均用水公平性差异最小指标为约束的单目标优化模型所得到的方案。该方案认为经济效益最大指标最重要，而虚拟水消耗最少及人均用水公平性差异最小这2个指标与之相比不太重要，故模型给出的方案与该方案最初的选定方式相一致。仿真结果也表明模型所得到的方案是综合性能最优的方案。

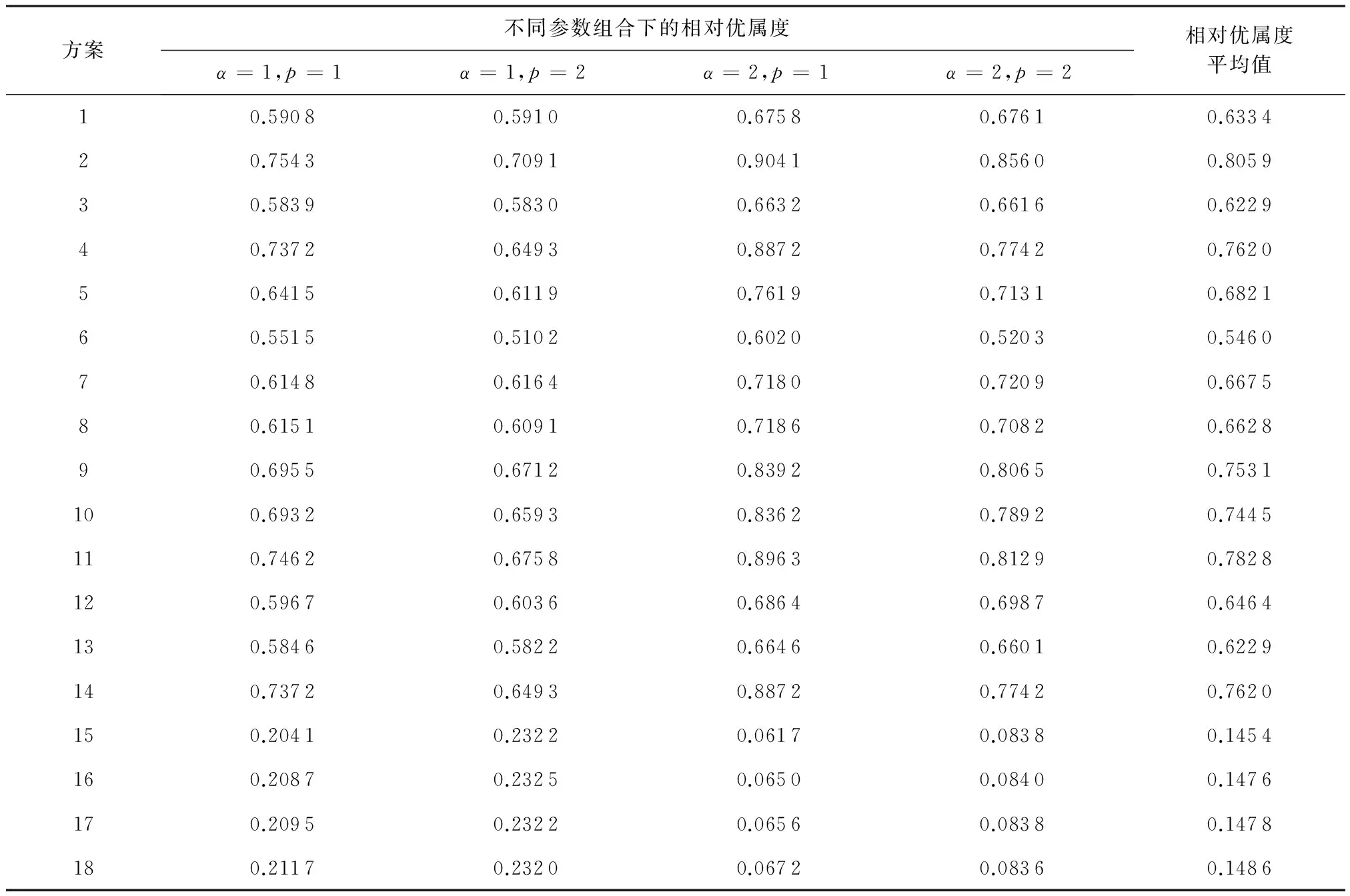
表2 4种优化准则参数和距离参数组合下18个方案的相对优属度及每个方案在4种组合下的相对优属度平均值

当取ωk=(0.288，0.535，0.177)时，18个方案的相对优属度平均值依次为(0.779 2 0.880 3 0.776 5 0.895 7 0.829 2 0.488 5 0.790 3 0.798 6 0.414 1 0.373 5 0.893 8 0.773 1 0.779 1 0.895 7 0.162 0 0.167 7 0.169 2 0.174 7)，模型仿真可以得出方案4或方案14为最优方案。方案4是解以虚拟水最小指标为目标、人均用水公平性差异最小指标为约束的单目标优化模型所得到的方案。而方案14是以虚拟水最小指标为目标、另2个指标为约束的单目标优化模型所得到的方案。与上述分析类似，该方案与方案最初的选定方式相一致。仿真结果也表明模型所得到的方案是综合性能最优的方案。

4 结 语

建立了基于虚拟水及营养学的水资源优化配置问题的多目标优化模型，该模型包括经济效益最大化、虚拟水用水量最小及人均水资源分配公平差异性最小3个目标。模型在考虑虚拟水优化配置的同时，包含了营养均衡等约束条件。给出了解决该模型的多个可行方案，利用可变模糊决策理论从多个方案中选出综合指标最优的方案。以石羊河流域的各地区为例对模型进行了仿真，结果与得到的方案最初的选定方式相符，模型所得到的方案也是综合性能最优的方案。

随着人们生活水平的不断提高，越来越多的人不再仅仅满足于基本的饮食需求，而是要求饮食健康合理。这就要求各地区在生产各类农畜产品时不仅考虑满足虚拟水消耗少，经济效益高，还需要综合考虑营养学因素对生产规划的影响。在某些缺水地区制定规划时，如果对经济效益有着一定的要求，同时虚拟水消耗不能超过某定值，便可利用本文模型得出最佳方案。另外，使用该模型对某地区实际数据进行模拟所得结果，可为管理者在制定地区规划时(如制定该地区的年度GDP预算等)提供参考。

[ 1 ] ALLAN J A.Fortunately there are substitutes for water otherwise our hydro-political futures would be possible[M]. London：ODA，Priorities for Water Resources Allocation and Management，1993：13-26.

[ 2 ] 徐中民，龙爱华，张志强，等.虚拟水的理论方法及在甘肃省的应用[J].地理学报，2003，58(6)：861-869.(XU Zhongmin，LONG Aihua，ZHANG Zhiqiang，et al.Virtual water consumption calculation and analysis of gansu province in 2000[J]. Acta Geographica Sinica，2003，58(6)：861-869. (in Chinese))

[ 3 ] 程国栋.虚拟水：中国水资源安全战略的新思路[J].中国科学院院刊，2003，18(4)：260-265.(CHENG Guodong. Virtual water：a strategic instrument to achieve water security[J].Bulletin of Chinese Academy of Sciences，2003，18(4)：260-265. (in Chinese))

[ 4 ] 杨志峰，支援，尹心安，等.虚拟水研究进展[J].水利水电科技进展，2015，35(5)：181-190.(YANG Zhifeng，ZHI Yuan，YIN Xinan，et al.Research advances in virtual water[J].Advances in Science and Technology of Water Resources，2015，35(5)：181-190. (in Chinese))

[ 5 ] 严冬，周建中，孙怀卫，等.基于虚拟水流动均衡性的农业用水综合调控[J].农业工程学报，2014，30(21)：91-98.(YAN Dong，ZHOU Jianzhong，SUN Huaiwei，et al.Comprehensive regulation of agricultural water based on equilibrium of virtual water flow[J].Transactions of the Chinese Society of Agricultural Engineering，2014，30(21)：91-98. (in Chinese))

[ 6 ] 黄晓荣，裴源生，梁川，等.宁夏虚拟水贸易计算的投入产出方法[J].水科学进展，2005，16(4)：564-568.(HUANG Xiaorong，PEI Yuansheng，LIANG Chuan，et al.Input/output method for calculating the virtual water trading in Ningxia[J].Advances in Water Science，2005，16(4)：564-568. (in Chinese))

[ 7 ] 蔡振华，沈来新，刘俊国，等.基于投入产出方法的甘肃省水足迹及虚拟水贸易研究[J].生态学，2012，32(20)：6481-6488.(CAI Zhenhua，SHEN Laixin，LIU Junguo，et al.Applying input-output analysis method for calculation of water footprint and virtual water trade in Gansu Province[J].Acta Ecologica Sinica，2012，32(20)：6481-6488. (in Chinese))

[ 8 ] 周姣，史安娜.区域虚拟水贸易计算方法及实证[J].中国人口·资源与环境，2008，18(4)：184-188.(ZHOU Jiao，SHI Anna. Method for calculating virtual water trade and demonstration[J].China Population Resources and Environment，2008，18(4)：184-188. (in Chinese))

[ 9 ] 项学敏，周笑白，周集体，等.工业产品虚拟水含量计算方法研究[J].大连理工大学学报，2006，46(2)：179-184.(XIANG Xuemin，ZHOU Xiaobai，ZHOU Jiti，et al. Study of virtual water calculation method of industrial products[J]. Journal of Dalian University of Technology，2006，46(2)：179-184. (in Chinese))

[10] 曹建廷，李原园，张文胜，等.农畜产品虚拟水研究的背景、方法及意义[J].水科学进展，2004，15(6)：829-834.(CAO Jianting，LI Yuanyuan，ZHANG Wensheng，et al.Research background，methodological issues and significance on virtual water of crop and livestock production[J].Advances in Water Science，2004，15(6)：829-834. (in Chinese))

[11] 鲁仕宝，黄强，马凯，等.虚拟水理论及其在粮食安全中的应用[J].农业工程学报，2010，26(5)：59-64.(LU Shibao，HUANG Qiang，MA Kai，et al.Virtual water theory and its application in food security[J].Transactions of the Chinese Society of Agricultural Engineering，2010，26(5)：59-64. (in Chinese))

[12] 杨明智，薛联青，郑刚，等.基于WEAP的叶尔羌河流域水资源优化配置研究[J].河海大学学报(自然科学版)，2013，41(6)：493- 499.(YANG Mingzhi，XUE Lianqing，ZHENG Gang，et al.Optimized allocation of water resources in Yarkand River Basin based on WEAP model[J].Journal of Hohai University (Natural Sciences)，2013，41(6)：493- 499. (in Chinese))

[13] VANHAM D. The water footprint of Austria for different diets [J]. Water Science & Technology 2013，67(4)：824-830.

[14] 陈守煜.工程可变模糊集理论与模型：模糊水文水资源学数学基础[J].大连理工大学学报，2005，45(2)：308-320.(CHEN Shouyu. Theory and model of engineering variable fuzzy setmathematical basis for fuzzy hydrology and water resources[J]. Journal of Dalian University of Technology，2005，45(2)：308-320. (in Chinese))

[15] SU Xiaoling，LI Jianfang，VIJAY P S. Optimal allocation of agricultural water resources based on virtual water subdivision in Shiyang River Basin[J]. Water Resour Manage，2014，28：2243-2257.

Optimizedallocation of water resources based on virtual water and nutrition

ZHANG Binwu1，2，KANG Hongbo2，GUAN Xiucui3

(1.DepartmentofMathematicsandPhysics，HohaiUniversity，ChangzhouCampus，Changzhou213022，China；2.CollegeofInternetofThingsEngineering，HohaiUniversity，Changzhou213022，China；3.DepartmentofMathematics，SoutheastUniversity，Nanjing210096，China)

In order to consider the importance of the economic benefit，virtual water consumption，fairness difference of water use per person，and nutrition factors in the regional planning of production of agricultural and livestock products，the optimized allocation problem of water resources based on the virtual water and nutrition was studied. A multi-objective optimization model with the maximum economic benefit，the minimum fairness difference of water use per person，and the minimum virtual water consumption，meeting the constraints of nutrition factors，was established. The model was solved using the variable fuzzy decision-making theory and an optimal scheme for production of each kind of agricultural and livestock product was obtained. The model was run based on data from the Shiyang River Basin，and the results show that the scheme obtained from the model is the optimal scheme.

virtual water；multi-objective optimization model；nutrition balance；optimal allocation of water resources； fuzzy decision； Shiyang River Basin simulation

10.3876/j.issn.1000-1980.2017.01.005

2016-04-05

国家自然科学基金(11471073，2015B27914)

张斌武(1969—)，男，新疆托里人，教授，博士，主要从事运筹学与控制论研究。E-mail：1312094692@qq.com

TV21

A

1000-1980(2017)01-0030-06