基于VisVSA技术的三维统计公差分析及应用

林 洁，王 佳

（1.同济大学 机械工程学院，上海 200092；2.博世电动工具（中国）有限公司，浙江 310052）

基于VisVSA技术的三维统计公差分析及应用

林 洁1，王 佳2

（1.同济大学 机械工程学院，上海 200092；2.博世电动工具（中国）有限公司，浙江 310052）

圆锯作为一种手持式电动工具，终端客户对其切割精度和切割质量提出越来越高的要求。因此在设计、制造和装配过程中，需要对零部件的尺寸和公差进行详细的分析和控制。使用VisVSA软件建立起了一个圆锯切割精度的数字化公差模型，并采用统计公差的方法对装配过程进行仿真。可以在设计初期预测出偏差的数量和原因，这将有助于提高产品精度，加速研发过程，降低生产成本。

计算机辅助公差；VisVSA；统计公差；圆锯

0 背景和问题

圆锯是一种通过锯片的旋转运动来切割木材、金属等材料的手持式电动工具。无论是做90°切割还是45°斜切，圆锯配合导轨使用都是保证精度和直线度的最简单的方法[1]，如图1所示。这样可以减少后续的加工工序，确保相配的工件可以正确连接。配合导轨使用时，锯片切割线与导轨滑槽之间的平行度直接影响到切割是否平顺和被加工材料的表面质量，如图2所示。

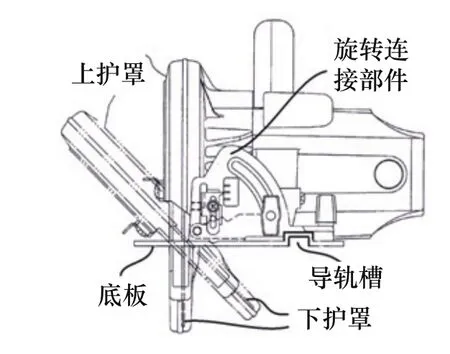
图1 圆锯角度调整原理

图2 锯片切割线与导轨滑槽之间的平行度

因此在圆锯设计中，知道尺寸链中各个组成环对锯片切割线与导轨滑槽之间的平行度有多大影响是一个重要的问题。以往设计人员多是凭借经验进行公差分配，在批量生产之后才有可能判断出公差设计是否合理。这个过程常常需要反复进行，既拖延了生产周期又使成本增加。而采用计算机辅助公差分析软件VisVSA可以有效地解决这个问题。

1 公差链的组成

在一个典型的圆锯中，从导轨滑槽到锯片之间有底板、旋转连接部件、上护罩、轴承座、轴承、传动轴和定位垫圈等零部件，如图3所示。锯片通过传动系统与上护罩相连，上护罩又通过一套旋转定位机构连接到底板上，以实现精确调节切割深度和切割角度的目的。

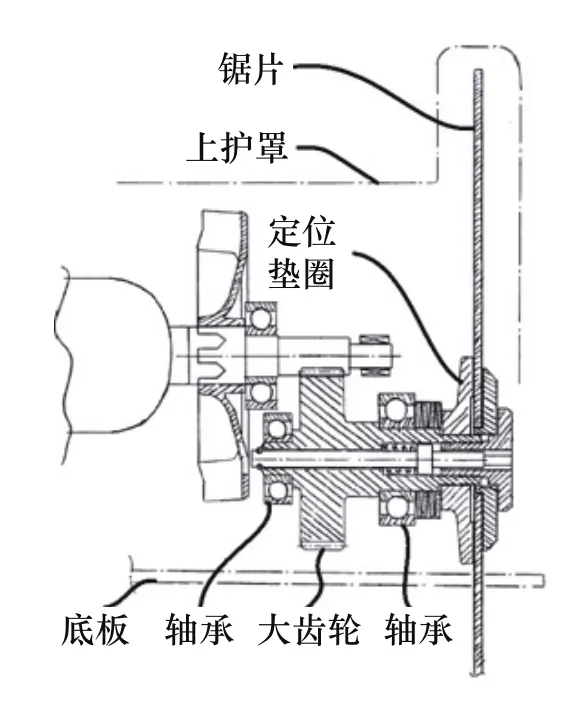
图3 导轨和锯片之间的装配尺寸链

图4 上护罩关键几何特征的尺寸公差

为了能够在所有旋转角度及调整高度的状态下，底板与导轨都可以正常配合使用，就要求锯片的斜切旋转轴线一直位于工件的切割线上。为实现这些要求，底板与上护罩之间的旋转部件中有许多复杂的结构特征并标注了大量的几何公差。锯片通过定位垫圈、传动轴及轴承连接到上护罩上，上护罩本身包含了轴承座的位置度、安装孔的位置度、深度调节面的平面度等许多三维公差，如图4所示。

由上述例子可见，尺寸链是由很多组成环构成，这些组成环并不在一条直线或者一个平面上，而是空间布局的三维公差。对于较长的尺寸链来说，传统的极限公差模型不能反映实际情况，其主要缺点在于对单个组成环的公差要求很高，从而带来昂贵的制造成本、复杂的检测流程和较高的零件废品率。而统计公差模型则可以在不牺牲质量的前提下放宽组成环公差[2]。

2 公差模型的建立

2.1 VisVSA简介

VisVSA是Siemens公司开发的一套三维统计公差软件，它基于Monte Carlo方法，主要用于三维统计公差分析。VisVSA是一个强大的公差分析工具，用来对制造和装配过程进行仿真，并可以对偏差的数量和原因进行预测。其中的数字样机可以用来全面地表现几何特征、产品偏差、装配过程偏差（装配次序、组件连接的定义、工装等）以及测量要素。不需要制造出任何实物零件或者模具，使用数字样机便可以预测装配过程中可能出现的问题[3]。

Monte Carlo方法是VisVSA公差分析的理论基础。VisVSA中公差分析的基本原理是在组成环公差范围内按照设定的概率分布生成一系列随机数，然后对其随机抽样，代入尺寸链方程即可求解出封闭环的一个样本值。然后按照一定的置信水平设定的次数重复这个过程，从而得到封闭环的样本集合。最后对封闭环样本集进行统计处理便可得到封闭环尺寸的公差信息。Monte Carlo仿真对系统的复杂性不敏感，计算时间并不会因为系统变量的增多而有显著增加[4]。

2.2 导入3D模型

导入VisVSA的3D模型需要是JT格式。这是一种广泛应用在产品设计中有关产品可视化的公开的三维数据格式，它的特点是能在保留模型细节特征的同时维持比较小的文件体积。常用的CAD建模软件如Pro/ E等都有相应的插件可以输出为JT格式。在VisVSA中进行公差分析首先需要新建一个过程文件（Process Document），然后便可将其与对应的JT文件关联起来。

2.3 建立公差模型，进行数字样机的装配仿真

VisVSA公差模型是基于零件几何特征建立的，常用的特征有孔（Hole）、轴（Shaft）、槽（Slot）、肋板（Tab）和平面（Plane）等。在这些特征上以及特征之间可以标注几何尺寸和公差，并建立零件之间的装配关系。例如孔和轴、槽和肋板可以分别形成一对装配特征。完成装配之后，可以定义测量关系。在本例中我们选择测量锯片切割线和底板导轨滑槽之间的夹角（前述平行度）来衡量整个装配链对切割精度的影响。

在VisVSA中每个特征的公差都可以根据实际需要定义它的分布，比如正态分布、均匀分布等。零件之间的连接关系也有多种选项供选择，比如轴和孔就有相切、浮动、平行、重合等空间位置关系。这些特征、公差和装配关系共同组成了一个数字样机模型。然后按照Monte Carlo方法在定义的公差范围内随机生成带有不同偏差的数字样机模型，并模拟实际装配。这样在很短时间内即可通过仿真大量模型来获取期望的测量值。本例的圆锯公差模型在普通配置电脑上模拟装配2000次数字样机，只需要大概几分钟时间。

2.4 仿真结果

VisVSA可以给出测量结果的分布情况，如图5所示。根据中心极限定理，在尺寸链较长的时候测量结果（即封闭环）非常接近于正态分布[5]。仿真的结果包括均值、±3σ的数值以及过程控制指数Cp等。图5是某一次仿真的结果，其中设计要求的切割精度180±0.3°（USL和LSL）外侧为不合格区域。不合格比例较大时设计人员可以反复调整组成环公差，并多次运行仿真直到符合要求。仿真时如果采取High-Low-Medium选项，也可以给出极限公差的结果。极限公差的上下限范围一般会远大于设计要求的切割精度范围，而在实际当中接近上下限的情况却很少出现。如果依据极限公差设计切割精度，将对加工和装配工艺有极高的要求，这必然带来很大的成本压力，甚至现有工艺无法满足设计精度。而采用统计公差方法，虽然理论上会有少量不合格产品，但在整体上却可以采用较低的公差等级，可显著降低成本。

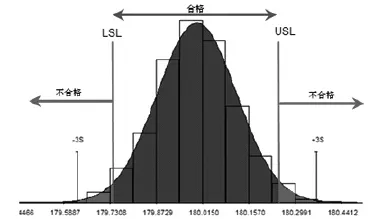
图5 锯片切割线和导轨滑槽之间夹角的分布范围

除此之外，更有用的是VisVSA还可以给出各个尺寸链组成环对最终测量结果的贡献度大小。如图6所示，在贡献度列表中有几十个产生影响的组成环公差，并给出了对应的贡献度百分比。贡献度列表中排列靠前的公差属于关键公差，在这个例子中，定位垫圈的端面全跳动、上护罩轴承孔的位置度和垂直度、传动轴的全跳动等对切割精度有较大的影响。对这几个关键公差进行严格控制，就可以显著提高切割精度。另一方面，可以将表格中后面很多贡献度很小的非关键公差适当放宽，这样并不会影响到最终的切割精度，却可以大大节省生产成本。

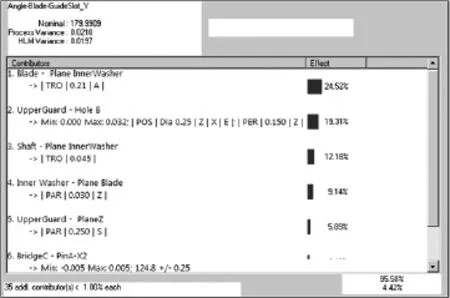
图6 尺寸链各组成环的贡献度

3 结论

将VisVSA中的公差分析方法应用到电动工具行业是一次新的尝试。圆锯中这条切割精度的尺寸链包含了上百个组成环，只有采用统计公差方法结合计算机技术，才可能得到比较真实的公差分析结果，用于指导设计和生产。本文建立了圆锯的公差模型，可以筛选出影响切割精度的关键组成环。在产品开发的初期便可以据此控制好关键尺寸公差以保证质量，并适当放宽非关键尺寸公差以降低成本。

[1] Circular Saw Guide Rail[EB/OL].http://www.toolstop.co.uk/whyhow-to-use-a-circular-saw-and-a-guide-rail-a1211.

[2] Tolerance Analysis[EB/OL].http://en.wikipedia.org/wiki/ Tolerance_analysis.

[3] Variation Analysis[EB/OL].http://www.plm.automation.siemens. com/en_us/products/tecnomatix/manufacturing-planning/ dimensional-quality/variation-analysis.shtml.

[4] Monte Carlo method[EB/OL].http://en.wikipedia.org/wiki/Monte_ Carlo_method.

[5] Fritz Scholz,Tolerance Stack Analysis Methods[Z].1995.

3D statistical tolerance analysis and application based on VisVSA

LIN Jie1, WANG Jia2

TH124

：A

1009-0134(2017)01-0099-03

2014-07-24

林洁（1984 -），女，浙江人，工程师，本科，研究方向为计算机模拟产品三维统计公差计算及优化。