水平受荷嵌岩桩承载性能的修正模型研究
2017-02-10张坤勇杜伟李广山夏璐刘子剑
张坤勇,杜伟,李广山,夏璐,刘子剑
(1.河海大学岩土力学与堤坝工程教育部重点实验室,江苏 南京 210098;2.江苏省岩土工程技术工程研究中心,河海大学,江苏 南京 210098;3.陕西省交通规划设计研究院,陕西 西安 710065;4.中国公路工程咨询集团有限公司,北京 100097)
水平受荷嵌岩桩承载性能的修正模型研究
张坤勇1,2,杜伟1,2,李广山1,2,夏璐3,刘子剑4
(1.河海大学岩土力学与堤坝工程教育部重点实验室,江苏 南京 210098;2.江苏省岩土工程技术工程研究中心,河海大学,江苏 南京 210098;3.陕西省交通规划设计研究院,陕西 西安 710065;4.中国公路工程咨询集团有限公司,北京 100097)
基于5组大直径嵌岩桩水平受荷现场试验及荷载-位移图,确定p-y双曲线函数法作为文章一系列荷载试验的水平承载力判别准则,从而确定试桩的极限水平承载力。采用Zhang法、Kulhawy法、Reese法三种水平承载力计算理论对荷载试验的水平承载力进行计算,将计算结果和准则判别的真实承载力比较。结果表明,Kulhawy法的解答更适合计算嵌岩桩的水平承载力。修正了Kulhawy计算模型,对系列试验再次进行了修正计算,对上述几类模型的计算结果进行误差分析与比较。结果表明,修正的Kulhawy计算模型解答更接近水平荷载试验的真实承载力值。
嵌岩桩;水平荷载;水平承载力;修正计算模型;现场试验
0 引言
在大型港口工程、海洋结构工程和跨海大桥等近海工程与岩质边坡抗滑工程等基础工程中,以承受水平荷载为主的大型嵌岩桩日益得到越来越广泛的应用。目前国内外对于嵌岩桩的研究已经不少,但是大都局限于竖向荷载作用下的荷载传递机理、承载变形能力及桩端破坏模式,对于大直径嵌岩桩承受水平荷载作用时的受力机理与工作性能研究较少。在实际工程应用中,承受水平向荷载作用下基桩的工作机制不同于竖向荷载作用下的工作机制,水平承载力的计算也会对桩基的设计起关键作用[1]。因此,大型嵌岩桩的水平承载力研究已成为工程建设中的重要研究课题,具有较强的理论研究意义和工程实用价值。
劳卫康等[2]和王建华等[3]通过水平承载力的现场试验结合数值分析研究了水平荷载作用下大直径嵌岩桩的工作机理,根据桩身内力与变形的测试结果分析了大直径嵌岩桩的水平承载特性和桩岩相互作用性状,从而总结出桩-岩共同作用的规律。祝廷尉等[4]进行了嵌岩桩与滑坡体相互作用的物理模型试验,分别研究滑坡推力作用下模型桩的受力特征、桩身弯矩分布规律及模型变形破坏模式,分析了嵌岩桩在加固滑坡中的抗滑特性和桩土相互作用机制。本文通过大直径水平受荷嵌岩桩的现场试验,确定p-y双曲线函数法作为本文一系列荷载试验的判别准则,利用三种常用的嵌岩桩水平承载力计算理论对荷载试验的水平承载力进行计算,并与准则判别结果进行比较与评价,最终修正确定了一种比较合理的水平受荷嵌岩桩的水平承载力计算方法。
1 试验概况
1.1 试验布置
本文涉及到的5组试验[5]分别设置2根直径均为0.762 m的长短嵌岩桩,采用美国北卡州交通部的试验框架对长短两桩同时施加水平向荷载。在桩内加强筋上附着测斜仪,用于观测桩的变形;在桩身布置应变计,用于记录桩在受荷时的应变。
1.2 加载方法
在本试验中,液压千斤顶所施加的水平向荷载增量在45~90 kN之间,加荷后再卸荷,直到桩顶没有明显的位移(<0.127 mm/h),停止施加该级荷载。
1.3 试验岩体特性
在试桩的位置进行表面钻孔取芯,检查所有的岩芯试样,选择试样用于室内试验,5组试验桩的几何尺寸、荷载参数及岩体参数见表1。
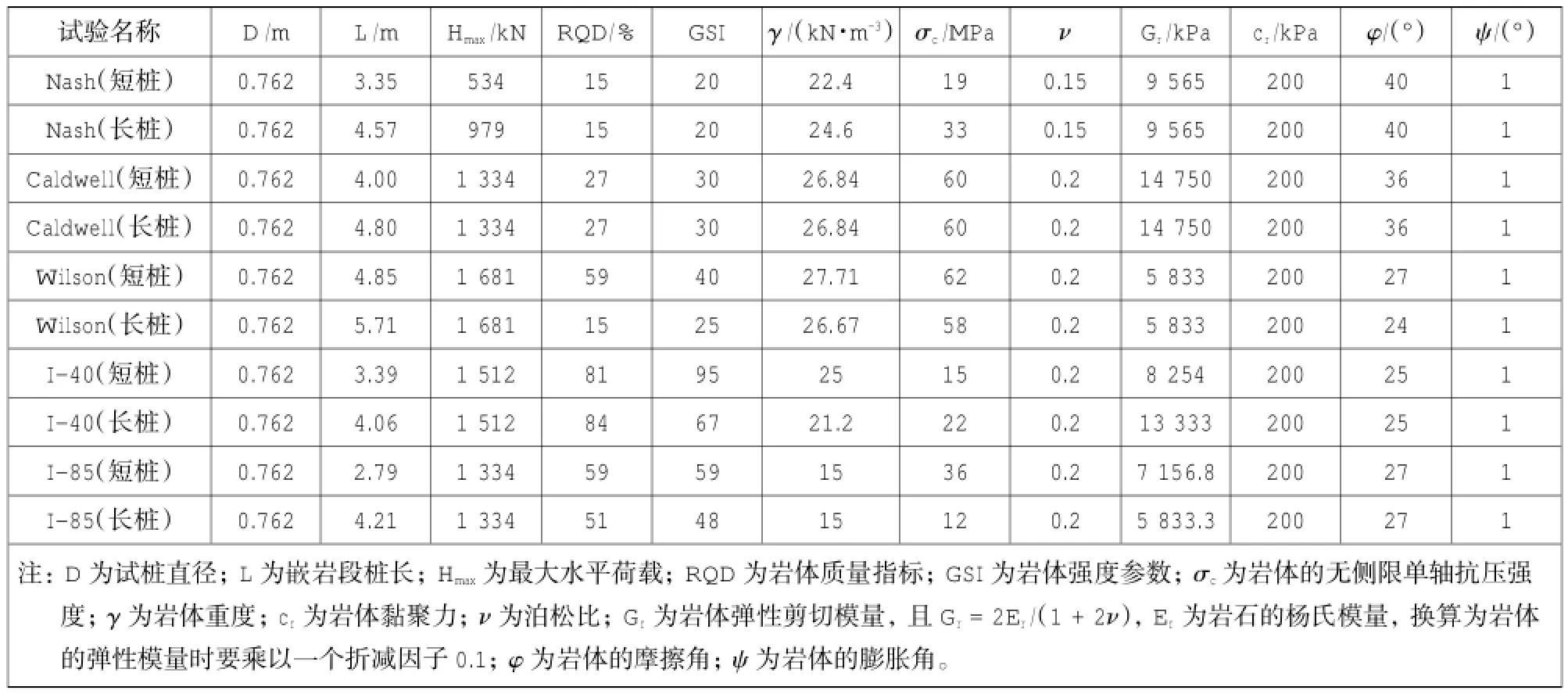
表1 水平载荷试验桩的荷载参数及岩体参数Table 1 Loads and rock parameters of test piles under lateral loading
2 试验分析
2.1 试验结果
在Nash试验中,施加的水平荷载达到534 kN后,短桩的水平位移达到0.135 m,短桩破坏后,在它的后面安装一个混凝土块来增加它的额外抗力,继续施加荷载达979 kN,长桩仍没有达到它的极限阻力。Caldwell试验中施加最大荷载至1 334 kN时,短桩水平向位移为0.089 m,长桩水平位移为0.023 m。Wilson试验中施加至荷载框架所能承受的最大荷载1 681 kN时,短桩水平位移为0.034 m,长桩的水平位移为0.055 m。I-40试验中施加增量为89 kN的水平向荷载至最大荷载1 512 kN时,短桩的水平位移为0.011 3 m,长桩的水平位移为0.016 1 m。试验结果见表2。
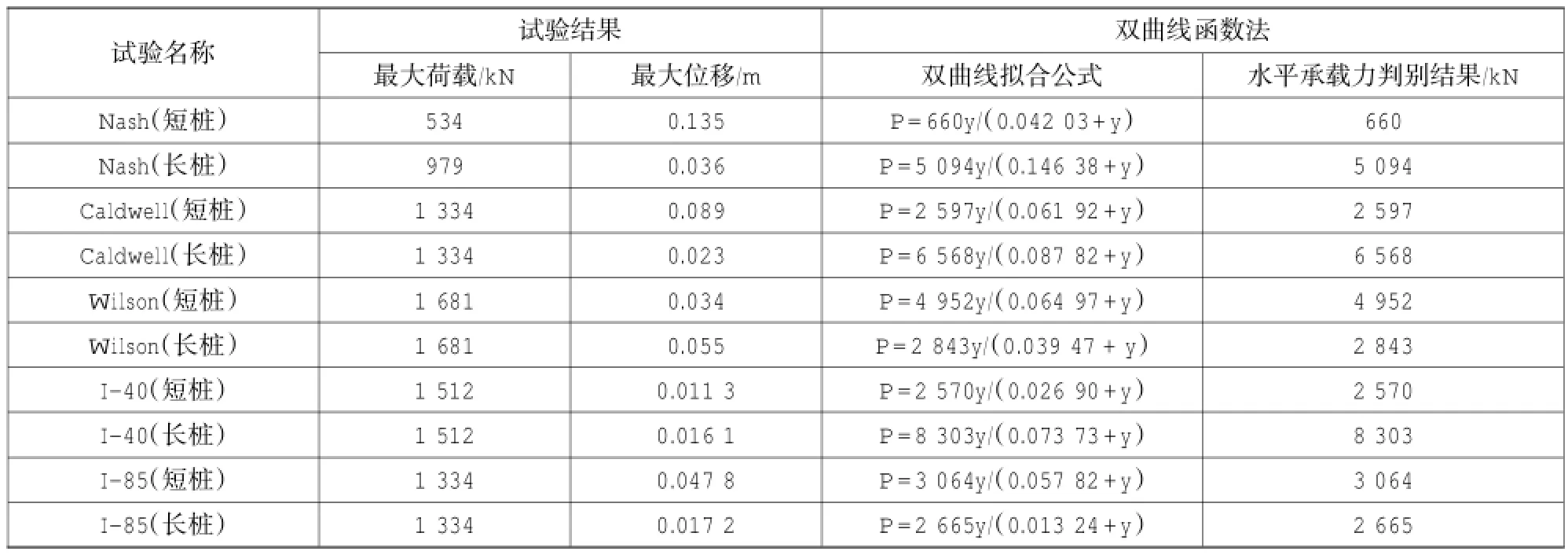
表2 嵌岩桩水平承载力判别结果Table 2 Discriminant results of horizontal bearing capacity of rock-socketed piles
2.2 水平承载力判别准则
基于有限元分析,再加上实验室测试及现场水平荷载试验的综合结果,Gabr[5]在2002年基于风化岩石条件下发展了p-y双曲线函数法。对于所提出的双曲线函数,地基模量kh和极限反力pult是两个必需的参数。kh表示p-y曲线的初始切线模量,通过现场的测量值进行倒算。由于在实际应用中不可能有足够大的变形来发展极限反力,所以往往通过拟合曲线外推的办法来估计极限反力pult。函数形式如式(1)所示:

式中:a=1/kh;b=1/pult,pult是水平向极限反力;p为承载力,kN;y为桩体的水平向位移,m。本文对各组试验数据进行拟合,得到双曲线形式方程:

那么pult=p1,这点在物理意义上是符合条件的。
基于双曲线函数法,对5组试验的长短两根嵌岩桩进行水平承载力判别,将试验过程中荷载-位移曲线进行拟合,所得双曲线函数与准则判别结果汇总于表2。
可以看出,根据双曲线函数法所判别出的承载力大于试验得到的最大荷载,在实际试验中,嵌岩桩水平方向达到最大荷载时,依然没有进入屈服状态,故真实的极限承载力应该大于试桩的最大荷载。基于以上分析,确定双曲线函数法作为本文一系列荷载试验的水平承载力判别准则,且根据双曲线函数法判别的嵌岩桩承载力视为试桩的真实承载力。下文将利用相关嵌岩桩的水平承载力计算理论,对5组试验重新计算,并与此真实承载力比较,以寻找和验证合适的计算理论。
3 嵌岩桩的水平承载力计算
3.1 基于Hoek-Brown岩石强度准则的Zhang的解答
Zhang[6]采用了Briaud、Kulhawy[7]假定的反力分布和Hoek-Brown的岩石强度准则[8],假定岩体的总阻力包括两个方面:侧面阻力和极限正应力,给出估计极限阻力的建议方程:

式中:pL为极限正应力;τmax为轴向压缩下的桩单元侧向最大应力。
τmax值按照下式给出:
平滑接触:τmax=0.20(σc)0.5(4)
粗糙接触:τmax=0.80(σc)0.5(5)
式中:σc为岩体的无侧限单轴抗压强度,MPa。
为确定常限应力pL,采用Hoek和Brown发展的岩体强度准则。对于完整岩石,Hoek-Brown准则按照下列形式给出:
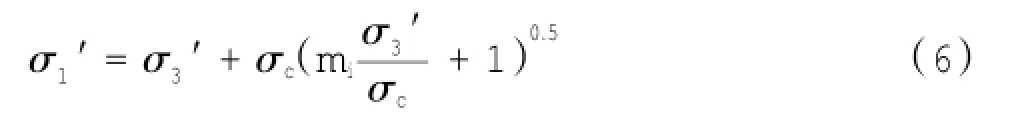
式中:σ1′和σ3′分别是有效的大、小主应力;mi为完整岩石的材料常数。
对于有节理的岩石,Hoek-Brown准则按照式(7)给出:
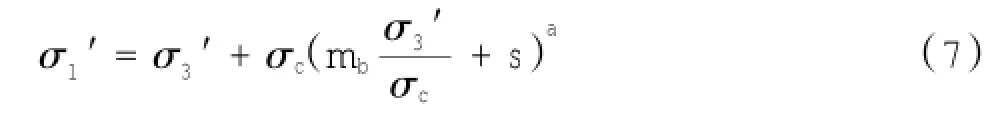
式中:mb、s、a是依赖于岩体特性的常量。
Hoek和Brown[9]假定小的有效主应力σ3′是有效覆盖地层压力γ′z;极限正应力pL是大主应力σ1′。于是有:
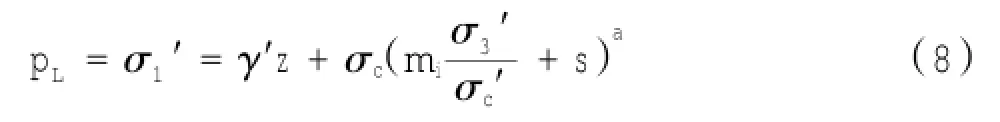
式中:γ′为岩体的有效重度;z为岩体表面以下的深度。
从Zhang的解答方法可以看出:作为嵌岩桩水平承载力的两个来源之一,极限正应力pL的取值主要考虑了地质强度参数GSI、无侧限抗压强度和有效重度。
3.2 Kulhawy解答
Kulhawy[10]首先给出了涉及短粗的刚性嵌岩桩算例的解答,其后发展到了在上覆土层条件下的受水平向荷载嵌岩桩的更多算例的解答。其优点在于能够克服基于Mindlin方程的解答的缺陷,如Poulos模型的解答不能够运用于非均匀成层介质。
桩的极限阻力如式(9)所示:
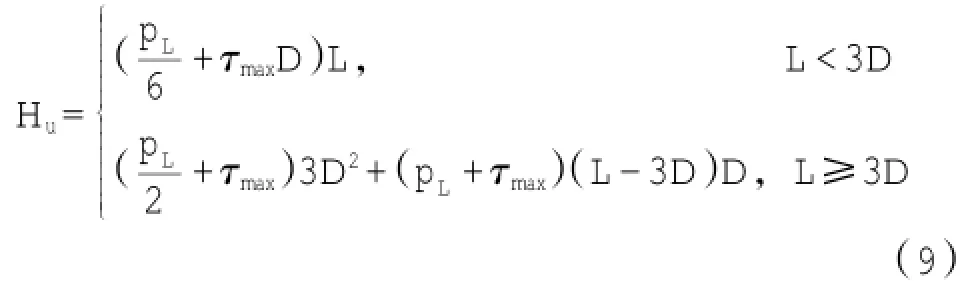
式中:Hu为单元长度的极限应力。
Kulhawy等人在研究置于弹塑性、黏聚-摩擦型膨胀材料中的长圆柱形腔室的膨胀理论过程中,提出了极限应力pL的闭合解析解答。从无量纲量ρ的参数方程可确定极限应力pL,表达式如下:
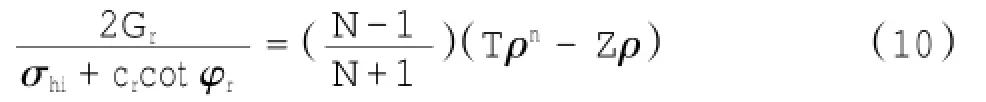
式中:σhi为初始原位水平应力;νr为泊松比;cr为黏聚力;φr为摩擦角;Ψr为完整岩体的膨胀角。
根据Kulhawy对大量实例的研究,τmax的解法按照经验公式(12)给出:

式中:t为无量纲因子。
3.3 Reese解答
基于两个软岩中的水平荷载试验,Reese[11]建立软弱岩石的p-y曲线,存在于软弱岩石表面附近的裂缝可能被土体填充着。基于极限平衡状态,软弱岩石的极限阻力pur的计算用式(13)表示:
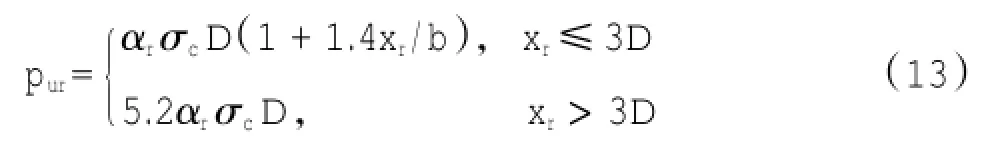
式中:αr为强度折减系数,与岩体质量参数RQD
相关;xr为岩体表面以下的深度。
3.4 计算结果分析
基于5组试验资料,根据以上介绍的3种解答方法,分别对试验的长短嵌岩桩的水平承载力进行计算,并与试验真实承载力作比较,计算结果见表3。
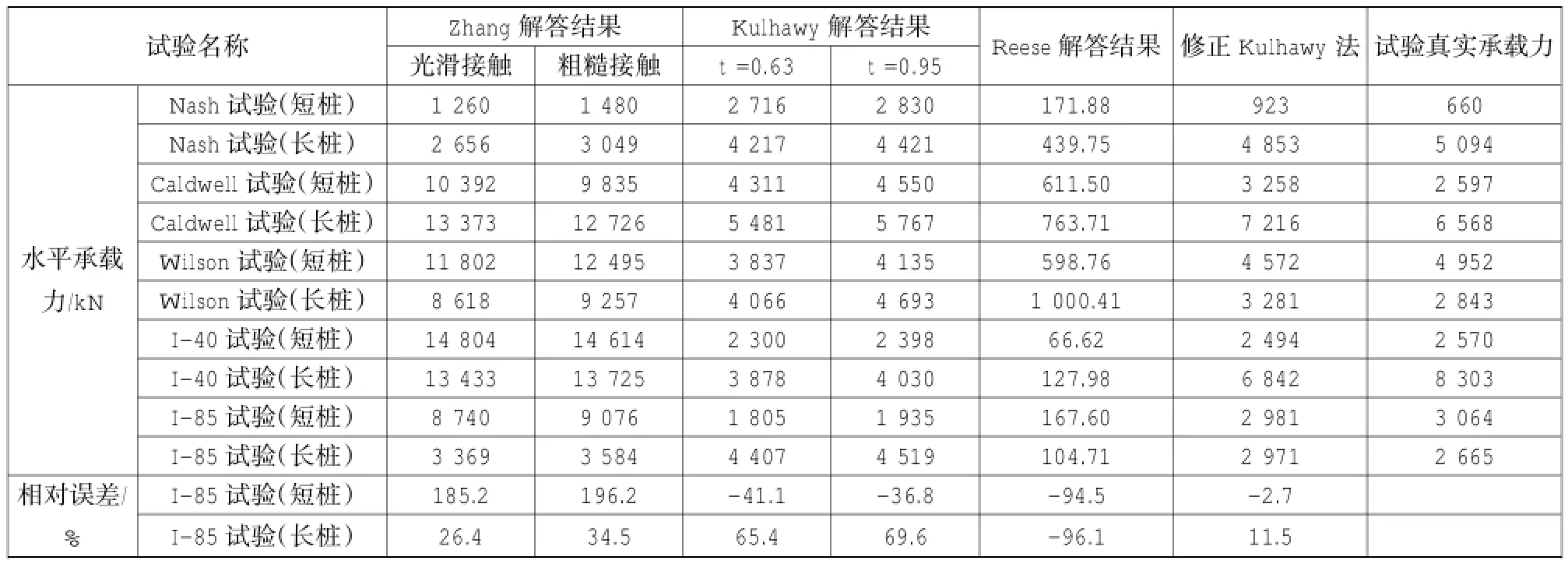
表3 嵌岩桩水平承载力计算结果及I-85试验桩的水平承载力误差分析Table 3 Calculation results of horizontal bearing capacity of rock-socketed piles and error analysis on I-85 test pile
1)除了Nash这组试验外,Zhang法的解答结果均远大于试验真实承载力。然而通过大量试算本文中一系列试验的水平承载力,反映出:Zhang法的解答结果对地质强度指数GSI非常的敏感,水平承载力随着GSI的增大而明显增大;而对反映岩体强度指标的有效重度和无侧限抗压强度则不是很敏感,恰恰Nash这组试验的地质强度指数GSI非常小,这就解释了用Zhang法计算的Nash试验组承载力为什么小于试验的真实承载力,同时也暴露出了Zhang法应用在本文中一系列试验所存在的缺陷。
2)Reese方法的解答结果不仅远小于其他两种方法的计算结果,而且也小于试验所给的最大处的最大荷载,而在撇开Nash试验组的短桩以外,其他的试桩在达到这个最大荷载之前,并没有达到屈服状态,故Reese方法的解答无法反映真实的试验过程。鉴于Reese解答方法的诸多缺陷以及现有的真实试验承载力判别结果,说明该法不适合计算嵌岩桩的水平承载力。
3)相比较前述两种解答方法,Kulhawy解答方法考虑了更为广泛的影响岩体强度因素,包括摩擦角、岩体膨胀角、黏聚力等诸多因素。而且,Kulhawy法的解答结果较接近于试验的真实承载力。因此该法的计算结果更为客观和真实。
基于以上与真实试验承载力的比较分析,可以得出初步结论:Kulhawy法的解答适合计算嵌岩桩的水平承载力。
4 修正Kulhawy计算模型
为了最大程度地减小误差,使得该解答方法的计算结果更接近试验真实承载力,对Kulhawy法计算模型进行修正,并用修正后的计算模型对现场荷载试验进行验算。为了方便修改τmax和pL的表达式,引入两个新的变量τmaxA和pLB。结合公式(12),分别建立τmax与σc的关系、pLB与pL的关系:

式中:A、B均为常数。
为了确定待定系数A和B,选取两个试验为Nash长桩和I-40短桩试验的真实承载力,并联立方程:
Nash长桩:
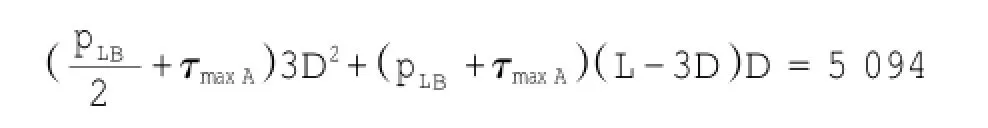
I-40短桩:
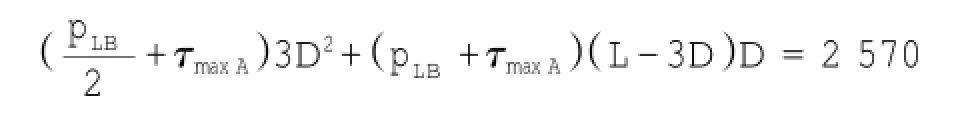
同时结合式(14)、式(15),求得:A=6.163,B=0.316,满足条件。因此修正的Kulhawy计算模型为:
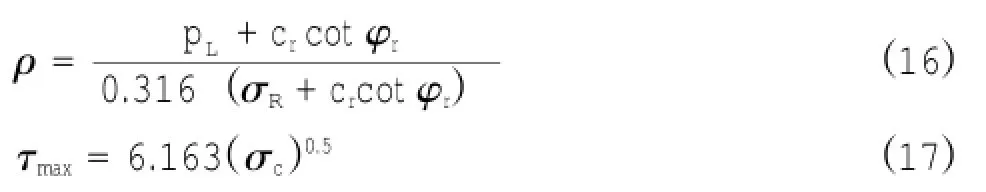
为了验证修正的Kulhawy计算模型的合理性与相对准确性,分别用修正前与修正后的Kulhawy计算模型以及Zhang法和Reese法对各试验的长短嵌岩桩进行水平承载力计算,然后将它们的计算结果与试验真实承载力进行比较并计算相对误差。
如表3所示,修正Kulhawy计算模型计算典型荷载试验的相对误差远远小于其他几类方法的计算结果,且其计算长桩的相对误差11.5%和短桩的相对误差2.7%也属于可控范围,与真实承载力吻合良好,可见修正Kulhawy计算模型更适合计算嵌岩桩的水平承载力。
5 结语
1) 根据p-y双曲线函数法建立本文嵌岩试桩的水平承载力判别准则,并将双曲线函数法判别的嵌岩桩承载力作为试桩真实的承载力极限值。
2)介绍了Kulhawy法、Zhang法、Reese法这3种水平承载力计算理论及其相应的计算公式。基于荷载试验资料所给定的参数,运用上述3种计算理论分别对5组嵌岩试桩进行水平承载力计算,将每种方法的计算结果与双曲线函数法的判别结果进行比较,发现后两种方法的偏差很大,因而选定偏差相对较小的Kulhawy解答方法作为本文一系列嵌岩桩试验的水平承载力计算方法。
3)鉴于Kulhawy解答方法的计算结果和判别准则结果的偏差还是比较明显的,分析两者存在偏差的原因,对原Kulhawy计算模型进行修改,调整了原计算公式中的局部参数,以便和判别准则结果达到最大程度的吻合,形成了修改后的Kulhawy计算模型。
4)为了验证前述修改计算模型的适用性,通过4种计算方法与水平承载力判断准则计算结果的误差分析,确定了修正Kulhawy计算模型的有效性,从而为相关设计者们提供了设计参考。
[1]YANG K,LIANG R.Lateral response of large diameter drilled shafts in clay[C]//Proceedings of DFI 30th annual conference on deep foundations.Chicago:Deep Foundations Institute,2002.
[2]劳伟康,周立运,王钊.大直径柔性钢管嵌岩桩水平承载力试验与理论分析[J].岩石力学与工程学报,2004,23(10):1 770-1 777. LAO Wei-kang,ZHOU Li-yun,WANG Zhao.Field test and theoretical analysis on flexible large-diameter rock-socketed steel pipe piles under lateral load[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(10):1 770-1 777.
[3]王建华,陈锦剑,柯学.水平荷载下大直径嵌岩桩的承载力特性研究[J].岩土工程学报,2007,29(8):1 194-1 198. WANG Jian-hua,CHEN Jin-jian,KE Xue.Characteristics of large diameter rock-socketed piles underlateral loads[J].Chinese Journal of Geotechnical Engineering,2007,29(8):1 194-1 198.
[4]祝廷尉,胡新丽,徐聪,等.嵌岩桩抗滑特性的物理模型试验研究[J].岩土力学,2014,35(S1):165-172. ZHU Ting-wei,HU Xin-li,XU Cong,et al.Physical model test research on anti-sliding characteristics of rock-socketed pile[J]. Rock and Soil Mechanics,2014,35(S1):165-172.
[5]GABR M A,BORDEN R H,CHO K H,et al.P-y curves for laterally loaded drilled shafts embedded in weathered rock[M].Raleigh: Department of Civil Engineering of North Carolina State University,2002.
[6]ZHANG L,EINSTEIN H H.Analysis and design of drilled shafts in rock[R].Massachusetts Institute of Technology,1999.
[7]KUIHAWYF H,CARTERJ P.Socketedfoundationsinrock masses [J].Engineering in Rock Masses,1992:509-529.
[8]HOEK E,BROWN E T.Empirical strength criterion for rock masses [J].Journal of the Geotechnical Engineering Division,1980,106 (9):1 013-1 035.
[9]HOEK E,BROWN E T.Practical estimates of rock mass strength [J].International Journal of Rock Mechanics&Mining Sciences,1997,34(8):1 165-1 186.
[10]CARTER J P,KULHAWY F H.Analysis of laterally loaded shafts in rock[J].Journal of Geotechnical Engineering,1992,118(6): 839-855.
[11]REESE L C.Analysis of laterally loaded piles in weak rock[J]. Journal of Geotechnical&Geoenvironmental Engineering,1997, 123(11):1 010-1 017.
Model modification on horizontal bearing capacity performance of rock-socketed piles under lateral loads
ZHANG Kun-yong1,2,DU Wei1,2,LI Guang-shan1,2,XIA Lu3,LIU Zi-jian4
(1.Key Laboratory of Ministry of Education for Geomechanics and Embankment Engineering,Hohai University,Nanjing, Jiangsu 210098,China;2.Jiangsu Research Center for Geotechnical Engineering Technology,Hohai University,Nanjing, Jiangsu 210098,China;3.Shaanxi Provincial Transport Planning Design and Research Institute,Xi′an,Shaanxi 710065,China; 4.China Highway Engineering Consulting Corporation,Beijing 100097,China)
Based on the in-situ tests for 5 groups of big-diameter rock-socketed piles under lateral load and the loaddeflection curves,we determined the p-y hyperbolic function method as the horizontal bearing capacity criterion of a series of the load tests,and determined the ultimate bearing capacities of test piles.According to different calculation theories of horizontal bearing capacity,such as Zhang method,Kulhawy method and Reese method,we calculated the horizontal bearing capacities of load tests,and compared with the true bearing capacity analyzed by the criterion.The results show that the Kulhawy method is more suitable for calculating horizontal bearing capacity of rock-socketed piles.The Kulhawy calculation model was modified and the modified calculation model was verified with these load test parameters.Error analysis of these methods was given and a comparison was made.The results show that the calculation results of the modified Kulhawy calculation model are closer to the true values of horizontal bearing capacity.
rock-socketed pile;lateral load;horizontal bearing capacity;modified calculation model;in-situ test
TU473.11
A
2095-7874(2017)01-0024-05
10.7640/zggwjs201701005
2016-07-02
2016-08-30
国家自然科学基金重点项目(41530637);中央高校基本科研业务费专项资金项目(2015B17714)
张坤勇(1975— ),男,安徽濉溪人,副教授,工学博士,岩土工程专业。E-mail:ky_zhang@hhu.edu.cn
