砂岩泊松比函数的提出及研究

田家林，吴波，伍开松，赵攀

（1.西南石油大学机电工程学院，四川 成都 610500；2.西南交通大学机械工程学院，四川 成都 610031）

砂岩泊松比函数的提出及研究

田家林1，2，吴波1，伍开松1，赵攀1

（1.西南石油大学机电工程学院，四川 成都 610500；2.西南交通大学机械工程学院，四川 成都 610031）

泊松比是一个重要的材料属性参数，它反映了材料在受载情况下横向变形和纵向变形之比，有明确的物理意义。但岩石的泊松比相对金属而言有其特殊性，岩石的泊松比不是定值，而金属的泊松比是定值，故岩石泊松比的变化规律值得深入研究。文中以南充砂岩和武胜砂岩2种岩样为例进行了岩石三轴压缩实验，分析处理了实验数据，提出了泊松比函数概念，并且推导出了泊松比函数公式，得到了泊松比函数与标准泊松比、峰值泊松比以及最大泊松比之间的关系，分析了泊松比函数中的各个材料参数的物理意义。泊松比函数很好地解释了岩石在受力变形过程中的一些物理现象，具有实际的力学研究意义。

弹性常数；三轴压缩实验；泊松比函数；标准泊松比

0 引言

岩石力学参数研究是岩石工程的一个重要课题，可为岩石质量评价、破坏方式、类型性质判别，以及岩体或建筑物稳定性分析提供不可或缺的基础数据［1］。泊松比是材料属性参数中一个非常重要的弹性常量，自从其概念提出后，很快就被广泛应用于力学中了。S.D. Poisson［2］1829年在自己的回忆录中，首次提出了弹性常数1/4可以作为泊松比的预测值。R.S.Lakes［3］1987年制备出了泊松比为-0.7的聚氨酯泡沫，泊松比材料的研究进入一个快速发展的阶段。K.E.Evan等［4］进一步总结了具有负泊松比的材料和结构。

后来，泊松比被引进到了岩石力学研究之中。国际岩石力学学会定义的泊松比是在比例极限范围内材料的横向变形和纵向变形之比，但在比例极限范围内研究岩石泊松比很受限制，因此，许多学者［5-9］对其进行了扩展，用以研究岩石的损伤、破裂和断裂。Q.Wang等［10］发现了泊松比和围压之间的关系，并且利用激光脉冲间接测量得出了围压状态下的泊松比，推导得出了标准泊松比和围压之间的函数关系。他们发现泊松比在200 MPa围压下是一个逐渐增大的值，大于200 MPa时几乎是个定值；但并没有深入研究不同围压状态下除比例极限之外岩石各变形阶段的泊松比。刘斌等［11］也利用类似的方法对不同围压下岩石泊松比的各向异性进行研究。王学滨［12］对岩样单轴压缩峰值后泊松比理论进行了研究，首次接触到了除比例极限外的泊松比，但也并未深入研究下去。

潘华等［13］对原状海洋土动泊松比进行了循环三轴及循环扭剪实验，得到土体固结围压和固结应力比对动泊松比的影响，但并未对土体各个受力变形阶段泊松比的变化规律进行深入研究，仅仅探讨了不同剪切应变下的泊松比变化规律。黄兴建等［14］对粉砂质泥岩和泥质粉砂岩进行了三轴循环载荷实验，发现在围压很低的情况下，动泊松比与动压力有一定关系，但是同样没有考虑岩石受力变形的整个阶段。C.W.Smith等［15］依据实验数据解释了高度非线性材料的泊松比，提出用泊松比函数解释拉胀材料出现泊松比负值的现象，指出波动比函数是材料瞬时行为的一种度量方法，但研究的材料仅限于受轴向载荷的情况，有一定局限性。

为了更好地研究岩石在实际受载变形全程中的泊松比变化规律，本文利用南充砂岩和武胜砂岩2种岩样进行了三轴围压实验，提出泊松比函数的概念。根据常规岩石受力变形分段研究的方法，将泊松比函数分段表示，表征岩石的不同受力变形阶段，结合实验数据拟合出了泊松比函数的实际表达式。泊松比函数反映岩石在开始受载到破坏的整个过程中泊松比数值的变化规律，可利用其解释岩石在加载和破坏的过程中一些物理现象。

1 实验及概念定义

1.1 实验方案

采用三轴围压测试设备，对30 MPa下的南充砂岩和武胜砂岩2种岩样进行三轴压缩实验，并实时记载岩石的整个加载过程。实验装置主要记录加载过程中的轴向主应力、主应变及侧向主应变。岩石力学测试实验设备为美国GCTS公司RTR-1000型动三轴岩石力学测试系统。该系统最大轴向压力1 000 kN，最大围压140 MPa，孔隙压力140 MPa，温度150°C，实验控制各参数精度 （压力0.01 MPa，液体密度0.9 g/cm3，变形0.001 mm）。压力室内上下承压板硬度不低于HRC58，不平行度小于0.02 mm的测量精度，加载范围满足：

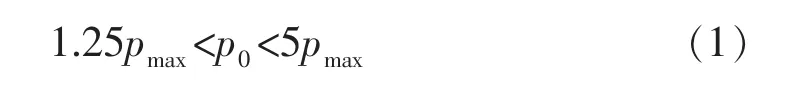
式中：p0为材料实验机度盘最大值，N；pmax为预计试件的最大破坏载荷，N。

实验所用岩样为圆柱体试件，其表观参数为直径50 mm±1 mm，高径比2.0±0.2。试样两端面不平行度不超过0.1 mm。将试件安装于岩石力学测试系统，逐步加载，采集与载荷、位移和应变测试器连接的计算机数据采集系统的实验数据。

1.2 实验结果

基于上述实验平台，利用计算机数据采集系统采集到的实验数据考察泊松比变化规律。提取出岩样从开始受载到破坏的整个过程中的径向应变ε2，ε3和轴向应变ε1，计算泊松比ν。本文选取了岩石受力变形各个阶段样品点30个，可以准确表示岩石的受力状态。南充砂岩和武胜砂岩在30 MPa围压下，各个变形阶段中部分典型特征点的轴向和径向应变见表1、表2。

表1 围压30 MPa下南充砂岩泊松比

表2 围压30 MPa下武胜砂岩泊松比

同时，借助于南充砂岩和武胜砂岩应力应变图，依照分段思想讨论岩石受力变形的各个阶段。根据应力应变图中各个阶段分界点的轴向应变，将泊松比曲线进行分段处理。将实验数据分别进行处理并绘图，可以得到围压30 MPa下南充砂岩和武胜砂岩泊松比变化（见图1）。

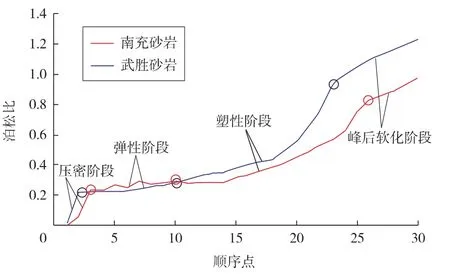
图1 围压30 MPa下砂岩泊松比变化

由图1可以看出，泊松比从压密阶段逐渐增大直到弹性阶段，但压密阶段相对来说持续时间较短。压密阶段泊松比迅速增大，在实际岩石力学分析中的意义不大。南充砂岩和武胜砂岩泊松比在加载全程的变化规律大致类似，但在各个阶段持续的时间不同，泊松比变化快慢不一样。南充砂岩和武胜砂岩弹性阶段的波动相差不大。南充砂岩的塑性变形阶段较武胜砂岩长，泊松比增长相对慢，但武胜砂岩峰后软化变形阶段比南充砂岩峰后软化阶段持续时间更长。

之所以南充砂岩和武胜砂岩在受力变形过程中泊松比不同，主要是2种岩石的致密性不同，各自组分存在差异，2种岩石形成机理不同。在进行三轴围压实验时，由于岩石内部结构的不同，岩石受力时的轴向变形和径向变形不一样，导致计算出来的泊松比不同。一般而言，不同岩石的泊松比不同。

1.3 结果分析

图2为常见三轴压缩实验应力应变示意图，4个变形阶段分别为压密、弹性、塑性和峰后软化阶段。

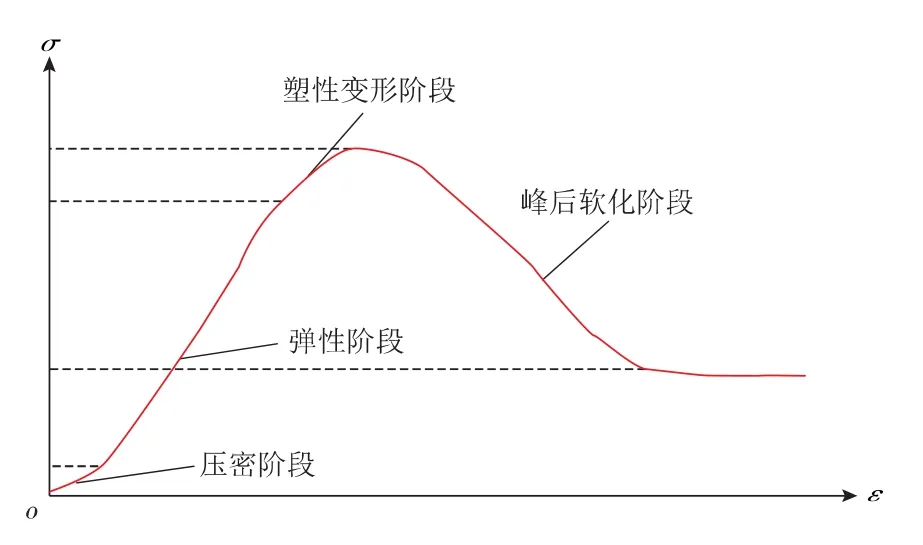
图2 典型三轴压缩实验应力应变示意

从表1得出，南充砂岩全程平均泊松为0.388，而弹性阶段（一般指比例阶段）的泊松比为0.233。因此，南充岩石在压密阶段泊松比很小，值得说明的是，压密阶段岩石内部孔隙迅速闭合，岩石变形较大，该阶段的泊松比不具有通用性；在弹性阶段，泊松比保持在0.230左右，基本趋于稳定，这就是标准的泊松比；在塑性阶段，泊松比上升较快，而且明显大于弹性阶段；在峰后阶段，泊松比会快速增大，直至0.973，此处需要说明的是，峰后阶段岩石试样已经处于高损伤、准破坏状态。可以看出，岩石在围压作用下泊松比是一个不断增大的值，这个规律和上文的讨论结果保持一致，这也充分说明用岩石弹性阶段的平均泊松比在力学应用中作为整个过程的变形参数是不太合理的。

从表2可以看出，武胜砂岩压密阶段持续时间很短，并且泊松比数值都是在0.200以下。围压30 MPa武胜砂岩的平均泊松比为0.387，而弹性阶段的平均泊松比约为0.217。塑性阶段是泊松比的增长期，但峰值前的增长还是相对比较慢；峰后软化阶段，泊松比会快速增大，增加至1.231。此处需要说明的是，根据实验材料和条件的不同，各类岩石的最大泊松比一般都不相同。

综上所述，岩石在压缩变形的整个过程中，泊松比的变化是很大的，但目前只见王学滨［12］对岩样单轴压缩峰值后泊松比理论进行过研究。

2 泊松比函数的提出

在三轴压缩实验条件下，岩石泊松比的变化规律可以从物理意义上解释。岩石试样在受压初期属压密阶段，此时岩石内部的孔隙和裂缝会产生闭合，侧向变形较小，泊松比几乎趋于0，且压密阶段相对其他阶段较短，对整体影响不大；继续加载，岩石会发生弹性变形，此阶段岩石内部几乎没有孔隙，这一阶段的变形和金属在弹性范围内的变形很相近，可以认为其泊松比是个定值，但岩石颗粒间的黏聚力相对比较小，所以泊松比也会略有增加；塑性变形阶段，岩石试样内部裂纹从萌生到增长，刚度减小，此时泊松比可以反映轴向和侧向应力及位移的关系；当继续加载时，岩石出现宏观裂纹，并且裂纹延伸至表面，其内部颗粒之间的摩擦和黏聚力就会变小，刚度急剧下降，导致其泊松比会急剧增大。

由图1可以看出，峰后软化阶段和塑性阶段曲线变化很陡峭，这也正好可以反映峰值处是岩石内部开始破坏的一个分割点。

以上分析表明，岩石的泊松比是个变化很大的数值，之前的学者将其作为定值研究是存在很大误差的。笔者依据上述分析认为，岩石的实际泊松比与范围变量、标准泊松比、峰值处的泊松比及最大泊松比存在着某种函数关系，其定义为

式中：ν*为实际泊松比，即三轴围压状态下岩石的泊松比；νs为标准泊松比，即平常测量的恒定泊松比；νp为峰值处的泊松比；νmax为三轴围压状态下最大的泊松比；x为大于0的变量。

研究图1曲线发现，岩石的泊松比变化规律可以进一步用函数来近似表示，以便更精确地应用于岩石力学中。函数表达式为

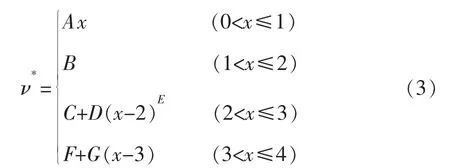
式中：A，B，C，D，E，F，G为一系列无量纲参数，用于拟合数据得到岩石泊松比具体表达式；0＜x≤1为压密阶段，1＜x≤2为弹性阶段，2＜x≤3为塑性阶段，3＜x≤4为峰后软化阶段。

3 泊松比函数的统一表达式

3.1 南充砂岩

由图1可以看出：在压密阶段，泊松比几乎是一个线性函数，而νs=0.233，因此，可以确定出式（3）中A= 0.233；在弹性阶段，泊松比近似为一个常数，所以B= 0.233；而在塑性阶段，泊松比函数呈几何非线性增长，因此，需要进行数据拟合求出C和D。

由表1实验数据可知，νp=0.829，νs=0.217。将南充砂岩塑性阶段的实验数据导入Matlab中，根据式（3）选择合适的函数，采用最小二乘法和幂函数应用法进行数据拟合。拟合出来的数值为C=0.343，D=0.492，E= 2.387。塑性阶段的泊松比函数表达式为

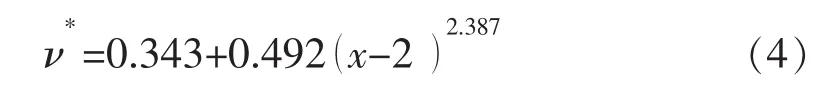
同理，将南充砂岩峰后软化阶段的实验数据导入Matlab中，选择线性函数拟合，拟合出来的数值F= 0.829，G=0.144。峰后软化阶段岩石的泊松比函数表达式为

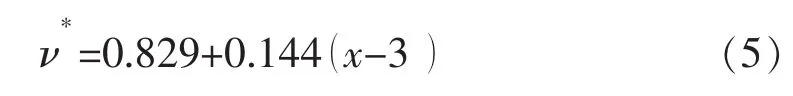
综上所述，南充砂岩的泊松比函数式为

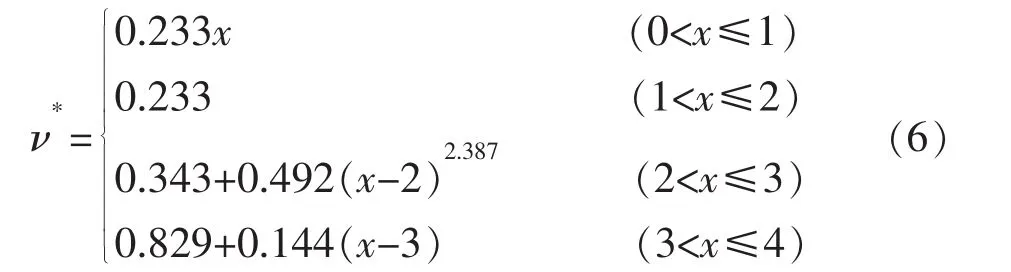
由于塑性阶段是重点研究对象，将塑性阶段拟合出来的泊松比函数曲线与实际泊松比函数对比，结果见图3。由图可见，拟合出来的曲线与实际曲线相近。

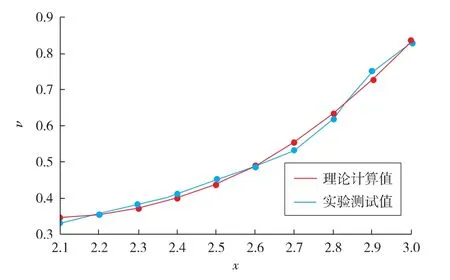
图3 南充砂岩塑性阶段泊松比实验值和理论值

3.2 武胜砂岩

同理，将表2中数据导入Matlab中，按照前文所述南充砂岩的数据处理方式，选择式（3）的函数形式来拟合数据，可以得到武胜砂岩的函数表达式为

拟合出塑性阶段的泊松比曲线，与实际塑性阶段泊松比曲线对比结果见图4。可以看出两者很相近，说明拟合出的函数有较好的实用性。

图4 武胜砂岩塑性阶段泊松比实验值和理论值

4 泊松比函数对岩石试样破坏的解释

砂岩泊松比函数的统一表达式（式（6）、式（7））已经求出了各个参数的具体数值，拟合出来的方程和实验测量出来的数值非常吻合，由此可以说明笔者提出来的泊松比函数是正确的。

从图1泊松比的变化可以推理出：在压密阶段，岩石试样只是孔隙闭合，并没有发生破坏，此阶段泊松比函数呈线性增长，反映了横向和纵向的变化逐渐增大，且呈现比例关系。从压密阶段到弹性阶段，A=B，可以看出其压缩过程的连续性。在弹性阶段，岩石内部孔隙为0，近似于金属的比例压缩阶段，泊松比波动变化不大，相对稳定。塑性阶段是本文研究泊松比函数的重点，在该阶段，岩石的应力应变曲线呈现非线性、幂函数趋势，岩石内部孔隙和裂纹萌生，损伤比较明显，E约为2.000（南充砂岩为2.387，武胜砂岩为1.746），说明塑性阶段泊松比函数呈二次函数增长趋势，即后一点总比前一点损伤严重。对于不同类型的岩石，E越大，表明破坏越快。在峰后软化阶段，泊松比函数呈现线性增长，并且数值都比较大，说明这一阶段岩石已经高度损伤或破坏。

据此可知，泊松比函数中的某些参数能说明岩石的性质，泊松比函数也能说明岩石破坏的规律。

5 结论

1）岩石的泊松比是随着载荷的增加而不断变化的，本文首次提出了泊松比函数的概念，并根据岩石受载变化特征用分段函数来表示泊松比函数。通过对实验过程和实验数据分析，确定了泊松比函数的具体表达式。

2）研究发现：岩石压密阶段的泊松比满足线性变化规律；弹性阶段的泊松比趋于一个常数，相当于标准泊松比；塑性阶段的泊松比呈幂函数变化规律；峰后软化阶段的泊松比呈现快速线性增长规律，直至岩石被破坏。

3）通过对泊松比函数表达式中的参数分析，发现泊松比函数能反映岩石在不同阶段的损伤和破坏规律。

4）建议对其他类型的岩石进行分析，寻求泊松比函数在岩石力学中普遍适用的规律，同时探讨多种围压条件下泊松比的变化规律。

［1］张年学，盛祝平，李晓，等.岩石泊松比与内摩擦角的关系研究［J］.岩石力学与工程学报，2011，30（1）：2599-2609.

［2］Poisson S D.Mémoires de l′académie des sciences de l′institut de france［M］.Paris：Nabu Press，2010：357-570.

［3］LAKES R S.Foam structures with a negative Poisson′s ratio［J］. Science，1987，235（4792）：1038-1040.

［4］EVAN K E，NKANSAH M A，HUTCHINSON I J，et al.Molecular network design［J］.Nature，1991（353）：124-125.

［5］曹文贵，方祖烈，唐学军.岩石损伤软化统计本构模型之研究［J］.岩石力学与工程学报，1998，17（6）：628-633.

［6］李晓.岩石峰后力学特性及其损伤软化模型的研究与应用［D］.徐州：中国矿业大学，1995.

［7］曹文贵，赵明华，刘成学.基于Weibull分布的岩石损伤软化模型及其修正方法研究［J］.岩石力学与工程学报，2004，23（19）：3226-3231.

［8］许江，李树春，刘延保.基于Drucker-Prager准则的岩石损伤本构模型［J］.西南交通大学学报，2007，42（3）：278-282.

［9］曹文贵，李翔.岩石损伤软化统计本构模型及参数确定方法的新探讨［J］.岩土力学，2008，11（29）：2952-2956.

［10］WANG Q，JI S.Poisson′s ratios of crystalline rocks as a function of hydrostatic confining pressure［J］.Journal of Geophysical Research Solid Earth，2009，114（B9）：175-192

［11］刘斌，席道瑛.不同围压下岩石中泊松比的各向异性［J］.地球物理学报，2002，45（6）：880-889.

［12］王学滨.岩样单轴压缩峰后泊松比理论研究［J］.工程力学，2006，23（4）：99-103.

［13］潘华，陈国兴，孙田.原状海洋土动泊松比的实验研究［J］.岩土力学，2011，32（1）：376-350.

［14］黄兴建，付小敏，沈忠，等.三轴循环荷载作用下岩石动态特性参数研究［J］.中国测试，2016，42（7）：117-122.

［15］SMITH C W，WOOTTON R J，EVANS K E.Interpretation of experimental data for poisson′s ratio of highly nonlinear materials［J］. Experimental Mechanics，1999，39（4）：356-362.

（编辑 王淑玉）

Proposition and research on rock′s Poisson′s ratio function

TIAN Jialin1，2,WU Bo1,WU Kaisong1,ZHAO Pan1
(1.School of Mechatronic Engineering,Southwest Petroleum University,Chengdu 610500,China;2.School of Mechanical Engineering,Southwest Jiaotong University,Chengdu 610031,China)

Poisson′s ratio,which reflects the deformation ratio of material′s transverse and longitudinal deformations under load conditions,is a very important material parameter of material properties,and it has a clear physical meaning.However,compared with metals,rock′s Poisson′s ratio is not a constant,and its change law is worthy of further studying.Based on the triaxial compression tests on Nanchong and Wusheng sandstones,this paper proposes the concept and formula of Poisson′s ratio function. The relationship between Poisson′s ratio function and standard Poisson′s ratio and the relationship between the Poisson′s ratio at the peak and the maximal Poisson′s ratio are obtained.Finally,the physical meanings of all material parameters in Poisson′s ratio function are analyzed.Poisson′s ratio function explains physical phenomena in the rock deformation process,which has some practical significance.

elastic constant;triaxial compression test;Poisson′s ratio function;standard Poisson′s ratio

国家自然科学基金项目“单次冲击加卸载后岩石的全程动态应力应变关系研究与应用”（51174173）

TE12；P634.1

：A

10.6056/dkyqt201701005

2016-07-03；改回日期：2016-11-26。

田家林，男，1979年生，副教授，博士，主要从事机械设计及理论、井下工具、钻井动力学及理论研究。E-mail：tianjialin001@gmail.com。

田家林，吴波，伍开松，等.砂岩泊松比函数的提出及研究［J］.断块油气田，2017，24（1）：21-25.

TIAN Jialin，WU Bo，WU Kaisong，et al.Proposition and research on rock′s Poisson′s ratio function［J］.Fault-Block Oil&Gas Field，2017，24（1）：21-25.