基于核密度估计的点群密度制图应用研究

卢 敏,杨 柳,王金茵,黄 煌,王结臣

(1.江苏省地理信息技术重点实验室，江苏 南京 210023;2.南京大学 地理信息科学系，江苏 南京 210023;3.江苏省基础地理信息中心，江苏 南京 210013)

基于核密度估计的点群密度制图应用研究

卢 敏1,2,杨 柳3,王金茵1,2,黄 煌1,2,王结臣1,2

(1.江苏省地理信息技术重点实验室，江苏 南京 210023;2.南京大学 地理信息科学系，江苏 南京 210023;3.江苏省基础地理信息中心，江苏 南京 210013)

随着信息技术的发展，点状专题数据激增，需要突破传统制图方法的表达局限，利用海量点群数据对专题信息进行快速、直观、综合的制图表达。文中以南京市银行的ATM网点数据以及全国KTV营业点分布为制图数据源，探讨了点群数据核密度估计图以及三维核密度曲面图的制作方法，并对其中的关键技术作了深入的研究。研究表明，基于核密度估计的网点密度制图方法，消除了边界分隔对密度计算精度的影响，能更好反映点群数据的空间分布密度、区域差异、动态变化等特征，具备更丰富的表现力。

核密度估计；点群密度制图；最佳带宽计算；三维核密度曲面图

点状分布是专题要素空间分布的最常见状态之一，比如银行、学校、超市、停车场、餐厅等[1]，这些点状分布的专题要素种类繁多、分布广泛，点群目标的制图表达适用范围广泛，通过合理运用丰富的专题地图直观、有效的可视化表达，可以综合多样地展现研究成果、直观地传达专题信息，并反映其空间分布的分布密度、区域差异、动态变化等特征，使读图者一目了然。从整体上看，点群要素最重要的特征是空间分布特征，如何直观、快速、有效地表达点群目标在空间中的数量、质量、密度和相互关系，是制图表达的重点[2]。随着信息技术的发展，数据获取能力的增强，许多领域、行业的点状专题数据激增，如何突破传统制图方法的表达局限，利用海量点群数据对专题信息进行快速、直观、综合的制图表达，成为了制图领域亟待解决的问题。

对点群要素空间分布特征的表达，应力求展现其分布密度的区域差异，进而揭示某些潜在规律，如居民行为习惯、事件发生热点、商圈吸引力等[3-4]。利用离散点要素进行制作密度图时，通常有两种思路。一种是将整个区域按指定的边界(如行政区)进行分割，统计各个区域内落入的点的数量，计算各区域的要素密度，从而将点要素转换为具有指定边界和不同值的面要素。在该思路中可采用量底法、点值法等方法制图，但是在这类依边界分隔的密度图中，制图表达的精度与区域划分的精细程度密切相关，区域划分越小，精度越高，区域划分越大，精度也就越低。因此，另一种思路是不进行区域分割，根据离散的点要素数据内插计算整个区域的值，从而生成一个连续的密度表面，通过颜色、符号等在底图上的叠加来展现专题要素的聚集特点[5]。根据内插原理的不同可分为简单点密度制图和核函数密度制图，可以采用等值线法、量底法、三角形图表法等方法制图。点密度制图与核密度制图均是通过将点状要素转换为连续曲面，并以面上某点的值代表该点的要素密度，来消除边界分隔对密度计算精度的影响，较好地展现了点群数据的聚集特点。

本次研究将以南京市所有银行的ATM(Automatic Teller Machine，自动柜员机)营业网点数据，以及中国大陆地区KTV(Karaoke Television，通常指提供卡拉OK影音设备与视唱空间的场所)营业网点数据为例，探讨核密度估计方法在密度制图中的应用。

1 核密度估计

1.1 核密度估计的基本原理

事件在空间上的出现具有一定的随意性，但这种随意性在一定的空间过程作用下会受到影响，从而导致其在不同位置上出现的概率或高或低。如果某一区域出现更多的事件，则可以认为事件在受到某种空间作用下在此处出现的概率会更高，反之则更低。结合地理学第一定律空间自相似的规律特征，这种密度(或者概率)上的变化可以用来区分事件在空间上的分布模式[6-8]。核密度估计(Kernel Density Estimation, KDE)方法就反映了这一思想，它认为区域内任意位置都有一个可测度的事件密度(也称强度)，该位置的事件密度可以通过其周围单位面积区域内的事件点数量来估计[9-10]。核密度估计可以想象成一个移动的三维函数(内核)，其影响范围内的事件点到s的距离视为事件点对s影响的权重值，进而计算出点s处的事件密度[11]。

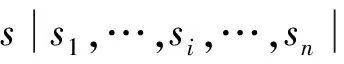
(1)

式中：k( )表示的是核的权重函数，τ>0，称作带宽，即以s为原点的曲面在空间上延展的宽度，τ值的选择会影响到分布密度估计的光滑程度；s-si是密度估值点s和si之间的距离。对于核密度估计的结果，可以采用合适的等值线算法或者以栅格的形式，将研究区域R以密度变化的连续表面来表示。

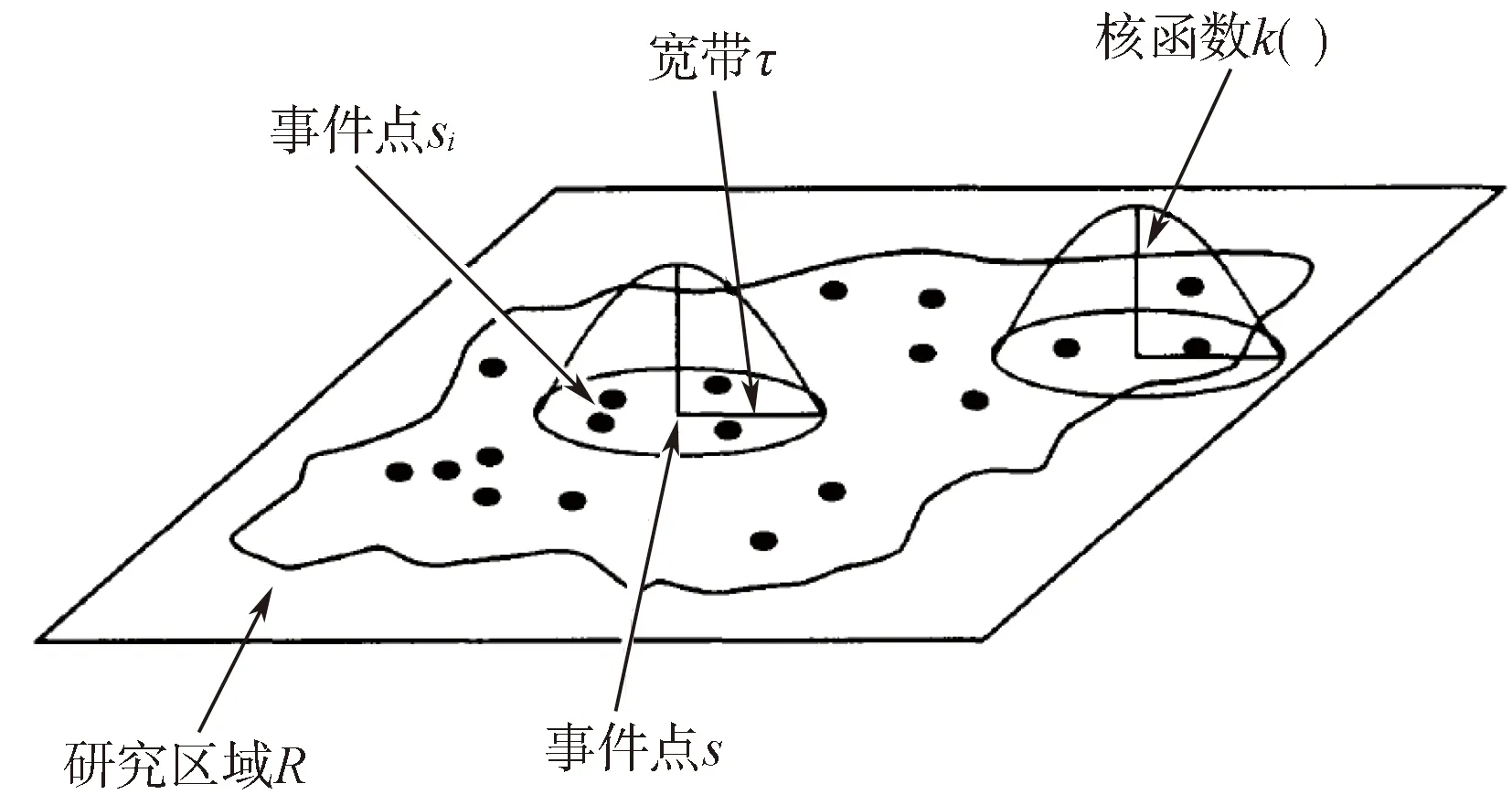
图1 对点模式的核密度估计

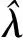
(2)

式中：τ为核函数的带宽，di为事件点到s的距离。研究表明，不同数学形式和核函数对密度估计的影响很小，对KDE的曲面特征影响较大是带宽τ的选取。因此,带宽的选择比较重要，而核函数可以根据实际需求选择即可。

1.2 最适带宽的计算方法

在KDE方法中，带宽的确定至关重要，在很大程度上会影响到分析的结果。实际的经验表明，如果想要更光滑的密度表面，τ的值可以设的大一些，然而此时就有可能掩盖想要探测的热点区域；而如果将τ的值设的太小，所得到的密度表面变化就会变得突兀不平，即局部的特征会得到凸显，而忽略了稍大尺度上的整体关联性，使得热点区域过于分散。因此，在KDE方法的实际应用中，需要采用合适的方法计算得到τ的取值，探索相应带宽值τ下密度表面的光滑程度，以检验该带宽下的KDE结果是否合理。

一些学者经过研究总结出一些最适值的计算方法，其中最简单的一种是根据事件点数据的最小外接矩形确定，即用最小外接矩形的较短边除以30来确定τ值，即

(3)

这种方法缺点是仅考虑了研究区的形状特征，而没要考虑事件点数量的影响。

一种改进的τ值确定方式是，首先确定整个事件点的平均中心，然后计算平均中心到各个事件点的距离，取这些距离的中位数Dm，并计算事件点的标准距离SD(所谓标准距离与标准差类似，是对事件点的一种概括性描述)，则τ值满足公式[12]

(4)

式中,n为事件点数量。

Bailey和Gatrell给出τ的建议值[13]，其采用事件点数量的0.68倍的-0.2次方与研究区面积的平方根的乘积确定，即

(5)

式中:n为事件点数量，A为研究区面积。

上述几种方法中均没有考虑事件点之间的空间关系，因此，有学者提出一种基于事件点之间的k阶最邻近距离方法来确定τ值[14-15]，即

(6)

其中,dij表示k阶最邻近距离，即从一个事件点一直到第k个最邻近点的距离均值。k值决定了密度表面的光滑程度，k值越大带宽τ也就越大，生成的密度表面也就越光滑。

2 核密度估计的密度制图

核密度制图的思路是，给每个点要素定义一个圆形邻域，在其上方覆盖一个平滑曲面，依据二次核函数运算使曲面值呈正态分布，在该点所在位置处曲面的值最高，随着与点的距离的增大曲面值逐渐减小，到邻域边界处减小为零。其中，曲面最高值所在点到圆形邻域值为零处的距离，就是带宽。每个输出像元的密度均为叠加在该栅格像元中心的所有密度曲面值之和。

平面视角下的核密度估计，涉及的主要参数为带宽。根据已有文献的研究成果[16-17]，总结出几种带宽的计算方法。但是由于这些带宽的计算方法对于数据集的侧重点各不相同，因此分别计算所得到的带宽值差异较大。在具体研究中，通常的做法是：首先利用这几种方法分别计算来得到可选的带宽，然后将其作为参数分别进行核函数估计，最后根据曲面的平滑程度，以及是否能兼顾全局趋势信息与局部热点信息，从而最终确立合适的核密度估计带宽。

本次研究以南京市主城区的ATM网点数据为例，研究区包括了南京市的主要城区范围(面积约为254.86 km2)，银行ATM数据来源于网络电子地图，研究中主要选择了南京市主城区范围内网点数量大于50的商业银行ATM网点，包括工商银行、建设银行、农业银行等合计749家ATM网点。其他主要参数和带宽的计算结果如表1所示。

表1 研究区带宽计算结果

根据表1的计算结果分别就4种不同的带宽进行密度估计计算，其结果如图2所示。由于不同带宽下计算所得到密度估计值的方法各不相同，为了更好地比较4种带宽密度估计的影响，在分级渲染的过程中并不能采用统一的分级断点，这里统一采用“自然断点”进行分级。

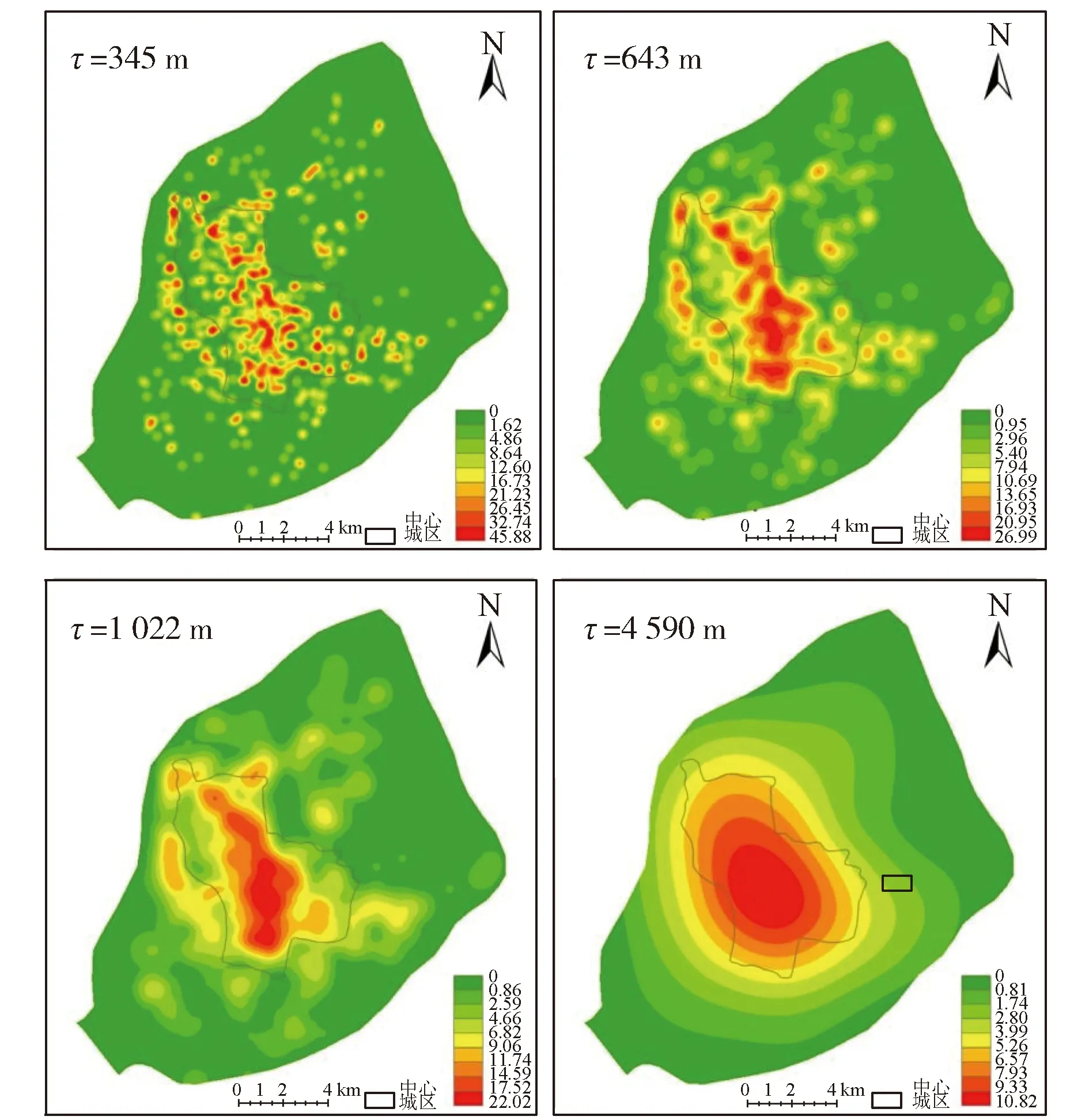
图2 不同带宽下的核密度估计结果

由图2可以看出，随着带宽的增大，密度估计表面越来越趋向于光滑，特别是当τ= 4 590 m时，整个密度曲面基本上呈现一种由中心向外围扩散的圈层结构，虽然这在一定程度上反应了ATM网点在南京主城区范围内分布的大体趋势(由中心城区向外围递减)，但对网点分布的热点区域探测并没有太大的用处。对于其他3种方法而言，采用τ=643 m和τ=1 022 m这两种带宽的效果均较为理想，在反映网点分布的整体趋势的同时，也能够很好地呈现局部的热点区域信息；k阶最邻近距离方法这里取k=3时计算所得的带宽，即τ=345 m，可以看出其探测出的热点区域最为分散，对网点分布热点区域的探测而言尺度过小。但是事实上，k阶最邻近距离方法具有很强的灵活性，上述其他几种方法计算得到的带宽都能在k阶最邻近距离方法相应的阶数下找到对应的值，因此，一种选择合适带宽的方式可以是：首先通过默认方法计算其带宽，然后在k阶最邻近距离方法中找到对应的阶数，并以此为基准，增加或减少阶数直到找到适合的带宽，得到较好的视觉效果。

KDE的方法消除了样方分析中由于样方的尺寸和形状等对局部密度的影响，并且具有更好的可视化效果，在探索事件分布热点、测度局部密度概括指标上具有一定的优势。然而KDE虽然能够对具有一阶密度或平稳性的分布模式做出有效且实用的检验，但对于二阶距离特性的探测还显得不够。

3 三维核密度曲面图

将普通二维专题地图进行三维显示，通过对专题信息的立体化表达，能给读图者带来更直接更具冲击力的视觉感受。同时，三维制图还有助于减弱专题地图中对色彩的依赖，使地图适应传统印刷工艺对色彩的限制。在立体的现实世界中，具有高低起伏特点的景观有很多，纵横交错的山脉、鳞次栉比的楼宇，都可以作为三维制图的效果参照。受人们阅读习惯和设备制作工艺的限制，目前常用的图形显示设备依然采用平面显示方式，三维效果通常需要依靠物体形状、颜色、阴影、辅助线等的辅助渲染来体现[18]。

相对于平面地图而言，三维模拟更形象、直观，也更符合人们日常观察事物的习惯。三维表面图的应用较为广泛，不仅可以直观地展现高程、气温、人口密度等连续变量，还可以通过叠加其它要素参数来表达综合专题信息。在点群要素三维制图表达中，可根据数据特点和地图用途的不同，选取适当的制图表达方法，结合构图和色彩搭配，可以形成较好的效果。较高的区域会遮挡后面较矮的区域，若要较好地掌握数据的整体状况，需从多个角度进行观察。对地形的三维模拟多从这两种视角出发，或是如身临其境般的虚拟现实场景，或是用沙盘等立体模型展现地势起伏。为了更好地展现制图区域内的总体情况，地形模拟更多地采用了俯瞰的视角。然而，从地图制图的角度来看，在现有的专题地图制图表达方法中，三维地图制图方法一般用于自然地理要素的表达，如地形的高低起伏、温度的变化、降雨量地区差异的展示等[19]，但对于人文地理要素中社会经济现象的空间分布特征而言，三维的制图表达手段更加直观、丰富多样，但却是少有人运用该方法来呈现此类人文地理要素的空间差异特征。刘锐、胡伟平等人[20]利用核密度估计模型与基尼系数为切入点，以我国沿海11个省份2000—2012年的数据为例，绘制了海洋经济发展的动态演变趋势与规律，但也依旧没有使用三维制图进行专题制图展示。

本次制图所用的KTV营业网点数据是通过网络电子地图整理得到的。作为一种典型的娱乐休闲行业，KTV行业在中国的发展并不均衡。经统计，在占大陆地区全部国土面积13.5%的东部地区12省(或自治区、直辖市)中，共有KTV营业网点44 637个，占大陆地区KTV网点总量的50.9%；在占大陆地区国土面积29.3%的中部地区9省(或自治区)中，拥有KTV营业网点24 883个，占大陆地区KTV网点总量的28.4%；西部地区的10个省(或自治区、直辖市)占据大陆地区国土面积的57.2%，共有KTV营业网点18 210个，仅占大陆地区KTV网点总量的20.7%。利用前文所描述的核密度最佳带宽确定方法，首先分别计算出4种方法对应的带宽，然后分别用这4个带宽作出核密度估计图，通过视觉的对比，选出其中能兼顾全局趋势信息与局部热点信息的密度图，从而确定制图的最佳带宽。通过该最佳带宽做出平面图后添加俯瞰视角的三维显示效果，可以得到如图3所示的效果图。

可以看到，将平面的核密度图拉伸成立体曲面后，密度较高的区域得到有效拉伸，辅以色彩上的区分，能够有效突出了区域间的差异。经过三维立体化并拉伸显示后的核密度曲面，高低值之间的差异被适当地夸大，这样可以有效地凸显出热点，如图3所示的上海、北京、广州等，均是KTV密度最高的几个城市。此外，在三维核密度曲面上叠加了注记、图例、行政边界等辅助读图的地图要素之外，由于三维透视中存在显示比例近大远小的变化，图中无法添加比例尺，为了弥补这一缺憾，在制图中还添加了规则的格网，它不仅使读图者对空间位置的把握更准确，并且有指示方向的作用。因此在制图的过程中，应当根据制图数据的特点和制图需要选取合适的角度，全面、清晰、直观地展现空间和属性信息，提升地图的可读性和可用性。

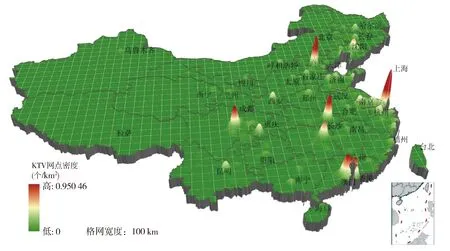
图3 中国大陆KTV营业网点三维密度图

4 结束语

大多数专题制图要素在空间上的分布是不均衡的，使用传统的专题地图制图表达手法往往受区域几何面积、分区单元大小等的影响，不能直观地展现局部统计信息的密度差异。在诸如量底法这类依边界分隔的密度图中，制图表达的精度与区域划分的精细程度相关，区域划分越小，精度越高，就越能消除分区间的密度差异，分区间的密度分布越平滑；反之区域划分越大，精度也就越低，分区间的密度差异越大，密度分布越粗糙。

本文将核密度估计的相关理论运用到空间点群数据的制图上，分析了不同数据源的情况下KDE函数带宽的变化对核密度制图的影响。研究表明，利用核密度估计的方法能够计算得到较为平滑的密度分布，能有效消除边界分隔对密度计算造成的影响。而三维曲面图用立体模型展现其凸起和凹陷，从而使专题信息的展示更加直观多样。不仅有效地反映了专题要素的空间形态、数量特征，而且具有方向性和对比性，表现力出色。这两种方法是专题制图方法的扩充与发展，为点群数据的制图表达提供了一种新的思路。

[1] 周爱华,张宝秀,董恒年,等. 基于GIS的北京城区老字号小吃店空间分布特征研究[J].北京联合大学学报(自然科学版),2015,29(4):29-35.

[2] 曹一冰,付洪贝,潘志超. 地图设计中的美学研究[J]. 测绘与空间地理信息,2011,34(1): 231-233.

[3] 王劲峰. 地图的定性和定量分析[J]. 地球信息科学学报,2009,11(2): 169-175.

[4] 禹文豪,艾廷华. 核密度估计法支持下的网络空间POI点可视化与分析[J]. 测绘学报,2015,44(1):82-90.

[5] 祝国瑞,郭礼珍,尹贡白,等. 地图设计与编绘[M]. 武汉：武汉大学出版社,2001.

[6] ANDERSON T K. Kernel density estimation and K-means clustering to profile road accident hotspots[J]. Accident Analysis & Prevention,2009,41(3): 359-364.

[7] 闫庆武,卞正富,赵华. 人口密度空间化的一种方法[J]. 地理与地理信息科学,2005，21(5): 45-48.

[8] 张桂铭,朱阿兴,杨胜天,等. 基于核密度估计的动物生境适宜度制图方法[J].生态学报,2013,33(23):7590-7600.

[9] XIE Z,YAN J. Kernel Density Estimation of traffic accidents in a network space[J]. Computers,Environment and Urban Systems. 2008,32(5): 396-406.

[10] XIE Z,YAN J. Detecting traffic accident clusters with network kernel density estimation and local spatial statistics: an integrated approach[J]. Journal of Transport Geography. 2013,31(0): 64-71.

[11] OKABE A,SATOH T,SUGIHARA K. A kernel density estimation method for networks,its computational method and a GIS-based tool[J]. International Journal of Geographical Information Science. 2009,23(1): 7-32.

[12] ArcGIS10.2在线帮助文档中核密度估计函数的默认带宽设定[EB/OL]. http://resources.arcgis.com/en/help/main/10.2/index.html#/How_Kernel_Density _works/009z00000011000000/ . (2014,10).

[13] BAILEY T C,GATRELL A C. Interactive spatial data analysis[M]. Longman Scientific & Technical Essex,1995.

[14] 王远飞,何洪林. 空间数据分析方法[M]. 北京：科学出版社,2007.

[15] WILLIAMSON D,MCLAFFERTY S,GOLDSMITH V,et al. A better method to smooth crime incident data[J]. ESRI ArcUser Magazine. 1999: 1-5.

[16] SCOTT D W. Multivariate density estimation: theory,practice,and visualization[M]. John Wiley & Sons,2015.

[17] SIMONOFF J S. Smoothing methods in statistics[M]. Springer Science & Business Media,2012.

[18] 徐智勇,艾廷华,危拥军，等. 三维地图符号视觉参量研究[J]. 武汉大学学报(信息科学版),2006，31(6): 557-560.

[19] 叶思源,吴树仁,欧阳永龙. 地质三维可视化建模与其剖面自动制图应用研究[J]. 地质与勘探,2011,47(3):498-504.

[20] 刘锐,胡伟平,王红亮,等. 基于核密度估计的广佛都市区路网演变分析[J]. 地理科学,2011,31(1):81-86.

[责任编辑：刘文霞]

Applications of pointgroup density cartography based on kernel density estimation

LU Min1,2, YANG Liu3, WANG Jinyin1,2, HUANG Huang1,2, WANG Jiechen1,2

(1. Jiangsu Province Key Laboratory of Geographic Information Science and Technology, Nanjing University, Nanjing 210023, China;2. Dept.of Geographic Information Science, Nanjing University, Nanjing 210023,China;3. Jiangsu Province Surveying & Mapping Engineering Institute, Nanjing 210013,China)

With the development of information technology and the increase of thematic point data, it is necessary to break through the limitation of the traditional cartography and apply mass point group data to express thematic information more quickly, intuitively and comprehensively. This paper, taking ATM network data of banks in Nanjing and KTV network data in the whole country as given data, studies the methods to make kernel density map and 3D kernel density surface map and presents the key technology further. The study shows that the point density cartography based on the kernel density eliminates the influence of edge on the accuracy of calculating density and reflects the density of point distribution, the regional difference, dynamic change and other characteristics, so which has more abundant expression.

kernel density estimation; point group density cartography; optimal bandwidth computation; 3-D kernel density surface map

引用著录：卢 敏,杨 柳,王金茵，等.基于核密度估计的点群密度制图应用研究[J].测绘工程，2017，26(4)：70-74，80.

10.19349/j.cnki.issn1006-7949.2017.04.013

2016-02-25；

2016-03-19

国家自然科学基金资助项目(41571377)；国家自然科学基金资助项目(41401450)

卢 敏(1991-)，男，硕士研究生.

P283

A

1006-7949(2017)04-0070-05