复杂混响背景下声呐基阵的目标方位估计算法
2017-02-09张国光
张国光
(昆明船舶设备研究试验中心 昆明 650051)
复杂混响背景下声呐基阵的目标方位估计算法
张国光
(昆明船舶设备研究试验中心 昆明 650051)
在复杂混响背景下目标方位估计精度受到干扰限制较大,提出一种基于声呐基阵多源信息跟踪融合的复杂混响背景下目标方位估计算法。首先建立声呐基阵的多传感器分布式阵列信号处理模型,对声呐传感器阵列的传输信道模型进行空间重构和向量量化分解,建立Kalman滤波器进行混响抗干扰滤波,然后采用多源信息跟踪融合方法进行声呐基阵的目标方位和速度等信息的联合估计。最后进行仿真测试,结果表明,采用该方法进行复杂混响背景下声呐基阵的目标方位估计的精度较高,对水下目标的量化跟踪性能较好,实现了对目标的准确定位和检测。
混响; 声呐基阵; 目标方位估计; Kalman滤波; 信息融合
Class Number TN911
1 引言
随着水中兵器智能对抗技术的发展,水下目标对抗与反对抗的研究受到人们的极大重视,通过对水下目标的智能探测和方位估计,实现对目标的精确打击和跟踪识别。研究水下目标方位估计方法,将在研究智能水中兵器中具有重要的应用价值,相关的目标方位估计算法研究受到人们的关注。
采用声呐基阵进行水下目标的辐射信号的检测是实现目标量化跟踪识别的可靠性技术,声呐基阵堪称水下的耳朵,它是通过多个水声换能器组成的传感器阵列,通过传感器信号采集和处理方法,实现对监测区域的目标信息识别和估计。当目标的信源靠近阵列Fresnel区域时,声呐基阵将会发出探测脉冲进行目标信息的捕获,将采集声呐基阵信息输送到信号处理单元,在DSP芯片的处理下实现对目标检测信号的信息处理和识别,实现目标方位估计、速度估计以及其它信息特征的提取。由于水下环境恶劣,受到的海水混响等干扰因素较大,水下声呐基阵在进行目标检测和参量估计中的精度受到限制。针对上述问题,本文提出一种基于声呐基阵多源信息跟踪融合的复杂混响背景下目标方位估计算法。首先建立声呐基阵的多传感器分布式阵列信号处理模型,对声呐传感器阵列的传输信道模型进行空间重构和向量量化分解,建立Kalman滤波器进行混响抗干扰滤波,然后采用多源信息跟踪融合方法进行声呐基阵的目标方位和速度等信息的联合估计。最后进行仿真测试,得出有效性结论,展示了本文方法在提高声呐基阵对目标方位准确估计中的优越性能。
2 声呐基阵多传感器分布式阵列信号处理模型
2.1 声呐基阵多传感器阵列模型
研究声呐基阵多源目标方位估计的第一步是构建基阵传感器分布阵列发射模型,通过信号模型构建为建立波束形成图,并完成方位、速度等参量的估计,声呐基阵多传感器为近场源分布,假设为一个均匀线列阵模型,如图1所示。
声呐基阵作为阵元分布在均匀矩形网格中,阵列的边界是矩形,目标相对于阵列中心的距离可近似为
r≤2D2/λ
(1)
其中,D表示声呐传感器基阵的最大孔径,λ=c/f表示水下目标回波脉冲信号发射的中心频率f对应的工作波长。
假定由N=2P个阵元组成的间距为d均匀线阵表示声呐水声传感器基阵,在分布式阵列结构模型中,阵元间距dx,y轴方向的阵元间距为dy,满足:
(2)
设声呐传感器基阵阵列中心处的阵元坐标为0,以远场分布源为相位参考点,则第m个阵元的多源目标观测信号模型为

(3)
其中,si(t)为第i个阵列的波束形成复包络,xm(t)为传感器基阵阵元m接收的水下目标的回波脉冲信号,nm(t)为阵元m上的干扰噪声,φmi为阵元m相对于参考的传感器声呐基阵的相位差。
由Fresnel近似主动目标信号的频率时延表达式为
≈γim+φim2
(4)

(5)
其中,d与λi满足d≤λi/4。声呐基阵多传感器阵列的分布函数p(ek|vk)的方差和均值服从分布如下:
-∞≤t≤+∞
(6)
通过上述处理,实现了声呐基阵多传感器阵列模型构建,进而进行目标方位估计。
2.2 声呐传感器阵列的传输信道模型
对声呐传感器阵列的传输信道模型进行空间重构和向量量化分解,对声呐基阵传感器信道模型作如下假设:

2) 声呐传感器基阵的阵元噪声nm(t)为零均值、白或色的高斯过程,可用多个点目标来模拟一个分布式目标;

4) 阵元间距d≤λi/4,而且N>L。
根据上述假设进行信道模型构建,得到复杂混响背景下声呐基阵定位的目标轨迹特征:
M(k)=H(k)x(k)+V(k)
(7)

E[V(k)VT(k)]

(8)
采用多传感器量化融合方法进行复杂混响背景下声呐基阵的传输信道拟合,得到过程噪声和声呐传输信号的特征w(k)与V(k)的关联维矩阵描述为
E[w(k)VT(k)]

(9)
其中RV(k)是一正定的实对称阵,在多传感器融合下,复杂混响背景下声呐基阵的目标方位估计问题转化为量化信息融合问题,采用协方差矩阵的特征分解方法,用点目标来模拟分布源以及基于一阶近似的分布源模型,此时分布源矩阵RV(k)唯一地分解成:
RV(k)=L(k)R(k)LT(k)
(10)


(11)
其中

(12)
通过单观测数据矢量融合,得到第m个阵元接收到的参量信息矩阵为

(13)
(14)
在上述构建的声呐传感器阵列的传输信道模型中,进行信号处理和目标方位估计。
3 混响抗干扰滤波及参量估计实现
3.1 问题的提出及混响抗干扰滤波处理
在上述进行了声呐基阵多传感器分布式阵列信号处理模型和信道传输模型构建的基础上,进行复杂混响背景下目标方位估计改进设计,为了克服当前方法进行目标方位估计的精度较差,受到干扰限制较大的弊端,本文进行方位估计方法的改进设计,提出一种基于声呐基阵多源信息跟踪融合的复杂混响背景下目标方位估计算法,建立Kalman滤波器进行混响抗干扰滤波,Kalman滤波函数为

(15)

(16)
计算2q阶矩阵Q*QH,得到复杂混响背景下声呐基阵回波的滤波协方差矩阵为
Y(k|k-1)=P-1(k|k-1)

(17)
其中:
F(k-1) =λ-1(k)[Φ-1(k-1)]T
P-1(k-1|k-1)Φ-1(k-1)
=λ-1(k)[Φ-1(k-1)]T
Y(k-1|k-1)Φ-1(k-1)
(18)
回波脉冲信号的二阶矩分别为

(19)

3.2 目标方位估计实现

={I-F(k-1)[F(k-1)+Q-1(k-1)]-1}
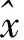
={I-F(k-1)[F(k-1)+Q-1(k-1)]-1}λ-1(k)


=λ-1(k){I-F(k-1)[F(k-1)+Q-1(k-1)]-1}

(20)
其中:

(21)


+R-1(k)-R-1(k)}
(22)
基于点目标假设的方位估计算法,结合多传感信息融合跟踪,得到声呐基阵t时刻阵列的接收数据矩阵为


(23)


(24)
令

(25)


(26)
接收阵列数据可以表示为

(27)

×F(k-1)
(28)

(29)
(30)

(31)
在全局最优解向量寻优下,得到目标方位和速度的联合估计运动参量输出为
(32)
根据目标的初始距离和速度,计算出第i个分布源的角信号分布函数,由此提高访问估计的精度。
4 仿真实验与结果分析
为了验证本文算法在实现复杂混响背景下声呐基阵的目标方位估计中的应用性能,进行仿真实验法分析,声呐基阵均匀线列阵阵元数N取值为20,水下运动目标方位是5°,两个信源的方位角分别为10°,30°,阵元间距假设为1/2倍波长,假设水下运动目标为点目标时,复杂混响背景下水下干扰的信噪比定为10dB,波速为1500m/s,声呐基阵阵元间距为最小波长的0.13倍,快拍数从200变化到2000,实验次数为200次,其它参数设定为θ1=-5o,Δ1=4o;θ2=3o,Δ2=5o;采用均方根误差作为目标方位估计的评价指标:
(33)

根据上述仿真环境和参数设定,得到声呐基阵对运动目标的谱峰搜索结果如图2所示。
根据图2所示的谱峰搜索结果,在角度方向上进行等高线投影,确定方位估计的等高线,得到目标方位估计的等高线扫描结果如图3所示。
从图可见,采用本文方法进行目标方位估计,能准确定位水下运动目标的位置,方位估计的精度较高,为了定量对比性能,采用本文方法,以方位估计的均方根误差为对比指标,得到结果如图4所示。从图可见,采用本文方法进行目标方位估计,误差能快速收敛到零,在复杂混响背景对水下运动目标方位估计性能较好。
5 结语
为了实现对复杂混响背景下的声呐基阵下运动目标的准确方位估计,本文提出一种基于声呐基阵多源信息跟踪融合的复杂混响背景下目标方位估计算法。首先建立声呐基阵的多传感器分布式阵列信号处理模型,对声呐传感器阵列的传输信道模型进行空间重构和向量量化分解,建立Kalman滤波器进行混响抗干扰滤波,然后采用多源信息跟踪融合方法进行声呐基阵的目标方位和速度等信息的联合估计。仿真测试结果表明,采用该方法进行复杂混响背景下声呐基阵的目标方位估计的精度较高,对水下目标的量化跟踪性能较好,实现了对目标的准确定位和检测,在水下制导武器设计中具有较好的应用价值。
[1] 郑振,王丽媛,周勇.混沌理论研究及其在舰船目标识别中的应用[J].舰船电子工程,2013,33(5):48-50.
[2] 周勇,甘新年,胡光波,等.鱼雷制导控制系统多通道控制加权算法设计[J].现代电子技术,2014,37(19):14-17.
[3] 葛立志.基于全弹道控制分析的水下航行器攻击模型视景仿真[J].舰船电子工程,2015,35(3):137-141.
[4] 胡光波,梁红,徐骞.舰船辐射噪声混沌特征提取方法研究[J].计算机仿真,2011,28(2):22-24.
[5] 李春龙,刘莹.一种高斯色噪声混响背景的宽带信号检测算法[J].科学技术与工程,2011,11(3):480-483.
[6] 秦宁宁,余颖华,吴德恩.移动混合传感网中节点自主部署算法[J].电子与信息学报,2016,38(7):1838-1842.
[7] MAHBOUBI H, MOEZZI K, AGHDAM A G, et al. Distributed deployment algorithms for improved coverage in a network of wireless mobile sensors[J]. IEEE Transactions on Industrial Informatics,2014,10(1):163-174.
[8] MAHBOUBI H. Distributed deployment algorithms for efficient coverage in a network of mobile sensors with nonidentical sensing Capabilities[J]. IEEE Transactions on Vehicular Technology,2014,63(8):3998-4016.
[9] 王洁,卢建朱,曾小飞.可及时确定受攻击节点的无线传感器网络数据聚合方案[J].计算机应用,2016,36(9):2432-2437.
[10] 罗泽峰,单广超.基于网络和虚拟多媒体技术的海战平台视景仿真实现[J].物联网技术,2015,5(3):91-92,94.
[11] BOUDIA O R M, SENOUCI S M, FEHAM M. A novel secure aggregation scheme for wireless sensor networks using stateful public key cryptography[J]. Ad Hoc Networks,2015,32(C):98-113.
DOA Estimation Algorithm of Sonar Array in Complex Reverberation Background
ZHANG Guoguang
(Kunming Shipborne Equipment Research and Test Center, Kunming 650051)
In complex reverberation background, DOA estimation precision is restricted by interference, this paper proposes an estimation algorithm based on multi-source information fusion tracking array complex reverberation sonar target azimuth. Firstly, the sonar array distributed multiple sensor array signal processing model, transmission channel model of sonar sensor array decomposition space reconstruction and vector quantization, reverberation anti interference filter Kalman filter is built, and then the joint estimation of multi-source information fusion tracking method for sonar array target range and speed information. Finally, simulation test is taken, simulation results show that it has high precision test, using the method of DOA estimation sonar array in complex reverberation background, it can quantify the tracking performance of the underwater targets, and realize accurate positioning and target detection.
reverberation, sonar array, DOA estimation, Kalman filter, information fusion
2016年7月10日,
2016年8月26日
张国光,男,硕士,助理工程师,研究方向:水下信号处理。
TN911
10.3969/j.issn.1672-9730.2017.01.006
