常压塔顶冷凝系统水露点预测

欧阳文彬， 胡海军， 武 玮， 李欣昀， 张耀亨， 程光旭

(1.西安交通大学 化学工程与技术学院， 陕西 西安 710049； 2.中国石油 兰州石化公司研究院， 甘肃 兰州 730060)



常压塔顶冷凝系统水露点预测

欧阳文彬1， 胡海军1， 武 玮1， 李欣昀2， 张耀亨2， 程光旭1

(1.西安交通大学 化学工程与技术学院， 陕西 西安 710049； 2.中国石油 兰州石化公司研究院， 甘肃 兰州 730060)

以常压塔塔顶石脑油的相对密度和蒸馏数据为基础，通过化工流程模拟软件Aspen Plus生成了一系列虚拟组分，计算了每个虚拟组分的摩尔分数、标准沸点、相对密度和相对分子质量，并估算了每个虚拟组分的临界性质和偏心因子。使用Peng-Robinson方程对常压塔塔顶油气馏分进行严格三相平衡计算，研究了烃-水之间的二元交互作用参数对水在烃相的溶解度及水露点的影响。假设塔顶油气体系形成的水相为游离水，研究了水在烃相的溶解度对水露点的影响。计算结果表明，烃-水之间的二元交互作用参数对水在烃相的溶解度影响非常显著，当交互作用参数取0.43时，计算的水的溶解度与API Data Book计算值一致。使用2种方法计算时，水在烃相的溶解度对水露点的影响均不明显。使用严格的三相平衡计算的水露点为384.65 K，比基于游离水假设计算的水露点高1.3 K。

常压塔顶冷凝系统； 塔顶油气； 水露点； 虚拟组分； Peng-Robinson(PR)方程

在石油炼制过程中，原油经过常压塔蒸馏后分成塔底油、侧线油和塔顶油气，塔顶油气进入塔顶冷凝系统进行冷凝冷却。塔顶油气的主要成分是石脑油和水蒸气，还有微量的HCl、H2S以及其他杂质气体。当塔顶油气的温度降至水露点温度以下时，一部分水蒸气冷凝下来，形成水相，HCl和H2S随之溶解于水相中， HCl-H2S水溶液可造成腐蚀和环境污染；当温度降至刚好使塔顶油气形成初始水相，即水露点时，水的pH值最低，甚至低于1[1-3]，将造成设备或管线的严重腐蚀。为了预测和控制水露点腐蚀，需要准确预测水露点温度。在原油的炼制过程中，原油中溶解的水和塔底汽提蒸汽均集中到塔顶油气中，加上塔顶冷凝系统大量的注水，导致塔顶油气中的水含量很大。因此，研究塔顶油气的相行为时将塔顶油气视为烃-水体系。

对塔顶油气进行相平衡计算时必须解决两个问题。第一，如何表征石脑油；第二，如何处理烃-水之间的相互作用。石脑油的表征方法分为真组分法[4-5]和虚拟组分法[6-7]两类。采用真组分法时需要石脑油的详细组分数据，但是石脑油成分非常复杂，不易获得其详细组分数据；虚拟组分法可以利用比重、蒸馏曲线、平均相对分子质量、轻端组分等比较容易测得的数据来表征石脑油，已被广泛应用于石油馏分的相平衡计算[8]。对于涉及烃-水-气三相平衡的烃-水体系，处理方法分为两类[9]，一是使用简化烃-水分层计算法，忽略烃在水相中的溶解性，认为水相是纯液体水(即游离水)；二是采用严格三相平衡计算法。事实上，因为烃在水相中的溶解度非常低[10-11]，游离水假设带来的误差很小，现在的商业化工流程模拟软件都将游离水假设作为缺省的方法[9]。但是，水在烃相中的溶解度比烃在水相中的溶解度高数个数量级[10-11]，对于笔者研究的塔顶油气体系，根据API Data Book[12]程序9A1.3计算的373.15 K时，水在烃相的摩尔分数达0.01。此时忽略水在烃相中的溶解度是否会对水露点的预测结果产生明显影响，尚无文献报道。对于烃-水体系，通常引入烃-水之间的二元交互作用参数来计算烃与水的相互作用[13-18]。使用状态方程来预测烃-水体系的相行为一直是这一领域研究的热点[15-18]。其中，基于Redlich-Kwong方程的状态方程，如Redlich-Kwong-Soave(RKS)方程[19]、Peng-Robinson(PR)方程[15,20]，因其计算过程简单并且结果精度较高而受到研究者的青睐。笔者运用化工流程模拟软件Aspen Plus V7.2，将塔顶油气中的石脑油处理成一系列虚拟组分，选用PR方程对塔顶油气进行严格的烃-水-气三相平衡计算及带有游离水的相平衡计算，并考察了水在烃相的溶解度对水露点的影响。

1 烃-水体系相平衡

气-液平衡时，各相温度和压力相等，而且各组分在各相的逸度相等。对于n元组分体系处于m相平衡时应该满足式(1)的条件。

T1=T2=…=Tm

p1=p2=…=pm

(1)

(2)

(3)

对混合物，式(3)采用如式(4)所示的混合法则[15,20]。用压缩因子表示的形式如式(5)所示。

(4)

Z3-(1-B)Z2+(A-3B2-2B)Z-

(AB-B2-B3)=0

(5)

式(4)中，kij为二元交互作用参数，其值一般需通过二元相平衡实验数据确定。

通过式(5)来计算逸度系数时，计算公式[15,20]如式(6)所示。

(6)

2 常压塔顶气的水露点温度预测

露点是指一个由多种组分组成的气态混合物，当温度降低到刚好使混合气体开始凝结第1滴液滴时的温度。对于烃-水体系，可能会出现富烃相和富水相2个液相，将出现初始烃相时的温度称为烃露点，将出现初始水相时的温度称为水露点。在常压塔顶的条件下，一般第1液相是富烃相，第2液相是富水相。

塔顶冷凝系统的进料物流为塔顶油气，出料物流包括污水、石脑油和瓦斯气。流程模拟时使用“反推”的方法，即将出料物流混合加热至塔顶条件来模拟塔顶油气。计算过程需要的数据包括塔顶压力、石脑油流量、水蒸气流量、瓦斯流量、石脑油的相对密度和蒸馏曲线。某炼油厂常压塔顶系统操作参数和石脑油蒸馏数据列于表1和表2。

表1 某炼油厂常压塔顶系统操作参数和物流性质Table 1 Operating parameters and stream properties of crude distillation unit overhead system in a refinery

表2 石脑油的蒸馏数据(ASTM D86)Table 2 ASTM D86 distillation data for Naphtha

2.1 虚拟组分处理

采用PR方程计算时需要知道每个纯组分的临界性质和偏心因子。但是塔顶油气成分非常复杂，很难得到其详细的化学组成。因此，采用虚拟组分法将塔顶油气中的石脑油处理成一系列虚拟组分。石油馏分的虚拟组分处理就是利用可以测得的数据，如密度和恩氏蒸馏或实沸点蒸馏数据，将石油馏分切割成有限数目的窄馏分，每1个窄馏分都视为1个纯组分，称为虚拟组分，以窄馏分的平均沸点、密度和平均相对分子质量表征该虚拟组分的性质；然后选择适合石油馏分的关联式计算每个虚拟组分的热力学性质，从而将复杂的石油体系转换为一个由多个虚拟组分构成的混合体系。处理过程如图1所示[8]。

选用Aspen Plus中的API-Mesh方法，计算得到每个虚拟组分的标准沸点(NBP)、相对密度(SG)、相对分子质量(MW)和摩尔分数，并估算了每个虚拟组分的临界温度(Tc)、临界压力(pc)和偏心因子(ω)，结果列于表3。

图1 石油馏分的虚拟组分处理框图[8]Fig.1 Flow diagram of pseudo-components processing for crude fraction[8]

2.2 水露点温度预测

使用PR方程计算各组分的逸度系数时，需要设置各组分之间的二元交互作用参数kij。由于烃组分之间的相互作用较小，计算时不考虑烃-烃之间的二元交互作用参数kij[15,20]。

表3 石油馏分虚拟组分的性质Table 3 Properties of pseudo-components for petroleum fraction

2.2.1 严格的三相平衡计算

采用严格的三相平衡计算时，通过设置烃-水之间的二元交互作用参数kij来表征烃-水之间的相互作用。在Aspen Plus中建立模型，并选用PR物性方法进行三相闪蒸计算，计算过程如图2所示。表4 列出了烃-水之间的二元交互作用参数kij取不同值时，塔顶油气体系的水露点温度、烃相流量、烃相中的水含量和水在烃相的溶解度。从表4可见，随着kij的增大，水在烃相的溶解度逐渐减小；当烃-水之间的二元交互作用参数kij取0时，烃相中水的流量为136.785 kmol/h，对应的水在烃相的摩尔分数为0.122；当烃-水之间的二元交互作用参数kij取1时，烃相中水的流量为0.657kmol/h，对应的水在烃相的摩尔分数为0.001。尽管烃-水之间的二元交互作用参数kij对水在烃相中的溶解度影响显著，但是对水露点温度的影响却不明显。

图2 严格三相平衡计算水露点的流程Fig.2 Calculation procedure of water dew point with rigorous three phase equilibrium表4 二元交互作用参数kij取不同值时的计算结果Table 4 The results derived from different binary interaction parameters kij

kijWaterdewpoint/KHydrocarbonphaseflowrate/(kmol·h-1)Waterphaseflowrate/(kmol·h-1)Solubilityofwaterinthehydrocarbonphase1)0384.471117.0136.7850.1220.1384.51994.073.3470.0740.2384.54929.941.1570.0440.3384.58895.023.7470.0270.4384.63875.513.9380.0160.5384.69864.68.2770.0100.6384.75859.14.9520.0060.7384.82855.92.9760.0030.8384.88855.31.7950.0020.9384.95855.61.0860.0011.0385.01856.40.6570.001

1) Mole fraction

根据API Data Book中程序9A1.3[12]计算得到384.65 K时水在石脑油中的溶解度为0.014(摩尔分数)。由图3可知，当二元交互作用参数设为0.43时计算的水在烃相中的溶解度与API Data Book计算值一致。所以，对于塔顶油气体系，烃-水之间的二元交互作用参数kij合理的取值为0.43。

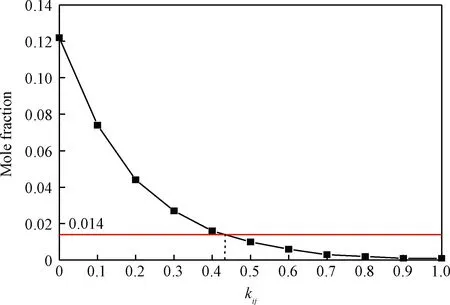
图3 二元交互作用参数对水在烃中的溶解度的影响Fig.3 The effects of interaction parameters on the solubility of water in hydrocarbon phase

2.2.2 简化烃-水分层计算法

简化烃-水分层计算法假设水相是纯液体水(即游离水)，而水在烃相的溶解度则由热力学方法或溶解度关联式，即API关联式9A1.3[12]来计算。假设水蒸气和气态烃的混合气体为理想气体，水和烃的分压用道尔顿分压定律计算。水的饱和蒸气压通过Aspen的STEAM-TA方法计算。基于以上假设知，随着温度降低，一部分烃逐渐冷凝下来，进而导致水的分压升高，当水的分压等于该温度下水的饱和蒸气压时，水蒸气开始冷凝形成水相，计算过程如图4所示。图4中的Aspen模型的物流组分为烃混合物，不包括水，所以压力p的初始值设置为塔顶条件下的烃分压，温度T的初始值设置为塔顶温度。

简化烃-水分层计算法考虑了水在烃相的溶解度。为了考察水在烃相的溶解度对计算结果的影响，将图4中计算水在烃相的溶解度这一步骤去掉，即不考虑烃-水之间的相互溶解性，此时体系变为烃-水不互溶体系。表5列出了基于烃-水不互溶假设计算法、简化烃-水分层计算法和严格的三相平衡计算法3种方法的计算结果。从表5可见，基于烃-水不互溶假设计算的水露点温度和对应的气相水分压与简化烃-水分层计算法计算结果一致，说明对于塔顶油气体系，溶解于烃相中的水对气相水分压影响很小；使用严格的三相平衡计算的水露点为384.65 K，与基于游离水假设计算的水露点相差1.3 K。

图4 利用简化烃-水分层计算法计算水露点的流程Fig.4 Calculation procedure of water dew point with hydrocarbon-water layered calculation method表5 3种方法计算的水露点温度结果Table 5 Water dew points derived from three different methods

MethodSteampartialpressure/kPaWaterdewpoint/KHydrocarbon-waterlayeredcalculation144.3383.35Approximationbasedontheimmiscibleassumption144.3383.35Rigorousthreephaseequilibriumcalculation142.1384.65

3 结 论

(1)严格三相平衡计算法通过二元交互作用参数来表征烃-水之间的相互作用，而基于游离水的方法不考虑烃-水之间的相互作用。使用严格的三相平衡计算的水露点为384.65 K，比基于游离水假设计算的水露点高1.3 K。说明烃-水之间的相互作用会对水露点的预测结果产生影响。在炼油厂的实际应用中，需要根据现实的条件来选择是否考虑烃-水之间的相互作用。

(2)对塔顶油气进行严格的三相平衡计算时，烃-水之间的二元交互作用参数kij对水在烃相中的溶解度影响显著，但是对水露点温度的影响不明显。

(3)当假设水相为游离水时，溶解于烃相中的水对气相水分压影响很小，所以可以进一步忽略水在烃相的溶解性，将塔顶油气处理成烃-水不互溶体系。

(4)提出的预测塔顶油气水露点的方法不需要油气体系的详细组成数据，只需要获得石脑油的密度、蒸馏数据等易测得的数据就可以进行计算。2种方法都可以在工程应用中使用。当缺少Aspen等大型模拟软件时，可以使用简化烃-水分层计算法自己编程计算，计算结果能满足实际工程的需要。

符号说明：

a,b,A,B——Peng-Robinson方程参数；

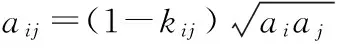
f——逸度；

kij——组分i和j间的二元交互作用参数；

L1——第1液相的摩尔流量，kmol/h；

L2——第2液相的摩尔流量，kmol/h；

LH——液相烃的摩尔流量，kmol/h；

LW——烃相中溶解水的摩尔流量，kmol/h；

m——相数；

MW——相对分子质量；

n——组分数；

NBP——标准沸点，K；

p——压力，kPa；

pc——临界压力，kPa；

pH——烃蒸气分压，kPa；

pW——水蒸气分压，kPa；

pWS——水的饱和蒸气压，kPa；

q(Ethane)——瓦斯流量，kmol/h；

q(Naphtha)——石脑油流量，m3/h；

q(Steam)——水蒸气流量，kg/h；

R——摩尔气体常数，J/(mol·K)；

SG——相对密度；

T——温度，K；

Tc——临界温度，K；

Tr——对比温度，K；

VH——气相烃流量，kmol/h；

v——摩尔体积，m3/mol；

x——摩尔分数；

Z——压缩因子；

ω——偏心因子；

φ——体积分数，%；

φ——逸度系数；

上标:

s——饱和状态；

下标:

H——烃；

i,j——组分；

W——水。

[1] GUTZEIT J. Effect of organic chloride contamination of crude oil on refinery corrosion[C]//Houston: NACE International. Corrosion, 2000: 00694.

[2] SAAB M S, FAQEER F M, Dias O C. Damage Mechanisms and Corrosion Control in a Crude Unit Overhead Line[C]//Houston: NACE International. Corrosion, 2005: 05566.

[3] GUTZEIT J. Controlling Crude Unit Overhead Corrosion-Rules of Thumb for Better Crude Desalting[C]//Houston: NACE International. Corrosion, 2007: 07567.

[4] 倪力军, 张立国, 倪进方, 等. 石油馏分的组成预测初探[J].石油学报 (石油加工)， 1998， 14(2)： 81-85. (NI Lijun, ZHANG Liguo, NI Jinfang, et al. Primary study on prediction of compositions of petroleum fractons[J].Acta Petrolei Sinica (Petroleum Processing Section), 1998, 14(2): 81-85.)

[5] 张利军, 张永刚, 王国清, 等. 石脑油的组成预测方法[J].化工进展, 2011， 30(2)： 278-283. (ZHANG Lijun, ZHANG Yonggang, WANG Guoqing, et al. Research on prediction of naphtha composition based on commercial indices[J].Chemical Industry and Engineering Progress, 2011, 30(2): 278-283.)

[6] 石何武, 白跃华, 董卫刚, 等. 原油虚拟组分划分方法浅析[J].炼油技术与工程, 2009， 39(9)： 61-64. (SHI Hewu, BAI Yuehua, DONG Weigang, et al. Analysis on characterization of pseudo-components of crude oil[J].Petroleum Refinery Engineering, 2009， 39(9): 61-64.)

[7] 韩新宇. 石油馏分描述方法研究进展[J].山东化工, 2015， 44(10)： 51-52． (HAN Xinyu. Research process of the description method of petroleum fractions[J]. Shandong Chemical Industry, 2015, 44(10): 51-52.)

[8] 孙兰义. 化工流程模拟实训-Aspen plus教程[M].北京: 化学工业出版社, 2012.

[9] 陆恩锡, 张慧娟. 化工过程模拟[M].化学工业出版社, 2011: 55-56.

[10] TSONOPOULOS C, WILSON G M. High-temperature mutual solubilities of hydrocarbons and water Part I Benzene, cyclohexane andn-hexane[J].AIChE Journal, 1983, 29(6): 990-999.

[11] ECONOMOU I G, HEIDMAN J L, TSONOPOULOS C, et al. Mutual solubilities of hydrocarbons and water Ⅲ 1-Hexene; 1-octene; C10-C12 hydrocarbons[J].AIChE Journal, 1997, 43(2): 535-546.

[12] DAUBERT T E, DANNER R P. API Technical Data Book-Petroleum Refining[M].Washington D C: American Petroleum Institute (API), 1997.

[13] RENON H, PRAUSNITZ J M. Local compositions in thermodynamic excess functions for liquid mixtures[J].AIChE Journal, 1968, 14(1): 135-144.

[14] 王利生, 郭天民. 基于MPHC活度系数模型关联烃-水体系液-液平衡[J].化学工程， 1996， 24(6)： 59-63. (WANG Lisheng, GUO Tianmin. Correlation of liquid-liquid phase equilibrium for hydrocarbon-water systems based on MPHC activity coefficient model[J].Chemical Engineering, 1996, 24(6): 59-63.)

[15] PENG D Y, ROBINSON D B. Two and three phase equilibrium calculations for systems containing water[J].The Canadian Journal of Chemical Engineering, 1976, 54(5): 595-599.

[16] KABADI V N, DANNER R P. A modified Soave-Redlich-Kwong equation of state for water-hydrocarbon phase equilibria[J].Industrial & Engineering Chemistry Process Design and Development, 1985, 24(3): 537-541.

[17] OLIVEIRA M B, COUTINHO J A P, QUEIMADA A J. Mutual solubilities of hydrocarbons and water with the CPA EoS[J].Fluid Phase Equilibria, 2007, 258(1): 58-66.

[18] LIANG X, TSIVINTZELIS I, KONTOGEORGIS G M. Modeling water containing systems with the simplified PC-SAFT and CPA equations of state[J].Industrial & Engineering Chemistry Research, 2014, 53(37): 14493-14507.

[19] SOAVE G. Equilibrium constants from a modified Redlich-Kwong equation of state[J].Chemical Engineering Science, 1972, 27(6): 1197-1203.

[20] PENG D Y, ROBINSON D B. A new two-constant equation of state[J].Industrial & Engineering Chemistry Fundamentals, 1976, 15(1): 59-64.

Prediction of Water Dew Point in the Overhead Condensing System ofCrude Atmospheric Distillation Unit

OUYANG Wenbin1, HU Haijun1, WU Wei1, LI Xinyun2， ZHANG Yaoheng2, CHENG Guangxu1

(1.SchoolofChemicalEngineeringandTechnology，Xi’anJiaotongUniversity，Xi’an710049，China；2.ResearchInstitute，LanzhouPetrochemicalCompanyofCNPC，Lanzhou730060，China)

On the basis of the relative density and distillation data of naphtha, a series of pseudo-components were yielded by Aspen Plus. The normal boiling point, relative density, relative molecular mass and mole fraction of each pseudo-component were calculated, and the critical properties and acentric factor were estimated by using the corresponding correlation equations with Aspen Plus. With the use of Peng-Robinson equation of state, rigorous three phase equilibrium calculation on gaseous oil fraction of crude atmospheric distillation column overhead system was implemented and the effects of the binary interaction parameters(BIPs) between hydrocarbon and water on water dew point(WDP) and the solubility of water in the hydrocarbon phase were studied. Assuming that the formed water phase of overhead gaseous oil system was free water, the effects of the BIPs between hydrocarbon and water on WDP were researched. The results showed that the BIPs between hydrocarbon and water have great influence on the solubility of water in the hydrocarbon phase. When the BIP was 0.43, the calculated solubility of water was in great agreement with the calculated value by API data book. The solubility of water in the hydrocarbon phase has little influence on WDP. The WDP by rigorous three phase equilibrium calculation was 384.65 K, 1.3 K higher than the computed result based on free water assumption.

overhead condensing system of crude atmospheric distillation column； overhead gaseous oil； water dew point； pseudo-component； Peng-Robinson (PR) equation of state

2016-04-13

中国石油天然气股份有限公司项目(20151191)资助

欧阳文彬，男，硕士，从事过程系统可靠性与风险分析研究；E-mail：wb493805229@163.com

胡海军，男，讲师，博士，从事过程系统可靠性与风险分析研究；E-mail：huhaijun@mail.xjtu.edu.cn

1001-8719(2017)01-0124-07

TE624

A

10.3969/j.issn.1001-8719.2017.01.017