问思教学法在高职数学中的解题探索

程亚芳

(江苏省江阴中等专业学校 214400)

一、生生问思解题探索

问思教学法受制于启发式教学，往往在教学手段和环境方面缺乏一定的新意，笔者思考在教学手段上给予一定的改进，在复习课教学、试卷讲评等环节中，笔者挑选部分优秀的学生进行指导，让课堂从学生的视角作出问和思，获得更好的教学效果．

案例 曲线y=x3上过点(1,1)的切线与两坐标轴围成的三角形的面积为____．

分析1 本题是笔者在导数教学中给学生的一道切线问题，大部分学生的解答是如下：

学生对上述解答并未有异议，甚至不少学生坚持其正确性，笔者请做得正确的学生进行思路上的问和思．

生问：一开始我也是这样想的，但是请同学们对比这两个问题的不同之处：

(1)曲线y=x3上过点(1,1)的切线与两坐标轴围成的三角形的面积为____．

(2)曲线y=x3上在点(1,1)的切线与两坐标轴围成的三角形的面积为____．

生思：这两个问题最大的区别在于一个字“过”和“在”的使用，细细体会是有很大的区别的．如图1，在某一点处的切线，意指在这个点必须是切点；而如图2，过某一点的切线有两个含义，第一层含义即这个点是切点，第二层含义是曲线y=x3有一条切线，恰恰好从点(1,1)过，但点(1,1)并不是切点！

师：请你帮大家演算试试，如何找到这条线？

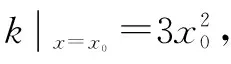
二、师生问思解题探索

有些问题难度较大，采用生生问思方式不太合适，笔者认为根据实际情况需要教师在教学中调整手段，采用师生问思教学法来解决．

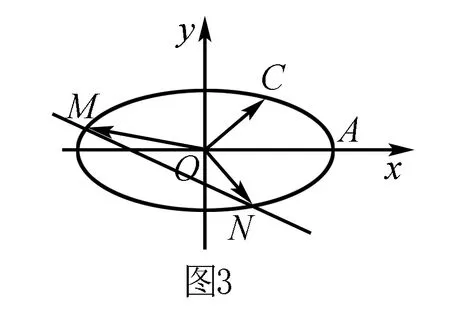
生：从结构来看，应该是运用韦达定理．

师：韦达定理是如何在直线和椭圆位置关系中去寻找的？

生：将直线方程和椭圆方程进行联立，可以获得所需的韦达定理．

师：请大家动手试试．

师：观察韦达定理的两个等式，怎么处理消元？

师：好！接下来计算三角形面积，从计算什么入手？

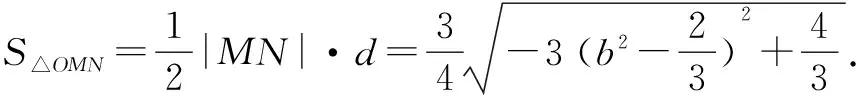
师：直线和椭圆位置关系的判断，从代数角度是如何思考的？

生：用直线方程和椭圆方程联立，通过判别二次方程判别式来判断位置关系，即交点个数．

师：本题中直线MN需和椭圆有两个公共点，因此要注意什么？

说明：对于高职生来说，本题的计算量非常之大，函数模型的最值处理也较为困难，笔者采用教师问思教学手段，将问题以逐步分解的方式层层引导，激发了高职生思考问题的层次性，并且在边问边思中将问题简洁高效地进行了解决，符合学生认知心理．

[1]黄严生,束从武.例谈“问思”教学法[J].中学数学教学,2013(1).

[2]周立志.巧用课堂教学中的典型错误提升课堂效率的若干策略[J].中学数学教研,2013(4).