汤河水库坝体沉陷过程规律探析

朱化平

（辽宁省汤河水库管理局，辽宁辽阳111000）

汤河水库坝体沉陷过程规律探析

朱化平

（辽宁省汤河水库管理局，辽宁辽阳111000）

本文结合汤河水库坝体多年实测的沉陷数据，应用数理统计的方法对水库坝体的沉陷过程进行了回归计算，分析相关性，选取最优曲线，为分析坝体变形规律提供依据。

坝体沉陷；数理统计；回归计算；规律；汤河水库

1 概述

汤河水库坝体为黏土斜墙砂壳坝，分别在防浪墙和坝体背水坡共布设17个观测点，用于观测坝体沉陷量。其中防浪墙上8个观测点，即C1-C8；坝体背水坡在桩号为0+100 m、0+220 m和0+340 m，高程为108.5，98.5，87.5 m的3个平台上，共计9个观测点，即B1-B9。汤河水库每年于汛前、汛后进行坝体沉陷观测各1次，计算出坝体间隔沉陷量和累计沉陷量。

通过多年的观测资料发现，坝体初期沉陷量较大，沉陷过程曲线较陡，后期沉陷逐渐减小，沉陷过程曲线变化平缓，坝体沉陷趋于稳定，该情况符合土坝沉陷过程的一般规律。为了进一步探讨汤河水库坝体沉陷过程的内在规律，本文结合坝体多年实测的沉陷数据，对坝体沉陷过程回归曲线进行探讨。

2 回归曲线计算

土坝沉陷过程的回归曲线，按定性分析一般有6种类型，根据汤河水库的实测情况初步分析，选取双曲线和对数曲线进行分析和比较，从中选取1条最优回归曲线。

在一元线性回归分析中，回归直线为Y（预i）= A+BX（i），根据最小二乘法原理，设有N个观测值［X（i）-Y（i）］，i=1，2，3，…，N，

使平方和

∑［Y（i）-Y（预i）］2=∑Y［（i）-A-BX（i）］2

为最小的回归直线是最好的，通过求导可得

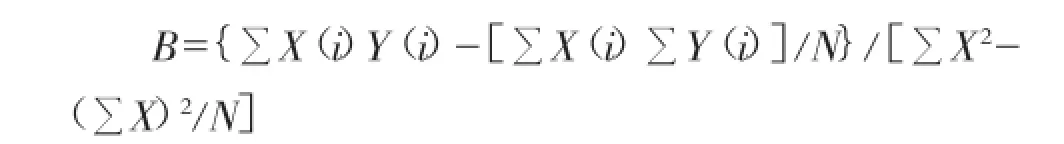
同时B=L（XY）/L（XX）

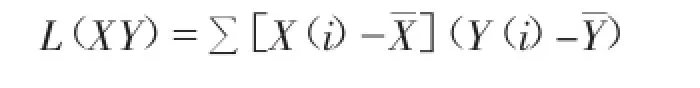
差平方和；L（XY）代表X的离差和Y的离差乘积之和；L（YY）=［Y（i）-Y］2，代表Y的离差平方和。

但是本文研究的土坝沉陷与时间是某种曲线关系，因此必须通过适当的变量代换，将曲线回归化为直线回归。

对于数据曲线H＝A+B/T（H代表沉陷量，mm；T代表历时，d），令Y=H、X=1/T，则Y＝A+BX。

对于双曲线，则1/H=A+B/T，令Y=1/H、X=1/ T，则Y=A+BX。

根据以上思路，对汤河水库17个沉陷观测点进行回归计算，结果见表1。

3 相关分析

土坝沉陷过程的曲线求出以后，为了定量解决曲线是否和实测数据配合的最密切，需要用一个数量指标来衡量配合的密切程度，这个指标就是相关系数R，它能够满足以下3点要求：

1）当所配的曲线为Y＝F（X）是完全符合观测数据，即

Q＝∑［Y（i）-Y（预i）］2＝0

那么希望R=1。

2）当Y与X之间什么关系都不存在时，只能以Y（i）的均值Y做Y的估计值，即Q＝∑［Y（i）-Y］2为最大，这时希望R=0。

3）当0＜∑［Y（i）-Y（预i）］2＜∑［Y（i）-Y］2，希望0＜R＜1，

TV698.2+32

B