基于摄动理论的泥沙群体沉降公式研究
2017-02-05倪志辉牟明艳吴立春
倪志辉,牟明艳,吴立春,赵 健,钟 亮
(1.重庆交通大学 a.水利水运工程教育部重点实验室;b.国家内河航道整治工程技术研究中心;c.西南水运工程科学研究所,重庆 400016;2.重庆第二师范学院,重庆 400067)
基于摄动理论的泥沙群体沉降公式研究
倪志辉1a,1b,1c,牟明艳1a,1b,吴立春2,赵 健1c,钟 亮1a
(1.重庆交通大学 a.水利水运工程教育部重点实验室;b.国家内河航道整治工程技术研究中心;c.西南水运工程科学研究所,重庆 400016;2.重庆第二师范学院,重庆 400067)
国内外许多学者对单个颗粒泥沙沉降公式进行了大量的实验研究和分析,鉴于单个颗粒的沉速与群体沉降可以相差10倍,目前泥沙群体沉降公式大多为经验表达式,因此,深入研究群体颗粒泥沙沉降公式有重要的意义。考虑到在群体泥沙沉降中粗细颗粒粒径大小对泥沙沉降公式的影响,基于摄动理论和最小二乘法,在泥沙群体沉降一般模式的基础上,提出一种新的泥沙群体沉降计算模式。通过对现场实测资料和水槽试验数据进行计算拟合,并与其它经典公式相比较,发现所推导的公式要优于后者。研究结果表明:针对群体泥沙沉降中粗细颗粒粒径大小,考虑其颗粒间的相互影响,按群体泥沙颗粒粒径大小范围分别考虑,是一种群体泥沙沉降计算比较有效的途径。
泥沙群体沉降;沉降公式;摄动理论;最小二乘法;粗细颗粒;单粒沉速
1 研究背景
泥沙沉降是泥沙运动动力学的基本问题之一,一直以来学者对于这部分研究较多[1-6]。多沙河流的浑水泥沙颗粒沉降特性比清水与低含沙的更复杂,其中尤以群体沉降更待细致研究。群体颗粒沉降特性研究的重要意义体现在,单个颗粒的沉速与群体沉降可以相差10倍。多年前就有人说泥沙运动严格地讲只有一个半理论[2]。因而需进一步分析泥沙群体沉降规律,使其在实际应用中不致有太大的误差。泥沙群体沉速公式多为经验表达式,其对沉速与各物理量间的关系以及群体沉降运动的阻力规律表达不明确,这正是该问题研究的不足之处[7-8]。所有沉降现象的研究目标都是建立准确的沉速表达式,在此过程中沉降运动阻力系数表达式的建立成为解决问题的瓶颈。
2 同类公式的对比与讨论
现有的泥沙群体沉速公式大致可分为2种类型。一种是以决定群体沉速的各主要影响因子为变量,直接给出群体沉速的数学表达式;另一种较为多见的是以群体沉速与泥沙单颗沉速的相对比为量值,建立其与主要影响因子的关系,从而得到群体沉速表达式。由于沉降运动阻力系数的表达式未能很好地解决,因此所能见到的泥沙群体沉速公式绝大多数是以ω/ω0这一相对值的形式出现,且基本上以经验公式为主[9]。其中最为广泛采用的群体沉降无量纲公式为ω=ω0(1-βSv)m,是针对浑液紊团的群体沉降提出的无量纲公式[10]。
许多研究成果[1-5]均表明,对于生产实际中的非均匀沙群体沉降问题,可通过对泥沙颗粒级配的分级,先通过试验测试特定颗粒所形成的浑水体的黏滞系数,进而利用其确定相关物理量。重度相同的颗粒沉速研究结果表明,颗粒的大小决定了其沉降时的绕流流态,使得粗细颗粒的沉降遵循不同的规律。
前人提出群体泥沙沉降的公式大致有以下几种。
(1) Batchelor[11]认为球体在低含沙水体中沉降时,颗粒间及颗粒与周围水体相互影响,其沉速与在清水中沉速的差异,是平均值不为0的随机变量。他从统计理论出发,最后推导出低含沙量情况下群体沉速的理论公式,即
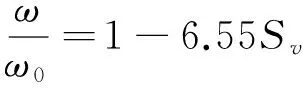
(1)
式中:ω及ω0分别是固体颗粒在浑水中的群体沉速及在清水中的单颗粒沉速;Sv是体积比含沙量。
式(1)中当Sv≤0.05时,计算结果与试验值基本符合;当Sv较大则偏差大。这大大影响了公式的适用范围。
(2) Richardson和Zaki[12]采用量纲分析与试验结果,建立群体沉速公式[12],即
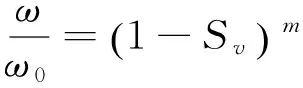
(2)
式中:指数m与沙粒雷诺数(Red=ω0d/ν)有关;d为沙粒粒径;ν为黏滞系数。夏震寰和汪岗[13]对细沙取m=7时,上式与试验资料符合较好。
(3) 张红武等[3]在沙玉清公式[6]基础上,考虑到沉降过程中一部分清水将依附沙粒同时下沉,结合试验结果,经推导得出群体沉速公式[2],即

(3)
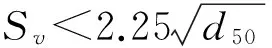
(4) 张耀哲[14]总结了前人的研究后得出Re=ρ1ωd/(6μSv)和Cd=(ρ2-ρ1)(1-Sv)3gd/(6ρ1Sv),以及其推导出的公式为

(4)
(5) 有人认为细的单颗粒泥沙在清水中下沉时有(γs-γ)πd3/6=3πdμ0ω0,μ0为清水黏度;γs为干重度。当为浑水时,上式仍成立,不过应以μm代替μ0,γs代替γ,ωs/(1-Sv)代替ω0。浑水黏度采用日本森氏公式μm/μ0=1+3Sv/(1-Sv/0.52),代入式(4)可得群体沉速公式[8],即

(5)
群体沉降公式在理论上要尽量合理,尽可能地有严格的两相流体力学的依据,量纲上要和谐,同时计算结果要与实测资料基本符合,才可用于实际计算。
3 研究方法
3.1 摄动理论介绍
摄动理论是在求解带小参数的非线性方程的基础上逐渐发展起来的。它不同于常用的迭代法,因为建立在摄动理论基础上的渐近法主要是求解预先展开为小参数的级数,因此将原来的问题转化为逐步求解展开式的各项系数,从而逐步的逼近真值,这样做比求解原来的方程要容易些,一般情况下都能解出。
采用摄动理论进行求解时,首先要对方程无量纲化,提出小参数,即摄动变量。摄动法将解表现为渐进级数,摄动解是对基本解阶数越来越高的逐步微量修正。
主要步骤就是对影响因子p进行无量纲化,引进小参数ε,然后对影响因子p进行摄动,可得
p=p0+εp1+ε2p2+… 。
由于渐进级数的渐进性,往往取少数几项精度就相当高,有时甚至能达到精确解。目前通常都取摄动解式的一阶或者二阶。
3.2 公式推导
从影响沉降的因素来看,阻力系数公式是难以直观表达出来的,因而我们着重考虑在泥沙粒径上探寻方法。在自然河流中泥沙沉降时颗粒粒径是并不相同的,存在粗细颗粒杂陈的模式,因而试着考虑用颗粒粒径来确定公式的使用范围。本文拟用此种方式来间接地表达出颗粒对阻力的影响。在现有研究的群体沉降公式中,最为广泛采用的2个无量纲式是ω=ω0(1-Sv)n和ω=ω0(1-βSv)m,ω=ω0(1-Sv)n是Richardson和Zaki[12]针对单颗粒沙提出的无量纲式,而ω=ω0(1-βSv)m是针对浑液紊团的群体沉降提出的无量纲式,两式针对的对象并不相同,放在一起是为了同时兼顾在自然状况下颗粒粒径不同的情况。引入摄动理论可将沉降表达成如下的无量纲式

(6)
根据国内外的研究成果可以发现,其实很多由天然河道得出的经验或者半经验公式的基本表达式就是这样。本文主要研究的方面是天然河道中非均匀沙层流的情况。
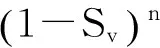
对初始沉速ω0与(1-Sv)n的对比关系采用摄动理论,可得
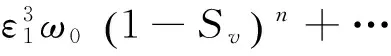
(7)
式中ε1为摄动变量。
对初始沉速ω0与(1-βSv)m的对比关系采用摄动理论,可得

(8)
式中ε2为摄动变量。

将两式相加可得
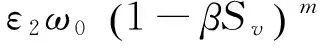
(9)
为了表示更为直观,现用k1代替ε1,用k2代替ε2,用k3代替ω1+ω2,整理上式可得

(10)
3.3 物理量的确定
根据前人的经验成果,并考虑公式的适用性,可按粗砂与细砂的差别来针对指数范围作初步的分析。
粗砂与细砂的判别标准即0.2 mm以下为细砂,0.2~2 mm为粗砂,2 mm以上为砾石。根据前人研究对粗细颗粒的分别判断,现为指数确定了大致范围。当d≤0.2 mm时,6
由式(10)可知,此公式的未知数为3个(k1,k2和k3),但在一般情况下,实测数据不一定是3层。因此,本文考虑采用最小二乘法(文献[15]和文献[16]也应用了该方法)进行求解,具体步骤如下:

表1 前人现场实测成果资料
注:V为河道平均流速;H为河道平均水深;S*为河道平均含沙量。
(1) 建立目标函数,即

(11)
式中Svi和ωi分别表示第i层的含沙量和沉速。
(2) 当目标函数取极小值时满足:
式中l代表拟合的点数。通过矩阵求解,即可解出k1,k2和k3的值。
基于最小二乘法原理对国内外随机的1 136场实测资料(见表1)进行线性回归分析,因涉及指数分析,在此采用了Origin对实测资料进行线性回归分析,并根据不同的粒径采用了不同的分析公式。由此,推导的沉降方程为:
(12)
式中:ω为平均沉速(mm/s);ω0为初始沉速(mm/s)。
式(12)即是本文推导的群体泥沙沉降公式。
4 数据验证与比较
4.1 天然实测资料验证
天然河道包括美国的奈厄布拉勒河、阿查法拉亚河、里奥格兰德河、密苏里河、萨克拉门托河、肘河以及哥伦比亚的河流等[21-24]。奈厄布拉勒河发源于怀俄明州拉斯克附近,东流在内布拉斯加州奈厄布拉勒村注入密苏里河,全长720 km,流域面积达31 080 km2[17]; 阿查法拉亚河是美国红河和密西西比河支流,源于路易斯安那州中部,全长360 km[18]; 密苏里河是美国主要河流之一密西西比河最长的支流,发源于蒙大拿州黄石公园附近的落基山脉东坡,流至密苏里州圣路易斯以北汇入密西西比河,全长4 300多公里[19]; 萨克拉门托河是美国加利福尼亚州最长的河流,该河发源于卡斯克德山脉的沙斯特山附近,全长614.8 km[20];里奥格兰德河长约合3 033 km,从科罗拉多州西南部流入墨西哥湾,流经得克萨斯州和墨西哥边境的大部分地方[20]。
由于实测资料大多没有初始沉速ω0,故根据相对应的中值粒径d50采用斯托克斯公式以及沙玉清公式推导得出初始沉速公式为
(13)
为验证推导公式的可靠性,本文也将采用剩余的1 000场天然实测数据资料进行公式的验证。各公式验证结果如图1所示。
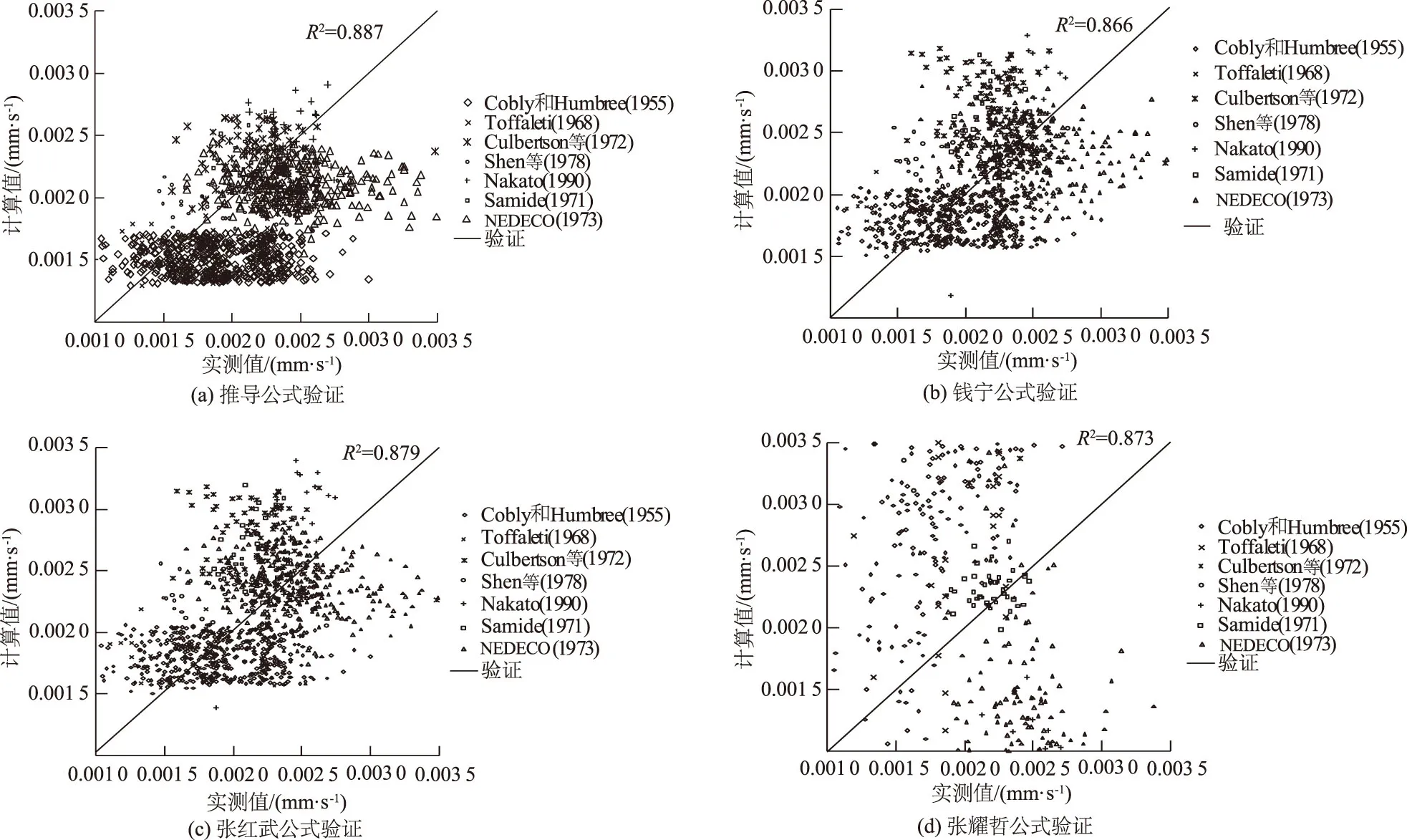
图1 本文推导公式现场实测资料验证及与各家公式比较
根据图1中的验证结果可知:相比于钱宁公式、张红武公式以及张耀哲公式,推导公式和钱宁公式
的拟合度均高。结合各个公式的理论依据,我们不难发现,拟合度高的万兆惠公式引入的是浑水度,而推导公式则是将粗细颗粒的差别表达出来,由此可得出,在各个公式中,对粗细颗粒引起清水改变量是比较关键的因素。
4.2 水槽试验成果验证
为了完整验证本公式的可靠度,本文将采用Meyer-Peter和Muller的水槽试验,其试验根据泥沙粒径的不同,分别做了3组试验[4]。当粒径在0.52~5.2 mm时,对应的水槽宽度为0.353 9 m;当粒径为3.3 mm时,水槽对应的宽度为0.499 9 m;当粒径在0.38~28.65 mm时,对应的水槽宽度为1.999 8 m;Einstein水槽试验,其水槽的水槽宽度为0.266 7 m,相对应的泥沙粒径范围为0.11~0.91 mm[4];Einstein-Chien[25]水槽试验的水槽宽度为0.304 8 m,对应的泥沙粒径范围为0.095~0.385 mm;Brooks[26]水槽试验的水槽宽度为0.266 7 m,其试验的泥沙粒径为0.088~0.145 mm;Song等[27]水槽试验的水槽宽度为0.599 8 m,泥沙的粒径为12.3 mm以及王兆印等[28]水槽试验的水槽宽度为0.5 m,对应的泥沙粒径为0.18~13 mm。对水槽试验的成果进行进一步的验证分析,其数据统计范围见表2。
试验成果的验证如图2所示。

表2 试验成果水力因素的范围
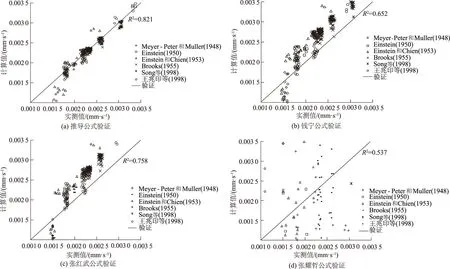
图2 本文推导公式水槽试验数据验证及与各家公式比较
4.3 误差对比分析
基于现场实测资料和水槽试验数据,对以上验证结果进行误差分析,见表3。
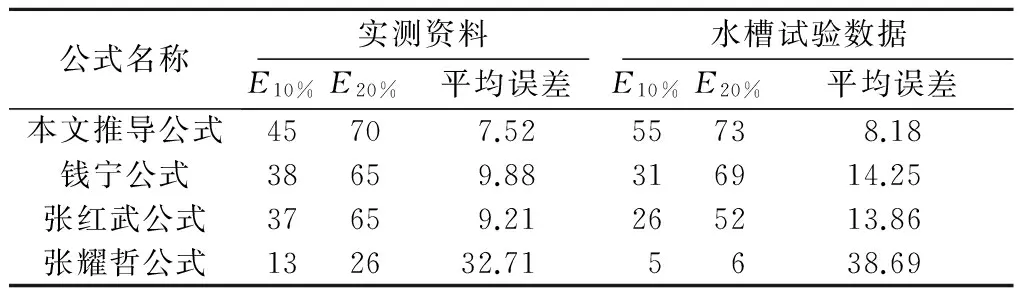
表3 各公式的误差分析
注:E10%为误差小于10%的散点所占的比率;E20%为误差小于20%的散点所占的比率。
从表3中不难看出,无论是实测资料验证还是水槽试验数据验证,本文推导公式能反映泥沙群体沉降运动的一般规律。该公式由于考虑了粗细颗粒的粒径分段,能更好地符合验证资料。
将本文推导沉速公式应用在不同的河流,得到公式在每条河流的拟合系数,见表4。从表4可知,推导公式的相关系数最高可达0.931,且对各条河流的相关性较高于其它公式。由于本文推导公式和张红武公式均对粗细颗粒进行了粒径大小的考虑,从而得到相关系数比未考虑粒径的其它公式要高,这就说明考虑粗细颗粒粒径,可以提高泥沙沉速公式的合理性。本文推导公式由于对泥沙粗细颗粒的粒径进行了分段处理,因此进一步使得沉降公式计算更符合实际。

表4 4各公式相对应的河流R2值
5 结 论
本文考虑到在群体泥沙沉降中粗细颗粒粒径大小对泥沙沉降公式的不同影响,基于摄动理论和最小二乘法,在泥沙群体沉降一般模式的基础上,采用无量纲式因次分析的方法,提出一种新的泥沙群体沉降计算模式。通过对现场实测资料和水槽试验数据进行计算拟合,得出如下结论:
(1) 本文推导沉速公式应用在不同的河流,较钱宁公式、张红武公式和张耀哲公式更接近实测资料,精度更高。
(2) 针对群体泥沙沉降中粗细颗粒粒径大小各异,考虑其颗粒间的相互影响,按群体泥沙颗粒粒径大小范围分别考虑,使计算的结果更为合理。
(3) 本文是基于摄动理论和最小二乘法等应用数学方法在泥沙群体沉降公式中的应用探讨,推导公式中一些参数缺乏明显的物理意义。因此,需要作进一步深入的研究,以便于在工程实际中能更准确地应用。
[1] 张瑞瑾,谢鉴衡,王明甫,等.河流泥沙动力学[M].北京:水利电力出版社,1989.
[2] 郑邦民,夏军强.固体颗粒群体沉降速度分析[J].泥沙研究,2004,(6):23-27.
[3] 张红武,江恩惠,白咏梅,等.黄河高含沙洪水模型的相似律[M].郑州:河南科学技术出版社,1994.
[4] 钱 宁,万兆惠.泥沙运动力学[M].北京:科学出版社,1983.
[5] 中国水利学会泥沙专业委员会.泥沙手册[M].北京:环境出版社,1988.
[6] 沙玉清.泥沙运动学引论[M].西安:陕西科学技术出版社,1996.
[7] 张兴荣.粉煤灰静水群体沉降特性研究[R].武汉:武汉水利电力学院泥沙研究室,1989.
[8] 山西省水利科学研究所.非均匀沙静水沉降试验研究(阶段报告)[R].太原:山西省水利科学研究所,1978.
[9]曾 浩,任增海.高含沙水流沉降规律和阻力特征[C]∥河流泥沙国际学术讨论会论文集.北京:水利电力出版社,1980.
[10]褚君达.浑水的粘滞性[C]∥河流泥沙国际学术讨论会论文集.北京:水利电力出版社,1980.
[11]BATCHELOR G K J. Sedimentation in a Dilute Dispersion of Spheres[J]. Journal of Fluid Mechanics, 1972, 52(2): 245-268.
[12]RICHARDSON J F, ZAKI W N. Sedimentation and Fluidisation, Part I[J]. Chemical Engineering Research and Design, 1997, 75(Sup.): 82-100.
[13]夏震寰,汪 岗.无粘性均质颗粒在细颗粒悬浮液中的沉降[J].泥沙研究,1982,(1):14-23.
[14]张耀哲. 非粘性均匀沙群体沉降运动沉速公式的研究[J].西北农林科技大学学报,2006,34(4):117-120.
[15]倪志辉, 吴立春, 宋志尧. 近岸海域海面风速分布的预测方法研究[J].空气动力学报, 2010, 24(2): 547-552.
[16]NI Zhi-hui, WU Li-chun, ZHANG Xu-jin,etal. A New Model for the Regulation Width of Waterway Based on Hydraulic Geometry Relation[J]. Mathematical Problems in Engineering. DOI: http:∥dx.doi.org/10.1155/2013/182656.
[17]COBLY B R, HEMBREE C H. Computation of Total Sediment Discharge, Niobrara River near Cody, Nebraska[R]. Washington D.C.: U.S. Geological Survey, 1955.
[18]TOFFALETI F B. A Procedure for Computation of the Total River Sand Discharge and Detailed Distribution, Bed to Surface, Technical Report No.5[R]. USA: Committee of Channel Stabilization, Corps of Engineering, U.S. Army, 1968.
[19]SHEN H W, MELLEMS W J, BARRISON A S. Temperature and Missouri River Stages Near Omaha[J]. Journal of the Hydraulics Division, 1978,104(1):1-20.
[20]NAKATO T. Tests of Selected Sediment-transport Formulas[J]. Journal of Hydraulic Engineering, 1990,116(3):362-379.
[21]SAMIDE G W. Sediment Transport Measurements[D]. Canada: University of Alberta, 1971.
[22]CHITALES S V. Hydraulics of Stable Channels[R].India: Ministy of Irrigation and Power, Central Water and Power Commission, Government of India, 1966.
[23]CHAUDHRY H M, SMITH K V H, VIGIL H. Computation of Sediment Transport in Irrigation Canals[J]. Proceedings of Institution of Civil Engineering, 1970, 45: 74-101.
[24]NEDECO. Rio Magdalena and Canal del Dique Project.Mission Tecnica Colombo-Holandesa[R].The Hague:NEDECO, 1973.
[25]EINSTEIN H A, CHIEN N. Transport of Sediment Mixtures with Large Ranges of Grain Sizes, MRD No. 2[D]. California: University of California, 1953.
[26]BROOKS N H. Mechanics of Streams with Movable Beds of Fine Sand[J]. Transactions of the American Society of Civil Engineers, 1958, 23: 526-549.
[27]SONG T, CHIEW Y M, CHIN C O. Effect of Bed-Load Movement on Flow Friction Factor[J]. Journal of Hydraulic Engineering, ASCE, 1998, 124(2): 165-175.
[28]王兆印, 徐永年, 苏晓波. 挟沙水流的冲刷率及河床惯性的研究[J].泥沙研究,1998, (2):1-9.
(编辑:赵卫兵)
To Determine the Formula of Sediment Group SettlementBased on Perturbation Theory
NI Zhi-hui1,2,3, MOU Ming-yan1,2, WU Li-chun4,ZHAO Jian3,ZHONG Liang1
(1.Key Laboratory of Hydraulic and Waterway Engineering of the Ministry of Education, Chongqing Jiaotong University, Chongqing 400016, China; 2.National Engineering Research Center for Inland Waterway Regulation, Chongqing Jiaotong University, Chongqing 400016, China; 3.Southwestern Research Institute of Water Transportation Engineering, Chongqing Jiaotong University, Chongqing 400016, China;4.Chongqing University of Education, Chongqing 400067, China)
Many scholars in China and abroad have carried out a lot of experimental researches and analysis on the formula of single particle sedimentation. In view of the 10 times difference between single particle sedimentation rate and group settlement, current formulas of sediment settlement are mostly empirical expression. In this paper, based on the perturbation theory and the least square method, a new calculation model for the settlement of sediment group is proposed. The influence of coarse and fine particle sizes are considered. Through calculations and fittings of field measured data and flume experiment data, and compared with other classical formulas, the present model is found to be superior to classical formulas. Results show that taking the sizes of coarse and fine particles into account is an effective way to calculate sediment deposition.
sediment group settlement; formula of sediment settlement; perturbation theory; lease square method; coarse and fine particles; single particle velocity
2015-10-10;
2015-12-02
国家自然科学基金项目(51509026);国家重大水资源高效开发利用专项计划(2016YFC0402104);重庆市基础与前沿研究计划资助项目(cstc2016jcyjA0380);省部共建水利水运工程教育部重点实验室暨国家内河航道整治工程技术研究中心开放基金(SLK2016B03);内河航道整治技术交通行业重点实验室开放基金(NHHD-201514)
倪志辉(1980-),男,湖南衡阳人,副研究员,博士,主要从事河流海岸水动力学、环境及数值模拟方面的研究,(电话)13983642791(电子信箱)benny251@163.com 。
10.11988/ckyyb.20150842
2017,34(1):6-11,18
TV142.1
A
1001-5485(2017)01-0006-06
