定积分和二重积分概念的MATLAB实验教学

2017-02-05郑玉军华玉春汤

湖南科技学院学报 2017年10期

关键词：曲边梯形区间

郑玉军　华玉春汤　琼

郑玉军1华玉春1汤琼2

（1.湖南科技学院理学院，湖南永州 425199；2.湖南工业大学理学院，湖南株洲 412008）

在传统的定积分和二重积分概念教学方式的基础上，进一步运用MATLAB进行辅助实验教学，通过描绘出图形以直观形象的方式解释概念，有助于学生更深入地理解定积分和二重积分的概念，以达到辅助教学的目的。

定积分；二重积分；概念；MATLAB；实验教学

1 引　言

定积分是数学发展中的重要一环，没有定积分的数学可以说是不完整的数学。定积分的作用不仅体现在数学教学和数学研究上，它在许多领域如物理、军事、机械等方面都有着很好的应用。而二重积分的概念又是定积分概念的推广，但对于学生来说，定积分和二重积分的概念却是难于理解的。在此，我们利用MATLAB[1,2]软件做数值实验的方法以直观形象的方式研究定积分和二重积分的概念，有助于学生深入理解定积分和二重积分的概念，从而达到辅助教学的目的。

2　定积分和二重积分概念的MATLAB实验教学

2.1定积分概念的MATLAB实验教学

定积分是数学分析、高等数学、微积分中的重要内容，而教材[3,5-7]几乎都是以求曲边梯形的面积和变速直线运动的路程作为引例，然后抽象出定积分的定义的。在教学中，对定积分概念的介绍，一般也是通过“作分割、近似代替、求和、取极限”四个步骤求曲边梯形的面积(定积分的几何意义就是求曲边梯形的面积)引入的：

（1）作分割：把[]分成个小区间[i-1,x](12)，小区间长度记作△x=x-x1(12)，曲边梯形就分成了个小曲边梯形；

（3）求和：曲边梯形的面积等于个小曲边梯形的面积的和，也近似等于个小矩形的面积的和；

还有一个例子就是求变速直线运动的路程，做法相似，然后可紧接着介绍定积分的定义。

定积分的定义[3,5-6]设函数()在[]上有界，在[]中任意插入若干个分点

012<…<x<x=b,

把区间[]分成个小区间

[0,1],[1,2],…,[n-1,n],

各个小区间的长度依次为

△110△221△x=x-x1,

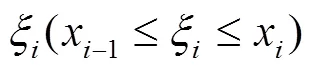
其中()叫做被积函数，()叫做被积表达式，叫做积分变量，叫做积分下限，叫做积分上限，[]叫做积分区间。

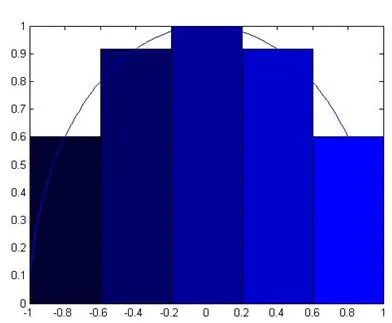
图1.求曲边梯形面积时的图形

尽管如此，学生对定积分的概念仍然模糊不清，存在很多疑问，比如为什么先对区间有限分割后来又要分割得越来越细，为什么是区间的最大长度®0而不是，为什么定积分与区间[]的分法以及的取法无关，等等。即便老师讲解多次，学生仍然疑惑丛生。在教学中，不妨再借助MATLAB数学软件作出具体例子的图形加以解释。如求定积分，即求由曲线和直线11及轴所围成的平面图形的面积。我们将区间[-1,1]均匀分割（实际上可任意分割）成5,10,15,20个小闭区间，在每个小闭区间上都取区间中点（实际上也可取小闭区间上的其它点）的函数值作为小矩形的高，如图1所示。从图1可观察到，当逐渐增大时各个小矩形面积的和与由曲线和直线11及轴所围成的曲边梯形的面积之间的误差越来越小，当无限增大时，各个小矩形面积的和（也即面积和的极限）就是所求曲边梯形的面积（即定积分）。把在每个小闭区间上都取区间中点的函数值换成取区间上其它点的函数值作为小矩形的高，结论相同，说明定积分与的取法无关。这样，以图形直观的方式呈现胜于老师多次费力的讲解，并且有助于学生加深求曲边梯形面积过程的印象和理解定积分的概念。

2.2二重积分概念的MATLAB实验教学

二重积分也是数学分析、高等数学、微积分中的重要内容，教材[4-6,8]几乎都是以求曲顶柱体的体积和平面薄片的质量作为引例，然后抽象出二重积分的定义的。鉴于二重积分的概念是定积分概念的推广，在教学中可用类比法，对定积分和二重积分概念的引入、介绍及几何意义作对比，循序渐进的介绍二重积分的定义。

二重积分的定义[4-6]设()是有界闭区域上的有界函数。将闭区域任意分成个小闭区域△1△2△,

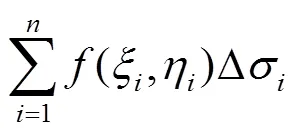
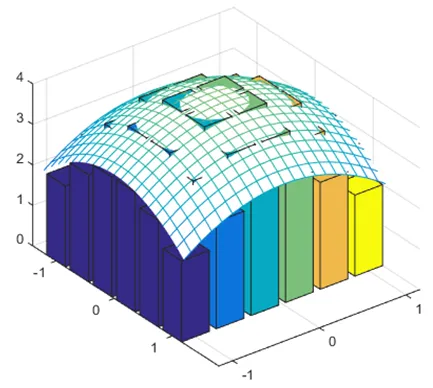
图2.求曲顶柱体体积时的图形

定积分和二重积分概念的定义都是基于微元法的思想，而二重积分的定义是由定积分的定义推广得到的，在计算二重积分的时候又要把二重积分化为定积分来计算。

3　结束语

在传统的定积分和二重积分概念教学方式的基础上，进一步利用MATLAB软件进行辅助实验教学，以图形直观的方式解释概念，有助于学生更深入地理解定积分和二重积分的概念，激发学生学习数学的兴趣，提高学生学习数学的积极性和学习效率，培养学生应用数学知识和数学软件解决实际问题的意识和能力，从而起到辅助教学的作用。

[1]张智星.MATLAB程序设计与应用[M].北京:清华大学出版社,2002.

[2]重庆大学数学系.数学实验[M].北京:科学出版社,2000:1- 25.

[3]同济大学数学系.高等数学(第七版上册)[M].北京:高等教育出版社,2014:224-293.

[4]同济大学数学系.高等数学(第七版下册)[M].北京:高等教育出版社,2014:135-139.

[5]黄浩.高等数学[M].上海:同济大学出版社,2014:107-222.

[6]曹定华,李建平.微积分(第四版)[M].上海:复旦大学出版社, 2011:164-258.

[7]复旦大学数学系.数学分析(第二版上册)[M].北京:高等教育出版社,1983:266-307.

[8]复旦大学数学系.数学分析 (第二版下册)[M].北京:高等教育出版社,1983:246-275.

（责任编校：宫彦军）

2017－02－08

湖南科技学院2016年教学改革研究项目（项目编号XKYJ2016027）。

郑玉军（1982－），男，湖南永州人，讲师，硕士，研究方向为计算数学。