零基线约束的参考站间模糊度固定方法研究
2017-02-05丁乐乐王珍潘宇明李蕾
丁乐乐,王珍,潘宇明,李蕾
(天津勘察院,天津 300191)
0 引 言
北斗地基增强系统是国家统一规划建设的以北斗卫星导航系统(BDS)为主,兼容其他GNSS卫星导航系统的地基增强系统。自2012年我国BDS实现亚太区域定位后,已有多个省市完成了北斗增强系统的升级。目前,基准站升级策略是在原参考站基础上,共用一个天线,增加一台接收机,并且增加单独的数据处理系统,两套数据处理系统的观测数据及服务均未进行融合处理。
参考站间模糊度固定是北斗地基增强系统服务的核心技术[1]。只有快速、准确的固定参考站间整周模糊度,才能实时地为用户提供高精度的误差改正信息。国内外相关学者针对参考站间模糊度固定方法做过许多研究,并且取得了诸多成果[2-5]。主要方法可分为两个方面:1)利用伪距、相位观测数据进行差分或线性组合整周模糊度,最为经典的算法为MW宽巷+窄巷组合确定整周模糊度;2)利用实数模糊度及其方差协方差阵进行矩阵变换,代表性的是最小二乘降相关平差法(LAMBDA)方法。
北斗地基增强系统形成了“一天线+双接收机”的观测模式,每条基线上存两个零基线约束条件,由于零基线双差过程信号传播路径相同,消除了大部分误差,很容易实现模糊度固定。基于此,本文在已有模糊度固定方法的基础上,增加零基线约束条件,进行相应的矩阵变换,以期提高模糊度固定的速度和效率。
1 GNSS双差原始观测方程建立
GNSS双差观测方程形成时,星间差在各自系统内求差。双差观测方程可表示为
λ
λ·ΔεΦ,
(1)
联系人: 丁乐乐 E-mail: dinglelecumt@126.com
一般选取参考星原则为选取卫星高度角最大的卫星作为参考星。某时刻同步观测到m颗GPS卫星和n颗BDS卫星,且分别选择1颗卫星高度角最大的GPS和BDS为各自系统的参考星,形成m+n-2个双差观测方程。
2 模糊度解算参数估计方法
参数估计通常采用扩展Kalman滤波模型。参考站间基线可认为已知,则参数估计主要包括模糊度、对流层延迟。通过使用扩展Kalman滤波,状态向量x和它的方差协方差阵P可以与每个历元tk观测向量yk通过下式估计:
(2)
式中:zk、H、R分别表示量测向量、系数矩阵和观测误差的方差协方差阵。在扩展Kalman滤波中,假定系统模型为线性的,状态方程时间更新和它的方差协方差阵表示如下:
(3)
其中:A为状态转移矩阵;Q为系统噪声的方差协方差。
基于GNSS双差观测模型的卡尔曼滤波状态方程的状态向量x如下:
式中:P0初值为零矩阵; 状态噪声阵Qk的对角阵元素分别为各状态量的方差。由于参考站间基线已知,位置参数的先验过程噪声为0.1 m,双差模糊度参数的过程噪声为20周。大于40 km的基线,状态向量中包含对流层估计参数,对流层延迟过程噪声为0.3 m.电离层延迟误差可通过无电离层模型消除,参数估计中可不估计双差电离层延迟。
观测向量Zk用双差载波和伪距观测值组成:
Zk= (λ1·
Hk为双差观测方程的线性化系数:
假定观测r颗卫星。则系数矩阵中的各项都含有r-1行。E为(r-1)×(r-1)的单位阵。O代表零矩阵。Rk为观测值噪声矩阵,这里假定各颗卫星的观测值之间相互独立,并且设定伪距和载波的标准差分别为σP和σφ.
Kalman滤波获得载波相位模糊度实数值及其方差协方差矩阵后,即可采用整数LAMBDA解算整周模糊度。
3 GNSS参考站间模糊度固定方法
考虑参考站间距在20~70 km,GNSS参考站间模糊度固定策略采用“无线电离层+宽巷模糊度组合”。在中长基线解算时,无电离层组合观测值,消除电离层影响,同时,利用组合系数保持模糊度的整周特性,形成无电离层组合模糊度,构建观测方程可表示为
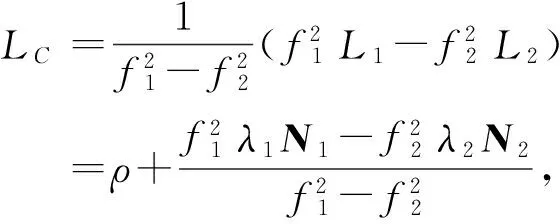
(4)
式中: LC代表无电离层组合观测值; L1、L2为载波原始距离观测值;N1、N2为载波原始相位观测值;f1、f2代表GNSS观测值信号的两个频率,不同卫星系统频率不同;λ1、λ2代表GNSS观测值信号的两个波长;ρ表示卫星到接收机间几何距离;由于双差观测值消除了接收机钟差和卫星钟差,电离层延迟误差也已经消除。对流层误差不能完全消除但能够利用模型映射函数对对流层延迟残差进行估计。
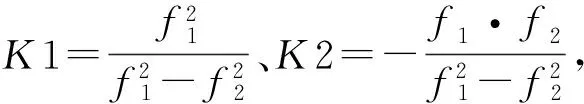
由于宽巷双差整周模糊度具有较长波长,其模糊度相对容易固定,其固定不受基线长短的影响,对低高度角的卫星也不敏感。
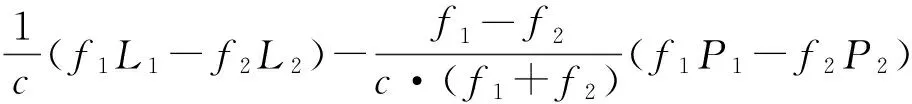
(5)
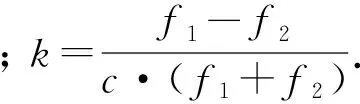
4 基于零基线约束的参考站间模糊度矩阵变换
1) 构建线性变换系数进行变换。
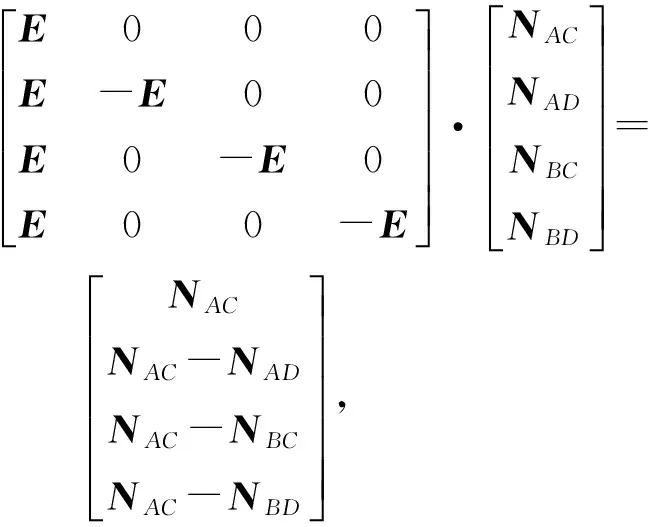
(6)
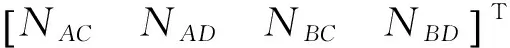
(7)
式中:QZZ为变换后做差模糊度参数;Nzz的方差协方差阵;QAC·ZZ为NAC与Nzz之间的协方差阵。
式(2)变换后的模糊度参数表达为
NAC-NAD=-NCD,
NAC-NBC=NAB,
NAC-NBD=NAB-NCD.
(8)
由于A/B、C/D接收机为同一天线两台接收机的模式,在A与B、C与D之间进行双差时卫星至接收机的电离层延迟、对流层延迟均相同,因此,能够实现A/B、C/D模糊度参数的单历元固定,相应的NAB-NCD能够实现固定。模糊度A/C及其方差协方差更新方程为
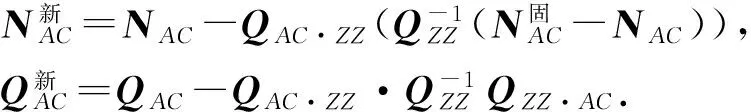
(9)
利用模糊度之间的相关性,修正了NAC模糊度以及NAC模糊度的方差协方差;利用LAMBDA方法进行模糊度固定。
5 数据处理及结果分析
试验选取天津市北斗地基增强系统中的两个参考站KC04和KC09站作为参考试验站,实例数据采用2016年5月1日的天宝接收机和南方接收机1 s数据进行试验,接收机观测数据分别命名为NF04、TB04、NF09、TB09,参考站间距离为60.2 km.读取以上两个参考站四个接收机的观测值数据,对四个接收机的观测数据进行周跳探测等数据预处理。数据处理流程如图1所示。
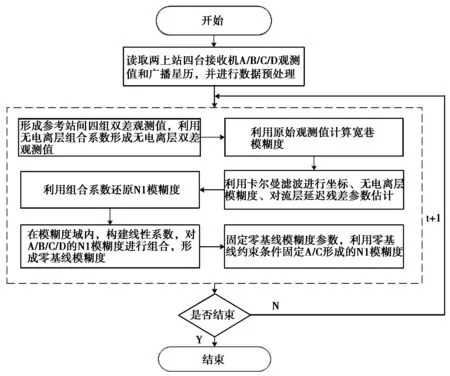
图1 零基线约束的参考站间模糊度计算流程图
按照论文第2、3节,形成无电离层组合观测方程,利用Kalman滤波模型进行参数估计,估计参数为无电离层实数模糊度以及对流层延迟参数。通过第3节给定的系数将无电离层组合模糊度分解为宽巷模糊度和窄巷模糊度;宽巷模糊度对高度角的影响不敏感且易固定,一般通过多历元取均值即可固定。
图2示出了基于观测值直接组合求解的双差浮点宽巷模糊度。从图中可知,只要通过数个历元的平滑即可得到宽巷周周模糊度。通过取整可得到此宽巷模糊度值为2 619 635周。宽巷模糊度一般在几个历元就可以正确固定。
设置观测值的伪距与相位权重比为1∶100,卡尔曼滤波中可以设置坐标状态参数的精度为0.05,模糊度参数的精度设置为20.由于增加了多余观测值,同时包含有零基线约束,收敛过程要快得多。从图3中可知,模糊度正确固定后的整周数为942 774周,零基线多余观测下的参考站间窄巷实数模糊度收敛速度要快得多,收敛结果可以看出,零基线约束条件下的窄巷实数模糊度更接近固定后的整周模糊度。

图2 MW组合双差模糊度实数解
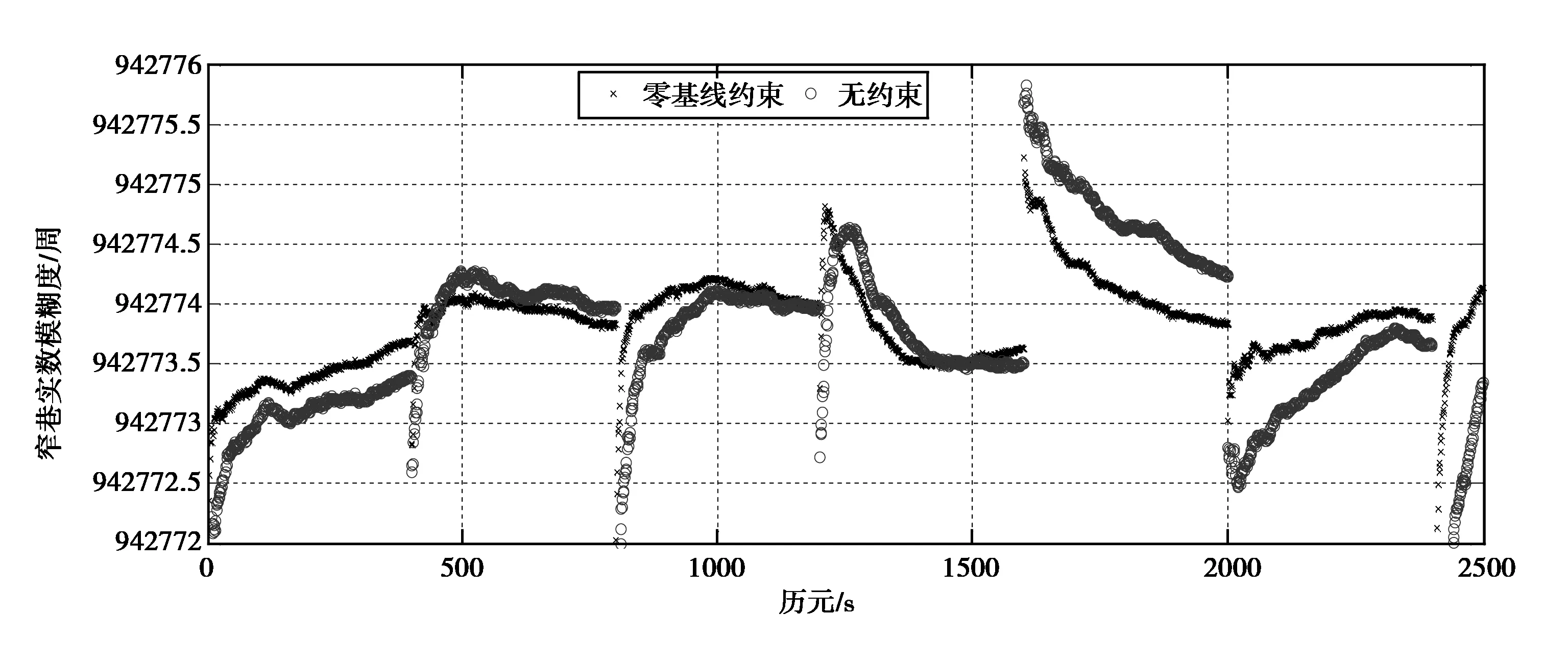
图3 卡尔曼滤波某卫星的窄巷实数模糊度
对流层延迟不能通过观测值组合消除,论文处理方式为模型改正+参数估计的方法消除对流延迟的影响。对流层延迟利用天顶延迟和映射函数模型共同表达,对流层延迟参数按照逐历元进行估计,分为干延迟和湿延迟。逐历元的参数估计结果如图4所示。
在模糊度域内进行线性变换;利用A/C-A/D、A/C-B/C、A/C-B/D线性组合的模糊度单元历元可实现固定的特性,对变换后的模糊度利用LAMBDA方法固定;利用模糊度之间的相关性,用固定的零基线模糊度修正A/C窄巷模糊度实数解及其方差协方差阵;利用LAMBDA方法对A/C窄巷模糊度进行固定。
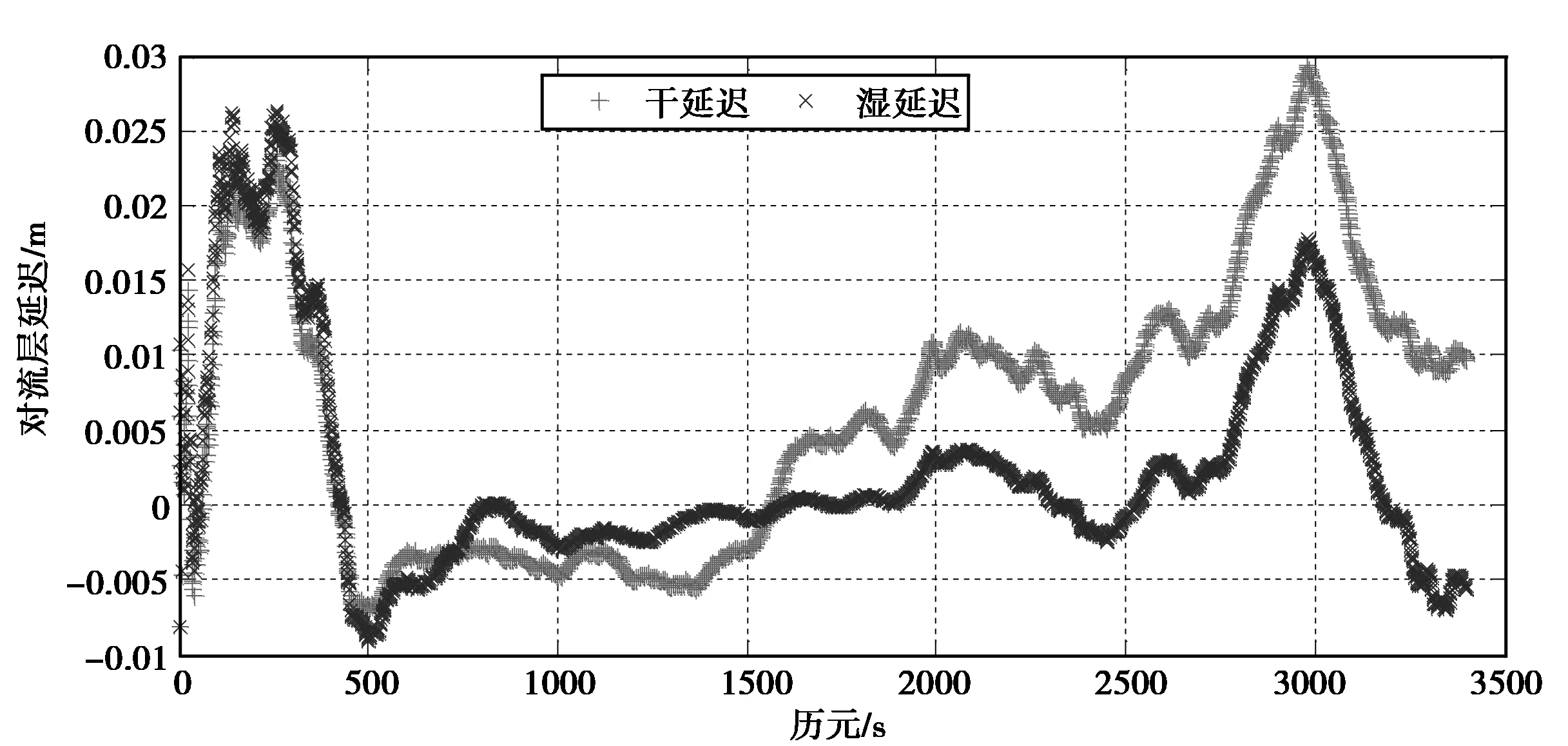
图4 对流层天顶延迟估计结果
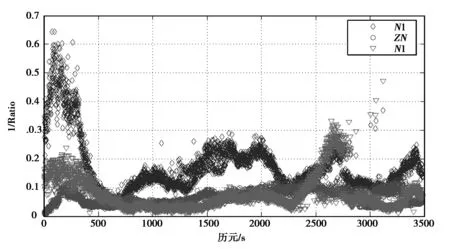
图5 零基线约束模糊度固定与原始模糊度固定Ratio值对比
模糊度固定时的Ratio值对比如图5所示。其中,N1表示分离的模糊度固定时的Raito值,ZN零基线模糊度固定时的Raito值,N1′表示加零基线约束后模糊度固定时的Raito值。从图5中可以看出,零基线参考站间模糊度固定结果较原始的模糊度固定速度和效率有极大的提高。通过统计可以看出,零基线模糊度固定率为100%,原始N1模糊度固定率为95.06%,零基线约束后的模糊度固定率为99.91%.从前500历元看,原始模糊度固定在300历元左右实现固定,固定时间约为5 min.零基线约束后模糊度在第1个历元就已经固定。从初始化速度考虑,零基线参考站间模糊度可以在极短时间里固定。
为进一步零基线约束条件下模糊度固定的比率,选择近6个小时,采样率为1 s的观测数据进行初始化。每60个历元分别采用两种方法固定载波相位模糊度,Ratio阈值设置为2.初始化固定情况如表1所示.由表1可知,零基线约束模糊度固定方法极大地提高了模糊度解算的成功率。
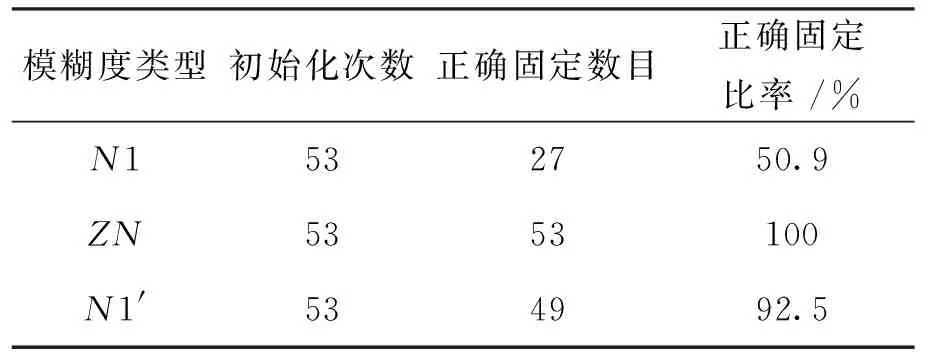
表1 零基线约束模糊度固定统计表
6 结束语
论文论述了GNSS零基线参考站间模糊度快速固定方法,该方法基于“一天线+双接收机”设计进行参考站间模糊度固定,并利用了零基线参考站的观测数据进行模糊度解算,增加了多余观测,将一个天线下的两台接收机观测数据融合处理。同时,利用零基线作为模糊度固定的约束条件,用于解算参考站间模糊度。与传统参考站间模糊度固定方法比,加快了模糊度收敛速度,极大地提高了模糊度固定的速度和成功率。
[1] 李征航,张小红.卫星导航定位新技术及高精度数据处理方法[M].武汉:武汉大学出版社,2009.
[2] 阳仁贵,袁运斌,欧吉坤.相位实时差分技术应用于飞行器交会对接研究[J]. 中国科学:物理学力学天文学,2015,40(5):651-657.
[3] 祝会忠,徐爱功,高猛等.BDS网络RTK中距离参考站整周模糊度单历元解算方法[J].测绘学报,2016,45(1):50-57.
[4] 邓建,王庆,潘树国.网络RTK参考站间低仰角卫星模糊度快速解算方法[J].仪器仪表学报,2010,31(6):1201-1206.
[5] 韩保民,欧吉坤.一种附约束的单频单历元GPS双差相位解算方法[J]. 测绘学报,2002, 31 (4):300-302.
[6] 高星伟,李毓麟,葛茂荣.GPS/GLONASS相位差分的数据处理方法[J].测绘科学,2004,29(2)22-24.
[7] 周乐韬,黄丁发.一种参考站间双差模糊度快速解算策略[J].大地测量与地球动力学,2006,26 (4):34-40.
[8] 罗孝文,欧吉坤.中长基线GPS网络RTK模糊度快速解算的一种新方法[J].武汉大学学报(信息科学版), 2007, 32(2):156-159.
[9] 唐卫明,刘经南,施闯,等.三步法确定网络RTK基准站双差模糊度[J].武汉大学学报(信息科学版), 2007,32 (4):305-308.
[10]李博峰,沈云中,周泽波.中长基线三频GNSS模糊度的快速算法[J]. 测绘学报,2009, 38 (4):296-301.
[11]YANG, Y X, HE H B, XU G C. A new adaptively robust filtering for kinematic geodetic positioning [J]. Journal of Geodesy, 2001,73(2-3): 109-116.
[12]TEUNISSEN P J G, VERHAGEN S.The GNSS ambiguity ratio-test revisited: A better way of using it[J].Survey Review,2009,41(312):138-151.
