“一题多变法”在提高学生数学能力方面的应用
2017-02-04刘峰
刘峰
摘 要:在初中数学教学中,“一题多变法”不仅能帮助学生巩固和灵活运用所学知识,并且能拓宽学生知识视野,掌握新知、探索旧知、提高学生数学思维能力的作用。
关键词:一题多变;思维能力;应用
日常教学中,在以下几个方面应用“一题多变法”,对提高学生数学能力起到很好的效果
一、改变数字,强化学生对知识的掌握和巩固
在新课讲授时,要注重教学设计,每堂课要精心设计课堂练习。为了强化学生对知识的掌握,经常对例题做简单修改,这样对学生来说,降低了知识掌握的难度,增强了模仿性,提高了学生学习的兴趣,并对培养学生“化归思想”有很好的效果。
【例1】(八年级分式方程)两个工程队共同参与了一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,求乙队的施工速度?
在设计课堂练习时,我把题目改变了一些数字:
【课堂练习】两个工程队共同参与了一项筑路工程,甲队单独施工1个月完成总工程的五分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,求乙队的施工速度?
这种改变的仅仅是数字和方程,不变的是解题思路、相等关系。学生理解起来更容易,参与的程度更高,教师再从旁引导,比较练习题和例题之间的联系和区别,引导学生探索在应用题中如何根据相等关系列方程,进一步提高学生的解题能力。
二、改变题目的问法,活跃学生的数学思维
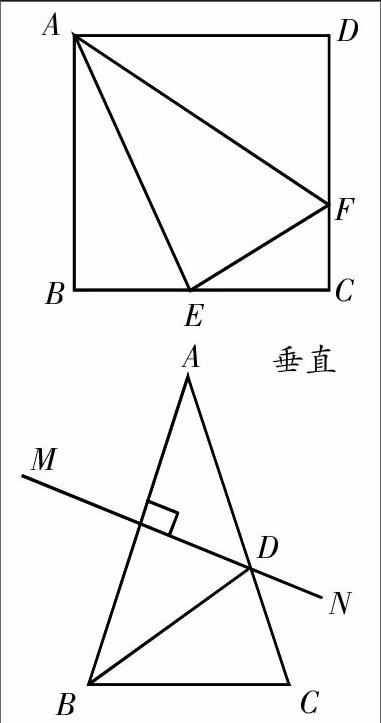
【例2】如图:在正方形ABCD中,点E是BC边上的点,EF⊥AE交CD于点F。求证:当E是BC中点时,△ABE∽△AEF
例题讲解一个星期后,我把题目作了些变化,以作业的形式布置了下面练习。
【变化后的例2】在正方形ABCD中,点E是BC边上的动点,EF⊥AE交CD于点F。
求证:当E在BC的什么位置时,△ABE∽△AEF
原题是一个封闭题,把求证部分变成:当E在BC的什么位置时,△ABE∽△AEF后,题目变成了一个开放题,这就要求学生在对所学知识有很好的掌握后,改变思维方式;改变后的题目也从原来的一种思维方式,变成了两种思维方式:(1)学生可以先找出E点的位置,再进行三角形相似的证明。(2)学生可以把三角形相似当成已知条件,找出符合条件的E点。
这种教学方法,我在教学中使用的频率很高。经过教学实践检验,这种方法对学生数学能力的提高作用是很大的,对学生数学思维的培养也有很强的效果。
【例3】(八年级垂直平分线)如图,△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,∠A=40°,则∠CBD= 。
在例题讲解后的一次单元测试中,我把这个题目改成了下面的这个题型:
【改变后的例3】△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,∠CBD=30°,则∠A= 。
改变了已知和结论,学生在解题的时候,会发现解题的方法也变了。原题中,只需通过∠A=40°,得到∠ABD=40°,∠ABC=70°∴∠CBD=∠ABC-∠ABD=30°。改变后的题目则需设∠A为x
∴∠ABD=x,∠ABC=∠C=x+30°∴x+2(x+30°)=180°,进而求出∠A=40°。这对学生来说,是一种全新的题型,很多学生在做完后,都有一种难言的喜悦。在这个题目的解题过程中,学生收获良多。
在初中数学教学中,除了上面所举的例子,“一题多变法”的所用范围是很广的。在教学设计过程中,我们适当增加一些“一题多变”,对教学是有很大帮助的。
三、灵活运用“一题多变”,努力提高教学效果
1.适时的引导。如例1这种题型,在练习讲解时,我们可以适当引导,让学生进行总结和比较,强化学生对知识的巩固,并适当进行“化归思想”的培养。
2.适当的时间间隔。如例2,这种题型不适合安排在课堂练习中,应该有一定的时间间隔。教学实践证明,时间间隔在7~10天为最佳,我一般把这种改变后的题型放在单元测验中,或者放在复习课上。
3.必要的强化和巩固。如例3这种题型,随着时间的流逝,很多知识都会有一定遗忘。学生的记忆和知识的掌握,都要求我们在教学过程中进行必要的强化和巩固,我们可以在后期的教学实践中,适当回忆以前讲过的几种题型,这对学生的学习是很有帮助的。
在教学中,我常和学生交流,学生对这种教学方法很喜爱。通过教学实践检验证明,“一题多变法”在教学中的效果是值得我们关注和利用的。
参考文献:
[1]孙琳琳.试论如何在高中数学教学中高效运用一题多变教学法[J].数学学习与研究,2015.
[2]贾湘彬.浅谈一题多解与一题多变在高中数学学习中的运用[J].中学生数理(化学研版),2014.
