基于DEA/ANP方法的声纳浮标搜潜方案决策模型
2017-02-02范赵鹏金中原
范赵鹏,温 玮,杨 磊,金中原
(1.海军航空大学,山东烟台264001;2.92351部队,海南三亚572000;3.91650部队,广州510000)
声纳浮标是巡逻机主要的探潜装备,具有携带和布放方便,搜潜效率高,阵型多样化和隐蔽性好等优点。[1]由于机载浮标数量有限,海洋环境背景复杂,巡逻机的留空时间等限制会影响搜潜概率。如何选择最有效的搜潜战术,更合理地布放浮标阵型和选择浮标数量就很有意义。而关于反潜装备体系效能评估是提升体系作战能力的重要手段。以反潜作战兵力搜潜有效性、准确性和时效性为主要评估指标项,通过仿真推演,能对反潜兵力配置、装备配置、装备性能、战术战法等进行评估和优化。但反潜作战效能可在时间域、空间域多维度展开,并与反潜兵力配置、装备配置、装备性能、战术战法的相关参数多重关联,仿真算法复杂,指标体系丰富,为方案寻优带来挑战。
DEA(Data Envelopment Analysis)理论于1978年提出,运用同类决策单元DMU进行有效性的评价,对工程效率的概念进行了推广,将单输入单输出扩展到多输入多输出。DEA理论算法简洁,误差较低,且排除了主观因素,但不能反映指挥员对搜索概率偏好的程度。网络层次分析法(ANP)经建立具有网络结构的组合分析模型,可明确地反映和量化出各目标、因素、方案间的复杂关系,通过专家评判,可加入决策者主观偏好,是解决此类问题的较好方法。但在解决实际决策问题的过程中,ANP的计算过于复杂不易量化。[2]国内学者运用DEA理论提出了ANP/BOCR评价值新方法,对ANP模型做过许多研究与优化改进,用集成方法解决了问题并证明了决策的科学性。[3]
在反潜巡逻机应召搜潜效能评估中,声纳浮标搜潜方案选择中决策者不仅仅需要让搜潜概率最高,更要考虑装备水平、情报能力、人员水平、战术战法等因素。因此,提出DEA/ANP相结合的新方法充分尊重了决策者的主观意愿,同时具有较强的客观性。
1 建立决策指标体系
1.1 反潜作战搜潜方案两级结构
目前装备使用的航空搜潜设备分为声学和非声学探测。声学探测设备主要有吊放声纳和声纳浮标;非声探测有机载雷达、磁力探测仪、电磁探测仪、红外探测仪、激光探测仪、废气探测仪、核辐射探测仪等。反潜指挥决策模型在决策功能上首先解决装备体系的应用与组合。本文研究的浮标搜潜方案是选择声纳浮标方案后如何选择浮标阵型。在一级搜潜方案选择中,如图1所示,主要列举5种进行讨论。[4]
反潜巡逻机使用浮标布阵的依据是为了得到较高的搜潜效能,即使用较少的浮标、较少的时间而且能获得较高的搜潜概率。布阵决策的具体内容包括如何选定浮标阵型,主要以直线阵、折线阵、三角阵、圆形阵和方形阵,见图2。根据作战任务,对潜艇的感知信息,将被动浮标布放为不同的阵型、不同间距的浮标阵,实现对潜的搜索、定位、跟踪。
1.2 ANP决策指标体系
ANP评价指标分为一级航空搜潜模型指标体系和二级浮标搜潜方案指标体系,见表1、2。
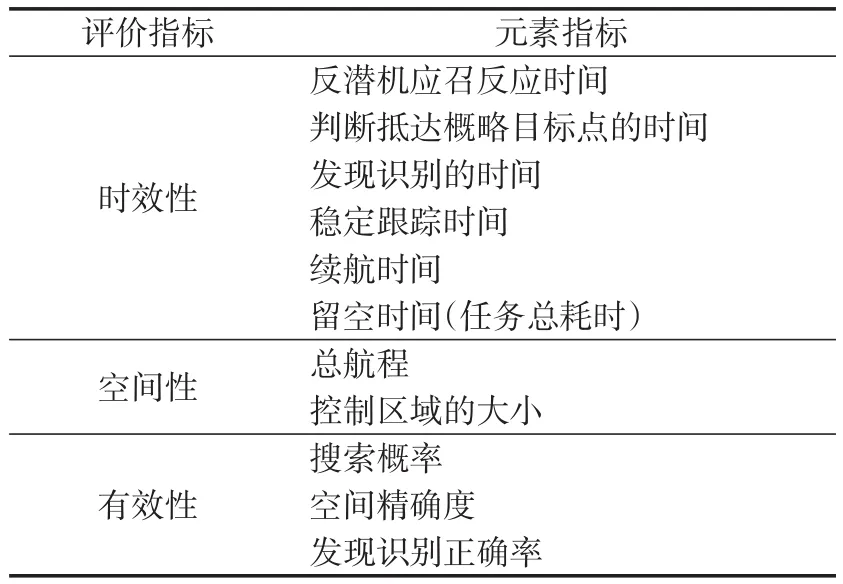
表1 航空搜潜模型指标体系Tab.1 Index system of aerial search model

表2 浮标搜潜方案因素影响指标Tab.2 Factors affecting the search plan of buoy
1.3 DEA决策指标体系
将指标体系划分为只有输入变量和输出变量的数据包络形式。在一级搜索方案选择结构中,输入是战场环境(空间性、时效性)及潜艇目标态势,输出是应用航空雷达搜潜、红外搜潜、吊放声纳搜潜、声纳浮标搜潜、磁探仪搜潜或者是几种方式组合搜潜的方式。二级搜索方案结构中输入是一级方案中影响装备的性能、指挥控制能力、人员水平、单机任务的指标体系因素,输出为发现潜艇的概率。
2 构建DEA/ANP评价模型
2.1 DEA模型的C2R评价模型
DEA的C2R模型由Charnes、Cooper和Rhodes提出的,用于评价DMUk的规模和技术有效性。[5]
DEA方法的数学规划模式是以决策单位DMUk的效率Ek最大化作为目标,寻找对DMUk最有利的投入项权重组合vi1、vi2、vi3、vi4,以及产出项权重组合uj1、uj2、uj3,Xi为决策单元的输入,Yi为决策单元的输出,要使得Ek达到最大值,所有DMUk的效率Ek必须小于等于1。[6]
C2R模式的数学表达式为:
DEA评价模型的分析流程图见图3。
以声纳浮标搜潜方案选择结构为例,反潜巡逻飞机携带的浮标及应召反应的时间均是有限的,简化算法构建决策单元DMU见图4。
定浮标数量为M,飞行时间为t,潜艇发现概率为P。其中决策的单元DMU输入为浮标数量,应召时间,输出为潜艇发现概率。输入信息都可根据资料或测量,输出信息可运用经验公式进行量化。
采用具有非阿基米德无穷小量的模型,[7]其对应的线性规划为:
式(5)中:λj≥0(j=1,2,…,n);;θ代表决策单位DMUk的效率值,相对于其他被评价单元,θ越大说明第j个决策单元的运行效率越高,资源配置状态越趋于合理,越小说明第j个决策单元的运行效率越低;λj表示评估DMUk的相对效率时参考DMUr的比例;表示效率DMUk应减少的投入量;表示效率DMUk应增加的产出量,用模型评价第i个决策单元的有效性,是相对其他决策单元而言的。
2.2 ANP评价模型优化与构建
设一级指标为目标层,对应航空搜潜模型指标体系中的时效性、空间性、有效性,对应浮标搜潜方案中的装备性能、指挥控制、单机任务、人员水平;下级因素为要素层,通过要素之间的相互依存与反馈的关系构造ANP网络层,在ANP工具中对应影响要素,共同构建ANP模型。设研究的问题为A,目标层的元素为Bi(i=1,2,3,4),有3个要素组Ci在网络层,Ci中有要素Cij,其中1,2,…,n,n为要素的个数,则ANP计算过程如下:
1)构建比较判断矩阵。设标度准则为固定的,以要素Cij为影响因素。设定目标层为准则层,对Cij进行间接的比较,以相互间的影响力来确定优势度。[8]
2)通过目标层间要素相互比较得出超矩阵。由第i层对j层的所有要素产生的影响生成矩阵:
通过2个要素间进行相互比较得到向量排序,产生超矩阵的每一列。
3)由判断矩阵计算模型的超矩阵并将矩阵权重化、极限化最终得到加权超矩阵。[9]
4)构造极限超矩阵,通过将加权超阵的若干次幂求解得到,是极限化加权超矩阵。直到每列对应要素均相同的时候极限超阵已经达到稳定。从而得到各要素稳定的归一化权重向量,它可以客观反映各要素间复杂的比较关系。[10]
5)ANP评估模型中按同等、稍重要、明显、强烈、极端、稍不重要、明显不重要、强烈不重要、极端不重要的顺序由专家评判。[11]除1-9标度外,还可由专家手动输入具体分值。采用作战仿真结论与专家意见相结合的方式进行评估并进行专家打分。此时容易出现主观性过强导致评判结果不科学。说明传递矩阵有可能不是最优矩阵,决策者的打分意见需要修正统一。通过计算标准差来判断专家的意见是否合理,如果大于1就将意见分歧较大的专家的评判结果忽略或者让其重新打分,最终辅助决策人员选出最佳方案。
3 声纳浮标搜索阵决策单元评估算例
假定红方预警飞机在巡逻期间雷达发现蓝方潜艇目标,随后蓝方潜艇迅速下潜消失,消失的时间2017年10月17日16:50分,消失点位置为东经120°,北纬38°,预警飞机立即通知反潜巡逻飞机执行应召反潜任务。海上战场态势示意图见图5。
根据战场态势特点,大中型反潜巡逻飞机受机动性能限制,显然不适合选用随机搜索阵搜索潜艇。因此,当使用声纳浮标搜索水下目标时,搜索布阵的图形相对比较规整,决策单元的数量也是有限的。当一级搜潜行动方案集中选择了带有声纳浮标的方案时,根据不同的目标初始散布区域大小和运动信息,可供选择的搜索方案有圆阵、直线阵、折线阵、方阵等。
3.1 运用DEA方法排序
在假定条件中,选用9组常用的声纳浮标阵构成决策单元{DMU1,DMU2,…,DMU9},包括7、9、16枚圆形搜索阵,5、7枚直线拦截阵,7、9枚折线拦截阵,12、15枚矩形搜索阵。通过对方案的时间测算和大样本评估搜索概率,得出指标如表3所示。按表3中数据,采用具有非阿基米德无穷小量的C2R模型公式进行评估。[12]通过Matlab仿真得DEA有效的为DMU4、DMU5、DMU7,即5枚折线阵、7枚直线阵、9枚折线阵为DEA有效。[13]在实际布放过程中,需要考虑的因素很多,虽然根据DEA方法求得了较为客观的浮标搜潜方案,但省略了太多中间影响的因素,忽视了决策者的主观偏好,故最优的布放方案还需进一步讨论。
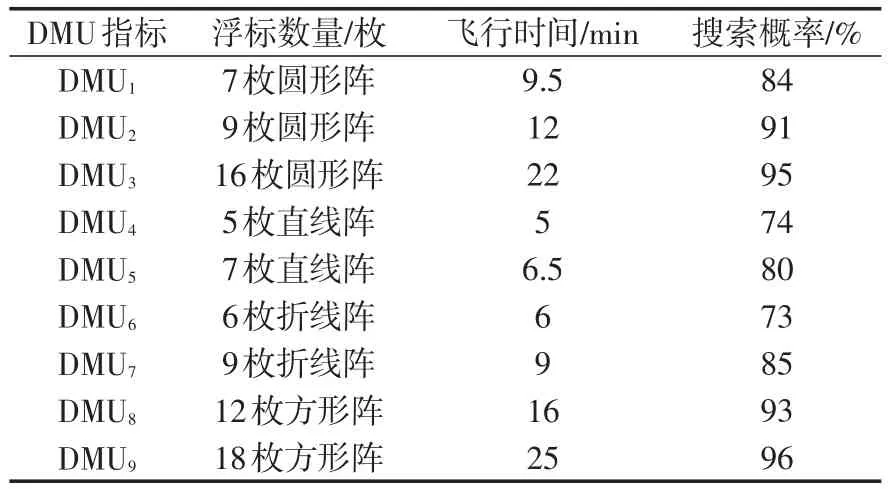
表3 声纳浮标搜索阵决策单元举例Tab.3 Sonar buoy search array decision unit for example
3.2 ANP网络层次分析
ANP分析工具是基于ANP模型自主设计的,支持ANP可视化建模,矩阵建立与计算,专家评判,打分结论。[14]
根据ANP指标体系建立相关模型,如图7所示。本算例中,由模拟专家评判得出9种方案的综合得分,如图8所示。专家评分结果如图9所示,即5枚直线阵的综合得分为78,7枚直线阵的得分为84,6枚折线阵的得分为76,9枚折线阵的得分为83,12枚方形阵的得分为87。
3.3 DEA/ANP声纳浮标搜潜方案评估
DEA方法中,5枚直线阵、7枚直线阵、9枚折线阵为有效方案,预测探潜效率分别为74%、80%、85%,但整个分析过程并未考虑决策者偏好等因素,此结论并不完全符合决策者的意愿。[15]
ANP模型分析反映了浮标搜潜过程中复杂的关系,对模型体系进行了全面完整的直观构建。[16]通过ANP分析,5枚直线阵的综合得分为78、7枚直线阵的综合得分是84,9枚折线阵的综合得分为83。
经过比较DEA与ANP方法的结论,在DEA客观评价后的基础上,通过ANP分析工具对方案进行比较。[17]在DEA筛选和ANP评估后的方案中得出最优的方案为7枚浮标直线阵的布放方法。[18]
4 结论
本文提供了在反潜巡逻机应召搜潜效能评估中,声纳浮标搜潜方案选择的新方法。首先建立决策指标体系,通过对反潜作战搜潜方案两级结构的分析,分别对ANP和DEA的决策指标体系进行构建。建立DEA/ANP评价模型并根据网络层次分析法(ANP)的基本理论对模型进行优化。在声纳浮标搜索阵决策单元评估算例分析中,先运用DEA对方案进行客观性较强的横向评价,得出忽视决策者主观因素的方案结论。利用自主研发的面向领域ANP分析工具进行可视化描述与科学决策,对方案进行主观性较强的纵向比较。结合两次评价结果得到最优的结论。最终的声纳浮标搜索阵方案排除了明显不符合指挥员意愿的类型,并且具有很强的客观性和合理性。
[1]屈也频.反潜巡逻飞机搜潜辅助决策系统建模与仿真研究[D].长沙:国防科学技术大学,2008.QV YEPIN.Researeh on modeling and simulation for the decision support system of search submarine scheme by antisubmarine warfare patrol aircrafts[D].Changsha:National Defense Science and Technology University,2008.(in Chinese)
[2]刘睿,余建星,孙宏才,等.基于ANP的超级决策软件介绍及其应用[J].系统工程理论与实践,2003,3(8):141-143.LIU RUI,YU JIANXING,SUN HONGCAI,et al.Introduction to the ANP super decisions softw are and its application[J].System Engineering Theory and Practice,2003,3(8):141-143.(in Chinese)
[3]李春好,孙永河,段万春.基于DEA理论的ANP/BOCR方案评价值综合集成新方法[J].中国管理科学,2010,18(2):56-61.LI CHUNHAO,SUN YONGHE,DUAN WANCHUN.New ANP metasynthesis approach with respect to BOCR meritsbased on data envelopment analysis[J].China Management Science,2010,18(2):56-61.(in Chinese)
[4]孙明太.航空反潜装备[M].北京:国防工业出版社,2012:116-117.SUN MINGTAI.Aviation antisubmarine equipment[M].Beijing:Defense Industry Press,2012:116-117.(in Chinese)
[5]李美娟,陈国宏.数据包络分析法(DEA)的研究与应用[J].中国工程科学,2003,5(6):88-94.LI MEIJUAN,CHEN GUOHONG.A review on the research and application of DEA[J].China Engineering Science,2003,5(6):88-94.(in Chinese)
[6]聂海波.基于DEA/ANP方法旅(团)社会化保障绿色供应企业选择研究[D].长沙:国防科学技术大学,2009.NIE HAIBO.Research on social guaranteeing green supplying corporation selection for the brigade(corps)based on DEA/ANP[D].Changsha:National Defense Science and Technology University,2009.(in Chinese)
[7] 魏权龄.数据包络分析(DEA)[J].科学通报,2000,45(17):1793-1807.WEI QUANLING.Data envelopment analysis(DEA)[J].Science Bulletin,2000,45(17):1793-1807.(in Chinese)
[8]杨力,董一平,刘程程.基于网络层次分析法的煤矿应急救援能力评价[J].工矿自动化,2015,41(3):114-118.YANG LI,DONG YIPING,LIU CHENGCHENG.Evaluation of mine emergency rescue capability based on network analytic hierarchy process[J].Industrial and Mining Automation,2015,41(3):114-118.(in Chinese)
[9]胡子义,谭水木,彭岩.基于ANP超级决策软件中的智能评估计算与应用[J].计算机工程与设计,2006,27(14):2575-2577.HU ZIYI,TAN SHUIMU,PENG YAN.Computation of intelligent ratings based on ANP in super decision and its application[J].Computer Engineering and Design,2006,27(14):2575-2577.(in Chinese)
[10]黄晗,莫东序,程婉静.基于ANP模型的绿色港口竞争力评价[J].技术经济,2017,36(2):117-122.HUANG HAN,MO DONGXU,CHENG WANJING.Evaluation on competitivess of green PORT based on analytical network process[J].Technical Economy,2017,36(2):117-122.
[11]储敏.层次分析法中判断矩阵的构造问题[D].南京:南京理工大学,2005.CHUN MIN.The structure of judgment matrix in analytic hierarchy process[D].Nanjing:Nanjing University of Technology,2005.(in Chinese)
[12]马立杰.DEA理论及应用研究[D].济南:山东大学,2007.MA LIJIE.DEA theory and application research[D].Jinan:Shandong University,2007.(in Chinese)
[13]MOHAMMAD,MEHDITAVAKOLI,HADISHIROUYEHZAD,et al.Proposing a hybrid method based on DEA and ANP for ranking organizational units and prioritizing human capital management drivers[J].Journal of Modelling in Management,2016,11(1):213-219.
[14]BABAKDANESHVARROUYENDEGH,SERPIL EROL.The DEA-FUZZY ANP department ranking model appliedin iran amirkabir university[J].Acta Polytechnica Hungarica,2010,7(4):103-114.
[15]MANOJ KUMAR,JYOTI RAMAN,PRIYA SINGh.An unified analytical network process(ANP)and data envelopment analysis(DEA)approachfor manufacturing strategy decision[J].International Journal of Strategic Decision Science,2015,6(2):34-45.
[16]李志亮,陈世权,吴今培.基于模糊数变换的DEA模型与应用[J].模糊系统与数学,2004,18(4):64-71.LI ZHILIANG,CHEN SHIQUAN,WU JINPEI.The DEA model and application based on fuzzy number transformation[J].Fuzzy System and Mathematics,2004,18(4):64-71.(in Chinese)
[17]马占新,任慧龙,戴仰山.基于模糊综合评判方法的DEA模型[J].模糊系统与数学,2001,15(3):61-67.MA ZHANXIN,REN HUILONG,DAI YANGSHAN.A DEA model based on fuzzy comprehensive evaluation method[J].Fuzzy System and Mathematics,2001,15(3):61-67.(in Chinese)
[18]MASOUD RABBANI,HELIA YUSEFNEJAD.A novel DEANP method for customer order decoupling point positioning in a supply chain[J].International Journal of Industrial and Systems Engineering,2016,22(4):393-408.
