基于中心抽头变压器的倍频感应加热电源

卢 华胡金刚毕 闯向 勇

（1. 电子科技大学能源科学与工程学院 成都 611731 2. 电子科技大学航空航天学院 成都 611731）

基于中心抽头变压器的倍频感应加热电源

卢 华1胡金刚1毕 闯2向 勇1

（1. 电子科技大学能源科学与工程学院 成都 611731 2. 电子科技大学航空航天学院 成都 611731）

针对高频大功率应用场合，提出了一种基于中心抽头变压器的倍频式感应加热电源。采用结构对称的两个半桥、共用谐振电容、抽头变压器耦合的方式，使得负载工作频率为功率开关管工作频率的两倍，达到倍频的目的。功率开关管具有软开关特性，且导通时间为其开关周期的25%，相对于传统的桥式逆变器来说，明显降低了开关管的功耗。详细分析了8个不同的工作模式及相应的系统参数关系，给出了电路参数的设计方法。最后以IGBT为功率开关管，设计了一台小型样机，通过实验验证了所提出的电源拓扑、理论分析及参数选取方法的正确性。

感应加热 倍频 抽头变压器 半桥

0 引言

感应加热电源因具有功率因数高、电磁干扰小、加热效率高等优势，得到了广泛的研究与应用[1-4]。在工程应用中，感应加热电源输出功率和频率是两项重要指标，在低频大功率场合，如金属熔炼，一般采用晶闸管或绝缘栅双极晶体管（IGBT）[2,3]。由于IGBT的开关损耗以及拖尾电流的限制，其应用一般低于100kHz，对于更高频率的应用场合，则采用金属氧化物半导体场效应晶体管（MOSFET）[5-7]。对于金属淬火、焊接等应用场合，要求高频大功率的电源[3]，虽然MOSFET可以达到高频的要求，但单个MOSFET的功率容量有限。提高MOSFET应用功率的方法是采用多管并联的形式，但该方法不但降低了电源的稳定性，同时提高了成本[6,8]。IGBT易于大功率化，且相比并联MOSFET，具有成本优势[6]。但由于IGBT开关频率的限制，很难实现高频化。

对于IGBT的高频化应用，可采用倍频拓扑，间接拓宽应用频率。文献[6,9]直接并联逆变单元，分时控制各单元，并联的数量即为倍频数。文献[10]提出了基于并联IGBT器件的倍频式电源，通过分时控制各IGBT达到倍频的目的。上述方法的不足之处在于增加了IGBT数量，从而导致成本大幅提升。文献[11]论述了一种倍频式IGBT高频感应加热电源拓扑，该拓扑具有换流和负载两个谐振槽路，电路结构相对复杂，且当两个槽路谐振频率接近时，很难实现负载匹配。

全桥、半桥拓扑及抽头变压器在电源中应用广泛[2-5,12]，本文基于桥式拓扑和中心抽头变压器，提出一种IGBT倍频式感应加热电源拓扑，其负载频率是开关频率的两倍，间接拓宽了IGBT的使用频率，适合高频大功率应用场合。该拓扑在传统的H桥逆变感应加热电源基础上，增加了谐振电容，同时将匹配变压器换成中心抽头变压器。本电源拓扑结构简单，器件应力与半桥相同，且可实现软开关，相对于其他倍频方法，控制简单，无需额外增加IGBT，具有很强的工程应用价值。

1 工作原理

1.1 主拓扑结构

基于中心抽头变压器的倍频IGBT感应加热电源主拓扑如图1所示。

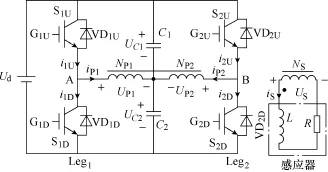
图1 倍频IGBT感应加热电源主拓扑Fig.1 Main topology of frequency doubling IGBT induction heating power supply

图1中，Ud为电源电压，S1U、S1D、S2U、S2D为IGBT；VD1U、VD1D、VD2U、VD2D为反并联二极管；C1、C2为谐振电容；G1U、G1D、G2U、G2D为IGBT门极；NP1(NP2)、NS分别为变压器一次和二次绕组匝数，其中NP1=NP2，匝比n=NP1/NS，变压器极性如图1所示；L、R分别为感应加热线圈带载时的等效电感和等效电阻。拓扑中各节点、支路的信号及参考方向如图1所示。该拓扑可认为是由两个半桥Leg1、Leg2组成，两支桥臂共用谐振电容C1与C2。

1.2 工作状态

理论分析时，忽略IGBT导通时间和压降，变压器全耦合，忽略谐振电容等效串联电阻和死区时间。为了IGBT结电容在导通前释放电荷，通常负载呈弱感性，即谐振电流相位滞后于电压相位。

倍频IGBT感应加热电源主要工作波形如图2所示。图2中，G1U、G1D、G2U、G2D为驱动信号，开关周期为t0～t8，导通占空比均为25%，负载谐振频率为IGBT开关频率的2倍，从而实现倍频的目的。

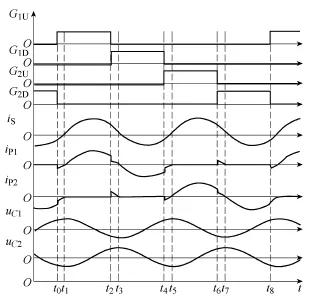
图2 倍频IGBT感应加热电源主要工作波形Fig.2 Key waveforms of frequency doubling IGBT induction heating power supply

稳态工作时，整个开关周期共包含8个工作模式，均满足UC1+UC2=Ud，具体分析如下。

1）模式1[t0,t1]，如图3a所示。在t0时刻，开关管S2D关断、S1U开启，由于电流iS的波形滞后于开关波形，因此在t0～t1时间内，iS、iP1及iP2的方向为参考负方向。此时存在两支电流回路：NP2—VD2U—C1和NP1—VD1U—Ud—C2，iP1通过VD1U续流，iP2通过VD2U续流，并给C1充电；iP1流入电源Ud，C2被反向充电。模式1结束时，iS、iP1及iP2降到0，C1电压上升到最大值，C2电压达到反向最大值，电感L的能量部分反馈回电源。由于节点A、B与直流源Ud等电位，因此S1D、S2D的电压应力为Ud。

零电压导通分析：在t0～t1时间段内，虽然S1U的导通信号已经送达，但是由于IGBT反并联二极管被导通，S1U的端电压为0，电源电压Ud并没有立即施加到S1U两端，故模式1实现了零电压导通（Zero Voltage Switch, ZVS）。

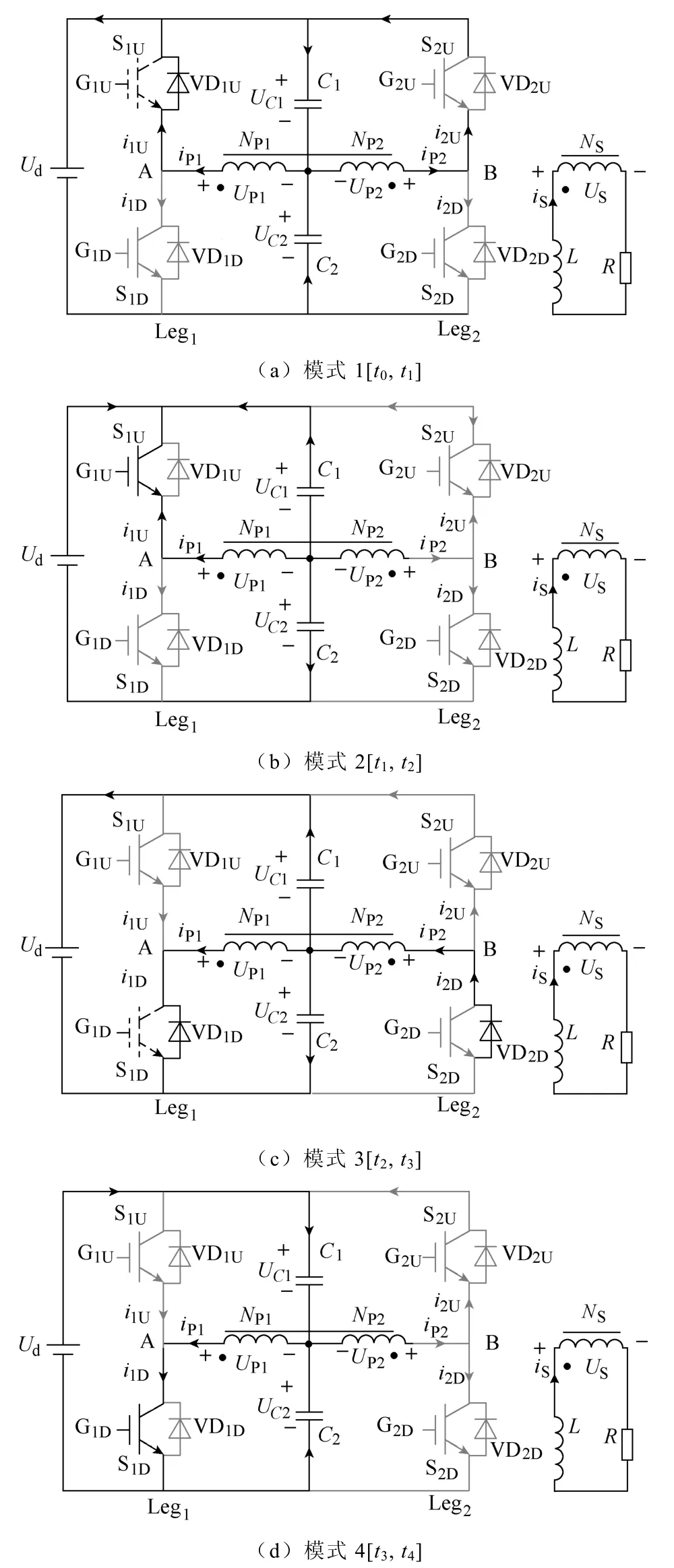
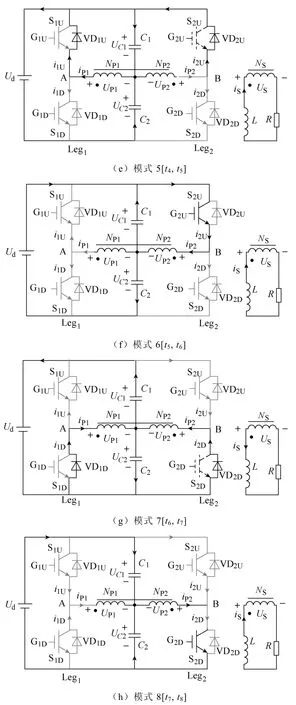
图3 倍频感应加热电源工作模式Fig.3 Operation modes of frequency doubling induction heating power supply

2）模式2[t1,t2]，如图3b所示。在t1时刻，电流iP1和iP2均减小为0，此后由于Leg2的S2U、S2D均处于关断状态，因此iP2保持为0，而iP1将正向增加。L、R通过变压器NP1与C1、C2谐振，此时存在两个谐振回路，分别为NP1—C2—Ud—S1U和NP1—C1—S1U。模式2阶段，谐振电流均为正参考方向。根据中心抽头变压器的工作原理，可知UP1=UP2，因此A、B点等电位，故S2U的电压应力为0，S1D与S2D的电压应力均为Ud。

3）模式3[t2,t3]，如图3c所示。在t2时刻，S1U关断、S1D开通，由于iS尚未减小到0，因此iP1也未减小到0，iP1经过VD1D续流。根据中心抽头式变压器的原理可知，节点A和B的电位相等，VD1D被导通的同时，反并联二极管VD2D也被导通，iS的续流一部分通过iP2完成。因此，在t2时刻，iP1突降，同时iP2突增。模式3期间，系统同样存在两个谐振回路：Ud—VD1D—NP1—C1和VD2D—NP2—C2。谐振过程中，C1被反向充电到最大值，C2被正向充电到最大值。根据节点A、B的电位可知，开关管S1U和S2U电压应力均为Ud。

同理，模式1、模式3实现了S1D的零电压导通。

4）模式4[t3,t4]，如图3d所示。在t3时刻，iS减小到0，iP1和iP2也减小为0。S1D处于导通状态，故iP1反向增加，S2D处于截止状态，故iP2保持为0。L、R通过变压器NP1与C1、C2谐振，此时两个谐振回路分别为Ud—C1—NP1—S1D和NP1—C2—S1U。模式4期间，谐振电流均为参考负方向。A、B点的电位相等，故S1U与S2U的电压应力均为Ud，S2D的应力为0。

5）模式5[t4,t5]，如图3e所示。在t4时刻，S1D关断、S2U开启。模式5与模式1基本相同。模式5各参数关系如式（5）所示。同理，S2U零电压导通。

6）模式6[t5,t6]，如图3f所示。S1U处于关断状态，故iP1保持为0。模式6与模式2近似，不同的是：由于S2U处于导通状态，谐振回路开始轮转到Leg2。

7）模式7[t6,t7]，如图3g所示。在t6时刻，开关管S2U关断、S2D开通。工作模式7与工作模式3基本相同。

同理，模式1、模式7实现了S2D的零电压导通。

8）模式8[t7,t8]，如图3h所示。模式8与模式4近似。

模式8结束后，S2D关断，S1U开启，系统进入模式1，开始下一周期的循环运行。

2 电路参数设计

理论计算时，需要作如下假设：①IGBT为理想开关，忽略寄生电容和开通时间；②谐振电容无寄生电阻，抽头变压器为理想变压器；③负载品质因数Q足够大，从而保证谐振电流（iP1、iP2）按正弦规律变化。

根据第1节中的工作模式分析可知，若开关频率等于谐振频率的1/2，则稳定工作状态只包含模式2、4、6、8。一个开关周期内，系统的Leg1和Leg2各完成一次谐振，且完全对称，因此在进行等效电路分析时，仅考虑Leg1的谐振周期即可。根据变压器的阻抗变换作用，将二次绕组NS串接的电感L和电阻R等效到一次绕组NP1，电源等效电路如图4所示。

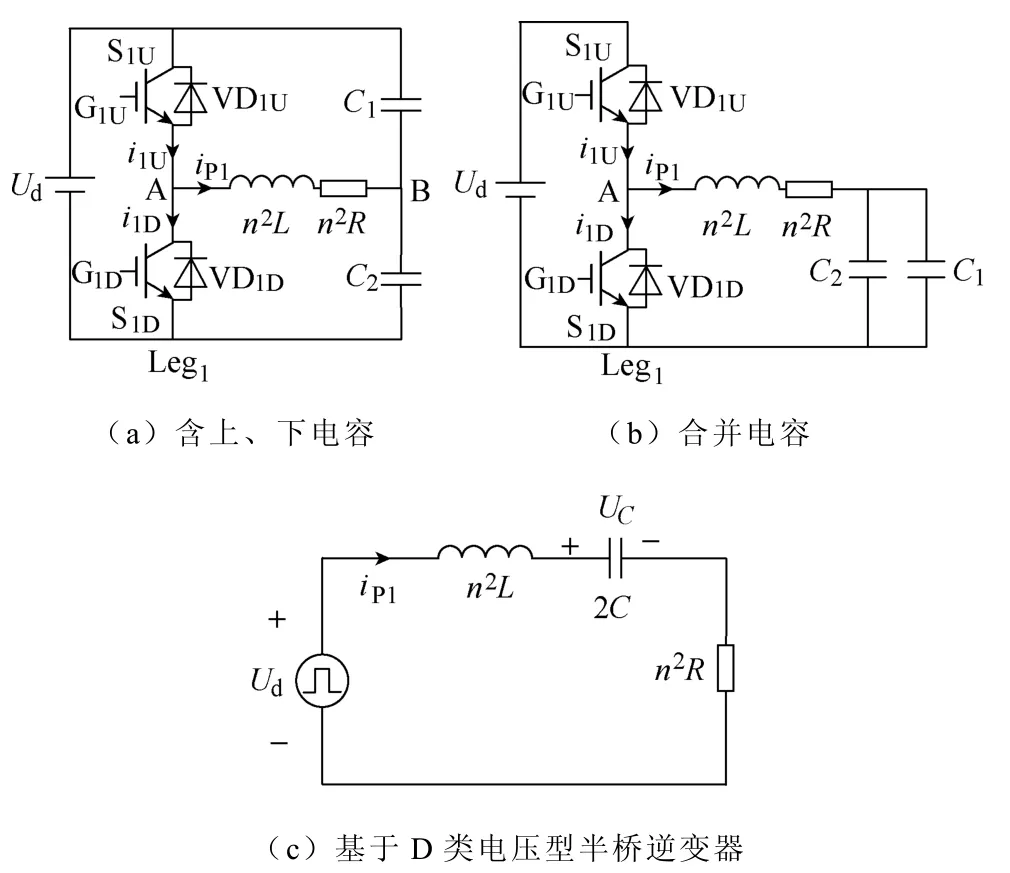
图4 电源等效电路Fig.4 Equivalent circuits of power supply

图4中，n为变压器匝比（n=NP1/NS），图4c中C=C1=C2。根据文献[13]，谐振角频率ω0和负载品质因数Q分别为

在一定的工况环境下，根据负载的要求，已知最大输出功率P、负载角频率ω、负载线圈的等效电感L以及等效负载R。工程中一般要求谐振槽路固有角频率ω0与负载要求的角频率接近，即ω0≈ω，根据式（4）可知，cosψ≈1。首先，根据最大输出功率P、工况中提供的最大电源Ud以及式（10），计算中心抽头负载匹配变压器匝比n；然后，由已知的负载角频率ω、负载等效电感L以及Q值要求，结合式（1）和式（2）计算电容C；最后，根据式（9）和式（11）选取满足额定电压、额定电流要求的谐振电容。

3 实验

设计样机输出至负载的功率P=500W，测得线圈50kHz下的等效电感为1.63μH，等效电阻0.29Ω，中心抽头变压器匝比n=6。高频感应加热电源不同于其他选频电路，特别是对调频调功和脉宽调功的电源而言，Q值较小（Q≤3）[5,14]，本实验中，设Q=1.5。根据式（10），在cosψ≈1时计算得到电源Ud= 161.5V，考虑电路损耗及功率因数，实验输入电源Ud=180V。根据式（1）和式（2）得到谐振电容C=0.117μF，实际选择0.1μF。因此，电路的理论谐振频率f0=46.92kHz。样机实验波形如图5所示。

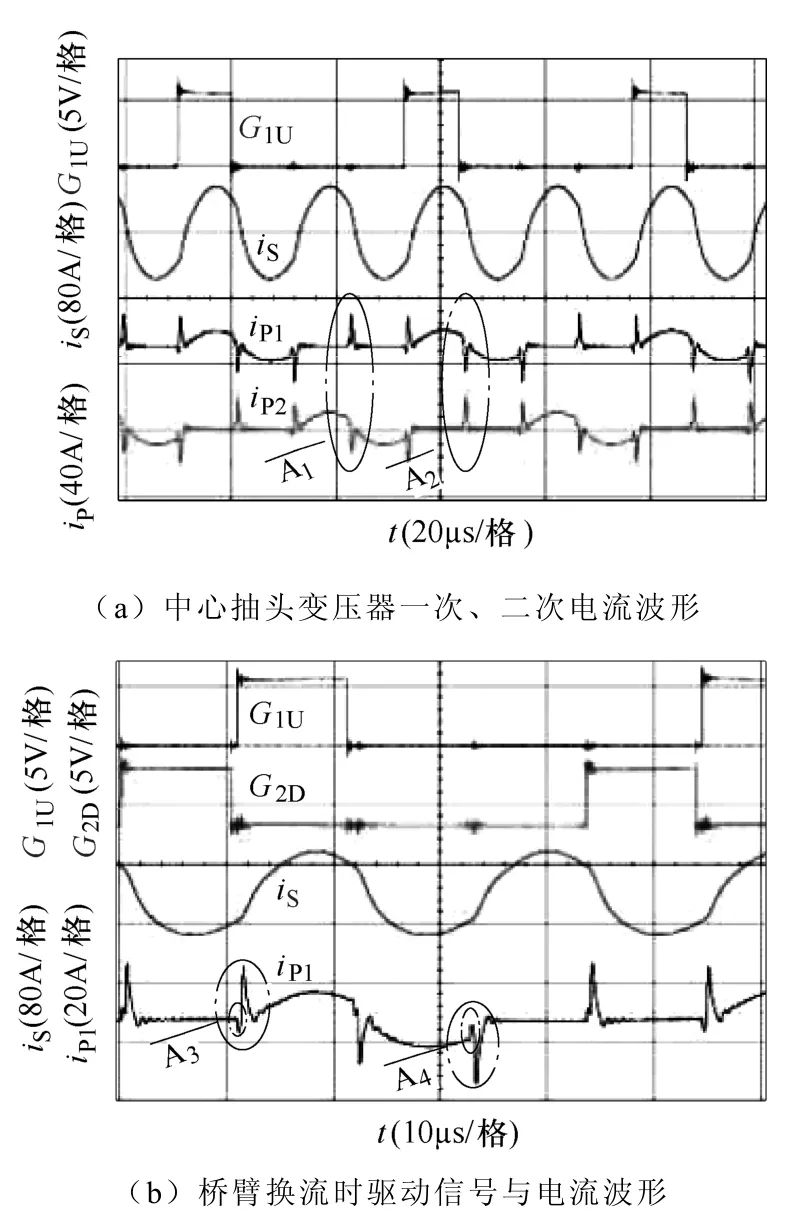
图5 样机实验波形Fig.5 Experimental waveforms of prototype

图5a中G1U为IGBT开关管S1U的驱动信号，iP1、iP2、iS分别为中心抽头变压器的两个一次电流和二次电流；图5b中G2D为IGBT开关管S2D的驱动信号。从图5a中的G1U和iS可以看出，电流谐振频率为IGBT驱动信号频率的2倍，实现了倍频功能。图5中驱动信号频率（即IGBT开关频率）fs=22.97kHz，经二倍频后，负载谐振电流频率为45.94kHz，低于计算值f0（46.92kHz），原因在于计算时未将IGBT寄生电容和吸收电容考虑在内，这些电容的存在，使得实际谐振频率低于计算值。

图5a椭圆框A1、A2所示的波形与工作模式7和模式3理论分析波形趋势一致，该波形是桥臂上下IGBT工作交换时产生的，实现了IGBT零电压开通。图5b中，A3、A4框所示的波形为桥臂Leg1与Leg2交替时产生的波形，分别对应模式1和模式5的波形，可以看出此处与理论分析波形不尽相同。从A3框可以看出，在S2D的关断信号G2D开始时，变压器一次电流iP1从0下降为负值，然后突增产生电流尖峰，当尖峰下降到相应的正弦波形幅度时，才遵循工作模式2所示的正弦变化规律。

电流尖峰分析：如图5b所示，在G2D关断的瞬间，由于实验中死区时间的存在，G1U并没有立即导通，此时开关管S1D、S2D吸收电容被充电。由于死区时间较短，吸收电容偏大，在死区时间结束时，iP1、iP2尚未衰减至零，S1D、S2D的吸收电容端电压并没有被充至Ud，但此刻G1U已开启，节点A、B的电位迅速降至Ud。于是线圈NP2以较大的电流给S2D的吸收电容充电，直到充至Ud。由于磁耦合作用，此时iP2由电源通过线圈NP1提供，因此iP1形成正向尖峰，如图5b中A3框所示，同理可分析A4框的负向尖峰。

总体来说，虽然A3、A4框的波形与模式1和模式5的理论分析波形不完全一致，但A3、A4框内的波形趋势与模式1和模式5的理论分析一致，说明了理论分析的正确性。

4 结论

本文提出了一种基于中心抽头变压器的倍频式IGBT感应加热电源，通过仿真和理论分析，揭示了该倍频电源的工作原理，分析了IGBT器件的电压应力、软开关工作特性，并给出了电路中各主要器件参数的设计与计算方法。最后根据该方法设计了一台小型样机，通过实验证明了该电路的二倍频效果，验证了理论分析以及电路参数设计方法的正确性，对该电源的工程应用具有一定的指导意义。

[1] 王启涵, 姚缨英, 陈卫宝. 电磁感应加热中加热物体位置的选择[J]. 电工技术学报, 2011, 26(6): 160-165. Wang Qihan, Yao Yingying, Chen Weibao. Selection of heating object’s position in electromagnetic induction heating[J]. Transactions of China Electrotechnical Society, 2011, 26(6): 160-165.

[2] Bayindir N S, Kükrer O, Yakup M. DSP-based PLL controlled 50-100kHz 20kW high frequency induction heating system for surface hardening and welding applications[J]. IEE Proceedings-Electric Power Applications, 2003, 150(3): 365-371.

[3] Zok E, Schibisch D M. Energy efficient power supply for induction hardening and heating processes[J]. Induction Technology Reports, 2013(1): 67-74.

[4] 李宏, 贺昱曜, 王崇武. 一种全桥负载串联谐振逆变器谐振频率跟踪和输出功率控制方法[J]. 电工技术学报, 2010, 25(7): 93-99. Li Hong, He Yuyao, Wang Chongwu. A new method of frequency tracking and output power control for full bridge series load resonant inverter[J]. Transactions of China Electrotechnical Society, 2010, 25(7): 93-99.

[5] Lucia O, Burdio J M, Millan I, et al. Efficiencyoriented design of ZVS half-bridge series resonant inverter with variable frequency duty cycle control[J]. IEEE Transactions on Power Electronics, 2010, 25(7): 1671-1674.

[6] Zied H A, Mutschler P, Bachmann G. A modular IGBT converter system for high frequency induction heating applications[C]//23rd International Conference and Exhibition on Power Electronics, Intelligent Motion, Power Quality, Europe, 2002.

[7] 李时峰, 吕默影, 陈辉明. 一种新型超高频感应加热混合全桥逆变器[J]. 电工技术学报, 2013, 28(3): 215-221. Li Shifeng, Lü Moying, Chen Huiming. A novel hybrid full-bridge inverter for ultra-high frequency induction heating applications[J]. Transactions of China Electrotechnical Society, 2013, 28(3): 215-221.

[8] Mollov S V, Theodoridis M, Forsyth A J. High frequency voltage-fed inverter with phase-shift control for induction heating[J]. IEE Proceedings-Electric Power Applications, 2004, 151(1): 12-18.

[9] Kleveland F, Undeland T M, Langelid J K. Increase of output power from IGBTs in high power high frequency resonant load inverters[C]//Industry Applications Conference Record of the 2000 IEEE, Rome, 2000: 2909-2914.

[10] 熊一频, 沈锦飞, 初中原. 基于IGBT倍频式180kHz感应加热电源研究[J]. 电力电子技术, 2008, 42(11): 58-59. Xiong Yipin, Shen Jinfei, Chu Zhongyuan. Research on an 180kHz double frequency induction heater based on IGBT power electronics[J]. Power Elec-tronics, 2008, 42(11): 58-59.

[11] Zhu Z Q, Wu L J, Xia Z P. An accurate subdomain model for magnetic field computation in slotted surface-mounted permanent-magnet machines[J]. IEEE Transactions on Magnetics, 2010, 46(4): 1100-1115.

[12] 吴靖, 王正仕, 赵荣祥, 等. 倍频式高频感应力加热电源工作模式[J]. 电工技术学报, 2007, 22(2): 153-158. Wu Jing, Wang Zhengshi, Zhao Rongxiang, et al. Working method of double-frequency mode high frequency induction-heating power supply[J]. Transactions of China Electrotechnical Society, 2007, 22(2): 153-158.

[13] Kazimierczuk M K, Czarkowski D. Resonant power converters[M]. New Jersey: John Wiley & Sons, 2012.

[14] 李定宣, 丁曾敏. 现代感应加热电源工程设计与应用[M]. 北京: 中国电力出版社, 2010.

Frequency Doubling Power Supply for Induction Heating Based on Center-Tapped Transformer

Lu Hua1Hu Jingang1Bi Chuang2Xiang Yong1
（1. School of Energy Science and Engineering University of Electronic Science and Technology Chengdu 611731 China 2. School of Aeronautics and Astronautics University of Electronic Science and Technology of China Chengdu 611731 China）

A novel multiple-frequency power supply is proposed for high frequency high power induction heating appliances based on center-tapped transformer. Its output frequency is as twice as the device frequency, by using two symmetrical half bridges, sharing two equal resonant capacitances and coupling with center-tapped transformer. Each power switch has zero voltage switch (ZVS) soft switching characteristic, and its conduction time is only a quarter of switching cycle. Thus the power consumption of the switches decrease significantly compared with the traditional inverter. The eight operation modes are analyzed, and the design methods of circuit parameters are also present. Taken IGBT as power switches, a prototype is designed to verify the power supply topology, the theoretical analysis and the circuit parameter selection method.

Induction heating, frequency doubling, center-tapped transformer, half-bridge

TG155.21

卢 华 男，1989年生，硕士，研究方向为高频感应加热电源。E-mail: 2008luhua@uestc.org

毕 闯 男，1983年生，博士，副教授，研究方向为电力电子技术及电磁兼容。

E-mail: chuang.bi@uestc.edu.cn（通信作者）

四川省国际合作计划项目（2016HH0009）和四川省科技支撑计划项目（2016GZ0335）资助。

2014-09-03 改稿日期 2015-01-20