老化实验条件下的IGBT寿命预测模型

赖 伟陈民铀冉 立王学梅徐盛友

（1. 输配电装备及系统安全与新技术国家重点实验室（重庆大学） 重庆 400044 2. 华南理工大学电力学院 广州 510640）

老化实验条件下的IGBT寿命预测模型

赖 伟1陈民铀1冉 立1王学梅2徐盛友1

（1. 输配电装备及系统安全与新技术国家重点实验室（重庆大学） 重庆 400044 2. 华南理工大学电力学院 广州 510640）

以器件功率循环为基础，在疲劳损伤理论基础上建立功率器件寿命模型，以提高变流器的运行可靠性，为功率变流器的检修维护提供理论基础。给出了器件寿命预测模型的使用价值和意义，通过分析功率器件失效机理，设计了功率循环实验平台和老化实验方案，阐述了老化实验原理并给出了老化参数提取方法。利用Weibull分布建立了器件的一维寿命模型并分析了该模型的优缺点，提出了改进的器件三维寿命模型，通过对比、分析证明了该模型的准确性，得到的Arrhenius广延指数模型更能体现器件寿命分布。

寿命模型 功率循环 Weibull分布 Arrhenius广延指数模型 IGBT

0 引言

随着我国新能源发电规模、容量的不断增大，电力系统必须面对越来越艰巨的维护和检修任务。本文针对新能源发电系统中普遍使用的电力电子变流器进行研究。一方面，新能源发电系统受气候条件影响较大，具有较大的随机波动性，变流器长期处于交变的疲劳载荷下，加速了材料和内部封装结构的老化，导致故障率增高。另一方面，这些发电系统的单机容量相对较小、机组布置分散且偏远，进场维修不便。因此，降低故障率和提高维修效率尤其重要。有关分析显示，海上风电机组的故障率必须限制在1次/（年·台）以下，近海风场才具有经济上的可行性。目前，陆上变速风机的故障率大约在2次/（年·台），其中，与机-电能量转换系统，特别是变流器及控制系统有关的故障占主要部分。因此，提高变流器可靠性显得尤为迫切和重要。

变流器是将可再生能源电能并入电网的纽带，既能控制对电网输送发电的有功分量，又能连接、调节电网端无功分量，起到无功补偿的作用。IGBT模块作为功率变流器的主要部件，受负载、机械振动、环境条件、加载在电力电子系统上的应力[1]等因素影响。图1为电力系统失效分布，由图可知，研究温度对半导体器件可靠性的影响是提高和监测可再生能源发电系统可靠性的有效途径。目前各大风电企业如Vestas、Siemens、GE以及输电装备企业如ABB、Alstom都对变流器特别是用于海上变流器的可靠性予以高度重视。例如，Siemens风机变流器的模块化设计，近期致力于研究实时检测器件的老化进程，以制定更加合理有效的检修计划。文献[2-4]定量地分析了不同结温温差ΔTj和焊接层材料对器件寿命的影响。文献[5-8]通过模拟分析IGBT内部热应力分布，研究了功率循环过程中功率器件焊接层的失效机理和焊接层中空洞含有率对器件性能的影响。文献[9]给出了Coffin-Manson寿命预测模型，但是该模型参数从小样本实验得到，缺乏一般性且并未考虑平均结温Tjm的作用。文献[10-12]提出了IGBT器件的寿命同时受ΔTj和Tjm两个参数影响。因此，Arrhenuis提出了基于Coffin-Manson的改进模型，该模型同时考虑了结温均值和结温幅值对寿命的影响，在LESIT中只给出了特定Tjm下的模型[9]。当前，国内外正试图寻找各种方法，对变流器功率器件的老化应力进行控制和管理，以应对运行工况的不确定性，提升整个产品周期内的可靠性水平。然而所有这些工作，都在很大程度上依赖于较为准确的器件寿命模型，本文采用加速老化寿命实验方法，从热应力作用的实际机理出发，建立了更贴近实际的应力寿命模型。

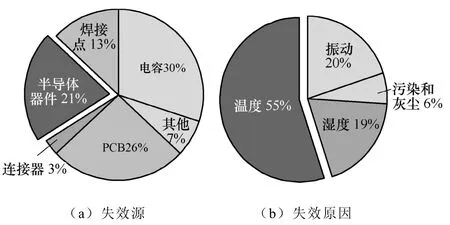
图1 电力系统失效分布Fig.1 Failure distribution of power electronic system

1 IGBT失效原因

IGBT模块由多层组成，每层材料的膨胀系数（Coefficient of Thermal Expansion, CTE）不同，见表1，层间差值ΔCTE如图2所示。IGBT模块工作时，热源主要是Si芯片的结温Tj，从模块SKM50GB123D的数据表可得该模块正常工作的Tj范围为-40℃～150℃。而与芯片相连接的铝引线、焊接层的CTE差异较大。Tj=120℃时，铝引线和Si芯片的热膨胀差值是2.28×10-3/℃，而芯片与焊接层的热膨胀差值是3×10-3/℃，较大的差值是造成IGBT模块失效的主要原因。模块长期工作在热循环冲击下导致材料疲劳和老化，使得模块先发生焊接层失效，然后引线发生失效[13]。所以焊接层失效过程能反应模块工作状态，而焊接层失效过程主要引起热阻的变化，故监测热阻是实现模块状态监测的重要手段。

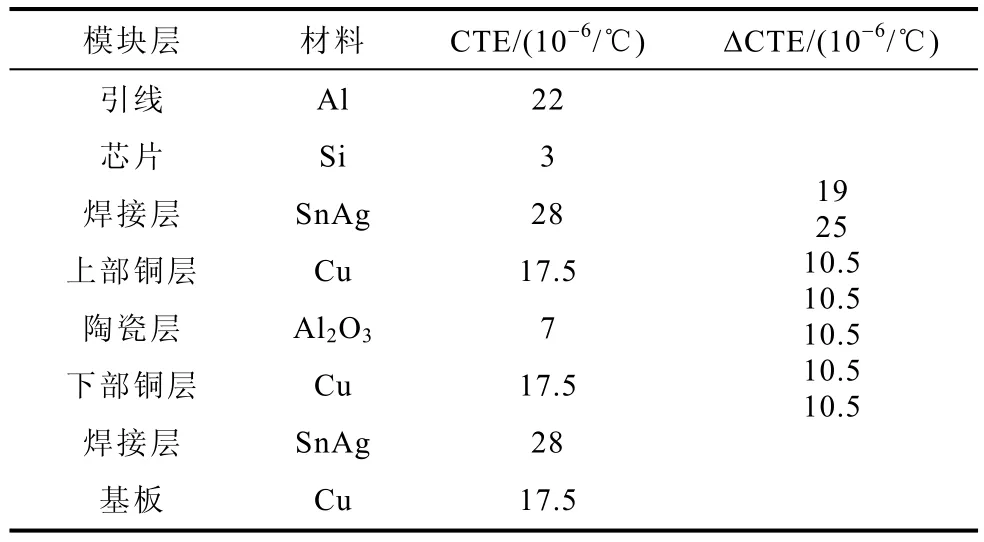
表1 IGBT模块各层材料及其CTETab.1 Materials and their CTE for each layer of IGBT module

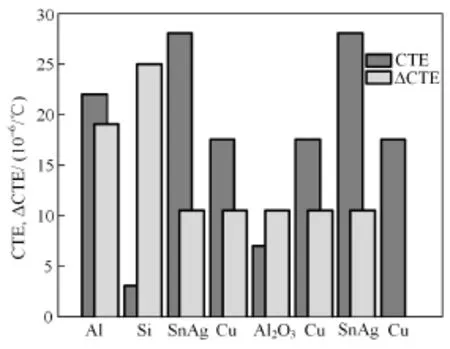
图2 IGBT每层CTE及层间ΔCTEFig.2 CTE and ΔCTE distribution of the IGBT

在老化实验中，通过监测热阻的变化判断焊接层是否失效。热阻由热传导方程计算[14-16]，即

式中，Rth为热阻；Ploss为功耗；Tc为壳温。

2 老化实验原理

本文通过对11对半桥IGBT模块串联，进行功率循环老化实验，获取模块焊接层热阻（焊接层失效）和模块饱和压降Vce变化（引线失效）趋势。在实验中选取壳温Tc作为加热、冷却过程结束的标志量，因为Tc可以在不破坏模块封装的前提下，通过温度传感器直接测量。焊接层失效主要引起模块热阻的变化，而铝引线脱落则是改变Vce。传统模块失效标准是导通电压增加5%，热阻增加20%[17]。文中考虑实验误差和模块实际失效时参数情况，定义导通电压增加10%，热阻增加50%为模块失效标准。

采用恒定应力加速寿命实验[18,19]（功率循环实验），其实验原理如图3所示，该电路由被测IGBT、控制开关和保护电感等组成。当控制开关给导通信号时，测试模块通大电流即模块功耗较大，结温迅速上升；结温上升至设定值时切除外部大电流冲击，通100mA电流（小电流下模块无自热）测Vce值，同时冷却系统工作，使模块温度下降至设定最小值。该过程为恒定应力加速寿命实验周期。利用100mA下结温与Vce的线性关系计算结温[17]，通过式（1）提取热阻值。本文使用NI USB-6225 OEM数据采集卡，由于功率模块的热惯性时间常数范围为100～200ms，而采集卡的最大采样率约为10.4kHz，即采样周期约0.104ms，因此，保证了获取结点温度值的准确性。

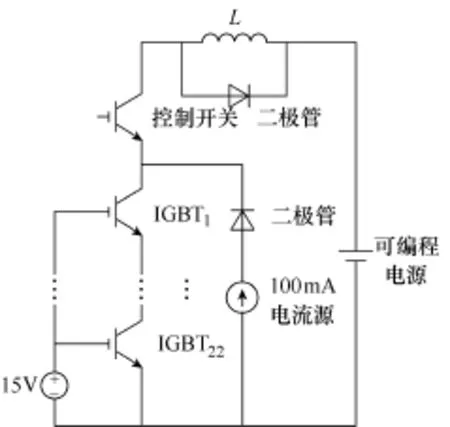
图3 老化实验主电路Fig.3 Main circuit of the aging test

实验中为了减少功率循环的周期，采用液冷方式。液冷系统主要由冷却箱、水泵、控制阀和水冷散热器组成，如图4所示。当模块通额定电流自热时，冷却箱不给散热器提供冷却液，一旦模块加热至设定值时，则打开控制阀给散热器通冷却液，使模块温度迅速下降。

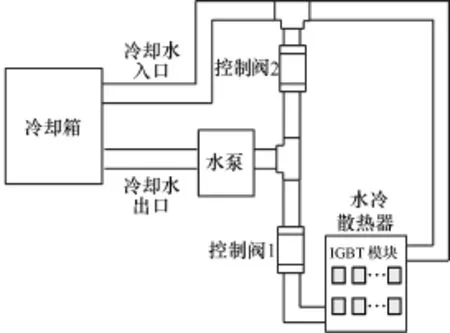
图4 水冷系统Fig.4 Water cooling system

在功率循环实验中，不考虑开关频率、负载情况对器件的影响，假设Si芯片本身不存在老化，即可获得正确的热阻值，确保了该实验的有效性。老化实验平台主要由PC、LabView软件、数据采集卡、冷却装置、数据采集电路、被测和控制IGBT等组成，其结构、实物分别如图5和图6所示。文中主要测试SEMIKRON公司的SKM50GB123D模块。模块寿命主要受结点温度幅值、均值、温度循环频率等影响，在风力发电中变流器受风速影响导致结温差变化，文中主要研究ΔTj对器件的影响，即保证下限值一定，观察不同上限值对器件寿命的影响。设计的实验方案见表2，在该方案中Tc_min、Tc_max1和Tc_max2分别取30℃、120℃和80℃，根据式（1）和模块参数表可以得到结温最大值分别是150℃和110℃进行实验。模块正常失效的过程是焊接层失效到一定程度时，铝引线开始失效。铝引线开始失效至引线完全脱落时间较短，文中不考虑该过程，即提取热阻增加50%的周期数且满足以下条件时的失效参数，其流程如图7所示。

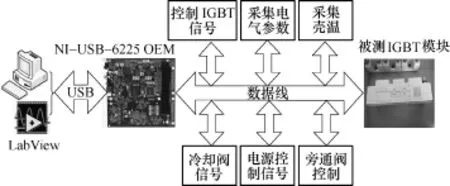
图5 老化实验结构Fig.5 Aging test structure

图6 老化实验平台Fig.6 Aging test platform

表2 老化实验方案Tab.2 Aging test plan (单位：℃)

（1）相邻失效的循环周期数差值应小于100。

（2）失效周期数对应的热阻值与其前后的热阻值差值应小于0.1。

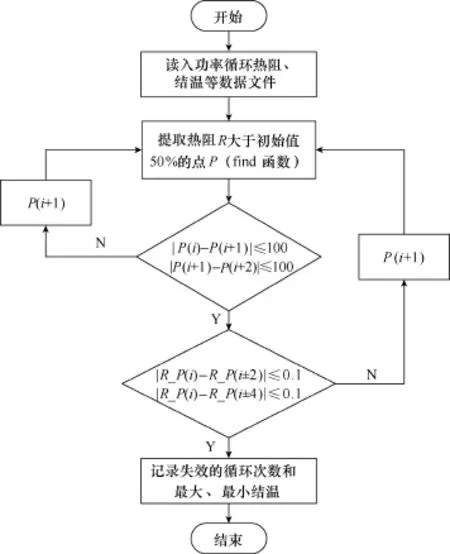
图7 失效参数提取流程Fig.7 Flow chart of extracting failure parameters

3 寿命预测模型

3.1 Coffin-Manson模型

Coffin-Manson模型广泛应用于受交变应力材料寿命估计中，在IGBT模块结构中各层之间不同的热膨胀系数，使得IGBT在不同工作状态下受热应力作用，故可建立Coffin-Manson器件寿命模型[20]为

式中，Nf为失效的循环次数；A1、α1为模型参数。

在器件可靠性统计分析中，通常使用Weibull分布。本文通过Weibull分布来获取IGBT器件寿命模型参数。首先利用老化实验获取IGBT失效数据，并采用概率值计算其分布参数，以建立IGBT器件寿命模型。在热应力下器件寿命服从Weibull分布，其概率密度函数和分布函数分别为

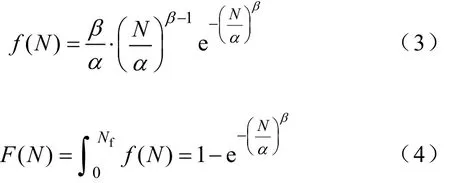
式中，α、β为Weibull分布参数；N为老化循环次数；Nf为器件失效时的循环次数。由式（4）可得

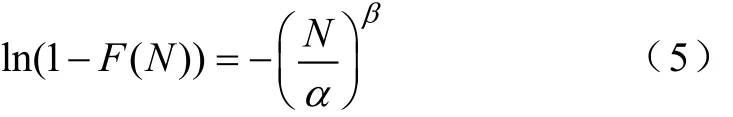
将式（5）进行变形得

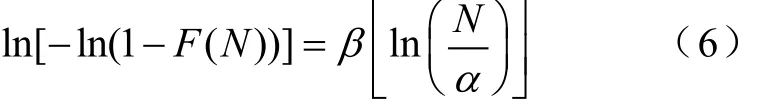
无偏估计F值的计算式为

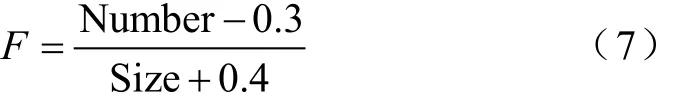
式中，Number为被测IGBT模块编号；Size为被测IGBT模块总数。

在建立器件寿命模型中，分别将测试1和测试2提取的失效参数，按照温度差升序的方式进行排列，利用式（7）计算F值，并利用Matlab以式（5）的形式进行函数拟合，得到的拟合结果如图8所示，参数值α11、β11、α22和β22分别为

根据上述得到的参数值，可以得到实验数据服从Weibull分布，其概率密度函数如图9所示。将F(N)=0.632代入式（6），式（6）左边约等于0，即当概率为63.2%时的循环次数为器件失效的Nf。将α11、β11、α22和β22代入式（4），并取F(N)=0.632得Nf1=13 095、Nf2=65 952。取测试1、2结温差的平均值ΔTj1、ΔTj2分别是125.356 6℃、72.382 2℃，代入Coffin-Manson模型求解方程，得模型参数A1、α1分别为19 226 572 008.39、-2.938 578 46。分别取F(N)=0.40、0.80进行对比可知，F(N)=0.632时误差更小，如图10所示。由图10可知，所建立的寿命模型具有很好的精度，但是该模型只能反应ΔTj与器件寿命的关系，未考虑器件其他工作条件的影响。文献[9,21]提出IGBT寿命模型受多因素影响，并给出了其改进模型，文中寿命模型主要考虑了平均结温的影响。

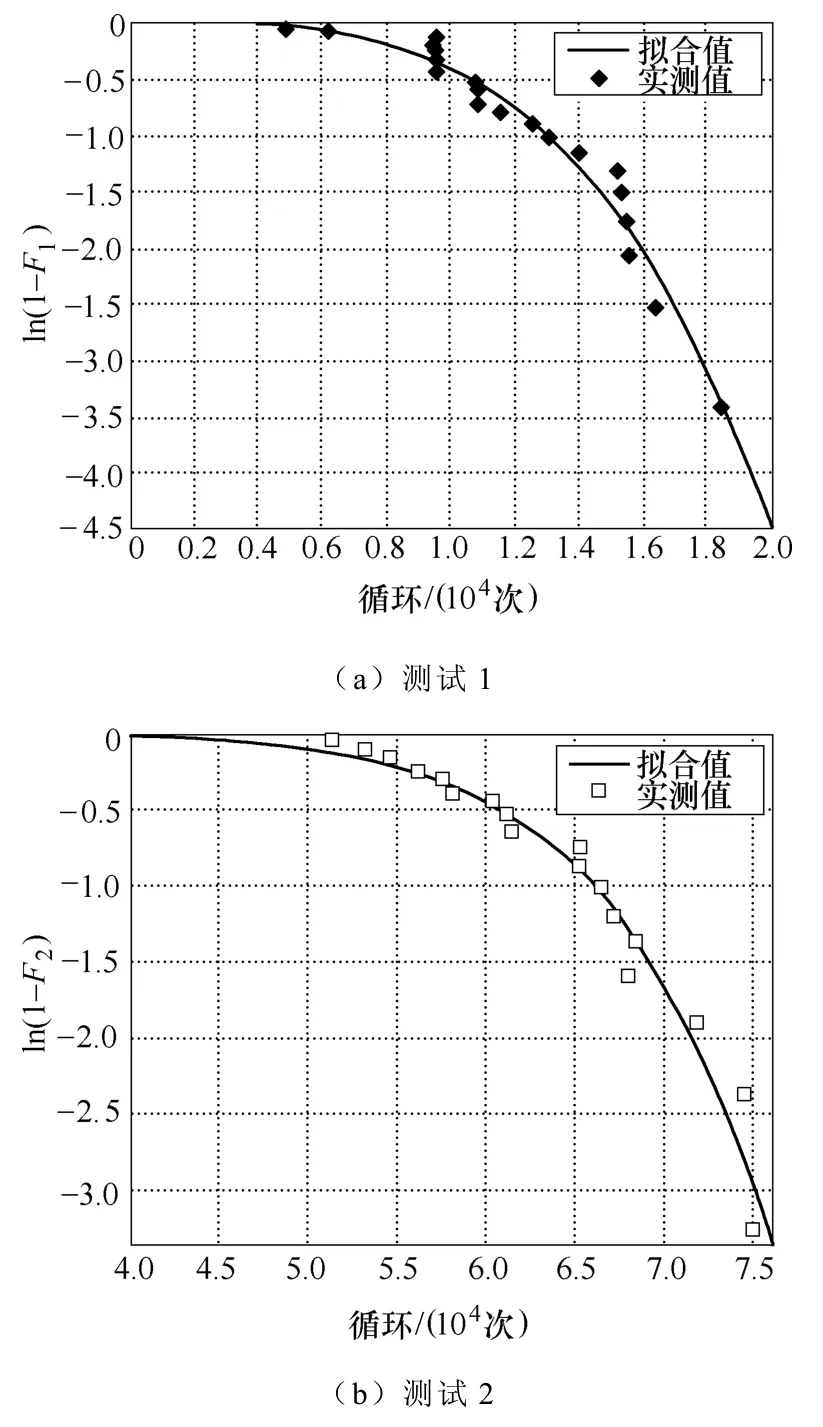
图8 函数拟合结果Fig.8 Result of function fitting

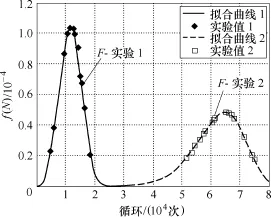
图9 Weibull 概率密度函数Fig.9 Weibull probability density function

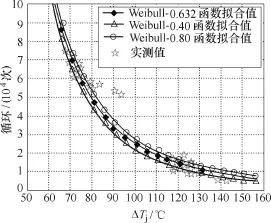
图10 Coffin-Manson模型对比Fig.10 Coffin-Manson model comparison

3.2 Coffin-Manson-Arrhenius模型

根据Arrenius定理可知，温度升高时，热激发过程加强[19]。模块失效主要是由硅层与铜层不同膨胀系数导致器件温度上升，使得材料受热应力发生应变，产生裂缝，最后断裂。该过程温度会变得更高，因Arrenius定理可知该过程构成正反馈。所以本文以失效机理为基础，主要考虑结温差和温度循环平均值对器件寿命的影响，未考虑开关频率、占空比和负载电压、电流等情况。在上述Coffin-Manson模型中，只能给出ΔTj与器件寿命的关系，并未考虑平均结温对器件寿命影响，所以研究学者结合Arrenius定理提出了Coffin-Manson-Arrhenius寿命模型，即

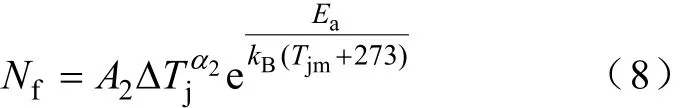
式中，A2、α2为模型参数；Ea为与材料相关的激活能，Ea=9.89×10-20J；kB为玻耳兹曼常数，kB=1.38× 10-23J/K。

在LESIT项目中也给出了该模型，但只给出特定Tjm下的模型参数，本文通过老化实验数据建立适合全段Tjm的Coffin-Manson-Arrhenius模型[20]，并采用麦夸特法[22]对模型参数进行优化拟合，得到参数A2= 0.000 182 017 126 150 9，α2= -0.343 792 946 732 986。

通过相关系数来证明模型结果和实验值的相关性，相关系数计算式为

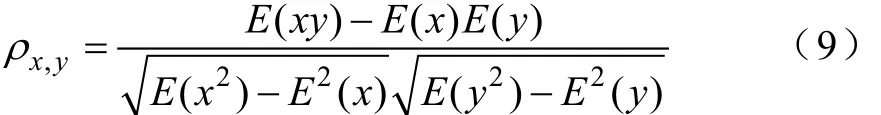
式中，x、y为两个变量；E(x)为变量x的期望。

根据式（9）可得相关系数ρ1=0.942 8，即可用Coffin-Manson-Arrhenius模型表征器件寿命。当ΔTj=110℃、Tjm=80℃时，Nf1=23 737；当ΔTj=110℃、Tjm=90℃时，Nf2=14 930；当ΔTj=120℃、Tjm=80℃时，Nf3=23 037。通过对比可知，当Tjm增加10℃时，失效周期数下降10 169次；而当ΔTj下降10℃时，失效周期仅下降700次。所以，Tjm对器件寿命的影响比ΔTj大。图11为Coffin-Manson-Arrhenius模型结果。由图11可知，ΔTj对器件寿命影响较小，Tjm的影响远大于ΔTj，与实验不符合。这是因为模块失效主要由于IGBT层与层之间的热膨胀系数不同，在功率循环中产生交变热应力作用，导致焊接层变形蠕变，一旦焊接层产生裂缝，受应力集中的作用，焊接层将进一步加速失效或分层。该变形蠕变主要与结温差成正比，即ΔTj是影响器件寿命的主要因素，所以本文提出了降低Tjm影响效果的寿命模型。

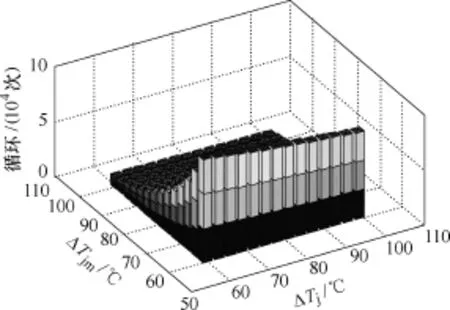
图11 Coffin-Manson-Arrhenius模型结果Fig.11 Results of the Coffin-Manson-Arrhenius model

3.3 Coffin-Manson-Arrhenius广延指数模型

Coffin-Manson-Arrhenius广延指数介于指数分布和幂律分布之间，β3参数能够使模型和数据更好地匹配，降低Tjm的作用强度，所以将器件寿命模型用广延指数进行修正，其计算式为

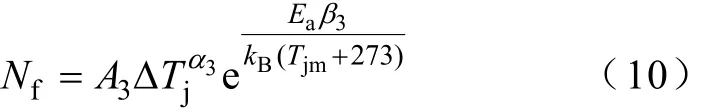
式中，β3取值范围为0～1。采用麦夸特法[15]对模型参数优化拟合，得到A3=684 258.307 264 17，α3= -2.238 566 394 623 18，β3=0.65，其相关系数ρ2= 0.970 2。

当ΔTj=110℃、Tjm=80℃时，Nf1=21843；当ΔTj=110℃、Tjm=90℃时，Nf2=19 231；当ΔTj=120℃、Tjm=80℃时，Nf3=17 977。通过对比可知，当Tjm增加10℃时，失效周期数下降2 612次，而当ΔTj下降10℃时，失效周期仅下降了3 866次。所以，Tjm对器件寿命影响比ΔTj小，符合模块实际失效机理[23,24]。模块结温越高且在相同ΔTj下产生的热应力越大，模块越容易失效。所以，ΔTj是使模块失效的主要因素，Tjm与器件寿命同样成反比关系。

模型结果如图12所示，从图12a中可知，器件寿命在ΔTj方向下降率大于Tjm方向，所以基于广延指数的寿命模型更能体现结温差对器件寿命的影响，符合上述模块实际失效机理。通过对比两个模型的相关系数可知，广延指数模型的相关性更好（ρ2＞ρ1），即广延指数模型更符合器件寿命在不同应力下的分布。且从图12b可明显得出，Arrhenius比Arrhenius广延指数模型每个模块测试结果误差都大。在实验中存在测试误差和同型号不同模块之间的差异，如热阻、导通压降等因素造成部分模块的误差较大，但90%以上测试模块的实验结果误差较小。

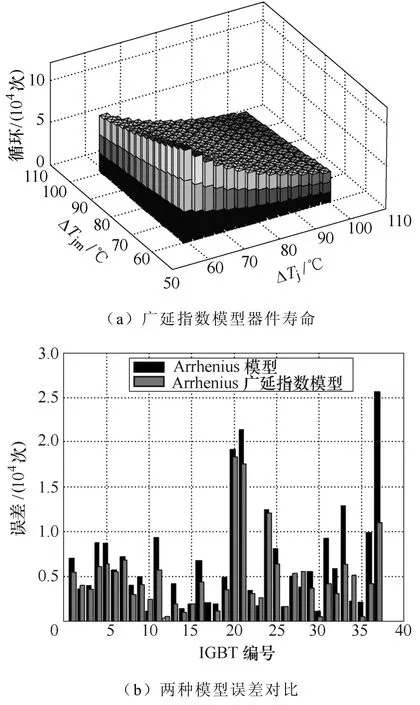
图12 模型结果Fig.12 Results of the model

从建立的器件寿命模型可知，Nf与ΔTj和Tjm均成反比，所以可以通过降低器件结温或改善器件的散热方式（如水冷）来提高器件寿命。由于海上和陆上变流器维修不便，且费用高，精确的寿命模型有利于制定检修计划和降低费用，所以相比Arrhenius模型，Arrhenius广延指数模型更能满足实际需求。为了建立更精确的器件寿命模型，下一步工作将考虑器件开关过程对寿命的影响。

4 结论

本文通过对功率器件在不同应力条件下的功率循环实验，得到模块失效过程的电、热参数变化，并提取了在不同ΔTj、Tjm作用下的失效周期数Nf，利用数理统计方法建立器件一维寿命模型。通过分析可知，该模型存在局限性且未考虑Tjm对器件的影响，所以建立了Coffin-Manson-Arrhenius模型。从Coffin-Manson-Arrhenius模型的结果可知，ΔTj作用远小于Tjm作用，与模块失效理论相悖，且误差较大。在此基础上，提出了Arrhenius广延指数模型，该模型不仅具有更高的精度，而且ΔTj、Tjm的作用效果更符合实际情况。

[1] Wang H, Ma K, Blaabjerg F. Design for reliability of power electronic systems[C]//IECON 38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, 2012: 33-44.

[2] Morozumi A, Yamada K, Miyasaka T, et al. Reliability of power cycling for IGBT power semiconductor modules[J]. IEEE Transactions on Industry Applications, 2003, 39(3): 665-671.

[3] Ramminger S, Wachutka G. Predicting the crack progression in PbSnAg-solder under cyclic loading[C]// 4th International Conference on Integrated Power Systems (CIPS), VDE, Naples, Italy, 2006: 1-6.

[4] Mccluskey F P, Wang Z, Dash M, et al. Reliability of high temperature lead-free solder alternative[C]// IEEE Electronics Systemintegration Technology Conference, Dresden, 2006: 444-447.

[5] Wu W, Held M, Jacob P, et al. Thermal stress related packaging failure in power IGBT modules[C]// Proceedings of the 2nd International Symposium on Power Semiconductor Devices and ICs, ISPSD'95, Yokohama, 1995: 330-334.

[6] 王彦刚, 武力, 崔雪青, 等. IGBT模块封装热应力研究[J]. 电力电子技术, 2000, 34(6): 52-54. Wang Yangang, Wu Li, Cui Xueqing, et al. A study on packaging thermal stress of IGBT modules[J]. Power Electronics, 2000, 34(6): 52-54.

[7] 施建根, 孙伟锋, 景伟平, 等. 车载IGBT器件封装装片工艺中空洞的失效研究[J]. 电子与封装, 2010, 10(2): 23-27. Shi Jiangen, Sun Weifeng, Jing Weiping, et al. Failure analysis of voids in automotive IGBT die attach process[J]. Electronics & Packaging, 2010, 10(2): 23-27.

[8] Ciappa M. Selected failure mechanisms of modern power modules[J]. Microelectronics Reliability, 2002, 42(4-5): 653-667.

[9] Held M, Jacob P, Nicoletti G, et al. Fast power cycling test of IGBT modules in traction application[C]//Proceedings of International Conference on Power Electronics and Drive Systems, 1997, 1: 425-430.

[10] Lu Z, Huang W, Stan M R, et al. Interconnect lifetime prediction for reliability-aware systems[J]. IEEE Transactions on Very Large Scale Integration Systems, 2007, 15(2): 159-172.

[11] Bryant A T, Mawby P A, Palmer P R, et al. Exploration of power device reliability using compact device models and fast electro-thermal simulation[C]//Conference Record of the 2006 IEEE Industry Applications Conference Forty-First IAS Annual Meeting, Tampa, FL, 2006, 3: 1465-1472.

[12] Smet V, Forest F, Huselstein J J, et al. Ageing and failure modes of IGBT modules in high-temperature power cycling[J]. IEEE Transactions on Industrial Electronics, 2011, 58(10): 4931-4941.

[13] 郑利兵, 韩立, 刘钧, 等. 基于三维热电耦合有限元模型的IGBT失效形式温度特性研究[J]. 电工技术学报, 2011, 26(7): 242-246. Zheng Libing, Han Li, Liu Jun, et al. Investigation of the temperature character of IGBT failure mode based on 3D thermal-electro coupling FEM[J]. Transactions of China Electrotechnical Society, 2011, 26(7): 242-246.

[14] Chen M, Hu A, Yang X. Predicting IGBT junction temperature with thermal network component model[C]//Asia-Pacific Power & Energy Engineering Conference, IEEE Computer Society, Wuhan, 2011: 1-4.

[15] 何湘宁, 吴岩松, 罗皓泽, 等. 基于IGBT离线测试平台的功率逆变器损耗准在线建模方法[J]. 电工技术学报, 2014, 29(6): 1-6. He Xiangning, Wu Yansong, Luo Haoze, et al. Quasionline modeling method of the power inverter losses based on IGBT offline test platform[J]. Transactions of China Electrotechnical Society, 2014, 29(6): 1-6.

[16] 贾京, 冯士维, 邓兵, 等. 基于热阻测量的PCB散热特性[J]. 电工技术学报, 2014, 29(9): 239-244. Jia Jing, Feng Shiwei, Deng Bing, et al. Transfer heat performance of PCB based on thermal resistance measurement[J]. Transactions of China Electrotechnical Society, 2014, 29(9): 239-244.

[17] Gachovska T K, Tian B, Hudgins J, et al. A real-time thermal model for monitoring of power semiconductor devices[J]. IEEE Transactions on Industry Applications, 2013, 51(4): 2208-2213.

[18] 刘宾礼, 刘德志, 唐勇, 等. 基于加速寿命试验的IGBT模块寿命预测和失效分析[J]. 江苏大学学报(自然科学版), 2013, 34(5): 556-563. Liu Binli, Liu Dezhi, Tang Yong, et al. Lifetime prediction and failure analysis of IGBT module based on accelerated lifetime test[J]. Journal of Jiangsu University (Nature of Science Edition), 2013, 34(5): 556-563.

[19] 唐勇, 汪波, 陈明, 等. 高温下的IGBT可靠性与在线评估[J]. 电工技术学报, 2014, 29(6):17-23. Tang Yong, Wang Bo, Chen Ming, et al. Reliability and on-line evaluation of IGBT modules under high temperature[J]. Transactions of China Electrotechnical Society, 2014, 29(6): 17-23.

[20] Yang L, Agyakwa P A, Johnson C M. Physicsof-failure lifetime prediction models for wire bond interconnects in power electronic modules[J]. IEEE Transactions on Device & Materials Reliability, 2013, 13(1): 9-17.

[21] Bayerer R, Herrmann T, Licht T, et al. Model for power cycling lifetime of IGBT modules-various factors influencing lifetime[C]//2008 5th International Conference on Integrated Power Systems (CIPS), VDE, Nuremberg, Germany, 2008: 1-6.

[22] Zhang L, Zhao Y, Hou K. The research of levenberg-marquardt algorithm in curve fittings on multiple gpus[C]//2011 IEEE 10th International Conference on Trust, Security and Privacy in Computing and Communications (TrustCom), Changsha, 2011: 1355-1360.

[23] Ciappa M. Selected failure mechanisms of modern power modules[J]. Microelectronics Reliability, 2002, 42(4-5): 653-667.

[24] Hokanson K E, Bar-Cohen A. A shear-based optimization of adhesive thickness for die bonding[J]. IEEE Transactions on Components Packaging & Manufacturing Technology Part A, 1995, 18(3): 578-584.

IGBT Lifetime Model Based on Aging Experiment

Lai Wei1Chen Minyou1Ran Li1Wang Xuemei2Xu Shengyou1
（1. State Key Laboratory of Power Transmission Equipment & System Security and New Technology Chongqing University Chongqing 400044 China 2. School of Electric Power South China University of Technology Guangzhou 510640 China）

According to the IGBT power cycling test, the power device lifetime models based on the device fatigue damage theory are established, to reduce the maintenance cost, enhance the inverter reliability and provide the theoretical support for the inverter maintenance. Firstly, the ageing experiment theory and the extracting parameters method of the power devices were provided. Secondly, according to device fatigue damage theory, power cycling test platform was established and two test plans were designed to obtain the failure parameters of power module. Finally, the one-dimensional lifetime model using Weibull distribution was established. The advantages and disadvantages of this model were analyzed. Compared with the experimental results, the three-dimensional stretched exponential lifetime model is promoted, which is more reasonable than Coffin-Manson and Arrhenius models.

Lifetime model, power cycling, Weibull distribution, Arrhenius stretched exponential model, IGBT

TM46

赖 伟 男，1986年生，博士，研究方向为电力电子器件可靠性和状态监测。

E-mail: laiweicqu@126.com（通信作者）

陈民铀 男，1954年生，教授，博士生导师，研究方向为在线监测与故障诊断。

E-mail: mchencqu@126.com

国家自然科学基金（51477019），国家“111”计划（B08036），中央高校基本科研业务费（CDJZR12150074）和国家重点基础研究发展计划（973计划）（2012CB25200）资助项目。

2014-08-26 改稿日期2014-12-07