板式双边永磁电动悬浮电磁力计算
2017-01-21殷张昆仑
陈 殷张昆仑
(1. 中国中铁二院工程集团有限责任公司 成都 610031 2. 磁浮技术与磁浮列车教育部重点实验室 成都 610031)
板式双边永磁电动悬浮电磁力计算
陈 殷1,2张昆仑2
(1. 中国中铁二院工程集团有限责任公司 成都 610031 2. 磁浮技术与磁浮列车教育部重点实验室 成都 610031)
针对现有电动悬浮模式的缺点,研究了一种由导体板和双边Halbach永磁阵列构成的悬浮系统。相比单边电动悬浮,该系统电磁阻力更小,适用于城市轨道交通。分别采用解析法和有限元法对其产生的电磁力进行计算。首先,建立了空间矢量磁位方程,通过求解该方程可得导体板中涡流分布;其次,研究了空间磁场与涡流的相互作用,得到了电磁力的2D解析表达式,建立了2D和3D有限元模型,计算了不同速度下的电磁力、磁场与涡流,并得出解析法与2D有限元法的平均相对误差为1.7%;最后,通过与单边电动悬浮对比,证明了该悬浮模式可有效提高浮阻比,减小阻力损耗。
双边永磁电动悬浮 Halbach阵列 解析计算 有限元 电磁场
0 引言
当永磁体与导体板发生相对运动时,会在导体板中感生涡流,从而产生悬浮力,这就是永磁电动悬浮的基本原理。这种悬浮方式结构简单,能实现自稳定悬浮,不需要控制,可靠性强,因此已成为磁浮研究的热点。然而传统的永磁电动悬浮方式在低速运行时电磁阻力大且能耗高,因此不适于城市轨道交通。为了克服这一缺点,美国GA公司提出了一种基于双边Halbach阵列的电动悬浮模式[1,2],该方案能有效降低阻力,但悬浮轨道由平行布置的独立线圈构成,结构复杂,安全性较低。为了克服这一缺陷,本文研究了板式双边永磁电动悬浮,并对其电磁场特性和电磁力进行了分析与计算。
这种悬浮方式由非磁性导体板和布置于上下侧的两组Halbach阵列构成,当上下气隙不等时,导体板中将产生感应电流,从而产生悬浮力。在研究永磁体与导体板所构成的电磁装置动态特性时,最常用的是有限元方法(Finite Element Method, FEM)[3-7]。S. M. Jang研究涡流制动器时,建立了较为完整的有限元模型,并设计了相应的实验平台。通常情况下有限元结果准确,但无法反应不同参数间的内在联系。采用解析法研究该类问题时,由于电磁场计算的复杂性,通常假设导体板无限厚或无限薄,从而简化研究问题[8,9]。例如文献[8]在研究单侧电动悬浮时将导体板视为无限薄板,用面电流替代体电流。由于电流趋肤深度与速度关系密切,因此该方法计算结果仅在一个较小的中速区间与实验结果吻合。R. F. Post给出了线圈式电动悬浮的等效电路,通过能量转换理论计算电磁力[10,11],但板式装置等效电感不易计算,因此该方法仅适用于独立线圈式悬浮系统。另外,永磁直线电机具有类似的电磁特性,但永磁电机存在主动控制,次级电流恒定,因此电磁力计算简单,与本文所研究电磁系统有较大差别[12-14]。
本文在上述研究的基础上,提出了板式双边永磁电动悬浮方案,并对其电磁特性与电磁力进行了研究。建立了空间不同区域内磁矢位的微分方程,提出了电磁力的解析式,并用APDL方式建立了参数化的有限元2D、3D模型,证明了该解析式的正确性,对电动悬浮的进一步研究具有重要意义。
1 悬浮系统模型
电动悬浮列车横截面如图1所示,其中永磁阵列为Halbach阵列,该阵列在上下两侧产生不对称磁场,可增加悬浮效率,减小磁场对人体的辐射[8]。
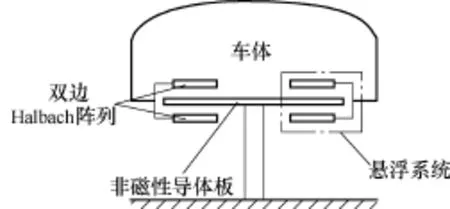
图1 板式双边电动悬浮Fig.1 Plate type null double side permanent magnet electrodynamic suspension
双边永磁电动悬浮示意图如图2所示。通常情况下,为提升悬浮性能,永磁体和导体板横向宽度(W1、W2)远大于极距(τ),此时可将其简化为2D模型。图2中,L为非磁性导体板厚度,h为永磁阵列高度,d1、d2为上、下悬浮间隙。当d1≠d2时,导体板处上、下磁场不对称,在导体板中感应电流,从而产生电磁力。由楞次效应可知,电磁力方向沿d1(d2)方向,故该系统可实现自稳定悬浮。且由图2可知,上、下两组永磁阵列在气隙产生的磁场y分量相互抵消,z分量相互叠加,因此相比单边悬浮,双边悬浮能产生更大浮阻比[15,16]。
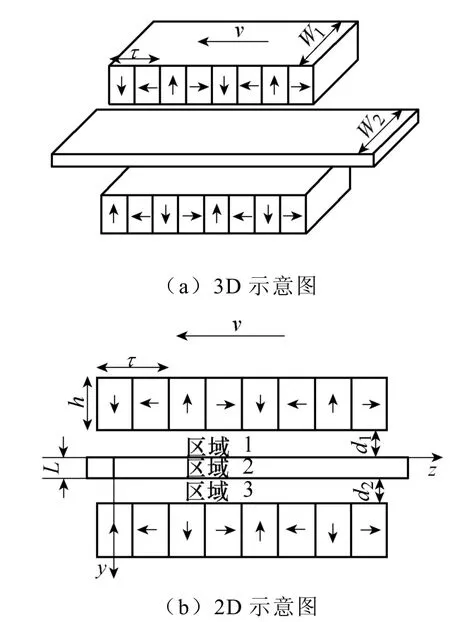
图2 双边永磁电动悬浮示意图Fig.2 Diagrams of double side permanent magnet electrodynamic suspension
2 电磁计算
2.1 解析法计算
单侧Halbach永磁阵列空间磁场表示为[17]
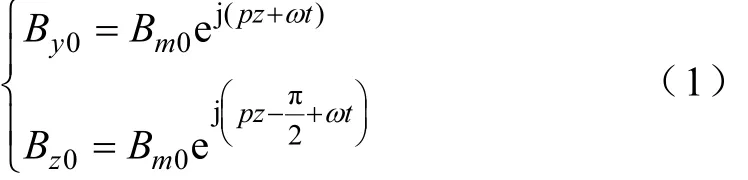
其中
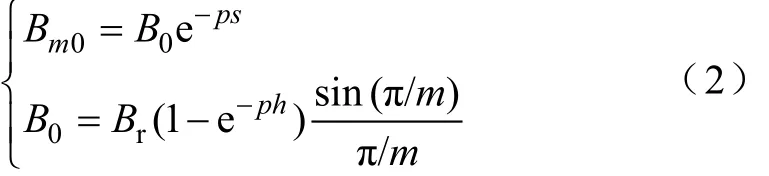
式中,Br为永磁体剩磁;m为一对极中包含的模块数(图1所示为4模块结构,m=4);s为气隙中一点到永磁体下表面的距离;p=π/τ。则双边永磁阵列气隙磁场可表示为


式中,C1~C6为待定常数,由边界条件式(15)、式(19)和式(20)确定。导体板中磁场为永磁体所产生的静态磁场与感生磁场的叠加。故空间中电磁场和涡流可表示为
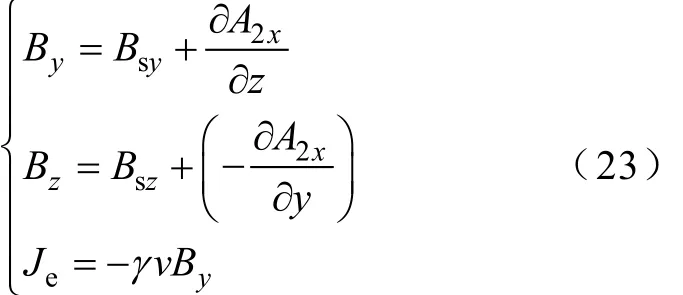
悬浮力和阻力的计算式为
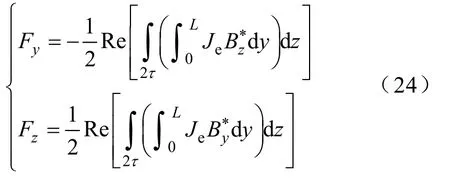
2.2 有限元法计算
本文使用Ansys建立了双边永磁电动悬浮的2D、3D有限元模型,模型参数见表1。2D建模使用的单元为PLANE53,用实常数法定义运动速度,考虑到模型中材料均为线性特性,故采用Solve线性求解方法。生成节点数114 042,单元数37 723。为节省计算空间和时间,采用3D对称建模,3D有限元模型如图3所示,使用单元为Solid97,生成节点数为143 876,单元数为126 720。运行速度为200km/h时,导体板中磁感线和涡流分布分别如图4和图5所示。
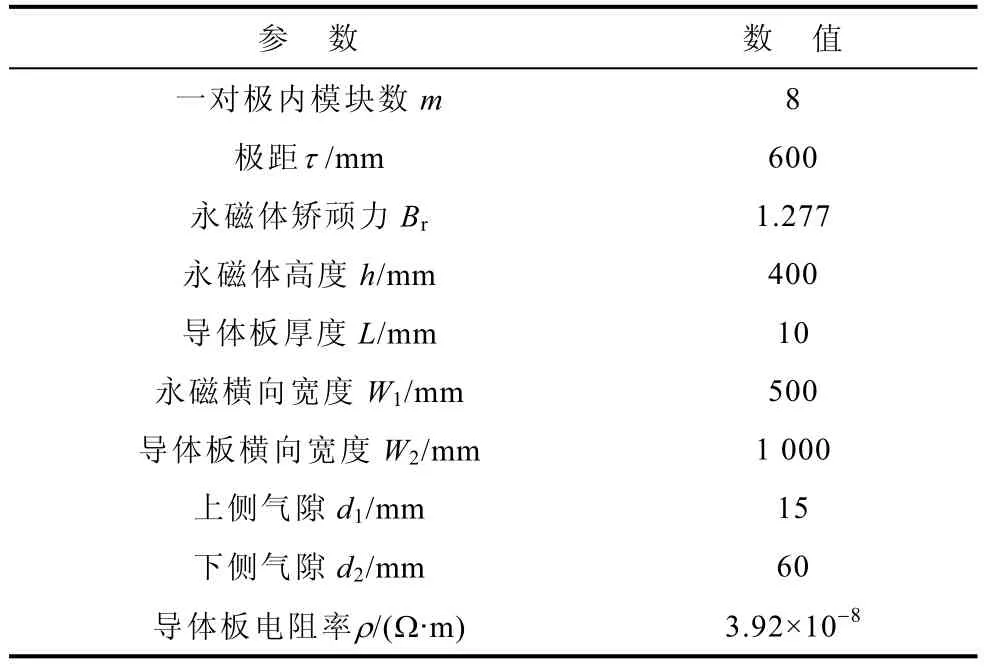
表1 模型参数Tab.1 Model parameters
3 结果分析
3.1 电磁力
本文分别采用解析模型和有限元模型进行计算,参数见表1,所得悬浮力与阻力随速度变化关系如图6所示。
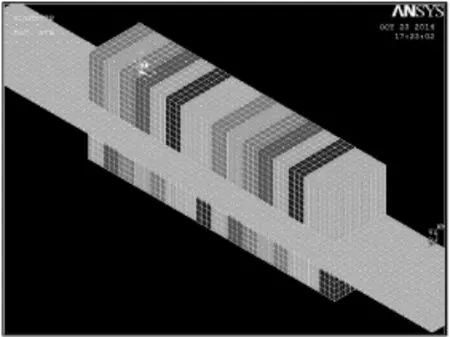
图3 3D有限元模型Fig.3 3D finite element model
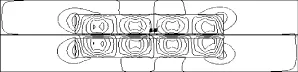
图4 200km/h速度时的磁感线分布Fig.4 Distribution of magnetic induction line at speed of 200km/h
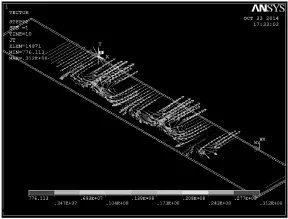
图5 导体板中涡流分布Fig.5 Distribution of eddy current in the conductor plate
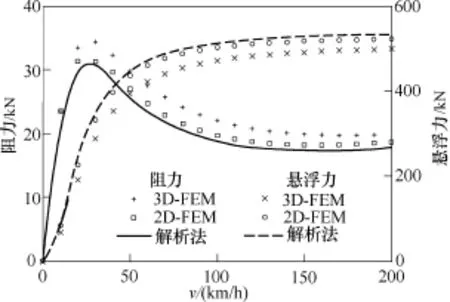
图6 悬浮力与阻力随速度变化关系Fig.6 Relationship between levitation force and resistance change with velcity
图7为不同速度下解析法和有限元法计算的相对误差,由图可知,解析模型计算结果与2D有限元模型计算结果几乎一致,两者最大相对误差4.1%,平均相对误差1.7%,其中悬浮力最大相对误差仅为2.2%。而解析法与3D有限元法计算平均误差为9.2%。由图4可知,3D模型中导体板中存在横向(z方向)电流,这与2D计算的前提假设不符,因此产生误差。
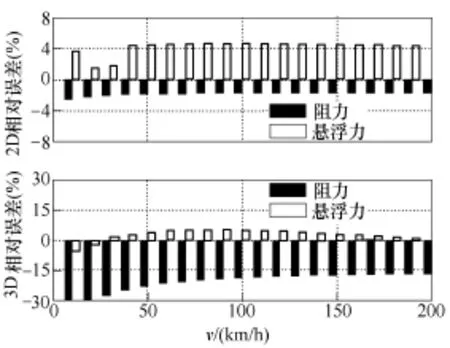
图7 解析与有限元法计算相对误差Fig.7 Relative error between the analytic and finite element methods
本文分别在不同横向宽度与极距比下,计算了3D有限元法与解析法的相对误差,结果如图8所示。由图8可知,随着横向宽度与极距比增加,两者相对误差下降,当横向宽度与极距比为3∶1时,相对误差约为5.1%。因为当横向宽度增加时,横向端部效应可忽略,导体板中电流横向分量(z分量)为零,故可将模型简化为2D计算,在实际应用中,该假设显然是成立的。
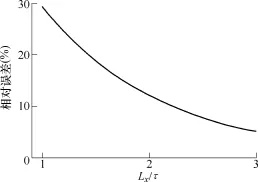
图8 三维有限元法与解析法的相对误差随Lx/τ比值的变化关系Fig.8 Relative error between 3D FEM and expression method vs.Lx/τ
3.2 磁场与涡流
为了进一步对解析模型进行说明,本文对比了解析法和有限元法磁场与涡流的计算结果。其中解析计算式为式(23),有限元结果可由Ansys直接得出。图9和图10分别为速度200km/h时,y=0处磁场和导体板不同深度下涡流分布。
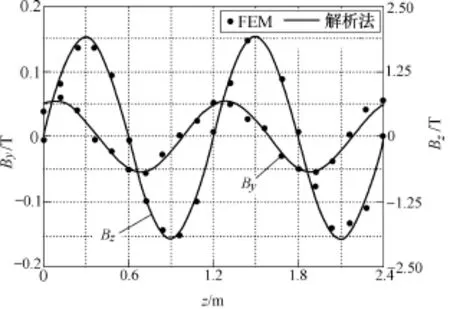
图9 速度200km/h时y=0处磁场Fig.9 Magnetic field with velocity of 200km/h aty=0
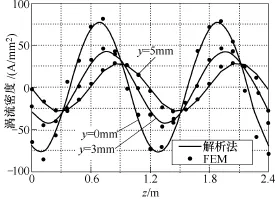
图10 导体板不同深度下涡流分布Fig.10 Eddy current distribution at different depth of conductor plate
如图9和图10所示,解析法与有限元计算法在阵列中部有较高的吻合度,而在端部相对误差较大,这是由于Halbach阵列磁场的正弦假设,忽略了端部效应造成的。
3.3 单边与双边电动悬浮对比
本文所研究的双边电动悬浮是为提高单边电动悬浮浮阻比提出的,为检验这一效果,根据表1中参数,对两种悬浮方式不同速度下的浮阻比进行计算。单边与双边悬浮浮阻比对比如图11所示,单边模型中没有下方永磁阵列,故无d2,其余参数均相同。由图10可知,双边悬浮能极大地提高了浮阻比,从而减小了阻力损耗,因此该系统比传统悬浮模式更适于城市轨道交通。
4 结论
针对现有电动悬浮存在的缺陷,提出了板式双边永磁电动悬浮方案。通过求解空间矢量磁位方程,得到了磁场与涡流分布,进而推导出该悬浮系统电磁力的2D解析计算,并用有限元法证明了所得解析式的正确性。同时对比了相同结构下,单边与双边悬浮的浮阻比,证明了该方案用于城市轨道交通的优越性。本文假设合理,推导严密,结果准确,对永磁电动悬浮的进一步研究具有重要意义。
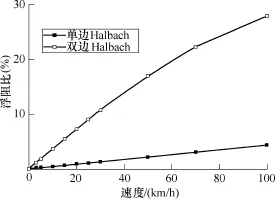
图11 单边与双边悬浮浮阻比对比Fig.11 Comparation of levitation-to-drag ratio in single and double suspension system
[1] Kratz R, Post R F. A current electro-dynamic levitation system[J]. IEEE Transctions on Applied Superconductivity, 2002, 12(1): 930-932.
[2] 武瑛, 严陆光, 徐善纲. Inductrack磁浮技术及其在磁浮列车系统中的应用[J]. 电气应用, 2006, 25(1): 1-3. Wu Ying, Yan Luguang, Xu Shangang. Inductrack technology and its application in maglev transport[J]. Electric Application, 2006, 25(1): 1-3.
[3] Jang S M, Lee S H, Jeong S S. Characteristics analysis of eddy-current brake system using the linear Halbach array[J]. IEEE Transactions on Magnetics, 2002, 38(9): 2994-2996.
[4] Jang S M, Kwon J K, Lee S H, et al. Characteristic analysis of linear eddy-current brakes[C]//ICEMS 2003 Sixth International Conference on Electrical Machines and Systems, Beijing, 2003: 177-179.
[5] 赵玫, 邹继斌, 王骞, 等. 圆筒型横向磁通永磁直线电机的基础研究[J]. 电工技术学报, 2014, 29(增1): 80-89. Zhao Mei, Zou Jibin, Wang Qian, et al. Fundamental research of tubular transverse flux permanent magnet linear machine[J]. Transactions of China Electrotechnical Society, 2014, 29(S1): 80-89.
[6] 汤平华, 漆亚梅, 黄国辉, 等. 定子无铁心飞轮电机绕组涡流损耗分析[J]. 电工技术学报, 2010, 25(3): 27-32. Tang Pinghua, Qi Yamei, Huang Guohui, et al. Eddy current loss analysis of ironless flywheel electric machine’s winding[J]. Transactions of China Electrotechnical Society, 2010, 25(3): 27-32.
[7] 黄宇淇, 方宾义, 孙锦枫. 飞轮储能系统应用于微网的仿真研究[J]. 电力系统保护与控制, 2011, 39(9): 83-113. Huang Yuqi, Fang Bingyi, Sun Jingfeng. Simulation research on the microgrid with flywheel energy storage system[J]. Power System Protection and Control, 2011, 39(9): 83-113.
[8] 李春生, 杜玉梅, 夏平畴, 等. 直线型Halbach磁体和导体板构成的电动式磁悬浮系统的分析及实验[J]. 电工技术学报, 2009, 24(1): 18-22. Li Chunsheng, Du Yumei, Xia Pingchou, et al. Analysis and experimental testing of EDS maglev with linear Halbach and conducting sheet[J]. Transactions of China Electrotechnical Society, 2009, 24(1): 18-22.
[9] 王江波, 李耀华, 严陆光. 直线Halbach磁体用于磁浮列车涡流制动的研究[J]. 电气传动, 2010, 40(5): 8-11. Wang Jiangbo, Li Yaohua, Yan Luguang. Study on applying the linear Halbach array to eddy current brake system for maglev[J]. Electric Drive, 2010, 40(5): 8-11.
[10] Post R F, Ryutov D D. The inductrack: a simpler approach to magnetic levitation[J]. IEEE Transactions on Applied Superconductivity, 2000, 10(1): 901-904.
[11] Murai T, Hasegawa H. Electromagnetic analysis of inductrack magnetic levitation[J]. Electrical Engineering in Japan, 2003, 142(1): 67-74.
[12] 黄学良, 张前, 周赣. 一种无铁Halbach型永磁直线电机[J]. 电工技术学报, 2010, 25(6): 1-6. Huang Xueliang, Zhang Qian, Zhou Gan. Halbach permanent magnet ironless linear motors[J]. Transactions of China Electrotechnical Society, 2010, 25(6): 1-6.
[13] 孟鹏, 邱晓燕, 林伟, 等. 直驱式永磁同步风力发电动态特性的研究[J]. 电力系统保护与控制, 2012,40(14): 38-43. Meng Peng, Qiu Xiaoyan, Lin Wei, et al. Study of the dynamic characteristics of directly driven permanent magnet synchronous wind turbine[J]. Power System Protection and Control, 2012, 40(14): 38-43.
[14] 范坚坚, 吴建华, 李创平, 等. 分块式Halbach型磁钢的永磁同步电机解析[J]. 电工技术学报, 2013, 28(3): 36-42. Fan Jianjian, Wu Jianhua, Li Chuangping, el al. Solution of permanent magnet synchronous motors with partition between poles Halbach magnet[J]. Transactions of China Electrotechnical Society, 2013, 28(3): 36-42.
[15] Cho H W, Han H S, Bang J S, et al. Characteristic analysis of electrodynamic suspension device with permanent magnet Halbach array[J]. Journal of Applied Physics, 2009, 105(7): 3141-3143.
[16] He Guang, Long Zhiqiang, Cheng Yuwei. The development and application of permanent-magnet EDS based on Halbach structure[C]//29th Chinese Control Conference, Beijing, 2010: 5457-5462.
[17] Hoburg J F. Modeling maglev passenger compartment static magnetic field from linear Halbach permanent magnet arrays[J]. IEEE Transactions on Magnetics, 2004, 40(1): 59-64.
[18] 宋玉晶, 张鸣, 朱煜. Halbach永磁阵列磁场解析求解及推力建模[J]. 电工技术学报, 2014, 29(11): 61-67. Song Yujing, Zhang Ming, Zhu Yu. Modeling of Halbach array magnetic field and motor thrust[J]. Transactions of China Electrotechnical Society, 2014, 29(11): 61-67.
[19] 陈殷, 张昆仑, 胡巧琳. 基于盘式Halbach永磁阵列的重力平衡装置电磁力计算[J]. 电工技术学报, 2014, 29(5): 36-42. Chen Yin, Zhang Kunlun, Hu Qiaolin. Calculating electromagnetic force created by gravity balance device based on discal Halbach permanent magnet array[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 36-42.
[20] 郭思源, 周理兵, 齐歌. 双三相永磁同步电机电磁性能解析计算[J]. 电工技术学报, 2014, 29(5): 17-28. Guo Siyuan, Zhou Libing, Qi Ge. Analytical calculation of electromagnetic performance in dual three-phase permanent magnet brushless AC machines[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 17-28.
Calculation of Electromagnetic Force of Plate Type Null Double Side Permanent Magnet Electrodynamic Suspension
Chen Yin1,2Zhang Kunlun2
(1. Chinese China Railway Eryuan engineering Refco Group Ltd Chengdu 610031 China 2. Key Laboratory of Magnetic Suspension Technology and Maglev Vehicle Ministry of Education Chengdu 610031 China)
In view of the existing weaknesses, a new suspension system, composed of conducting sheet and double Halbach array, was proposed in this paper. Compared with single Halbach array system, this device could create least drag force, and it is more suitable for urban transportation. Analytic and finite element methods were used to calculate the forces created by this device. First, the differential equations of magnetic vector potentials were built, and accordingly the distribution of eddy current can be deduced. Second, in order to get the expression of forces, the relationship between magnetic field and current was studied. 2D and 3D finite element models were built. The magnetic forces, field and eddy current in different velocities were calculated. The relative error between analytic method and 2D FEM is 1.7%. At last, compared with single Halbach suspension system, the levitation-to-drag ratio highly increased in this model.
Double side permanent magnet electrodynamic suspension, Halbach array, analytic calculation, finite element, electromagnetic field
TM154.1
陈 殷 男,1987年生,博士研究生,研究方向为电磁悬浮。
E-mail: chenyin_swjtu@126.com(通信作者)
张昆仑 男,1964年生,教授,博士生导师,研究方向为电力电子与电力传动、电磁悬浮与线性驱动等。
E-mail: zhangkunlun@home.swjtu.edu.cn
中央高校基本科研业务费(2682013ZT18)和2014年西南交通大学博士研究生创新基金资助项目。
2014-09-10 改稿日期2014-10-28
