具零阶耗散的双成分Camassa-Holm方程的整体解和爆破现象

朱师师,臧林恩

(云南师范大学数学学院,云南昆明650500)

具零阶耗散的双成分Camassa-Holm方程的整体解和爆破现象

朱师师,臧林恩

(云南师范大学数学学院,云南昆明650500)

本文研究了具零阶耗散的双成分Camassa-Holm方程的Cauchy问题.由Kato定理得到局部适定性的结果,然后研究了解的整体存在性和爆破现象.

双成分Camassa-Holm方程;零阶耗散;局部适定性;爆破;整体存在性

1 引言

近年来,Camassa-Holm方程(CH方程)

(其中ω是任意常数)得到广泛关注.它是一类描述浅水区域中单向传播波的运动模型.CH方程是一类完全可积系统,它有一对相应的Lax对[1],具有双Hamilton结构[2].该方程由于其一些显著特征而被广泛关注.当ω=0时,该方程具有形如u(x,t)=ce-|x-ct|的孤立波解(其中c为任意常数).当c0时,这种孤立波解在有限速度内行进,且在波峰处不光滑(它的一阶导含有一个跳跃间断点),即出现了尖点,又称孤立尖解[3].Constantin等研究了该方程尖孤立子的稳定性和相互碰撞问题,证实了这种孤立子和KdV方程的孤立子一样,具有碰撞后不改变其形状和速度等性质.CH方程另一显著特征,既能描述孤立子又能描述波的破裂现象[1,4].CH方程的短波极限形式就是Hunter-Saxton(HS)方程

该方程描述的是线状液态晶体波的传播.

CH方程和HS方程有许多可积的多成分推广[5-9],其中最著名的是

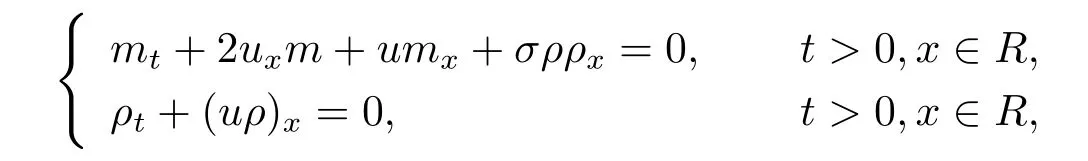
其中m=u-uxx,σ=±1,CH方程可由ρ≡0得到.它是一个完全可积系统.在文[8]中, Constantin和Ivanov从浅水波理论的角度导出该系统,并研究了它的整体解和某些爆破解.最近,该系统的数学性质被许多文章进一步研究,例如文[5,6,8]等.

在实际情况下,能量耗散是自然界不可避免的现象,这在波的传播过程中也经常发生,因此研究耗散项对水波方程的影响是很有必要的.早在1970年,Ott和Sudan就研究了能量耗散对KdV方程的解的影响.在1988年,Ghidaglia把弱耗散的KdV方程作为有限维动力系统的一个模型,来研究该方程解的长时间性态.

带耗散项的双成分CH方程具有如下形式

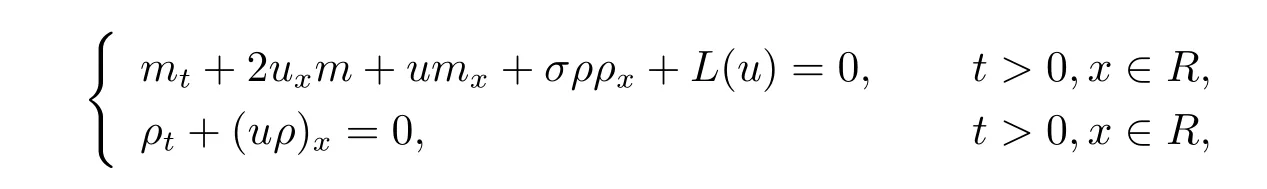
其中m=u-uxx,σ=±1,L(u)是耗散项.根据不同的物理背景,L可以是一个微分算子或是一个拟微分算子.本文研究下面具零阶耗散的双成分CH方程的Cauchy问题

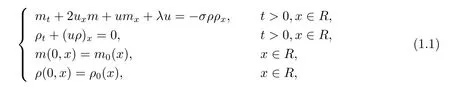
其中m=u-uxx,σ=±1,λ是一个大于0的固定常数.

在第二节,将应用Kato理论证明方程(1.1)的局部适定性.在第三节研究方程(1.1)的解的爆破现象.最后,在第四节研究了方程(1.1)的整体解.

下面给出本文常用的一些记号.用‖·‖Hs,‖·‖L∞,‖·‖Lp分别表示Hs(R),L∞(R), Lp(R)空间的范数;(·,·)s表示Hs(R)空间的内积;‖·‖X表示Banach空间X上的范数.

2 局部适定性

本节用Kato定理证明出方程(1.1)的解的局部适定性定理.先叙述Kato定理,考虑抽象的拟线性发展方程

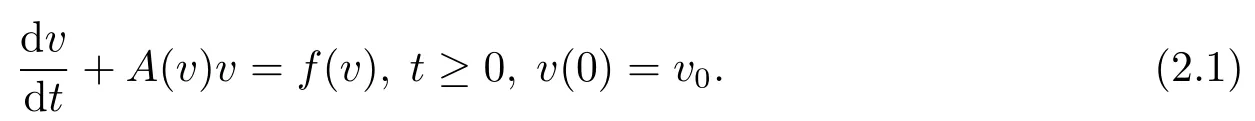
设X,Y是两个Hilbert空间,Y连续嵌入到X,且嵌入是稠密的,从Y到X有一个微分同胚Q:Y→X,‖·‖X和‖·‖Y表示Banach空间X,Y的范数,L(Y,X)表示从Y到X的全体有界线性算子空间(当X=Y时,记为L(X)).假设

(i)∀y∈Y,A(y)∈L(Y,X),且

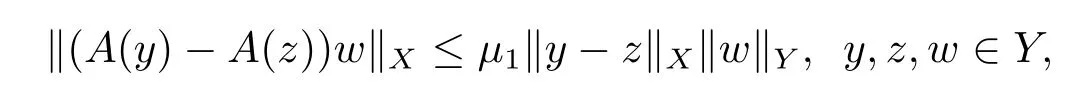
且∃β∈R,A(y)∈G(X,1,β)在Y上一致有界.

(ii)QA(y)Q-1=A(y)+B(y),其中B(y)∈L(X)在Y上一致有界,且

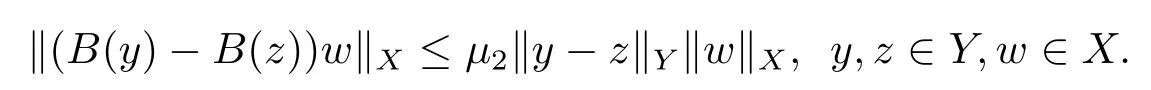
(iii)f:Y→Y在Y上一致有界,且

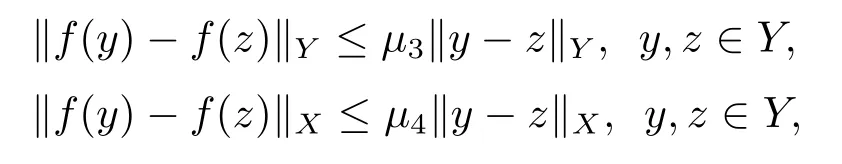
这里µ1,µ2,µ3,µ4是仅依赖于max{‖y‖Y,‖z‖Y}的常数.

定理2.1[10]在条件(i)–(iii)下,对于v0∈Y,存在一个仅依赖于‖v0‖Y的最大时间T＞0,使得方程(1.1)在[0,T)存在唯一解v,并满足v=v(·,v0)∈C([0,T);Y)∩C1([0,T);X),且映射v0→v(·,v0)从Y到C([0,T);Y)∩C1([0,T);X)是连续的.

下面将方程(1.1)变形,以便应用Kato定理证明其解的局部适定性.注意在流体动力学的推导过程中,当|x|→∞时,u(t,x)→0,ρ(t,x)→1,∀t∈R.令=ρ-1,则当|x|→∞时,取σ=1,方程(1.1)化为

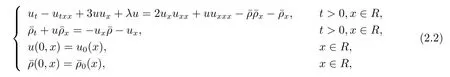
或

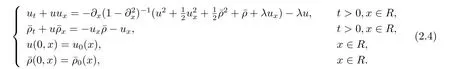
定理2.2设z0=≥2,则存在一个最大时间T=T(‖z0‖Hs×Hs-1)＞ 0,使得方程(2.3)在区间[0,T)存在唯一解z=,并满足

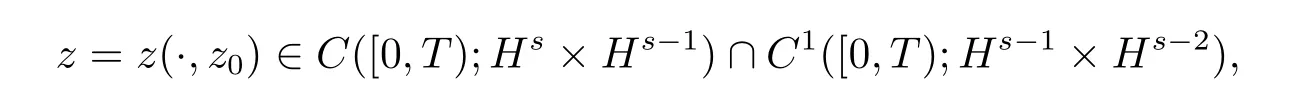
且解连续依赖于初值z0,即映射

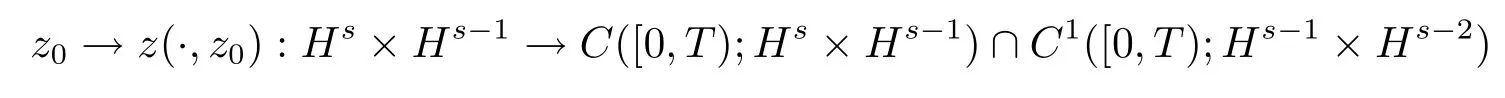
是连续的.

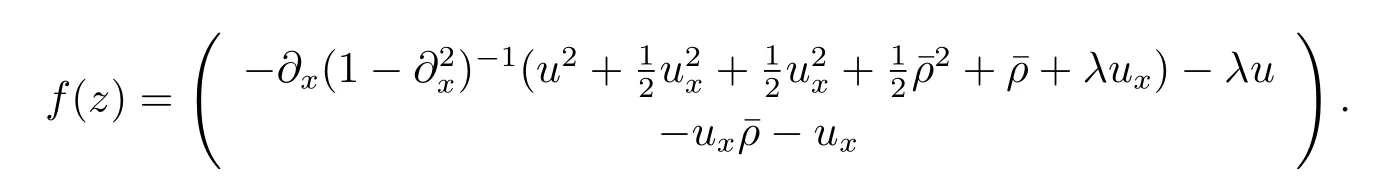
又设Y=Hs×Hs-1,X=Hs-1×Hs-2,Λ=和Q=显然,Q是 Hs×Hs-1到Hs-1×Hs-2上的一个同胚映射.为证明定理2.2,仅需要证明A(z)和f(z)满足Kato定理中的条件(i)–(iii).

下面将定理2.2的证明分成几个引理完成.

引理2.1[11]设X1和X2是Banach空间,且Ai∈G(Xi,1,β),i=1,2,则算子

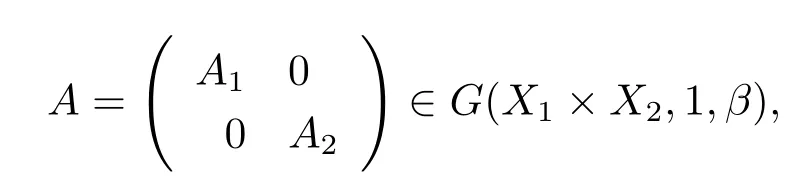
其中D(A)=D(A1)×D(A2).

引理2.2[5,12]设u∈Hs,s≥2,则算子A(u)=u∂x∈G(Hs-1,1,β).

由引理2.1–2.2得到

引理2.3设z∈Hs×Hs-1,s≥2,则算子A(z)=∈G(Hs-1× Hs-2,1,β).

引理2.4[7,8]设A(z)=,z∈Hs×Hs-1,s≥2,则A(z)∈L(Hs× Hs-1,Hs-1×Hs-2),且满足

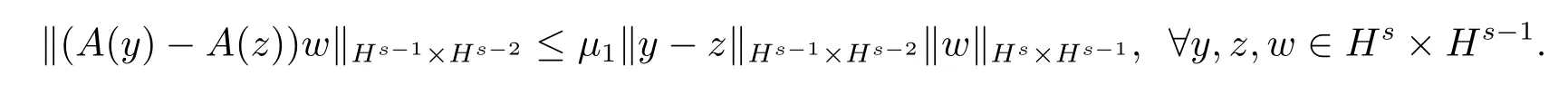
引理2.5[7,8]设B(z)=QA(z)Q-1-A(y),z∈Hs×Hs-1,s≥2,则

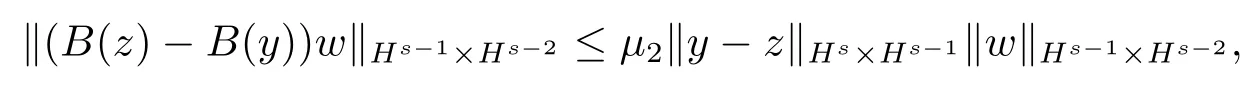
∀y,z∈Hs×Hs-1,w∈Hs-1×Hs-2.

引理2.6[10]设r,t为满足-r＜t≤r的实数,则

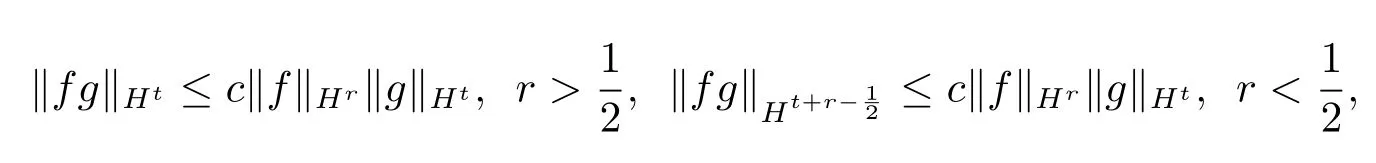
其中c只为依赖于r,t的正常数.

现证明在定理2.2中f满足条件(iii).

引理2.7设z∈Hs×Hs-1,s≥2,

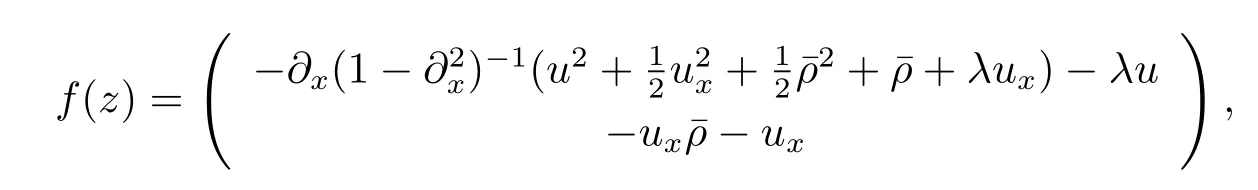
则f在Hs×Hs-1上有界,且满足

(a)‖f(y)-f(z)‖Hs×Hs-1≤µ3‖y-z‖Hs×Hs-1,y,z∈Hs×Hs-1,

(b)‖f(y)-f(z)‖Hs-1×Hs-2≤µ4‖y-z‖Hs-1×Hs-2,y,z∈Hs×Hs-1.

证设y,z∈Hs×Hs-1,s≥2.注意Hs-1是Banach代数,则

这就完成了对(a)式的证明.其中,在上述不等式中令y=0,就能够得到f在Hs×Hs-1上是有界的.

接下来证明(b)式,

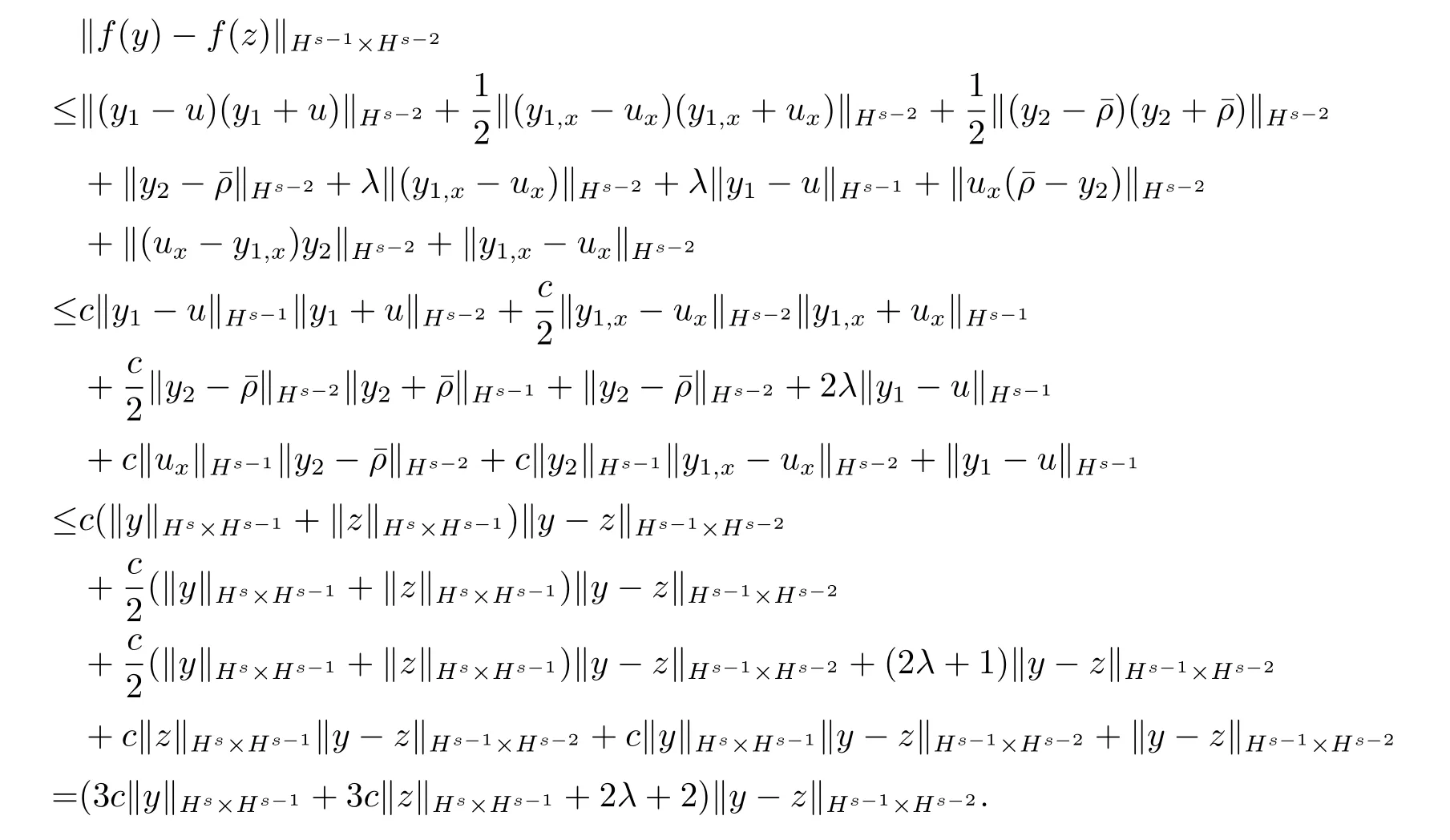
上述估计过程中需用到引理2.6(r=s-1,t=s-2的情形).于是(b)式得证.

综合引理2.1–2.5和引理2.7,应用定理2.1,定理2.2得证.

3 爆破

这节中将证明方程(2.2)解爆破的充要条件,并给出导致解发生爆破的两个充分条件.

引理3.1[13]若r＞0,则Hr∩L∞是Banach代数,且

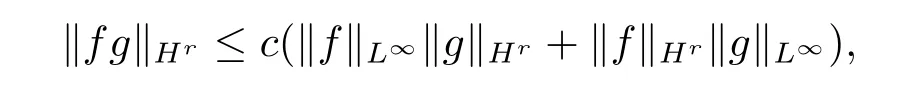
其中c只为依赖于r的常数.

引理3.2[13]若r＞0,则

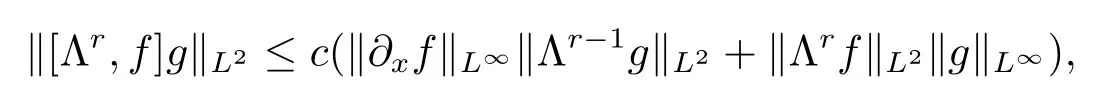
其中c只为依赖于r的常数.

引理3.3设z0=∈Hs×Hs-1,s≥2,且T＞0是方程(2.2)相应解的最大存在时间,则∀t∈[0,T),有

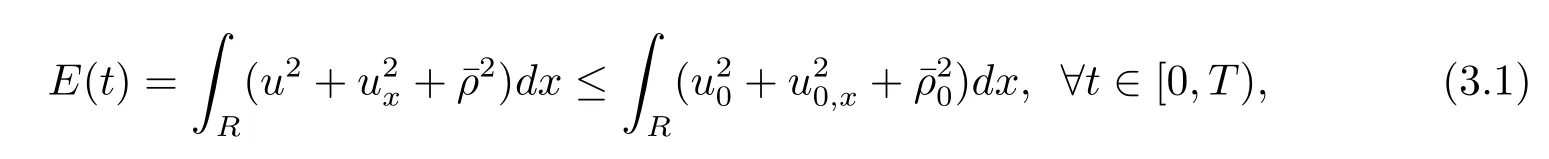
且

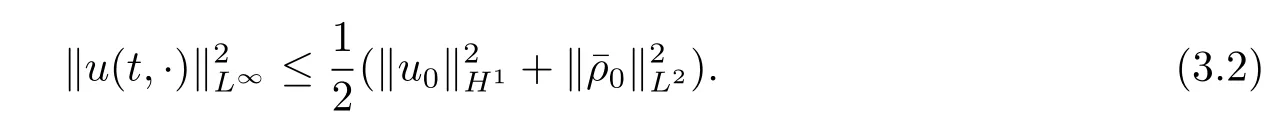
证运用定理2.2及稠密性定理,只需证明上述定理对某个s≥2成立即可.这里假设s=3来证明上述定理,在方程(2.3)中,对第一个方程关于x求偏导,再运用恒等式得到

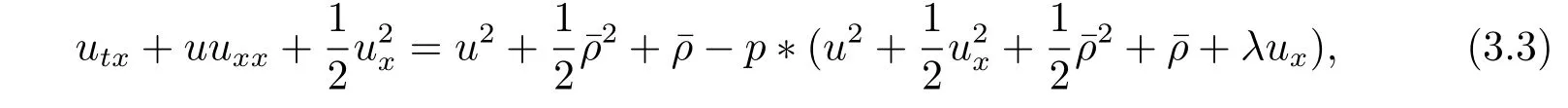
其中f=u2+根据方程(2.3)及(3.3)式,再分部积分得到

所以(3.1)式得证.

根据上述不等式,得到

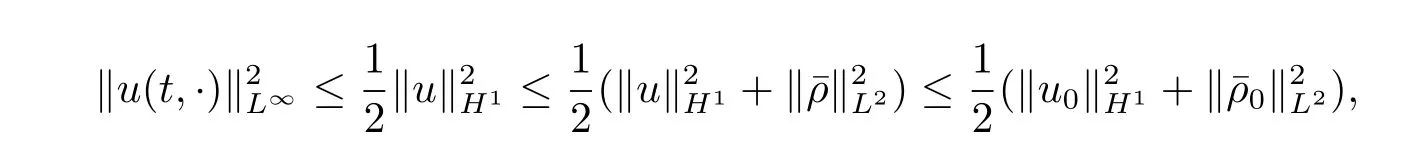
这就完成了对引理3.3的证明.

由引理3.1–3.3可得到下述重要结论.

定理3.1设z0=∈Hs×Hs-1,s≥2,且T是方程(2.3)关于初始值z0的解的最大存在时间,若存在M＞0,使得

证根据定理2.2,设z=是方程(2.3)关于初始值z0∈Hs×Hs-1,s≥2,的解,且T是相应解z的最大存在时间.证明过程中,c＞0是仅依赖于s的正常数.对方程(2.4)中第一个方程运用算子Λs,且两边同时乘以Λsu,再关于R积分,得到

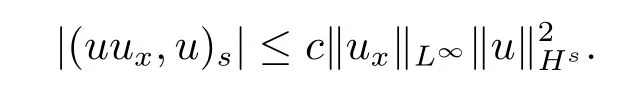
其次,估计(3.4)式右边的第二个式子

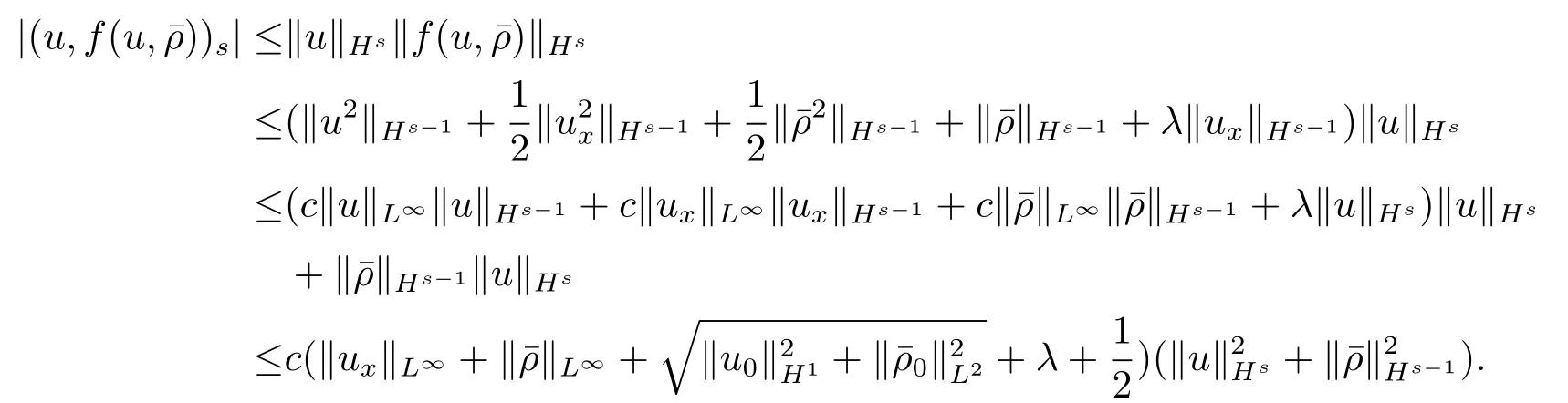
上述估计过程需用到引理3.1(r=s-1的情形)和(3.2)式.最后,估计(3.4)式右边的第三个式子

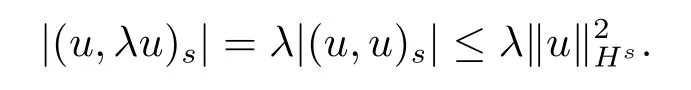
结合上述三个不等式及(3.4)式,得到

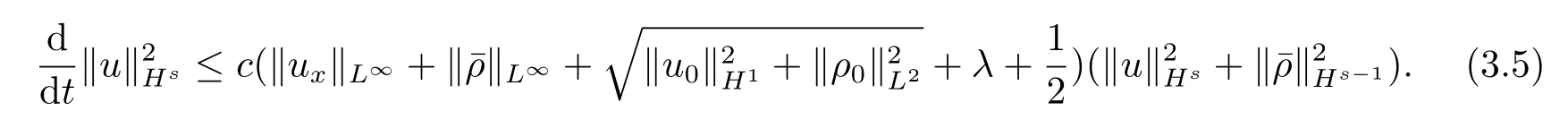
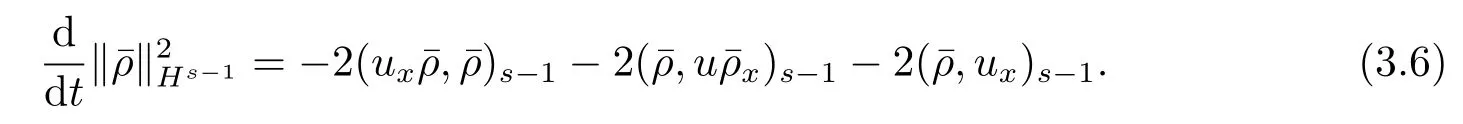
现首先估计(3.6)式右边的第一个式子和第二个式子(参见文[14]定理3.1)得到

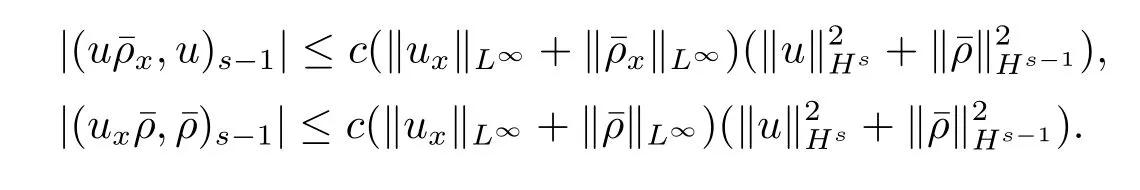
再估计(3.6)式右边的第三个式子,得到

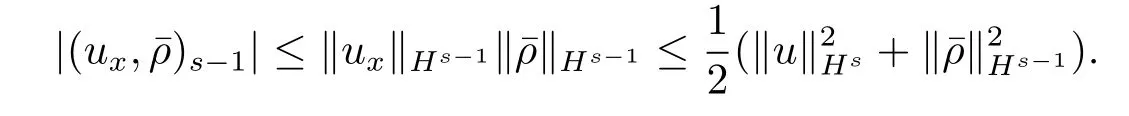
结合上述三个不等式及(3.6)式,得到

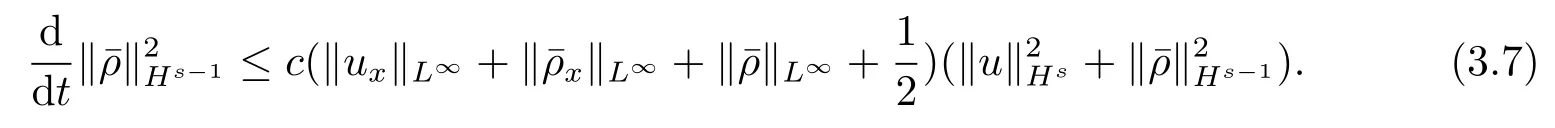
根据(3.5)–(3.7)式,得到

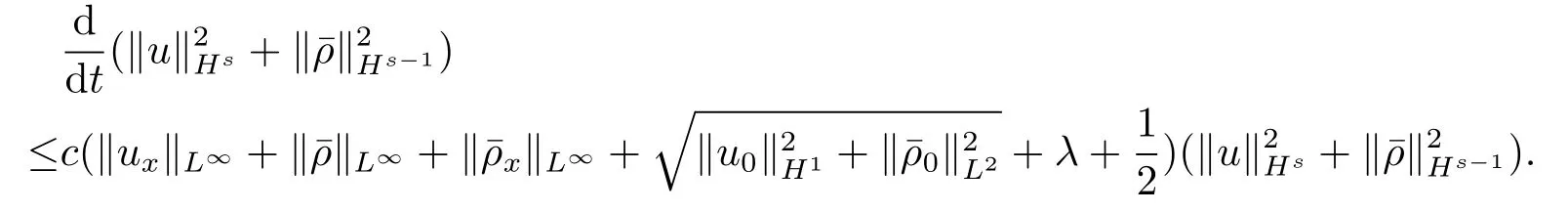
运用Gronwall不等式和定理已给出的假设条件,得到

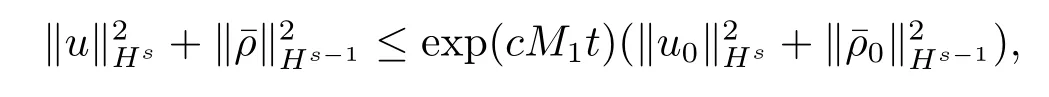
为研究方程(2.2)的解的精确的爆破机制,引入如下初值问题

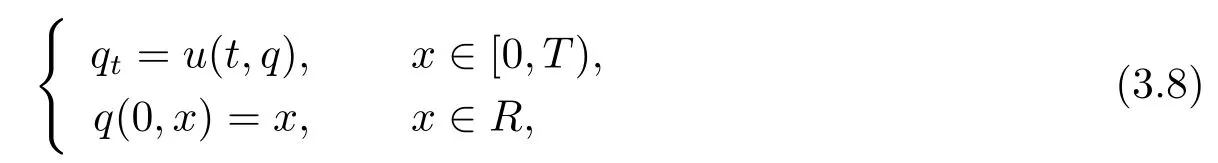
其中u表示方程(2.3)的解的第一个元素,且是局部Lipschitz连续函数.应用常微分方程的一些结论,能够得到关于q的两个结论,这两结论在研究爆破现象中非常重要.

引理3.4[15,16]设u∈C([0,T);Hs)∩C1([0,T);Hs-1),s≥2,则方程有唯一解q∈C1([0,T)×R;R),且q(t,·)是R上的一个递增微分同胚映,满足

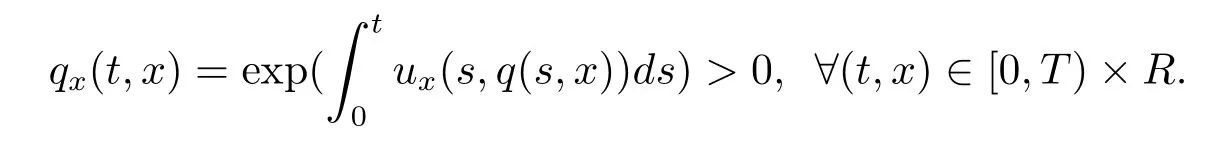
引理3.5设z0=∈Hs×Hs-1,s≥2,且T＞0是方程(2.3)相应解的最大存在时间,则

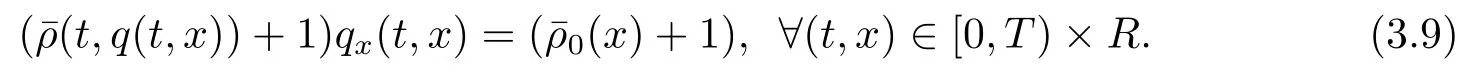
此外,若存在M＞0,使得∀(t,x)∈[0,T)×R,有ux(t,x)≥-M,则

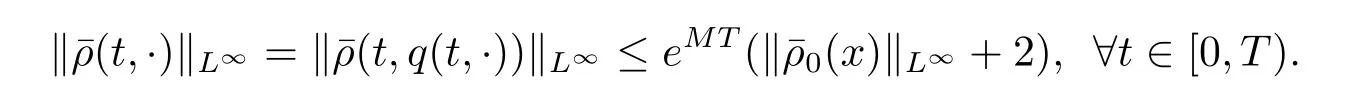
证(参见文[6]引理2.5)得到=0.根据引理3.4和(3.9)式及引理给出的假设条件,得到

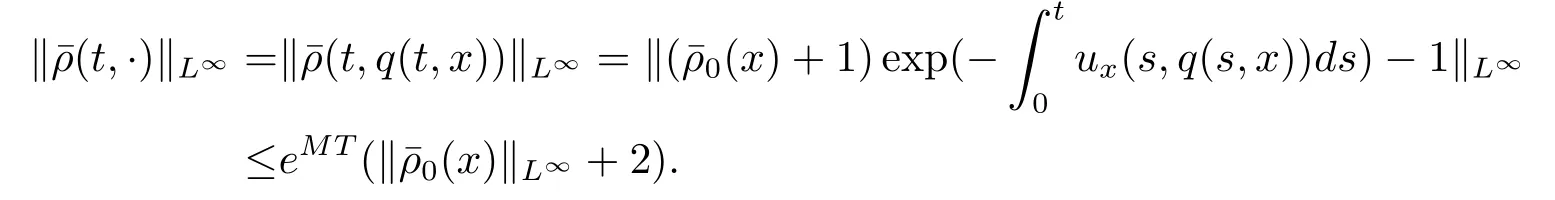
这就完成了引理3.5的证明.

根据定理3.1和引理3.5,可以得到以下推论.

推论3.1设z0=∈Hs×Hs-1,s≥2,且T是方程(2.3)关于初始值z0的解的最大存在时间,若存在M＞0,使得

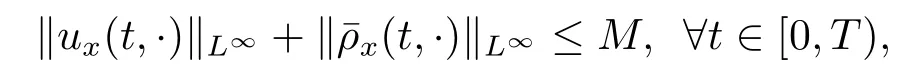
则解z(t,·)关于范数‖·‖Hs×Hs-1在[0,T)内不会爆破.

接下来将要证明方程(2.3)解的精确的爆破机制.

定理3.2设z0=且T是方程(2.3)关于初始值z0的解的最大存在时间,则方程的解在有限时间内爆破当且仅当

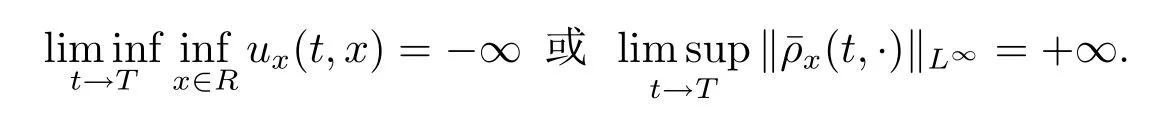
证根据定理2.2,设z=是方程(2.3)关于初始值z0∈Hs×Hs-1(s≥2)的解,且T是相应解z的最大存在时间.用m=u-uxx同时乘以方程(2.2)的第一个方程的两边,然后再分部积分,得到

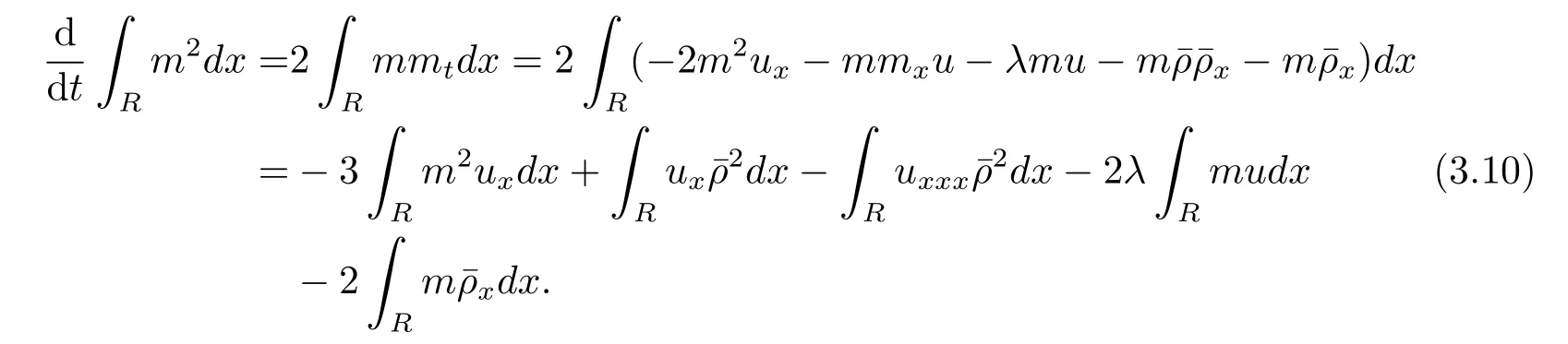
对方程(2.2)的第一个方程关于x求偏导,然后方程两边同时乘以mx=ux-uxxx,最后再积分,得到

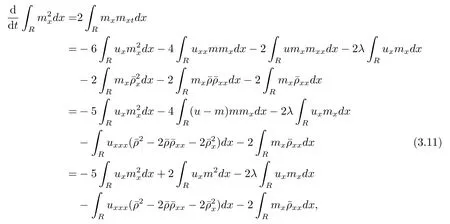
这里用到了关系式m=u-uxx和=0.结合(3.10)–(3.11)式,得到

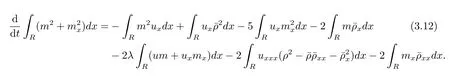
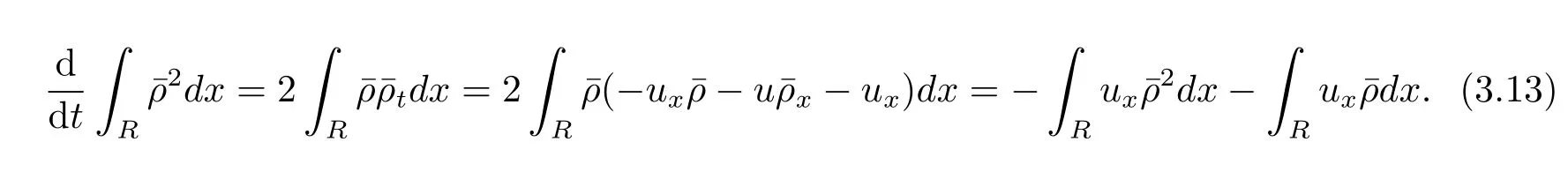
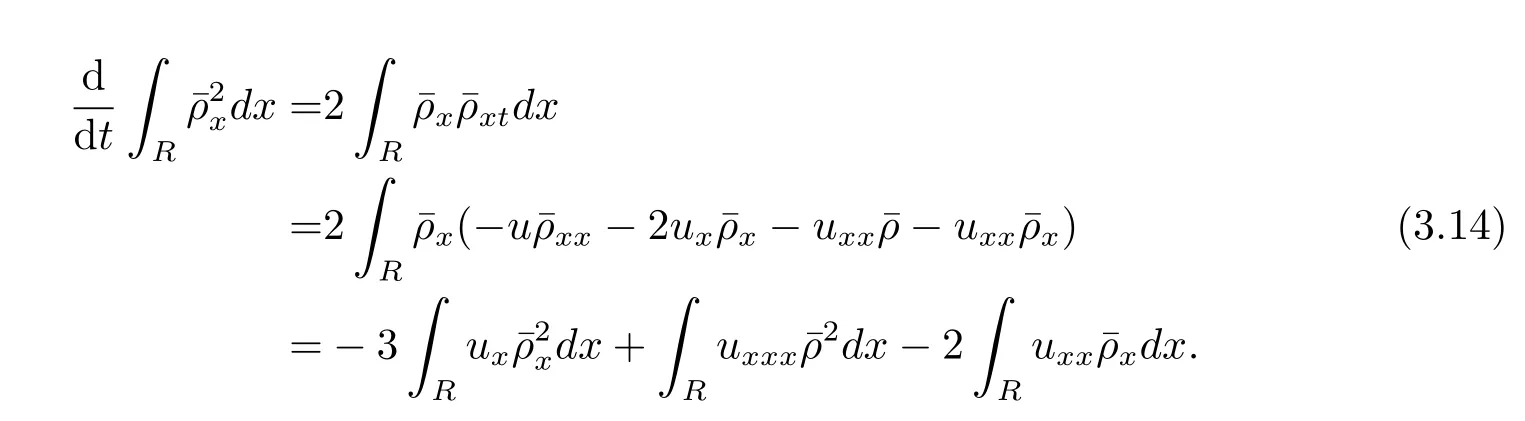
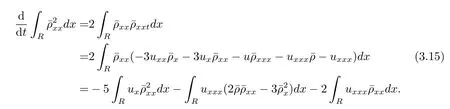
结合(3.12)–(3.15)式,得到

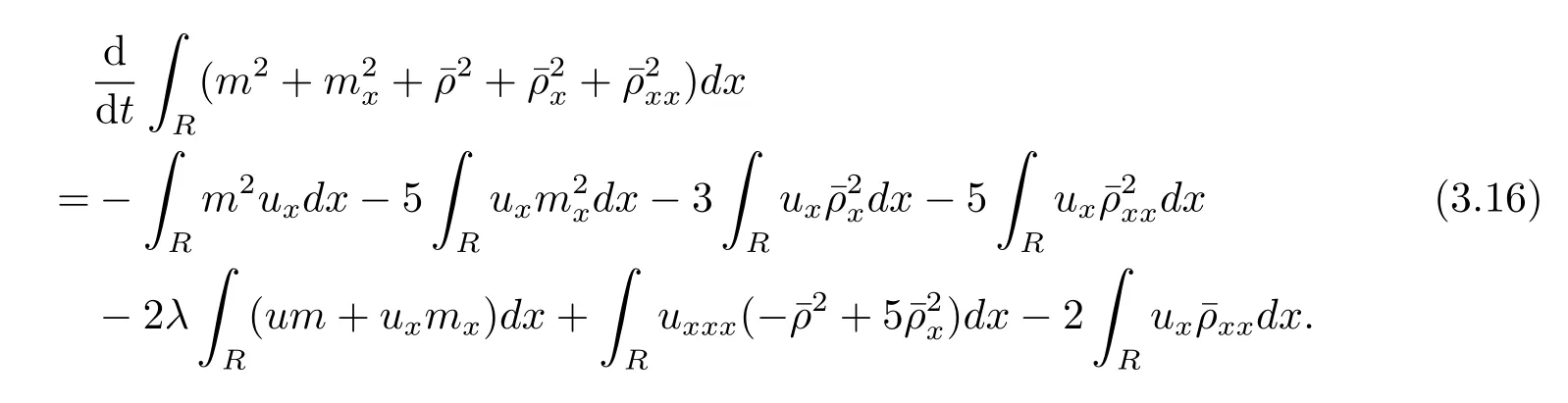
假设存在M1＞0,M2＞0,使得ux(t,x)≥-M1,∀(t,x)∈[0,T)×R,和M2,∀t∈[0,T).由引理3.5知有界,根据(3.16)式得到

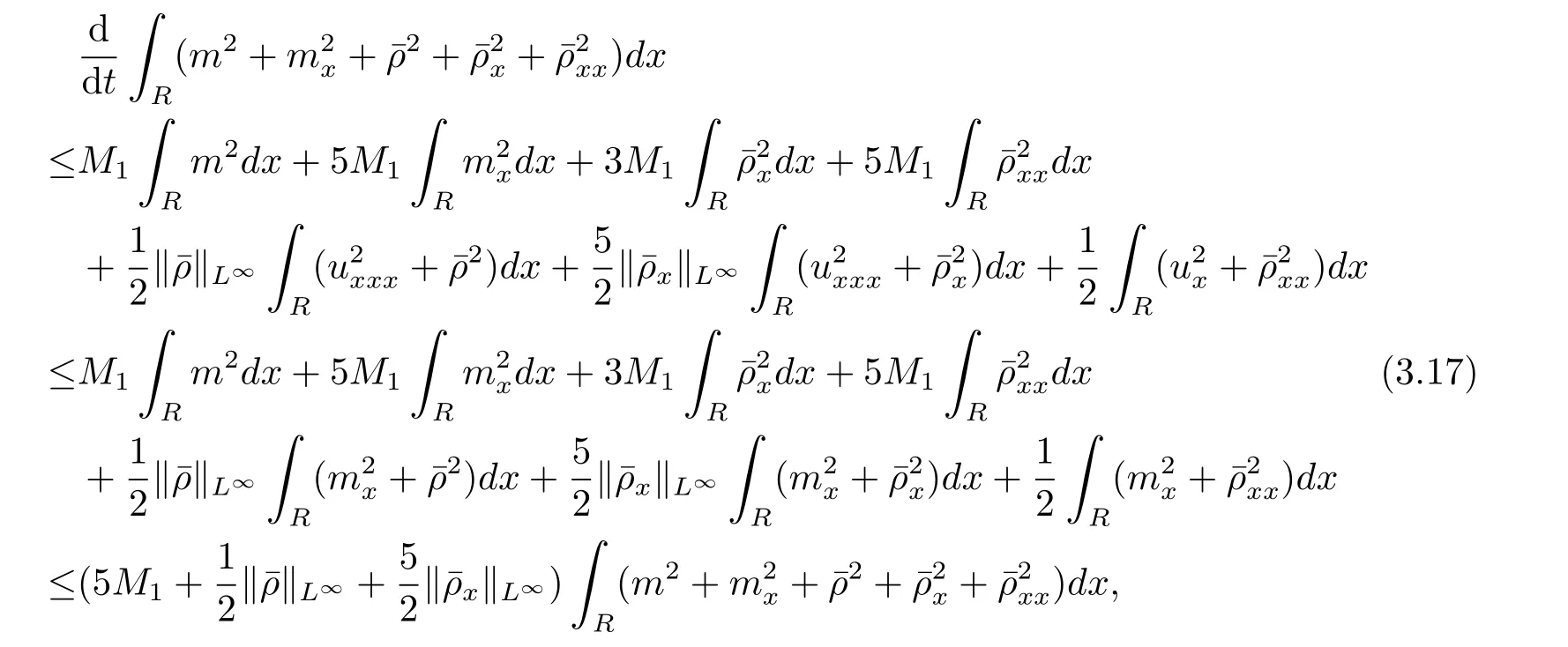
运用Gronwall不等式,得到∀t∈[0,T)有

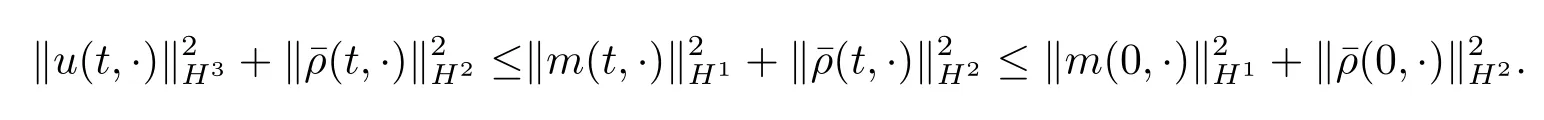
由上述不等式,Sobolev嵌入定理和推论3.1知解z在有限时间内不会爆破.

另一方面,由Sobolev嵌入定理知,若

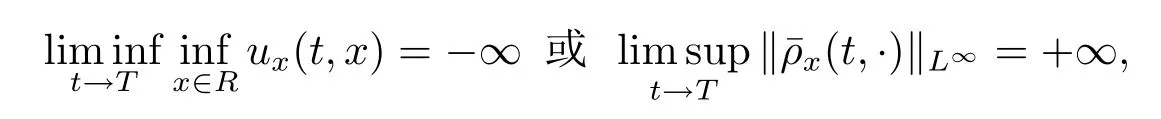
则解z就会在有限的时间内爆破.这就完成了对定理3.2的证明.

关于初始值z0∈H2×H1,有下述精确的爆破机制.

定理3.3设z0=∈H2×H1,且T是方程(2.3)关于初始值z0的解的最大存在时间,则方程(2.3)的H2×H1-解在有限时间内爆破当且仅当

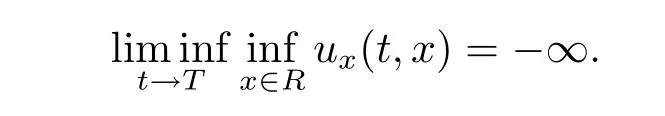
证根据定理2.2,设z=是方程(2.3)关于初始值z0∈H2×H1的解,且T是相应解z的最大存在时间,结合(3.10),(3.13)和(3.14)式,得到

假设存在M1＞0,使得∀(t,x)∈[0,T)×R,ux(t,x)≥-M1.根据(3.18)式得到

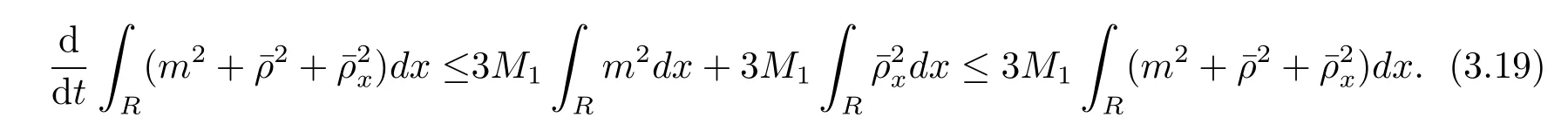
运用Gronwall不等式,得到∀t∈[0,T)有

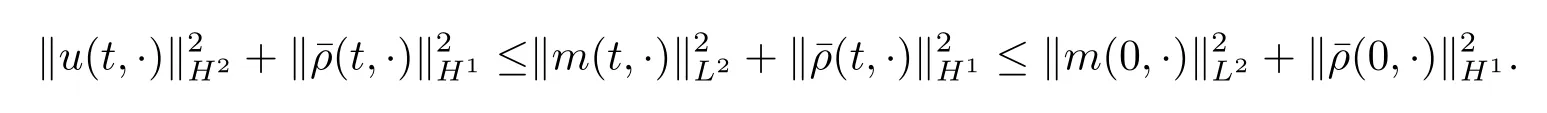
由上述不等式知,解z在有限时间内不会爆破.

注3.1由定理3.2得到

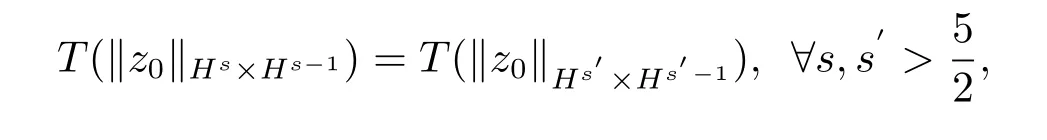
由定理3.3得到

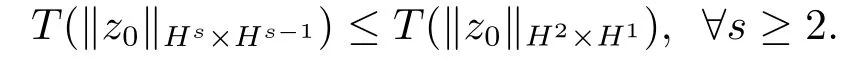
接下来,将讨论导致方程(2.2)解爆破的两个充分条件.

定理3.4设z0=∈Hs×Hs-1,s≥2,且T是方程(2.3)关于初始值z0的解的最大存在时间,若存在x0∈R,使得=-1,且

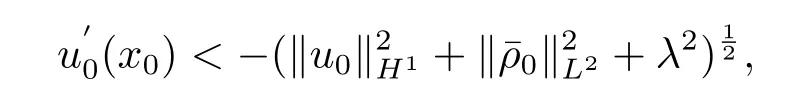
则方程(2.3)的解在有限时间内爆破.

证设z=是方程(2.3)关于初始值z0∈H2×H1的解,且T是相应解z的最大存在时间.令m(t)=ux(t,q(t,x0))和γ(t)=.由方程(2.3)和(3.8)式得到

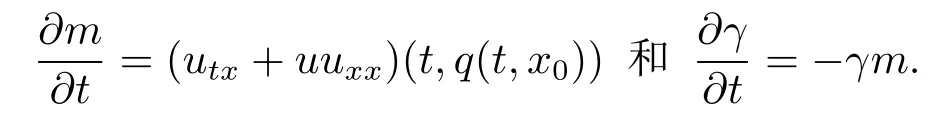
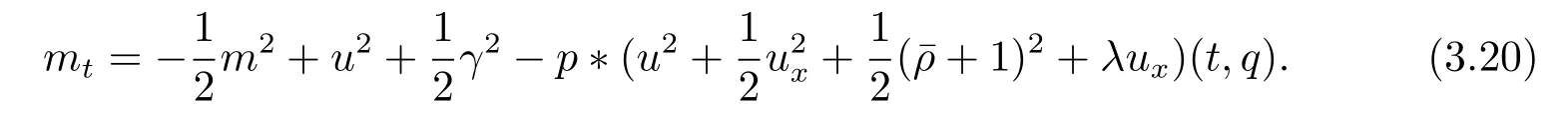
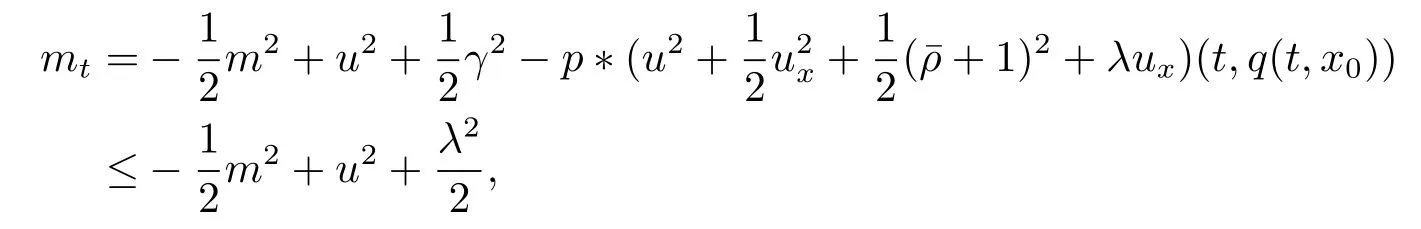
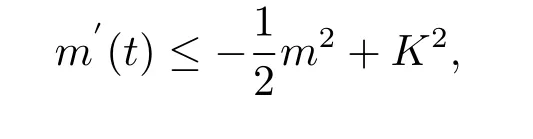
由定理3.2知解在有限时间内爆破.这就完成了对定理3.4的证明.

定理3.5设z0=∈Hs×Hs-1,s≥是方程(2.3)关于初始值z0的解的最大存在时间,,且存在M＞0,使得M,∀t∈[0,T).再假设存在x0∈R,使得

则方程的解在有限时间内爆破.

证由(3.3)式,可得

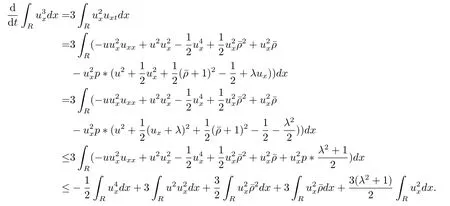
由引理3.3知

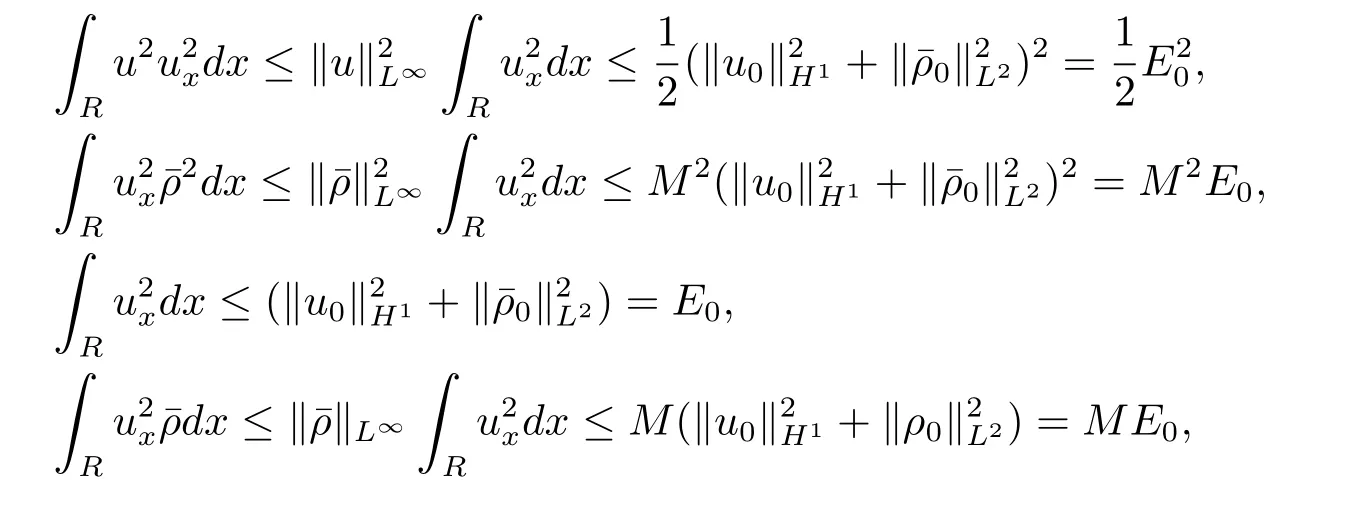
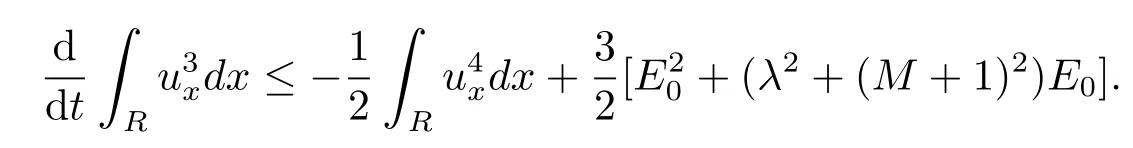
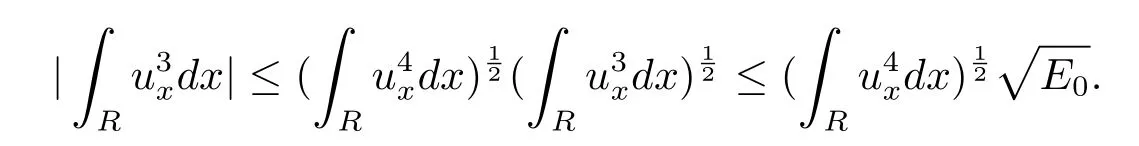
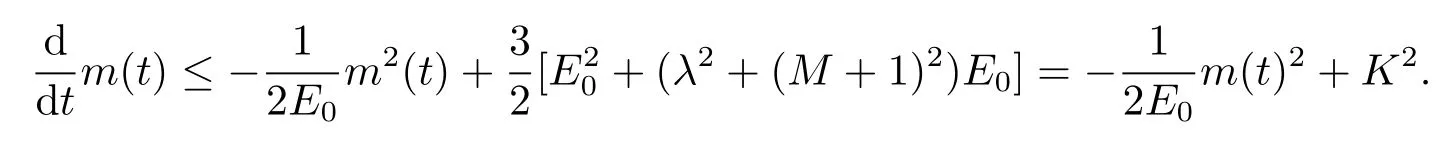
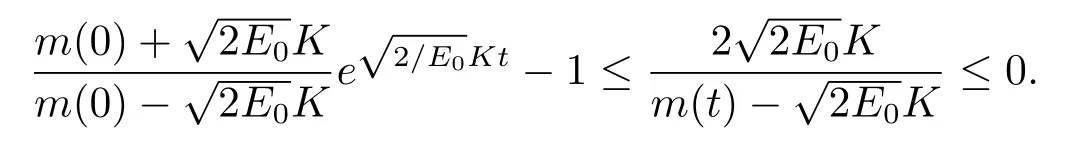
4 整体解

在这节中,将证明强解的整体存在性.首先先给出一个重要引理.

引理4.1设z0=∈Hs×Hs-1,s≥2,且T是方程(2.3)关于初始值z0的解的最大存在时间,若-1,∀x∈R,则存在β＞0,使得

证由引理3.4知q(t,·)是R上的一个递增微分同胚映射,满足

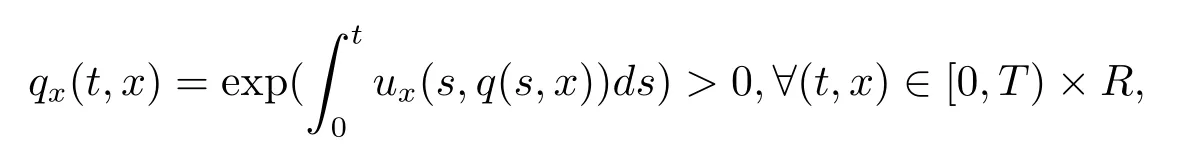
则有

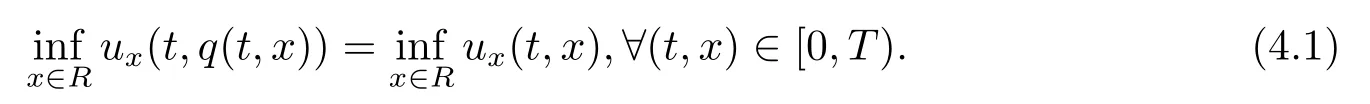
设M(t,x)=ux(t,q(t,x))和γ(t,x)=+1.由方程(2.3)和(3.8)式得

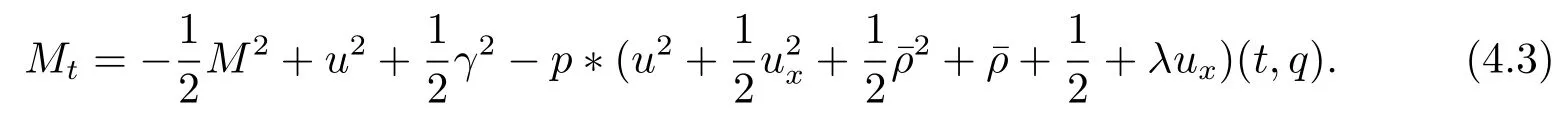
注意

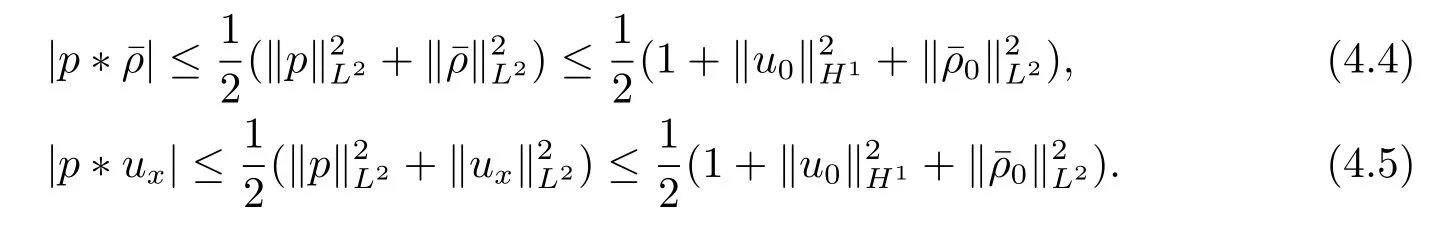
由引理3.3和(4.4)–(4.5)式,得到

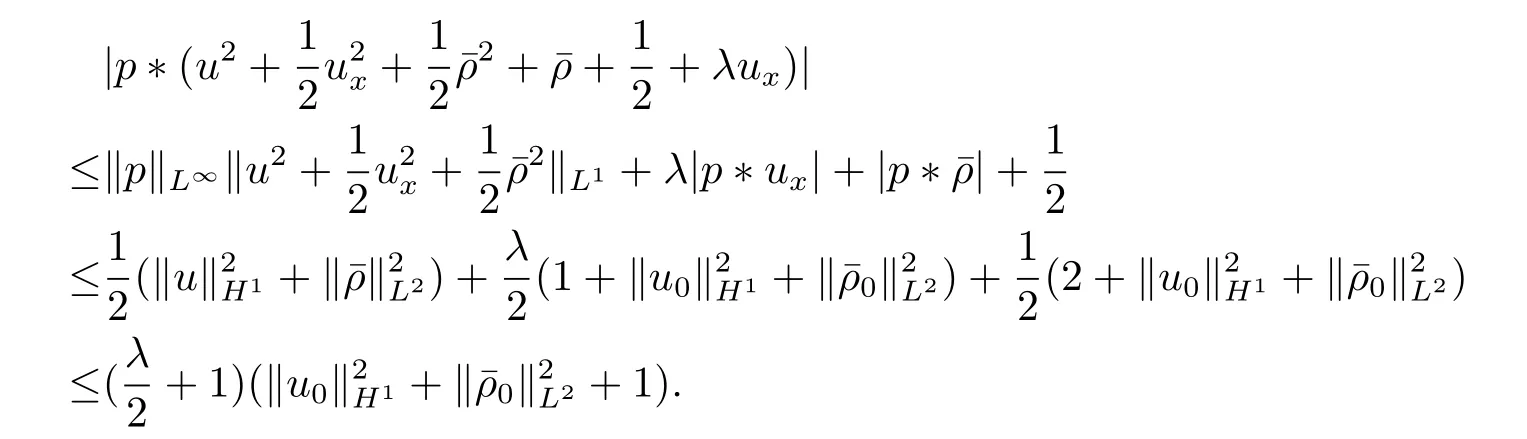
若设f(t,x)=u2(t,q)-λux)(t,q),则

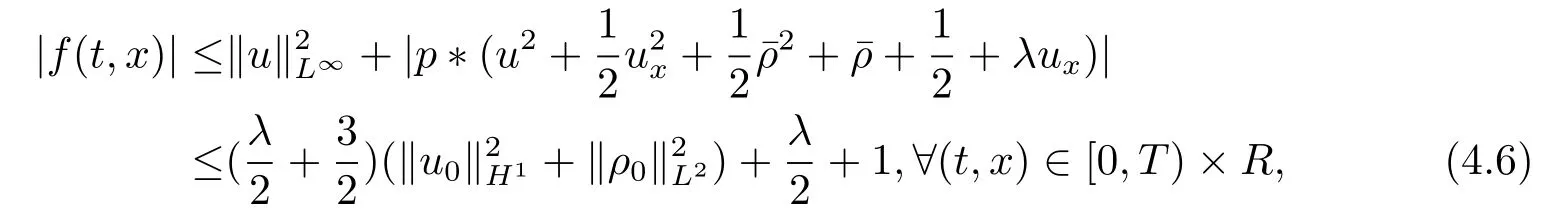
且

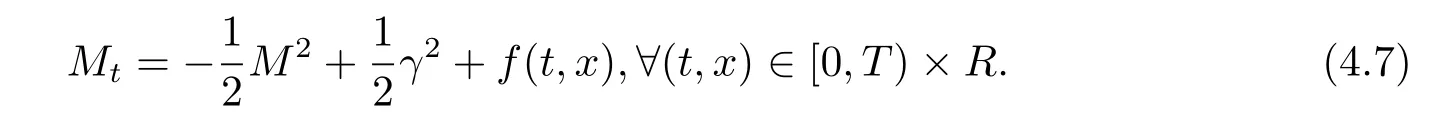
由引理3.4–3.5知∀x∈R,有γ(t,x)与γ(0,x)=ρ(0,x)同号.根据Sobolev嵌入定理,有且存在R0使得当|x|≥R0时,有因为-1,∀x∈R,则有

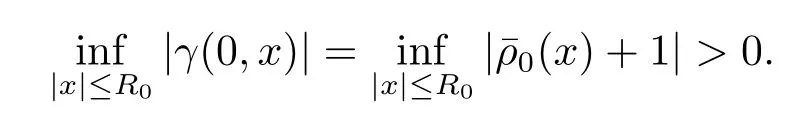
接下来考虑下述Lyapunov函数

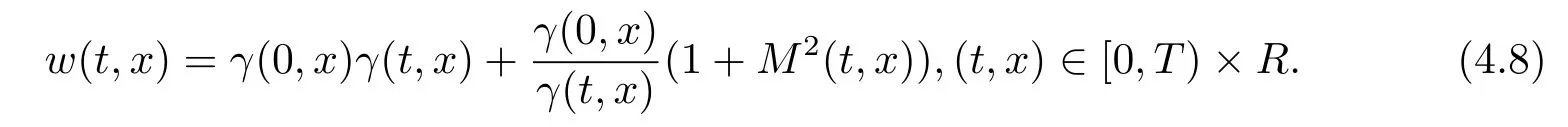
根据Sobolev嵌入定理知

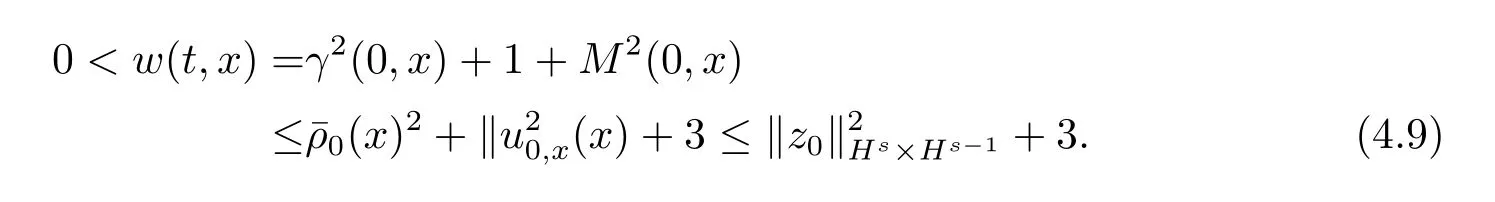
将(4.8)式关于t求偏导,再结合(4.2)式和(4.6)–(4.7)式,有

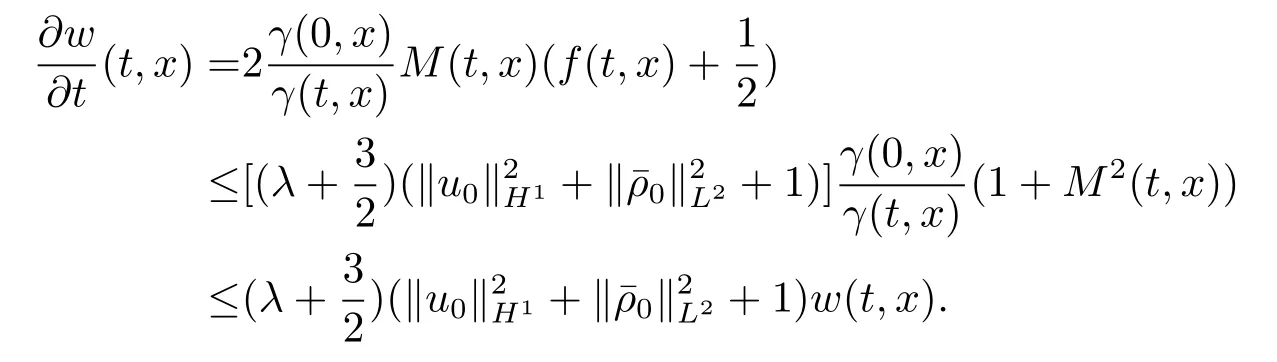
根据Gronwall不等式和上述不等式及(4.9)式,∀(t,x)∈[0,T)×R有

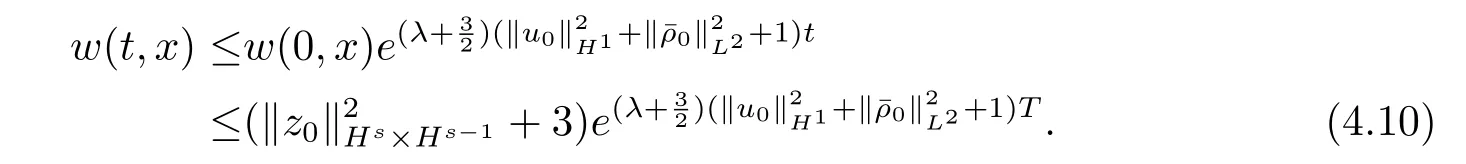
另一方面,

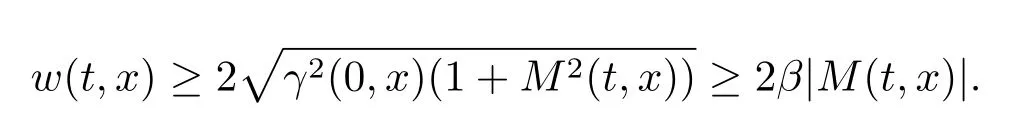
因此得到

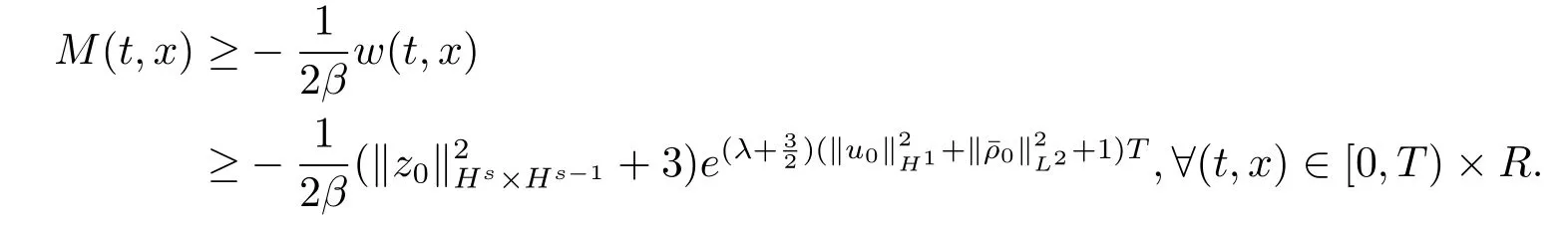
根据(4.1)式和上述不等式,得到

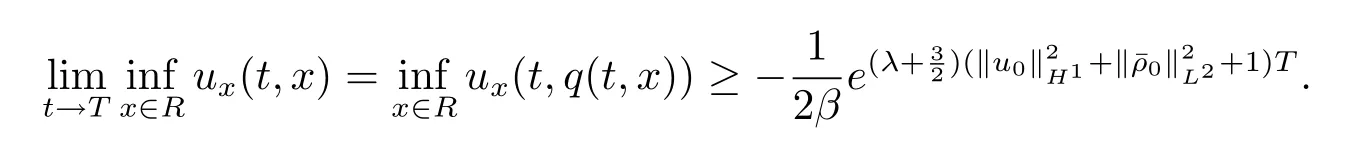
这就完成了对引理4.1的证明.

由定理3.2–3.3和引理4.1,可以直接得到以下两个定理.

定理4.1设z0=∈H2×H1,若-1,∀x∈R,则方程(2.3)的强解整体存在.

定理4.2设z0=若-1,∀x∈R,且T是方程关于初始值z0的解的最大存在时间,则方程(2.3)的解在有限时间内爆破当且仅当

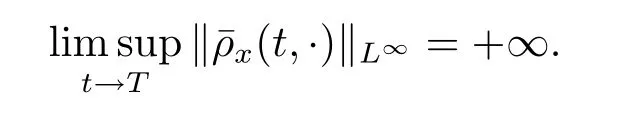
[1]Camassa R,Holm D D,Hyman J M.A new integrable shallow water equation[J].Adv.Appl.Mech., 1994,31:1–33.

[2]Fuchssteiner B,Fokas A S.Symplectic structures,their Bcklund transformations and hereditary symmetries[J].Physica D:Nonl.Phenomena,1981,4(1):47–66.

[3]Constantin A.On the scattering problem for the Camassa-Holm equation.Proceedings of the Royal Society of London[J].Series A:Math.,Phys.Engin.Sci.,2001,457:953–970.

[4]Constantin A,Escher J.Wave breaking for nonlinear nonlocal shallow water equations[J].Acta Math.,1998,181:229–243.

[5]Yin Z.Well-posedness,global existence and blow-up phenomena for an integrable shallow water equation[J].Discrete Contin.Dyn.Syst.,2004,10:393–411.

[6]C G,Yin Z.Global existence and blow-up phenomena for an integrable two-component Camassa-Holm shallow water system[J].J.Diff.Equ.,2010,248:2003–2014.

[7]Escher J,Lechtenfeld O,Yin Z.Well-posedness and blow-up phenomena for the 2-component Camassa-Holm equation[J].Discrete Contin.Dyn.Syst.A,2007,19:493–513.

[8]Constantin A,Ivanov R.On an integrable two-component Camassa-Holm shallow water system[J]. Phy.Lett.A,2008,372:7129–7132.

[9]Guan C,Yin Z.Global weak solutions for a two-component Camassa-Holm shallow water system[J]. J.Funct.Anal.,2011,260:1132–1154.

[10]Kato T.Quasi-linear equations of evolution,with applications to partial differential equations[J]. Lecture Notes Math.,1975,448:25–70.

[11]Curtain R,Zwart H.An introduction to infinite-dimensional linear systems theory[M].New York: Springer-Verlag,1995.

[12]Yin Z.On the Cauchy problem for an integrable equation with peakon solutions[J].Illinois J.Math., 2003,47:649–666.

[13]Kato T,Ponce G.Commutator estimates and Navier-stokes equatins[J].Comm.Oure Appl.Math., 1988,41:203–208.

[14]Liu J,Yin Z.On the Cauchy proplem of a periodic 2-componentµ-Hunter-Saxton system[J].Nonl. Anal.,2012,75:131–142.

[15]Beals R,Scattinger D,Szmigielski J.Acoustic scatting and extened Korteweg-de Vries hierarchy[J]. Adv.Math.,1998,140:190–206.

[16]徐能,李子宝.一类耗散型Camassa-Holm方程的解的爆破[J].数学杂志,2013,33(5):871–880.

GLOBAL EXISTENCE AND BLOW-UP PHENOMENA FOR THE TWO-COMPONENT CAMASSA-HOLM EQUATION WITH ZERO ORDER DISSIPATION

ZHU Shi-shi,ZANG Lin-en
(School of Mathematics,Yunnan Normal University,Kunming 650500,China)

In this paper,we study the two-component Camassa-Holm equation with the zero order dissipation.By using the Kato’s theorem,the local well-posedness is obtain.Then we study the global existence and blow-up phenomena of the solutions for the Cauchy problem.

two-component Camassa-Holm equation;zero order dissipation;local wellposedness;blow-up;global existence

tion:35G25;35L05

O175.29

A

0255-7797(2017)01-0152-17

2015-01-04接收日期:2014-10-27

国家自然科学基金资助(10961029).

朱师师(1989–),女,江西南昌,主要研究方向:偏微分方程.