启动压力影响下注采井间有效驱替规律

陈民锋，王兆琪，张琪琛，陈 璐

中国石油大学(北京)石油工程学院，北京 102249

【环境与能源 / Environment and Energy】

启动压力影响下注采井间有效驱替规律

陈民锋，王兆琪，张琪琛，陈 璐

中国石油大学(北京)石油工程学院，北京 102249

低渗透储层具有明显的启动压力梯度，导致注采井间的渗流场分布与常规条件存在一定差异．基于典型注采条件下的渗流特点和驱替过程分析，在产量方程中引入启动压力梯度，构建出考虑启动压力影响下一注一采定产渗流模型．通过推导得出注采井间压力场、速度场分布的数学表达式，并建立计算注采井间有效驱替面积、有效注采井距的方法，得到不同开发条件下井间渗流场分布和注采单元中有效驱替范围变化的规律．结合典型低渗透油藏参数进行的研究表明，根据有效驱替要求确定有效注采井距，并以此为基础部署开发井网，能在更大程度上有效驱动注采单元内的流体，进而提高低渗透油藏的开发效果．

油田开发；低渗透；启动压力梯度；渗流场；有效驱替；注采井距

与常规油藏相比，低渗透储层具有较为明显的启动压力梯度，在水驱开发过程中，流体在多孔介质中的渗流偏离达西定律，导致在注采井间部分区域内，若驱替压力梯度小于启动压力梯度，流体不能流动，直接影响了低渗透油藏储量的水驱动用效率[1-4]．

为保证注采井间的注采压差大于流体流动所需的启动压差，确定开发井距通常采用的方法是，在给定最大压差条件下，计算井间驱替压力梯度等于启动压力梯度时对应的极限注采井距．但这样确定的开发井距在实际生产中存在一定的问题，一方面，先利用势叠加原理求得压力分布，再减去启动压力梯度得到的计算公式，没有考虑启动压力梯度对渗流过程的影响，是一个等效处理手段；另一方面，在这种极限注采井距下建立的注采压差，只能使主流线附近区域内的流体能够流动(即注采连线的“线驱动”)，而整个注采单元大部分区域的流体由于受到的注采压差较小，而不能得到有效动用[5-12]．

启动压力梯度存在下的注采井间渗流场分布规律，与经典渗流理论得到的渗流场存在较大的差异，为了在注采井间有更多区域内的流体能够被驱替(即注采井间“面驱动”)，需要从基本渗流方程入手，研究在不同条件下注采井间压力场和速度场分布及变化规律．

本研究基于典型注采条件下的渗流特点和驱替过程分析，在产量方程中引入启动压力梯度，结合油井定产生产和注入井定量注入的条件，构建出无限大的地层中考虑启动压力影响的一注一采渗流模型，通过数学推导得出注采井间速度场和压力场分布的数学描述．基于典型注采条件下渗流场的分布特点，提出实现有效驱替的条件，通过研究注采单元中渗流场分布规律及驱替压力梯度与有效驱替范围的关系，建立确定低渗透油田水驱开发有效驱替注采井距的计算方法．

1 考虑启动压力下渗流方程及其解

1.1 基本注采渗流方程的建立

不同形式的注采井网，由于其注采井数比、井距、排距和位置等方面的不同，其注采井间的压力场、速度场分布规律不尽相同；但压力场是由各个单井(注入、采出)的势分布迭加、变换而成，而速度场是根据压力场分布进行相应的计算得到；因此，一注一采条件下的压力场、速度场就是典型的注采井间渗流场，是研究不同注采形式井网下注采井间渗流场的基础，反映了渗流场分布的最基本变化规律．因此，基于一注一采条件下的渗流问题，在基本渗流方程中引入启动压力梯度，结合油井定量生产和注入井定量注入的条件，构建出无限大地层中考虑启动压力影响的一注一采渗流模型，作为定量分析注采井间渗流场分布及变化规律的基础．

研究的目标油藏类型是孔隙型的低渗透砂岩油藏，在注水开采的过程中，渗吸现象(渗析驱替)及其作用很小，一般可以忽略，因此，在相应的注采渗流方程中，都省略渗吸项．

考虑启动压力梯度，渗流速度[13-15]应满足

(1)

其中， p为半径r处的地层压力； G为启动压力梯度； k为储层渗透率； μ为地层原油黏度．

设无限大地层中存在等产量的两口井， A点注水井产量为-q， B点生产井产量为q； 流体为单相不可压缩液体．见图1．

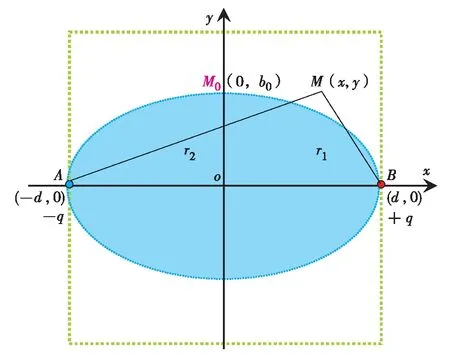
图1 一注一采对应关系示意图Fig.1 Schematic diagram of flooding unit

根据假设条件，则无限大地层等产量一注一采考虑启动压力时的基本微分方程[13-15]为

(2)

其边界条件为

(3)

其中，两井相距为2d； 井筒半径为rw； r1和r2分别为任意点M到注入井、生产井的距离；生产井井底流压为pwf； 注水井注入压力为pwi； h为储层有效厚度．

1.2 注采井间压力场、速度场分布的求解

将一注一采同时生产的问题，先分解为无限大地层一口生产井和一口注入井单独工作，然后再进行速度的“矢量”叠加．

无限大地层中一口生产井单独生产时，任一点流体的速度大小v生为

(4)

生产井引起在x方向上的分速度v生x为

(5)

同理，无限大地层中一口注入井单独生产时，任一点流体的速度v注为

(6)

注入井流体在x方向上的分速度v注x为

(7)

而式(7)中的井口产量q， 在考虑启动压力的情况下可表示为

(8)

将式(5)和式(7)两个解叠加，可得一注一采情况下地层任一点在x方向上的合速度为

(9)

令式(9)中y=0， 可得在注采主流线(x轴)上的速度分布表达式为

(10)

令式(9)中x=0， 可得在注采中间线(y轴)上的速度分布vx为

(11)

结合式(1)，对式(10)进行积分，可得主流线上压力分布的情况为

ln(d-x)]-Gx+C

(12)

利用注采井间中心点(x=0，y=0)处压力大小来确定式(12)的常数C

(13)

由此可得主流线上压力分布表达式为

(14)

同理，结合式(1)，对式(9)进行积分，可得一注一采条件下井间压力分布表达式为

(15)

结合式(4)和式(6)，通过矢量相加， v=v生+v注，可得一注一采条件下井间速度大小v分布为

(16)

1.3 注采单元中有效驱替范围的确定

在考虑启动压力梯度的影响时，注采井间压力场、速度场的分布规律，与经典渗流理论的结果存在一定差别．当给定注采压差和启动压力梯度等条件，在注采井中间线(y轴)上存在一点M0(x=0，y=b0)， 该点压力梯度等于启动压力梯度，则该点所处流线与对称流线(关于x轴对称)，所包含区域内的压力梯度均大于启动压力梯度，其中的流体都能够流动，称为可驱动区域．在图1中，方框内区域为注采井控单元，阴影区域为其中的可流动区域．

基于以上分析，可建立考虑启动压力影响、在不同生产条件下确定油藏注采单元进行有效驱替规律的步骤如下：

1.3.1 确定注采极限井距

① 已知储层启动压力梯度G和注采压差△p；

② 由式(10)，在注采主流线中心处(x=0)， 当速度值等于0时，可求得注采井间主流线上能够驱动(线驱动)的极限注采井距Dc；

③ 对于如图1的典型注采单元，图1中井控单元面积为SA=4bd； 在以下分析中，井控单元长度为2d， 宽度取值2b=2d．

1.3.2 确定井控单元中有效驱替区域范围

① 在极限注采井距内，取不同的井距进行计算分析，即取值0<2d≤Dc；

② 由式(10)，可先得出此时主流线中心处(x=0)的速度vm；

③ 在可动区域内，不同位置流动速度差别较大，为保证有效开发，要求可动边界上的速度大于0．由式(11)，当其值等于θ×vm时(θ为外流动边界速度的倍数， 0<θ≤1)， 可得到相应条件下注采单元中能够有效驱替的边界be； 则相应包含的区域，即为井控单元中的有效驱替区域．

1.3.3 确定井控单元中有效驱替面积系数

① 当边界流速不为0时，其边界包含的面积即为注采井控单元中有效驱替面积．结合式(16)，有效驱替面积可表达为

(17)

② 注采井控单元有效驱替面积系数为

(18)

一般0<ωe≤1． 有效驱替面积系数ωe越大，说明在井控单元中，得到有效驱替的范围越大．

对于给定的油藏条件和生产条件，可以作出不同注采压差、启动压力梯度下，可驱动面积系数、有效驱替面积系数与注采井距的关系，为实际油藏开发井网的部署，提供技术支持．

2 注采井间渗流场变化规律

2.1 注采单元中压力场、速度场分布规律

利用建立的方法进行相关理论研究．基本参数为：井半径为0.1 m，注采井距变化为±200 m；启动压力梯度取值范围为0～0.05 MPa/m，注采压差△p取值范围为5～20 MPa．

基于式(15)和式(16)，得到一注一采情况下，分别考虑有无启动压力梯度时的压力场、速度场分布，见图2和图3．

图2 一注一采对应条件下井间压力场分布Fig.2 Pressure field distribution of flooding unit

图3 一注一采对应条件下井间速度场分布Fig.3 Velocity field distribution of flooding unit

由图2和图3可见，由于启动压力梯度直接影响着流体的渗流过程，因此，有无启动压力梯度时的压力场分布存在一定的差别．在无启动压力梯度时(G=0)的压力场，与经典渗流理论结果相同， y轴线是等压线， x轴是流线，整个水动力学场关于y轴对称．在存在启动压力梯度时(G≠0)的压力场，在相同的注采压差下，由于井间的压力消耗增加，使得等压线的分布形态出现较大变化，等压线在注采井间的变化幅度大、变化频率快；而速度场也关于x轴和y轴对称，但流速大于0的范围明显变小．

2.2 注采井间有效驱替变化规律

对于不同启动压力梯度和注采压差条件，首先计算出相应的极限注采井距，再确定有效驱替面积系数的变化规律．根据式(10)计算不同条件下极限注采井距，结果见图4．

由图4可见，随着启动压力梯度的增大，极限注采井距呈幂函数逐渐减小；极限井距是注采井网部署时的最大限制井距，在相同的启动压力梯度条件下，增大注采压差可以在一定程度上增大极限注采井距．

图4 不同条件下极限注采井距变化曲线Fig.4 Variation curves of limit injector producer distance under different conditions

取启动压力梯度G为0.01～0.05 MPa/m、注采压差△p为5～20 MPa，有效驱替面积系数与注采井距的变化关系，结果见图5．

图5 有效驱替面积系数变化曲线Fig.5 Variation curves of effective displacement area coefficient

由图5可见，在极限井距内，随着注采井距的减小，有效驱替面积系数逐渐增大；注采压差越大、启动压力梯度越小，井控单元内有效流动区域的面积越大．

在实际开发中，希望在注采井控单元中能够有效流动的区域越大越好，一般有效驱替面积系数ωe>0.5， 此时其对应的开发井距可称为有效注采井距．可以得出不同启动压力梯度、不同注采压差下，有效注采井距的变化如图6．

图6 不同条件下有效注采井距变化曲线Fig.6 Variation curves of effective injector producer distance under different conditions

由图6可见，随着启动压力梯度的增大，油藏有效注采井距逐渐减小；而随着注采压差的增大，有效注采井距逐渐增大．

设系数λ为有效注采井距与极限注采井距的比值，其值大小与启动压力梯度和生产压差呈非线性关系．对比图4和图6，在相同启动压力梯度G下，系数λ随注采压差△p的增大而增大．

系数λ与启动压力梯度G和注采压差△p的变化关系，可表示为

λ=0.533 4+e(-2.108+11.72G+0.0125 7△p)

(19)

在G为0.01～0.05 MPa/m、 △p为5～20 MPa时，有效注采井距与极限注采井距的比值约在0.7～0.8．由于极限注采井距的计算相对简单，在实际操作中可先求出油藏的极限注采井距，然后利用关系式(19)求出λ， 进而得到对应的有效注采井距，以此来指导低渗透油藏的开发部署．

3 结 论

综上研究可知：

1)考虑启动压力梯度后，使注采井间渗流阻力增加，导致注采井间的压力场、速度场分布规律发生明显变化．

2)启动压力梯度对水驱开发的影响，主要体现在增加渗流阻力、降低流体在介质中的流动能力，使得水驱有效动用的范围明显减小；为满足注采单元有效驱替范围的要求，有效注采井距一般都小于其极限注采井距，两者的比值与启动压力梯度和生产压差呈非线性关系．

3)本研究基于典型注采条件下渗流场的分布特点，提出实现有效驱替的要求，进而建立了计算低渗透水驱开发有效注采井距的方法；计算分析表明，本方法具有很好的操作性，可以指导此类油藏注采井距的合理部署．

/ References：

[1] 陈民锋,赵 晶,张贤松,等. 低渗透稠油油藏水平井极限动用范围[J]. 中国石油大学学报自然科学版,2014, 38(2):103-108. Chen Minfeng, Zhao Jing, Zhang Xiansong, et al. Limit drainage radius of horizontal wells in low-permeability heavy oil reservoirs[J]. Journal of China University of Petroleum Natural Science Edition, 2014, 38(2):103-108.(in Chinese)

[2] 冯其红，王守磊，韩晓冬，等. 考虑启动压力的层状油藏开发指标计算方法[J]. 西南石油大学学报自然科学版, 2015, 37(2): 87-92. Feng Qihong, Wang Shoulei, Han Xiaodong, et al. Calculation method of development indexes for multilayered reservoir with starting pressure included[J]. Journal of Southwest Petroleum University Science & Technology Edition，2015, 37(2): 87-92.(in Chinese)

[3] 高苗苗，安 山，王 鹏. 引入启动压力梯度计算低渗储层合理注采井距[J].辽宁化工，2010，39(12)：1276-1278. Gao Miaomiao, An Shan, Wang Peng. Calculation of permeability reservoir rational injection-production well spacing by introducing start-up pressure gradient[J]. Liaoning Chemical Industry， 2010，39(12)：1276-1278.(in Chinese)

[4] 陈民锋，赵 晶，赵梦盼，等. 低渗透稠油油藏储量有效动用界限研究[J]. 深圳大学学报理工版. 2013，30(2)：210-215. Chen Minfeng, Zhao Jing, Zhao Mengpan, et al. Study on limits of effective drive in low-permeability heavy-oil reservoirs[J]. Journal of Shenzhen University Science and Engineering. 2013，30(2)：210-215.(in Chinese)

[5] 李忠兴，韩洪宝，程林松，等. 特低渗油藏启动压力梯度新的求解方法及应用[J].石油勘探与开发, 2004，31(3)：107-109. Li Zhongxing, Han Hongbao, Chen Linsong, et al. A new solution and application of starting pressure gradient in ultra-low permeability reservoir[J]. Petroleum Exploration and Development， 2004，31(3)：107-109.(in Chinese)

[6] 姚 猛，雷 刚，胡 嘉. 考虑启动压力梯度的面积井网极限井距计算[J].科学技术与工程，2013，13(25)：7316-7320. Yao Meng, Lei Gang, Hu Jia. Calculating the limit well spacing of area well pattern considering threshold pressure gradient[J]. Science Technology and Engineering， 2013，13(25)：7316-7320.(in Chinese)

[7] 王熙华. 利用启动压力梯度计算低渗油藏最大注采井距[J].断块油气田，2003，10(6)：75-76. Wang Xihua. Using start-up pressure gradient to calculate low-permeability reservoir’s biggest producer-injector spacing[J]. Fault-Block Oil & Gas Field，2003，10(6)：75-76.(in Chinese)

[8] 陈民锋，陈 璐，张琪琛，等. 低渗透油藏改造后水平井压力分布规律[J]. 深圳大学学报理工版. 2016，33(4)：401-408. Chen Minfeng，Chen Lu，Zhang Qichen，et al. Field pressure distribution of horizontal wells in low permeable stimulated reservoirs[J]. Journal of Shenzhen University Science and Engineering.，2016，33(4)：401-408.(in Chinese)

[9] 谷维成，莫小国，朱学谦，等. 文留油田低渗透油藏合理注采井距研究[J].油气地质与采收率，2004，11(5)：54-56. Gu Weicheng, Mo Xiaoguo, Zhu Xueqian, et al. Research on reasonable injection-production well spacing in Wenliu oil reservoir with low permeability[J]. Petroleum Geology and Recovery Efficiency， 2004，11(5)：54-56.(in Chinese)

[10] 王端平，时佃海，李相远，等. 低渗透砂岩油藏开发主要矛盾机理及合理井距分析[J].石油勘探与开发，2003，30(1)：87-89. Wang Duanping, Shi Dianhai, Li Xiangyuan, et al. Main challenges and the reasonable well spacing for the development of low-permeability sandstone reservoirs[J]. Petroleum Exploration and Development， 2003，30(1)：87-89.(in Chinese)

[11] 孔嫦娥，胡 嘉，姚 猛. 考虑启动压力梯度计算直井——水平井联合布井时注采极限井距[J].辽宁化工，2013，42(11)：1334-1337. Kong Chang’e, Hu Jia, Yao Meng. Calculation of the critical well spacing in combination well pattern of horizontal and vertical wells considering start-up pressure gradient[J]. Liaoning Chemical Industry， 2013，42(11)：1334-1337.(in Chinese)

[12] 唐伏平，唐 海，余贝贝，等. 存在启动压力梯度时的合理注采井距确定[J].西南石油大学学报自然科学版，2007，29(4)：89-91. Tang Fuping, Tang Hai, Yu Beibei, et al. The determination of the injection-production well spacing with the consideration of the start-up pressure gradient[J]. Journal of Southwest Petroleum University Science & Technology Edition， 2007，29(4)：89-91.(in Chinese)

[13] 王建俊，鞠斌山，罗二辉. 低速非达西渗流动边界移动规律[J]. 东北石油大学学报，2016，40(2)：71-77. Wang Jianjun, Ju Binshan, Luo Erhui. Movement characteristics of moving boundary in non-Darcy flow with low velocity[J]. Journal of Northeast Petroleum University，2016，40(2)：71-77.(in Chinese)

[14] 张建国. 油气层渗流力学[M].东营：石油大学出版社，1998. Zhang Jianguo. Oil and gas percolation mechanics[M].Dongying: Petroleum University Press，1998.(in Chinese)

[15] 李道品. 低渗透砂岩油田开发[M].北京：石油工业出版社，1997. Li Daopin. Low permeable sandstone oilfield development[M].Beijing: Petroleum Industry Press，1997.(in Chinese)

[16] 李晓平. 地下油气渗流力学[M].北京：石油工业出版社，2008：68-71. Li Xiaoping. The underground oil and gas percolation mechanics[M].Beijing: Petroleum Industry Press，2008：68-71.(in Chinese)

【中文责编：晨 兮；英文责编：天 澜】

Effective displacement rules for interwell with threshold pressure

Chen Minfeng†, Wang Zhaoqi, Zhang Qichen, and Chen Lu

College Petroleum Engineering, China University of Petroleum (Beijing), Beijing 102249, P.R.China

Due to the existence of significant threshold pressure gradient, the flow in low permeability reservoirs is low-speed non-Darcy flow. Under these conditions, interwell flow filed has significant difference compared to the fields of conventional reservoirs. In view of the flow characteristics and displacement process analysis of a typical water flooding regime, threshold pressure gradient is introduced into the basic flow equation and combined with the condition that both production and injection wells are working in a constant rate. A mathematical model is established for one injector producer pair in infinite formation. According to the initial and boundary conditions, interwell pressure and velocity field distribution function are deduced from the model. Based on the mathematical description, interwell pressure and velocity field distribution and variation could be defined. The analysis shows that for the waterflood development of low permeability oilfield, only by taking effective flooding strategy, can the oil between the injection and production wells be effectively displaced to a greater extent and can the development effectiveness of low permeability reservoirs be improved.

oilfield development; low permeability reservoirs; threshold pressure gradient; pressure and velocity field; effective producing area; injector producer distance

Received：2016-03-28；Revised：2016-10-10；Accepted：2016-10-30

Foundation：National Basic Research Program of China (2015CB250905)

† Corresponding author：Associate professor Chen Minfeng. E-mail: cmfllp96@126.com

：Chen Minfeng, Wang Zhaoqi, Zhang Qichen, et al. Effective displacement rules for interwell with threshold pressure[J]. Journal of Shenzhen University Science and Engineering, 2017, 34(1): 91-97.(in Chinese)

TE 345

A

10.3724/SP.J.1249.2017.01091

国家重点基础研究发展计划资助项目(2015CB250905)

陈民锋(1971―)，男，中国石油大学(北京)副教授、博士. 研究方向：油气田开发系统理论方法和提高采收率. E-mail：cmfllp96@126.com

引 文：陈民锋，王兆琪，张琪琛，等. 启动压力影响下注采井间有效驱替规律[J]. 深圳大学学报理工版，2017，34(1)：91-97.