颗粒堆积模型在混凝土中的应用

龙武剑，周 波，梁沛坚，孙柔嘉

深圳大学土木工程学院，广东省滨海土木工程耐久性重点实验室，广东深圳 518060

【土木建筑工程 / Architecture and Civil Engineering】

颗粒堆积模型在混凝土中的应用

龙武剑，周 波，梁沛坚，孙柔嘉

深圳大学土木工程学院，广东省滨海土木工程耐久性重点实验室，广东深圳 518060

评述颗粒堆积模型的基本理论、发展及其最新应用. 对比分析多种颗粒堆积模型间的差异，指出颗粒堆积模型的主要优点、局限性及其在复合颗粒体系材料领域中的应用范围. 分析表明，利用颗粒堆积模型优化计算混凝土的堆积密实度，可以降低复合颗粒体系间的空隙体积，使颗粒系统达到最紧密堆积状态，减少混凝土中胶凝材料的用量，实现低胶凝材料用量绿色混凝土优化设计.

混凝土；颗粒堆积模型；堆积密实度；颗粒体系；松动效应；附壁效应；空隙率；配合比

近年来，绿色生态混凝土的研究及制备在新型建筑材料研发领域备受关注. 混凝土作为应用最广泛且用量最大的建筑材料，虽然给人类提供了很大的便利性，但其生产制备过程也给环境带来极大的负面影响. Gao等[1]研究发现，全球仅水泥产业每年就产生约1.8 ×1011kg的二氧化碳排放量，占世界二氧化碳总排量的7%左右，导致了生态环境被严重破坏.

实现绿色生态混凝土的制备及生产途径有许多，其中之一是通过降低水泥用量，达到减少能源消耗，降低二氧化碳排放量的目的[2-5]. 从宏观而言，混凝土混合料可被认为是由不同尺寸颗粒堆积而成的颗粒系统，并被胶凝材料水化产物包裹胶结而成的一个整体. 因此，基于颗粒堆积模型可以优化混凝土混合料级配，使混凝土混合物尽可能达到最密实状态，从而将颗粒间的空隙率达到最低；同时，在保持原水胶比不变的前提下，通过减少填充空隙之间的用水量，最终降低其水泥用量，达到环保的目的.

本研究评述了颗粒堆积模型的基本理论和应用研究，旨在为绿色混凝土材料设计奠定基础. 目前颗粒堆积模型的应用技术仍处于实验阶段，尚未形成完善的适用于混凝土材料设计的应用理论. 系统研究颗粒堆积模型在绿色生态混凝土中的应用理论及设计方法，有利于低水泥用量绿色混凝土在建材行业中的健康、可持续发展.

1 颗粒堆积理论

颗粒有宏观和微观之分. 从宏观角度来看，它可以指砂、石、土，甚至是大的混凝土试件等；从微观角度而言，它指的是分子和原子等. 同时，颗粒根据本身的不同特征可有不同的分类形式，例如，根据表观形态，可以分为规则形态(球体和立方体等)和不规则形态；根据堆积方式，可分为有序堆积和随机堆积(在重力影响下的一种随机堆积方式). 对于宏观颗粒的堆积，一般指在自身重力作用下的一种堆积方式. 微观颗粒的堆积影响因素相对较为复杂，因还需考虑静电作用和范德华力.

由于颗粒本身形貌及组成的复杂性，近一个世纪以来颗粒堆积问题一直是数学家、化学家、材料科学家及其他相关行业领域专家持续关注的焦点之一. 颗粒堆积理论主要是在20世纪30年代提出，可分为连续分布的颗粒体和不连续分布的颗粒体. 连续分布的颗粒体由某一粒级范围内所有尺寸颗粒组成，不连续分布颗粒体则由该粒级范围的有限尺寸颗粒所组成.

Westman等[6]提出了的颗粒堆积理论及计算多元颗粒最大堆积率的方法，表观体积为

(1)

其中， Va为单位实际体积颗粒的表观体积； ε为单位实际体积空隙所占的空隙率； ω为单位实际体积颗粒所占的容积率.

Westman等[6]认为当粗细颗粒尺寸的比值达到某一个非常大的值时，可得出以下结论：① 当单一容积内粗颗粒所占组成部分接近100%时，粗细颗粒混合料的表观体积主要由粗颗粒决定，而细颗粒填入粗颗粒之间的空隙，可以忽略其所占容积；② 当单一容积内细颗粒所占组成部分接近100%时，细颗粒形成气孔并环绕粗颗粒堆积，这时混合料的表观体积除包括细颗粒的表观体积之外，还包含粗颗粒的实际体积.

Andreason[7]认为，用同一粒径颗粒混合物的堆积理论不能准确计算实际颗粒混合物的堆积率. 因此，他将颗粒的实际分布描述为具有同样形式的分布，即“统计类似”，并提出了Andreason方程：

(2)

其中， Y(D)为小于粒径D的累计筛余百分数； D为颗粒粒径； Dmax为颗粒体中最大颗粒粒径； n为模型分布指数.

式(2)描述了包含无限小的尺寸颗粒，这种情况虽然在实际的颗粒体系中不可能存在，但是Andreason[7]认为，假如对于颗粒系统中最小颗粒的尺寸是有限小的或者是无限小的，则通过该方程计算出来的结果与实际值并没有很大的差别. Andreason还通过实验结果得出了另一个结论，即对于颗粒各种分布的气孔率随着该方程中的颗粒分布指数n而减少，并认为若使颗粒实际分布的气孔率达到最小值， n的适宜取值范围为0.33～0.50.

上述颗粒堆积的经典理论，虽然存在一些不足，但对颗粒堆积模型的系统研究具有深远的理论影响和实用意义，如基于经典堆积理论Andreason方程基础而修正所得的Dinger-Funk方程[8]等.

2 颗粒堆积模型的研究现状

2.1 颗粒堆积模型的发展

颗粒堆积模型是以数学方程为基础，用来描述不同大小颗粒之间的几何作用方式. 用模型来计算混凝土混合物的理论堆积密实度，是基于颗粒级配和颗粒群组的堆积密实度，且几乎所有的颗粒堆积模型的数学方程本构是一致的.

早在20世纪30年代，Furnas[9]首次用数学方程来描述颗粒堆积模型，提出了Furnas模型，但最初的Furnas模型是基于球形颗粒堆积理论，且只有在不考虑两个粒径颗粒间作用的前提下才能应用该模型，即当大颗粒占主导时，小颗粒能够填充在大颗粒之间的空隙中，或以小颗粒为主时，大颗粒镶嵌在小颗粒基体中. 然而，这与颗粒的实际堆积情况有较大差别. 在随后的几十年里，大量研究者基于Furnas理论和试验研究，对颗粒堆积模型进行不断的改善，提出了不同的颗粒堆积模型. 在这些模型中涉及到两种效应，即松动效应和附壁效应[9]. 松动效应是指在以粗颗粒为主的情况下，细颗粒填充在粗颗粒堆积的空隙之中，并与空隙大小相比足够大，如图1；附壁效应是指在以细颗粒为主的情况下，某些单个粗颗粒处于细颗粒群之中，而环绕粗颗粒接触界面堆积的细颗粒会出现一些空隙量，如图2. 这两种效应都随着颗粒粒径比值的增大而逐渐提高，但这两种效应的最大值均为1，即两种颗粒材料粒径相等且完全相互作用的情况(完全相互作用指的是某一尺寸颗粒的排列会受到邻近的另一不同尺寸颗粒的影响).

图1 松动效应[9]Fig.1 Loosening effect[9]

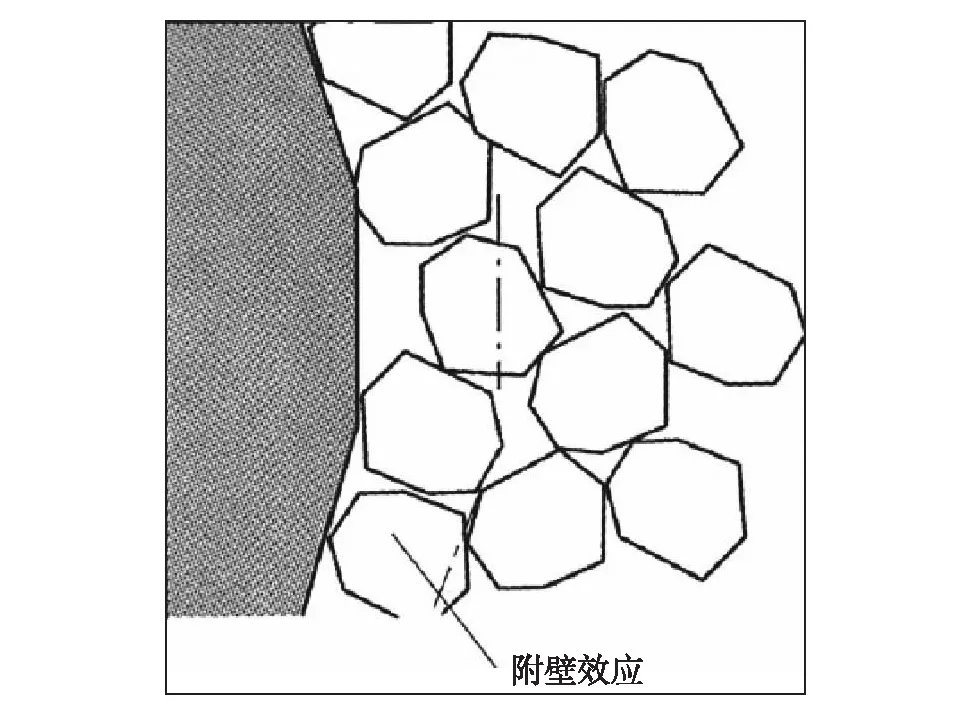
图2 附壁效应[9]Fig.2 Wall effect[9]

1977年，Toufar等[10]提出了Toufar模型，并用该模型来预测直径比在0.22～1.00的二元混合料的堆积密实度，它与Aïm 等[11]在1968年提出的模型相同之处在于前者只考虑了二元混合料颗粒之间的附壁效应，而忽视了颗粒间的松动效应. 1997年，Goltermann等[12]对Toufar模型进行了修正，除了考虑颗粒之间的附壁效应外，还包含了松动效应. 修正的Toufar模型对二元混合料堆积密实度的预测也较准确，但是当混合料中颗粒级别被划分较多时，其预测堆积密实度的准确性将会降低，甚至会出现较大的偏差[13].

1986年，Stovall等[14]通过将粉末颗粒堆积体系分为挤塞和非挤塞体系，提出了线性堆积密实度模型(linear packing density model，LPDM). 应用该模型的条件是：假设在粉末颗粒堆积过程中，不考虑颗粒之间的静电作用、范德华分子作用及颗粒团聚作用等因素的影响，仅考虑颗粒间几何作用对颗粒堆积密实度的影响. 此模型虽是现有粉末颗粒堆积模型中预测堆积密实度准确度较高的模型，但由于其没有考虑到替换机制[15]，即当二元颗粒的粒度比大于某一临界值时，其他颗粒的加入量对其堆积密实度无影响，故该模型的精度仍有待提高.

1998年提出的Dewar模型[16]通过利用正方形形状颗粒的堆积方式来推导颗粒间的相互作用，这在一定程度上间接地考虑了颗粒的形状和纹理. 由于该模型采用的是逐步回归算法，且在模型中引入了两个系数，黏性调整系数和经验调整系数，从而局限了模型向颗粒形状或者颗粒表面力作用效应两个方面去发展.

1999年，Larrard[17]提出了线性堆积密实度模型和可压缩堆积模型(compressible packing model，CPM)，这两种模型都需测量混凝土混合料的颗粒级配曲线. 线性堆积密实度模型是对Furnas模型的拓展和改进，既可以预测多元混合料的堆积密实度，又考虑了混合料颗粒之间的几何作用(附壁效应和松动效应). 而可压缩堆积模型是基于线性堆积密实度模型和固体悬浮模型(solid suspension model, SSM)发展而成，它不仅考虑了混合料中不同尺寸颗粒间的相互作用，且涵盖了混合料不同堆积形式对颗粒堆积密实度的影响，甚至通过大量实验对颗粒压实指数K进行了校正，并给出了K在不同堆积形式下的取值，如表1. 因此，CPM模型对预测任意分布及任意量的骨料颗粒组合而成的混合料堆积密实度具有较高的准确度，并得到大多数研究者的认可且被广泛应用.

表1 不同堆积形式下K的取值[17]

Kwan等[18-20]通过对颗粒堆积模型进行进一步研究，在原颗粒结构堆积效应(附壁效应和松动效应)的基础上，再引入了一个新的几何作用效应——楔入效应，该效应存在如图3和图4两种情况. 图3表明了当混合料中组成部分主要是粗颗粒时，细颗粒不能填充在粗颗粒自身堆积之间的空隙，而是处于粗颗粒与粗颗粒之间，即将两个相邻的粗颗粒分离开；图4表明了当混合料中细颗粒占主要成分时，细颗粒环绕少量粗颗粒堆积，同样使得两个可以相接触的粗颗粒分离. Kwan根据这3种效应建立了三参数模型，并利用该模型对同一形状(椭圆或菱角状)颗粒混合物的堆积密实度进行预测．结果表明，该三参数模型不但突破了线性堆积理论的局限性，同时具有较高的预测准确度.

图3 粗骨料占主导地位的楔入效应[18]Fig.3 The wedging effect when the coarse particles are dominant[18]

图4 细骨料占主导地位的楔入效应[18]Fig.4 The wedging effect when the fine particles are dominant[18]

Knop等[21]基于Stovall和Larrard提出的线性堆积密实模型，对其部分进行了简单修正，并利用修正模型对水泥与不同尺寸的石粉颗粒任意混合组合的堆积密实度进行预测．结果表明，其值与实际值的误差在允许范围之内.

2.2 离散单元法在颗粒体系中的应用

近年来，随着计算机技术的不断发展，许多研究者已利用相应的数学工具对颗粒体系在不同形式下的堆积过程进行了模拟；尤其是离散单元法(discrete element model, DEM)在颗粒体系中的应用已得到广大研究者的认可.

利用离散单元法进行仿真分析，首先需熟悉其两种颗粒接触模型：硬球模型和软球模型. 软球模型[22]存在几种主要的假设：① 模拟颗粒是一种形状为圆形的刚体，且颗粒间的接触均为点接触；② 颗粒间接触时可以允许有少量的重叠部分(见图5中δij， vi和vj表示颗粒运动方向， ri和rj为颗粒半径， rij为两个颗粒间的距离)；③ 当某一颗粒受到扰动后，只对相邻颗粒有一定的影响；④ 颗粒所受合力取决于颗粒间的相互作用. 而对于整个颗粒系统，既要满足本构方程，又需满足平衡方程，本构方程主要指颗粒接触模型中颗粒间相互作用力与位移的关系，平衡方程则是指经典力学中的牛顿第2运动定律.

图5 软球模型中颗粒接触碰撞[22]Fig.5 Particle contact collision in soft sphere model[22]

Wen等[22]通过利用DEM模拟了颗粒在不同形式下(滚筒和喷动床)的堆积过程，并分析了颗粒在这两种形势下的网格、色彩和位置等因素，评估了不同方法下颗粒搅拌指数的一些性能，研究表明，相邻距离法对颗粒的搅拌过程具有更好的适应性. Fan等[23]仿真了2维流化床上3种颗粒间无黏结力的弹射机制，并探讨了外部施加的作用力对颗粒的影响，认为颗粒之间的黏结力对颗粒的弹射和强度有影响. Cleary[24]在采用离散元模拟研磨机时，提出了一种对粉体或细颗粒多尺度模拟的方法，即微观尺度模型采用适宜的剪切单元，嵌入到传统的数字高程模型(digital elevation model, DEM)模型中；而宏观尺度模型则为相应的剪切单元给予剪切率和应力，然后通过微观尺度模型来预测粉体或细颗粒的研磨环境，并利用多尺度模型来仿真研磨的整个过程.

虽然这些模拟仿真颗粒堆积过程不是基于颗粒堆积模型，但有助于推动颗粒堆积模型的发展和应用. 如时金广[25]通过研究微小颗粒团聚的堆积状态，并通过利用EDEM软件用数值模拟颗粒在自然状态(图6)和振动两种方式下的堆积过程，并着重分析了振动时间和振动频率对颗粒堆积密实度的影响，对可压缩堆积模型进行了优化，能够使优化后的模型更加精确地预测混凝土混合料的堆积密实度.

图6 模拟自然状态下颗粒堆积[25]Fig.6 (Color online) Simulation of particle accumulation under the natural state[25]

3 颗粒堆积模型对比研究

近百年来，对颗粒堆积模型的研究一直处于发展阶段，研究者提出的模型均有自身的优点和局限性. 因此，不同的颗粒堆积模型对于混合料的堆积密实度的预测准确度不完全一致，即在某些局限特定的条件下虽然相差不大，但在普遍适应条件下还是存在很大差异.

Johansen等[26]通过将单一粒级的二元混合料进行混合实验，得到了堆积密实度实验值，对Aïm-Goff模型[12]和Toufar模型[11]进行了比较. 结果表明，当二元混合料的尺寸比小于0.22时，Aïm-Goff模型较准确；当二元混合料的尺寸比大于0.22时，Toufar模型则更准确.

Jones等[27-28]由实验所得的堆积密实度值，比较了文献[12,14,16-17]分别提出的4种颗粒堆积模型，并指出这些模型与其他模型的准确度不同；这些模型的预测准确度随着颗粒尺寸比的不同而变化，即当两个颗粒级别尺寸比大于0.4时，这4种模型对混合料的堆积密实度的预测准确度较好且相差不大.

Fennis[29]对当前使用较普遍的颗粒堆积模型进行了阐述和比较，如Furnas模型、Toufar模型、Dewar模型、LPDM模型和CPM模型，认为这些模型对于粗骨料在干堆积和湿堆积情况下的堆积密实度是一致的，但对于细颗粒体系，这些模型大都没考虑用湿堆积的方法来计算混合料堆积密实度. 由于CPM模型考虑了颗粒压实作用系数，被广大研究者认为是这些模型中预测堆积密实度最准确的一种，并直接被用于计算粗细骨料混合物的干湿堆积密实度.

Chan等[13,18]通过试验研究比较了不同颗粒堆积模型的准确性，根据模型中涉及到的颗粒间相互作用(松动效应系数a、 附壁效应系数b、 楔入效应系数c和压实指数k)， 把现有的颗粒堆积模型分为2参数模型(a, b)、 CPM模型(a,b, k)、 3参数模型(a,b, c)， 然后通过试验来比较这些模型的准确性. 结果表明，这些模型的准确性随着二元混合料颗粒的尺寸比值和体积分数的变化而变化，当颗粒尺寸比值大于0.65时，所有颗粒堆积模型的预测精度都较为准确；但当比值小于0.65时，2参数模型的计算准确度变得较低，甚至与实验值相差较大. 相对而言，3参数模型的计算精度是上述模型中最准确，也是应用最为广泛的模型.

各模型所预测堆积密实度的准确度对于材料的粒径、类别要求差异较大，且各模型的适用范围、特点也略有不同. 基于对上述各模型的深入研究，并结合模型的不断优化和演化，对其主要优点、局限性、适用范围做出相关总结，如表2.

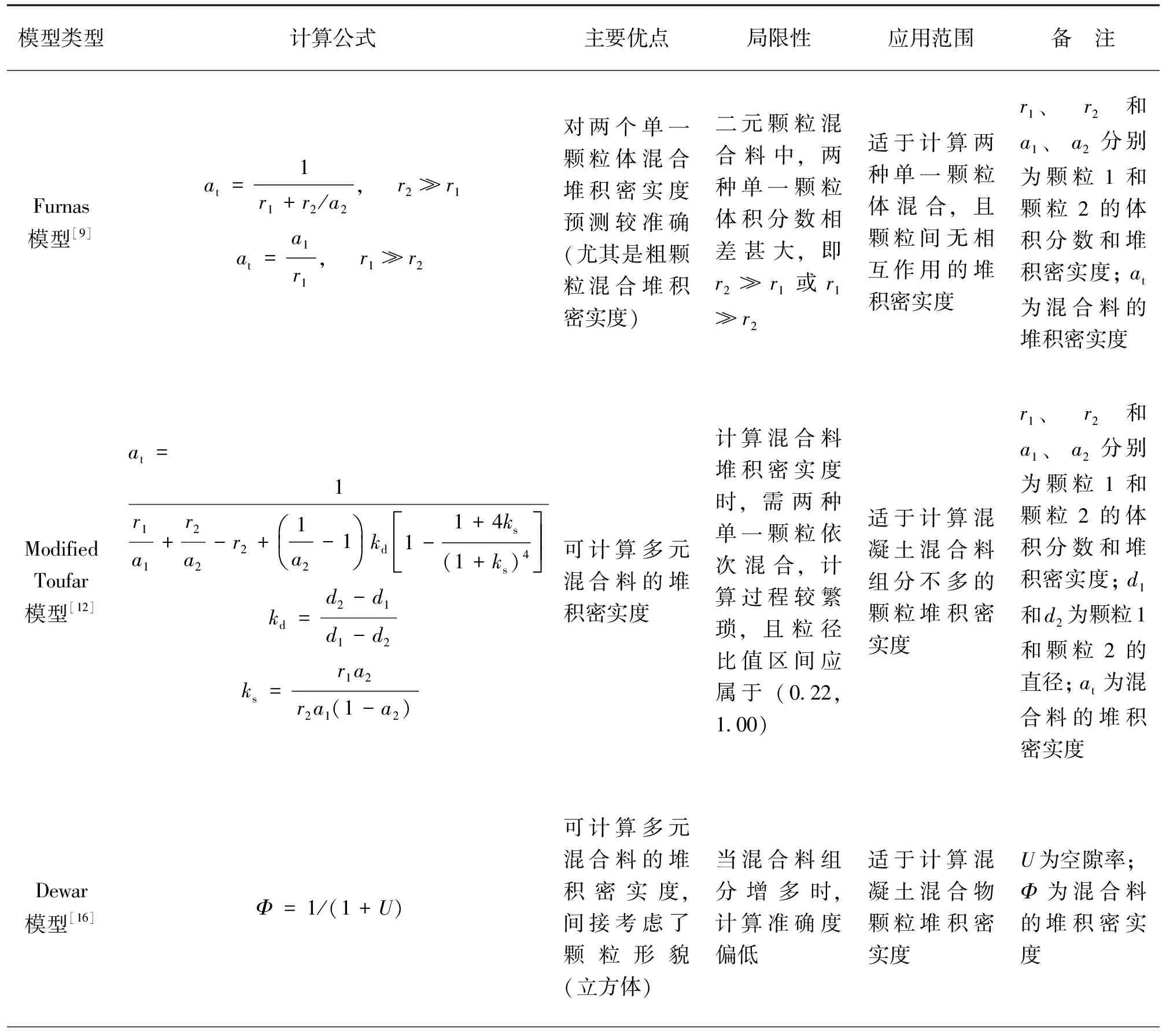
表2 颗粒堆积模型对比

(续表1)

4 基于颗粒堆积模型的应用研究

由于颗粒堆积密实度的研究具有重要的理论和实际意义，因而一直受到国内外研究者的关注. 研究人员利用颗粒堆积模型不但研究了混凝土混合料的堆积问题，且在此基础上研究了掺合料对整个混合料的堆积密实度的影响，进一步探讨了多尺寸颗粒堆积密实度对混凝土性能的影响[30-35].

牛全林等[36]根据Horsfield模型和Andrensen方程[7，37]探讨了矿渣超细粉对胶凝材料(水泥)的密实填充效应. 结果表明，根据Horsfield模型确定的超细填充粉，具有良好的填充效应，能有效改善硬化水泥浆体的孔径分布，而基于Andrensen 方程，将矿渣超细粉掺入水泥后颗粒的粒径分布状态与最紧密堆积仍存在较大的差距，这由Andrensen 方程可知

(3)

其中， D为颗粒粒径； Dmax为颗粒体中最大颗粒粒径； n为模型分布指数，取值为1/3.

陈延信等[38]基于Andrensen方程和CPM模型及实验研究探讨了提高粉体堆积密实的理论. 结果表明，用CPM模型来预测粉体颗粒的堆积密实度实验值为0.698 5，模型计算值为0.695 1，相对误差仅为0.810 0%. 用该模型预测粉体颗粒体系的堆积密实度具有较高的可靠性，且经过模型调质后可以使混合体系的堆积效率提高6.0%.

龙广成等[39]基于 Aïm-Goff 模型定量分析了超细粉煤灰、磨细矿渣及硅粉3种矿物掺合料对新拌水泥净浆堆积密实度的作用变化，研究了掺入这3种矿物料后浆体的流动性与相对密实度之间的关联性，探讨了矿物掺合料的密实填充作用对水泥胶砂抗压强度的影响. 结果表明，在所做试验掺量范围内，这3种矿物掺合料能较大地改善新拌水泥浆体的密实度，其中硅灰对颗粒体系的作用效果最佳. 同时，新拌浆体相对密实度提高后，硬化后浆体的抗压强度也有所提高.

Binici等[40-41]研究了掺入不同细度的掺合料(高炉矿渣和天然火山灰)对混合料堆积密实度的影响. 结果表明，高炉矿渣和天然火山灰细度越小，混合料的堆积密实度越大，对混凝土强度的提高越明显.

Kwan等[42-43]基于三参数颗粒堆积模型研究了粉煤灰掺量为0～60%时对水泥基复合材料密实度、流动度和强度的影响. 结果表明，掺量为 40%的超细粉煤灰对水泥基材料的堆积密实度的贡献最大，且超细粉煤灰有助于提高浆体黏度.

Ghoddousi等[44]研究了颗粒堆积密实度对自密实混凝土稳定性和流变性能的影响. 研究表明，对于粗细砂混合，总是存在一个最佳值，使空隙率最低，松动效应和附壁效应减少. 研究同时得到了颗粒堆积密实度的一个优化值，为0.804，比具有低静态离析的最大堆积密实度值0.807略小. 研究者认为利用湿堆积来计算自密实混凝土是一种可行的方法.

Nassim 等[45]通过比较利用可压缩堆积模型、国内规范(JGJT283—2012自密实混凝土应用技术规程)和欧洲标准(BS EN 206-1)设计了自密实混凝土配合比. 结果表明，利用这3类标准进行自密实混凝土配合比设计，可以得到28 d平均抗压强度为(72.0±2.5)MPa的中等强度混凝土；同时，利用可压缩堆积模型进行设计的混凝土配合比中所使用胶凝材料用量相对较低，约为400 kg/m3. 因此，利用可压缩堆积模型来制备自密实混凝土不但可以满足工作性能和力学性能的需求，而且经济环保.

龚建清[46]论述了基于CPM模型计算粉体混合料堆积密实度时所存在的问题和相对应的解决方法，并利用CPM模型分析了微粉在不同颗粒粒径和掺入量的情况下，对颗粒混合料体系堆积密实度的影响. 实验表明，当矿物微粉在一定掺量范围内，颗粒体系的堆积密实度随着掺量的增加而提高，其相对应的抗压强度也不断提高；但当掺量超过某一值时，颗粒体系的堆积密实度不再随掺量的增加而提高. 同时，研究者从矿物细掺料的密实填充效应角度，探讨了矿物微粉的级配效应对超高性能混凝土性能的影响，认为当超细粉煤灰和硅灰双掺后颗粒体系比单掺超细粉煤灰后颗粒体系的颗粒堆积结构更加密实，其颗粒级配更好，在水胶比较低(0.22)的情况下，密实填充效应对颗粒体系堆积结构更加密实的浆体作用更加明显，更能充分发挥这些矿物微粉颗粒对颗粒体系结构的密实填充效应，对浆体抗压强度的提高作用也就越明显.

曹荣奎[47]利用CPM模型分析了矿物微粉(粉煤灰、矿渣和硅灰)以不同比例混合后，对其火山灰效应和颗粒堆积密实度的影响；并重点对火山灰效应和复合火山灰效应进行了模拟研究，通过数学工具拟合相关的参数(如堆积密实度作用值与火山灰效应强度贡献率间的关联性)，提出了超高性能混凝土混合料配合比设计方法.

聂晶[48]根据CPM模型，对水泥基复合材料堆积密实度进行了研究，如水泥-矿渣体系、水泥-粉煤灰体系等，并利用Andreasen方程计算了上述复合材料体系最紧密堆积状态下的颗粒粒径分布. 研究结果表明，Andreasen计算得到的颗粒粒径分布下体系的堆积密实度与CPM模型计算结果一致；同时，研究者认为矿物微粉对水泥颗粒堆积体系的密实效应很大程度由矿物微粉颗粒的平均粒径与水泥颗粒的平均粒径之比决定.

李丙明[49]利用CPM模型对钢渣、矿渣、超细粉煤灰(平均粒径为5.51 μm)3种微粉掺入到水泥体系后混合料实际堆积密实度的变化进行了研究. 结果表明，只有当钢渣、矿渣与超细粉煤灰复合掺入水泥后，粉体的堆积密实度才能提高；且粉煤灰的掺加比例越大，混合料的密实度越高. 研究者同时研究了上述3种复合微粉以不同掺量替代水泥后颗粒级配与堆积密实度之间的关系，及对混凝土性能的影响.

丑凯[50]在将CPM模型应用于粉体颗粒体系(包括单掺硅灰体系和双掺硅灰和粉煤灰体系)的堆积密实度计算时，发现堆积密实度与火山灰效应在不同水胶比条件下存在一定关联，提出了这两种不同体系在28 d标准养护条件下，混凝土的堆积密实度贡献率与火山灰效应强度贡献率之间的拟合通式为

1)单掺硅灰体系

(4)

其中， y为火山灰效应贡献率； x为堆积密实度贡献率； A1、 A2、 x0和dx为拟合曲线参数.

2)双掺体系

(5)

其中， y为火山灰效应贡献率； x为堆积密实度贡献率； y0、 xc、 A和w为拟合曲线参数.

最后，丑凯[50]利用数学工具将堆积密实度与火山灰效应进行合理量化，并通过实例来验证两者之间的关联性，提出了一种有效设计超高性能混凝土配合比的方法.

何振伟[51]通过利用水化动力学理论模型，并基于CPM模型-粉煤灰混凝土强度预测模型和基于CPM 的弹性模量三重球模型的基础上，提出了持续应力下密封早龄期混凝土抗压强度和弹性模量根据时间不断变化而发展的理论模型，并根据实验对模型参数进行拟合，对新模型相关参数进行分析. 结果表明，所提新模型能很好地预测早期钢管混凝土力学性能的发展变化. 这里提及的三重球模型是指将混凝土混合料看成由核心为浆体球体、中间为骨料、外层是浆体组成的一个完整球体，如图7.

图7 三重球模型基本单元[51]Fig.7 The basic unit of concrete based on the triple-sphere model[51]

Fennis[29]在CPM模型的基础上，提出了与混凝土性能相关的两个指数，即胶凝材料颗粒间隙指数和用水量富余指数，并将实际状态下胶凝材料颗粒间隙指数(cement space factor， CSF)定义为

(6)

其中, Kb为胶凝材料颗粒的叠加压实值； Vb为稳定颗粒结构状态下固体颗粒的体积； Vw为混合料拌和时总的需水量.

(7)

其中， Vcem为单位体积混凝土中水泥含量； Va为单位体积混凝土中粗细骨料含量； Vm为单位体积混凝土中矿物掺合料含量； Bm为修正系数； at为混合料颗粒实际堆积密实度.

陈瑾祥[52]的实验研究表明，水灰比为0.45～0.57的纯水泥混凝土，基于用水量富余指数所提出的工作性能预测模型与实测工作性能两者之间的相关系数可达到0.96；而基于CSF指数所提出的标准混凝土强度预测模型与实测强度值之间的相关系数也较高，即3、7和28 d的相关系数分别为0.87、0.93和0.98.

5 结 语

综上研究认为，颗粒堆积模型是基于数学方程描述不同尺寸颗粒间几何作用的计算方法，利用颗粒堆积模型可以计算混合料的堆积密实度并对其进行优化，使混合料达到物理最紧密的堆积状态，从而减小颗粒体系的空隙率，减少水泥用量，最终实现绿色混凝土的配合比优化设计. 目前对各类型颗粒堆积模型的基础及应用研究尚可从以下入手完善.

1)对于固体颗粒体系，虽然大多数颗粒模型对其堆积密实度预测都较准确，但在应用这些模型预测颗粒堆积密实度时，均假设所有堆积颗粒的形状是同一的，没有考虑颗粒的形貌特征影响，故与堆积颗粒的真实情况不一致，使得预测理论值与实测值存在一定误差. 建议引入形貌参数或形貌函数，以提高颗粒堆积模型的预测精度.

2)对于细颗粒体系，因其颗粒之间除了重力作用之外，还需考虑范德华力和静电力等作用，从而使得颗粒之间的相互作用变得复杂. 因此有必要对颗粒堆积模型的作用机理进行学入研究.

3)利用颗粒堆积模型，计算粗细骨料-胶凝材料混合堆积密实度的研究目前存在空白.

4)颗粒堆积模型在混凝土中的应用，主要侧重于计算混凝土混合料颗粒的物理堆积密实度，而胶凝材料水化后颗粒系统结构会发生变化，这对颗粒堆积密实度会产生影响，而已有的颗粒堆积模型不再适用于准确计算其堆积密实度. 如何考虑物理堆积和胶凝材料化学反应所产生的对堆积密实度的协同作用效应，还需更为系统深入地研究.

5)随着高性能计算机的发展，计算仿真模拟在混凝土中的应用已成为研究者的有效工具，但目前对于混凝土硬化全过程较全面的模拟仿真分析仍有待推动.

/ References：

[1] Gao Tianming, Shen Lei, Shen Ming, et al. Analysis on differences of carbon dioxide emission from cement production and their major determinants[J]. Journal of Cleaner Production, 2015, 103(23): 160-170.

[2] Suhendro B. Toward green concrete for better sustainable environment[J]. Procedia Engineering, 2014, 95(95): 305-320.

[3] Yoshioka K, Obata D, Nanjo H, et al. New ecological concrete that reduces CO2emissions below zero level new method for CO2capture and storage[J]. Energy Procedia, 2013, 37: 6018-6025.

[4] HiguchiI T, Morioka M, Yoshioka I, et al. Development of a new ecological concrete with CO2emissions below zero[J]. Construction and Building Materials, 2014, 67: 338-343.

[5] Yu R, Spesz P, Brouwers H J H. Development of an eco-friendly ultra-high performance concrete (UHPC) with efficient cement and mineral admixtures uses[J]. Cement and Concrete Composites, 2015, 55(1): 383-394.

[6] Westman A E R, Hugill H R. The packing of particles[J]. Journal of the American Ceramic Society ，1930, 13(10): 767-779.

[7] Andreason A H M. Uber die beziehung zwischen kornabstufung und zwischenraum in produckten aus losen kornern[J]. Kolloid Z, 1930, 50(3): 217-228.

[8] Dinger D R, Funk J E. Particle packing: review of packing theories[C]// Proceeding of Fine Particle Society 13th Annual Meeting. Chicago, USA: American Ceramic Society, 1982.

[9] Furnas C C. Grading aggregates I-mathematical relations for beds of broken solids of maximum density[J]. Industrial and Engineering Chemistry， 1931, 23(9): 1052-1028.

[10] Toufar W, Born E K M. Berechnung der packungsdichte von korngemischen[J]. Aufbereitungs-Technik, 1977, 18(11): 603-608.

[11] Aïm R B, Goff P L. Effet de paroi dans les empilements désordonnés desphères et application à la porosité de mélanges binaries[J]. Powder Technology, 1968,1(5): 281-290.

[12] Goltermann P, Johansen V, Palbol L. Packing of aggregates: an alternative tool to determine the optimal aggregate mix[J]. American Concrete Institute Materials Journal, 1997, 94(5)：435-443.

[13] Chan K W, Kwan A K H. Evaluation of particle packing models by comparing with published test results[J]. Particuology, 2014, 16(5): 108-115.

[14] Stovall T, Bull M. Linear packing density model of grain mixtures[J]. Powder Technology, 1986, 48(1): 1-12.

[15] 王海兵,刘 咏,黄伯云, 等. 粉末颗粒线性堆积密实度模型的改进[J].粉末冶金技术, 2001, 19(4):208-211. Wang Haibing, Liu Yong, Huang Boyun, et al. Improvement of linear packing density model of powder particles[J]. Powder Metallurgy Technology, 2001, 19(4):208-211.(in Chinese)

[16] Dewar J D. Computer modelling of concrete mixtures[M]. London: Routledge, 1998.

[17] Larrard F. Concrete mixture proportioning: a scientific approach[M]. London: Routledge, 1999.

[18] Kwan A K H. A 3-parameter particle packing model incorporating the wedging effect [J]. Powder Technology, 2013, 237(3): 172-179.

[19] Wong V, Kwan A K H. A 3-parameter model for packing density prediction of ternary mixes of spherical particles[J]. Powder Technology, 2014, 238(1): 357-367.

[20] Kwan A K H, Wong V, Fung W W S. A 3-parameter packing density model for angular rock aggregate particles[J]. Powder Technology, 2015, 239(2): 154-162.

[21] Knop Y, Peled A. Packing density modeling of blended cement with limestone having different particle size[J]. Construction and Building Materials, 2016, 102: 44-50.

[22] Wen Yuanyun, Liu Malin, Liu Bing, et al. Comparative study on the characterization method of particle mixing index using DEM method[J]. Procedia Engineering, 2015, 102: 1630-1642.

[23] Fan Haojie, Mei Dengfei, Tian Fengguo, et al. DEM simulation of different particle ejection mechanisms in a fluidized bed with and without cohesive interparticle forces[J]. Powder Technology, 2016, 288: 228-240.

[24] Cleary P W. A multiscale method for including fine particle effects in DEM models of grinding mills[J]. Minerals Engineering, 2015, 84: 88-99.

[25] 时金广.基于堆积模型的胶凝材料颗粒系统的离散单元法分析仿真研究[D]. 深圳：深圳大学，2016. Shi Jinguang. The research of discrete element method simulation for particle packing-based cementitious materials[D]. Shenzhen: Shenzhen University, 2016.(in Chinese)

[26] Johansen V, Andersen P J. Particle packing and concrete properties[J]. Materials Science of Concrete ， 1989, 2: 111-146.

[27] Jones M R, Zheng L, Newlands M D. Comparison of particle packing models for proportioning concrete constituents for minimum voids ratio[J]. Materials and Structures, 2002, 35(5): 301-309.

[28] Standish N, Borger D E. The porosity of particulate mixtures[J]. Powder Technology, 1979, 22(1): 121-125.

[29] Fennis S A A M. Design of ecological concrete by particle packing optimization[D]. Netherlands: Delft University of Technology, 2011.

[30] Kwan A K H, Wong H H C. Packing density of cementitious materials: packing and flow of OPC+PFA+CSF[J]. Materials and Structures, 2008, 41: 773-784.

[31] Gallias J L, Kara-Ali R, Bigas J P. The effect of fine mineral admixtures on water requirement of cement pastes[J]. Cement Concrete Composites, 2000, 30(10): 1543-1549.

[32] Peng Yanzhou, Hu Shuguang, Ding Qingjun. Dense packing properties of mineral admixtures in cementitious material[J]. Particuology, 2009, 7(5): 399-402.

[33] Knop Y, Peled A. Setting behavior of blended cement with limestone: influence of particle size and content[J].Materials and Structures, 2016, 49(1): 439-452.

[34] Felekogˇlu B. Effects of PSD and surface morphology of micro-aggregates on admixture requirement and mechanical performance of micro-concrete[J]. Cement Concrete Composites, 2007, 29(6): 481-489.

[35] Knop Y, Peled A, Cohen R. Influence of limestone particle size distributions and contents on blended cement properties[J]. Construction and Building Materials, 2014, 71: 26-34.

[36] 牛全林，冯乃谦，杨 静.矿渣超细粉作用机理的探讨[J].建筑材料学报, 2002, 5(1)：84-89. Niu Quanlin, Feng Naiqian, Yang Jing. Discussion on the action mechanism of superfine slag powder[J]. Journal of Building Materials, 2002, 5(1)：84-89.(in Chinese)

[37] Fayed M E, Otten L. Handbook of powder science and technology [M]. New York: Chapman and William Hall, 1997.

[38] 陈延信,吴 锋,胡亚茹. 提高粉体堆积密实度的理论与实验研究[J]. 煤炭转化, 2012(1): 40-43. Chen Yanxin, Wu Feng, Hu Yaru. Theoretical and experimental study on increasing the bulk density of powder[J]. Coal Conversion, 2012(1): 40-43.(in Chinese)

[39] 龙广成，谢友均，王新友.矿物掺合料对新拌水泥浆体密实性能的影响[J].建筑材料学报, 2002, 5(1): 21-25. Long Guangcheng, Xie Youjun, Wang Xinyou. Effect of mineral admixtures on the compaction property of fresh cement paste[J]. Journal of Building Materials, 2002, 5(1)：21-25.(in Chinese)

[40] Binici H, Aksogan O, Cagatay I H, et al. The effect of particle size distribution on the properties of blended cements incorporating GGBFS and natural pozzolan (NP) [J]. Powder Technology, 2007, 177(3): 140-147.

[41] Givi A N, Rashid S A, Aziz F N A, et al. Assessment of the effects of rice husk ash particle size on strength, water permeability and workability of binary blended concrete[J]. Construction and Building Materials, 2008, 24(11): 2145-2150.

[42] Kwan A K H, Chen J J. Adding fly ash microsphere to improve packing density, flowability and strength of cement paste[J]. Powder Technology, 2013, 234:19-25.

[43] Kwan A K H, Li Y. Effects of fly ash microsphere on rheology, adhesiveness and strength of mortar[J]. Construction and Building Materials, 2013, 42: 137-45.

[44] Ghoddousi P, Javid A A S, Sobhani J. Effects of particle packing density on the stability and rheology of self-consolidating concrete containing mineral admixtures[J]. Construction and Materials, 2014, 53: 102-109.

[45] Nassim S, Mahfoud B. Composition of self compacting concrete (SCC) using the compressible packing model, the chinese method and the european standard[J]. Construction and Building Materials, 2013, 43: 382-328.

[46] 龚建清. 超高性能混凝土的级配效应研究[D]. 长沙：湖南大学, 2008. Gong Jianqing. Study on the gradation effect of ultra high performance concrete[D]. Changsha: Hunan University, 2008.(in Chinese)

[47] 曹荣奎. 基于CPM模型和比强度法的超高性能混凝土配合比设计研究[D]. 长沙：湖南大学, 2008. Cao Rongkui. Study on mix proportion design of ultra-high performance concrete based on CPM model and specific strength[D]. Changsha: Hunan University, 2008.(in Chinese)

[48] 聂 晶. 基于可压缩堆积模型的水泥基复合材料性能研究[D]. 长沙：湖南大学, 2008. Nie Jing. Study on performance of cement-based composite materials based on compressible packing model[D]. Changsha: Hunan University, 2008.(in Chinese)

[49] 李丙明. 低碱度钢渣配制复合胶凝材料研究[D]. 西安： 西安建筑科技大学, 2009. Li Bingming. The study on preparing composite cementitious materials with low-alkalinity steel slag[D]. Xi’an: Xi'an University of Architecture and Technology, 2009.(in Chinese)

[50] 丑 凯. 超高性能混凝土堆积密实度和火山灰效应量化研究[D]. 长沙：湖南大学, 2010. Chou Kai. Quantitative analysis on packing density and pozzolanic effect of ultra-high performance concrete[D]. Changsha: Hunan University, 2010.(in Chinese)

[51] 何振伟. 持续应力下密封早龄期混凝土力学性能依时发展规律研究[D]. 北京：北京交通大学, 2013. He Zhenwei. Development of mechanical properties of sealed concrete in early age under sustained stress action[D]. Beijing: Beijing Jiaotong University, 2013.(in Chinese)

[52] 陈瑾祥. 基于可压缩堆积模型的绿色混凝土材料性能研究[D]. 深圳: 深圳大学, 2015. Chen Jinxiang. Compressible packing model based of green concrete[D]. Shenzhen: Shenzhen University, 2015.(in Chinese)

【中文责编：坪 梓；英文责编：之 聿】

Application of particle packing model in concrete

Long Wujian†, Zhou Bo, Liang Peijian, and Sun Roujia

Guangdong Provincial Key Laboratory of Durability for Marine Civil Engineering, College of Civil Engineering,Shenzhen University, Shenzhen 518060, Guangdong Province, P.R.China

The main advantages and limitations of particle packing models, as well as their applications in the field of composite particle systems are pointed out by comparing and analyzing the differences among various particle packing models. The analysis show that, in order to reduce the void volume and achieve the most compact accumulation state of the composite particle system, the particle packing model can be used to calculate the packing density, thus the volume of cementitious materials in the concrete can be reduced and the optimal design of low binder green concrete can be realized.

concrete; particle packing model; packing density; particle system; loosening effect; wall effect; void ratio; mix proportions

Received：2016-08-29；Accepted：2016-11-20

Foundation：National Natural Science Foundation of China (51278306，51578341); Shenzhen Science and Technology Project (JCYJ20140418095735540)

† Corresponding author：Associate professor Long Wujian. E-mail: longwj@szu.edu.cn

：Long Wujian, Zhou Bo, Liang Peijian, et al. Application of particle packing model in concrete[J]. Journal of Shenzhen University Science and Engineering, 2017, 34(1): 63-74.(in Chinese)

TU 528

A

10.3724/SP.J.1249.2017.01063

国家自然科学基金资助项目(51278306，51578341)；深圳市科技计划资助项目(JCYJ20140418095735540)

龙武剑(1977—)，男，深圳大学副教授、博士. 研究方向：高性能混凝土材料设计及性能. E-mail： Longwj@szu.edu.cn

引 文：龙武剑，周 波，梁沛坚，等. 颗粒堆积模型在混凝土中的应用[J]. 深圳大学学报理工版，2017，34(1)：63-74.