纵向磁场中载流单层碳纳米管的振动与失稳
2017-01-19周攀峰郑华升
李 明,周攀峰,郑华升
(武汉科技大学冶金工业过程系统科学湖北省重点实验室,湖北 武汉,430065)
纵向磁场中载流单层碳纳米管的振动与失稳
李 明,周攀峰,郑华升
(武汉科技大学冶金工业过程系统科学湖北省重点实验室,湖北 武汉,430065)
以非局部弹性理论为基础,采用Euler-Bernoulli梁模型,并考虑纳米管管形区域内滑移边界条件以及小尺度效应,研究了纵向磁场中单层载流碳纳米管的振动与失稳问题。根据哈密顿原理获得碳纳米管的横向振动方程和边界条件。应用微分变换法(DTM)对此高阶偏微分方程进行求解,通过数值计算分析磁场强度、小尺度参数和Knudsen数对单层载流碳纳米管振动频率和稳定性的影响。结果表明,小尺度参数和Knudsen数越大,系统基频及临界流速就越低,系统的稳定区域也越小;纵向磁场强度增加到一定程度后,磁场作用将明显提高系统的基频及临界流速,也即增大了系统的稳定区域。
碳纳米管;纵向磁场;载流;微分变换法;振动;失稳;临界流速
碳纳米管是一种重要的纳米材料,具有小尺度、低密度、高强度和高硬度等特性,加之完美的空心圆柱形几何结构,其已成为纳米尺度下流体储藏与输运的重要载体[1-2]。与之相应,作为一种典型的小尺度高流速流固耦合系统,载流碳纳米管的动力学特性也吸引了国内外研究人员的大量关注。Wang等[3]应用非局部Euler-Bernoulli梁模型研究载流双层碳纳米管的固有频率和屈曲失稳特性,发现了小尺度参数对碳纳米管振动频率的影响规律。梁峰等[4]应用非局部黏弹性夹层梁模型分析双参数弹性介质中输送脉动流碳纳米管的稳定性,证明了非局部效应对载流碳纳米管的影响特性。基于载流碳纳米管的流场特征尺度变小以及Knudsen数(定义为流体分子平均自由程与流场的特征尺度之比)大于0.01的特性,Mirramezani等[5]考虑管形区域内滑移边界条件,研究了Knudsen数对纳米级载流管振动稳定性的影响。
近年来,碳纳米管在生物医药领域(如抗肿瘤药物的靶向输送)以及纳机电系统(NEMS)中得到越来越广泛的应用,而由于磁场具有优异的智能控制特性,其在碳纳米管载流中的应用也开始受到关注,但针对碳纳米管在磁场中的磁-力耦合特性的研究成果在现阶段还相对较少。Murmu等[6]基于非局部弹性理论分析了纵向磁场中双层碳纳米管的横向振动问题。Kiani[7]应用非局部Rayleigh梁模型以及Maxwell’s方程研究了三维磁场作用下单层碳纳米管的纵向、横向振动特性。本文以非局部弹性理论为基础,采用Euler-Bernoulli梁模型,考虑碳纳米管的小尺度效应和稀薄效应,着重研究单层简支载流碳纳米管在纵向磁场作用下的振动与失稳问题。
1 振动控制方程与边界条件
图1所示为单层简支碳纳米管,其长度为L,外径为D,横截面积为A,弯曲刚度为EI,E为材料弹性模量。每单位长度上纳米管的质量和内部流体的质量分别为mc和mf。假定振动时管道只发生横向面内振动,且不考虑重力以及管道外部拉、压力的影响。W(X,T)为纳米管振动的横向位移,其中,X为纳米管的纵向坐标,T为时间。

图1 纵向磁场中单层简支载流碳纳米管
对于载流碳纳米管,Knudsen数大于0.01,参照文献[5]采用滑移边界条件,将管内流体的平均流速修正为Uavg,slip= VCF·Uavg,(no-slip),其中,Uavg,slip与Uavg,(no-slip)分别为滑移与无滑移边界条件下流体的平均流速,VCF为平均流速修正因子,定义如下[5]:
(1)
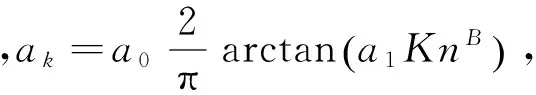
根据微观Maxwell’s方程[6],在纵向磁场中,由磁场引起的作用于单层碳纳米管横向单位长度上的洛伦兹力可表示为:
(2)
式中:η为磁导率;HX为纵向上的磁场强度。
考虑小尺度效应,以非局部弹性理论为基础,应用哈密顿原理可以得到载流纳米管在纵向磁场中的运动方程为:
(3)
式中:e0a是纳米材料中引起结构小尺度效应的参数。
文献[8]已证明,对于两端简支的载流纳米管,仍可以采用局部连续理论下的边界条件,即:
(4)
2 振动控制方程的求解

(5)
以及无量纲简支边界条件
(6)

(7)
根据DTM运算法则[8],可得到式(7)的微分变换形式
[1-μ(u2-ψ)]·(k+4)!·Φ(k+4)-
(u2-ψ-μΩ2)·(k+2)!·Φ(k+2)+
Ω2·k!·Φ(k)=0
(8)
和相应的简支边界条件微分变换形式
Φ(0)=Φ(2)=0
(9)

(10)
令Φ(1) = C1, Φ(3) = C2,再通过式(8)、式(9)进行迭代,求得Φ(k),k = 4,5,…,N。然后将Φ(k)代入式(10),可得到以下两个方程:
(11)
式中:aij是关于Ω和其他系统参数的多项式。式(11)有平凡解的条件是其系数矩阵行列式为零,由此即可获得系统的复数特征值Ω,其虚部Im(Ω)是系统的无量纲固有频率,其实部Re(Ω)与阻尼有关。已有研究表明[10],当Im(Ω) = 0 时,简支纳米管系统将因发散而出现屈曲失稳,故使Im(Ω)由正变为零的流速称为系统的屈曲临界流速ucr。
3 数值算例
对于简支载流纳米管在纵向磁场中的动力特性分析,本文采用的参数为[6,11]:碳纳米管密度ρc= 2300 kg/m3,外层半径R0=3 nm,长径比L/2R0=40,壁厚td= 0.1 nm,弹性模量E=3.4 TPa,磁导率η= 4π×10-7H/m,质量比系数β=0.1。DTM的计算精度取决于截断项数N的取值,N值越大计算结果越接近精确解,本文取N=40,经过验证,此条件下已能保证一阶模态的解具有足够精确。
3.1 频率分析
鉴于内部流体的流动行为将对载流纳米管的振动特性产生影响,故表1首先给出了载流纳米管中流体无量纲流速u、小尺度参数μ、Knudsen数Kn均为零时,纳米管一阶无量纲固有频率与纵向磁场强度之间的变化规律。由表1可见,当纵向磁场强度HX不低于107A/m时,随着磁场的增强,简支纳米管无量纲基频才有了显著的提高,也就是说,纵向磁场必须达到一定强度后才能对纳米管的振动效果产生影响。

表1 无量纲基频随纵向磁场强度的变化(u=0,μ=0,Kn=0)
图2给出了简支载流纳米管在无纵向磁场和纵向磁场强度为5×107A/m两种情况下,系统一阶无量纲特征值的虚部与实部随管内流体无量纲流速的变化情况,此时仍取μ=0、Kn=0。由图2可以看出,对于不同的无量纲流速,纵向磁场的作用提高了该流速下系统的无量纲基频数值,且使系统的分叉现象在较高流速下产生,这意味着外加纵向磁场可以降低内部流体对载流纳米管固有频率的影响,并且提升系统的稳定性。

(a) 虚部

(b) 实部
图3和图4给出了简支载流纳米管在无纵向磁场与纵向磁场强度为5×107A/m两种情况下,分别取不同小尺度参数(此时Kn=0)和不同Knudsen数(此时μ=0)时,系统一阶无量纲固有频率与管内流体无量纲流速的变化关系。由图3和图4可以看出,无论有没有纵向磁场作用,随着小尺度参数以及Knudsen数的增加,相同流速下系统的固有频率均会降低,因此系统的稳定性也会出现不同程度的减弱。
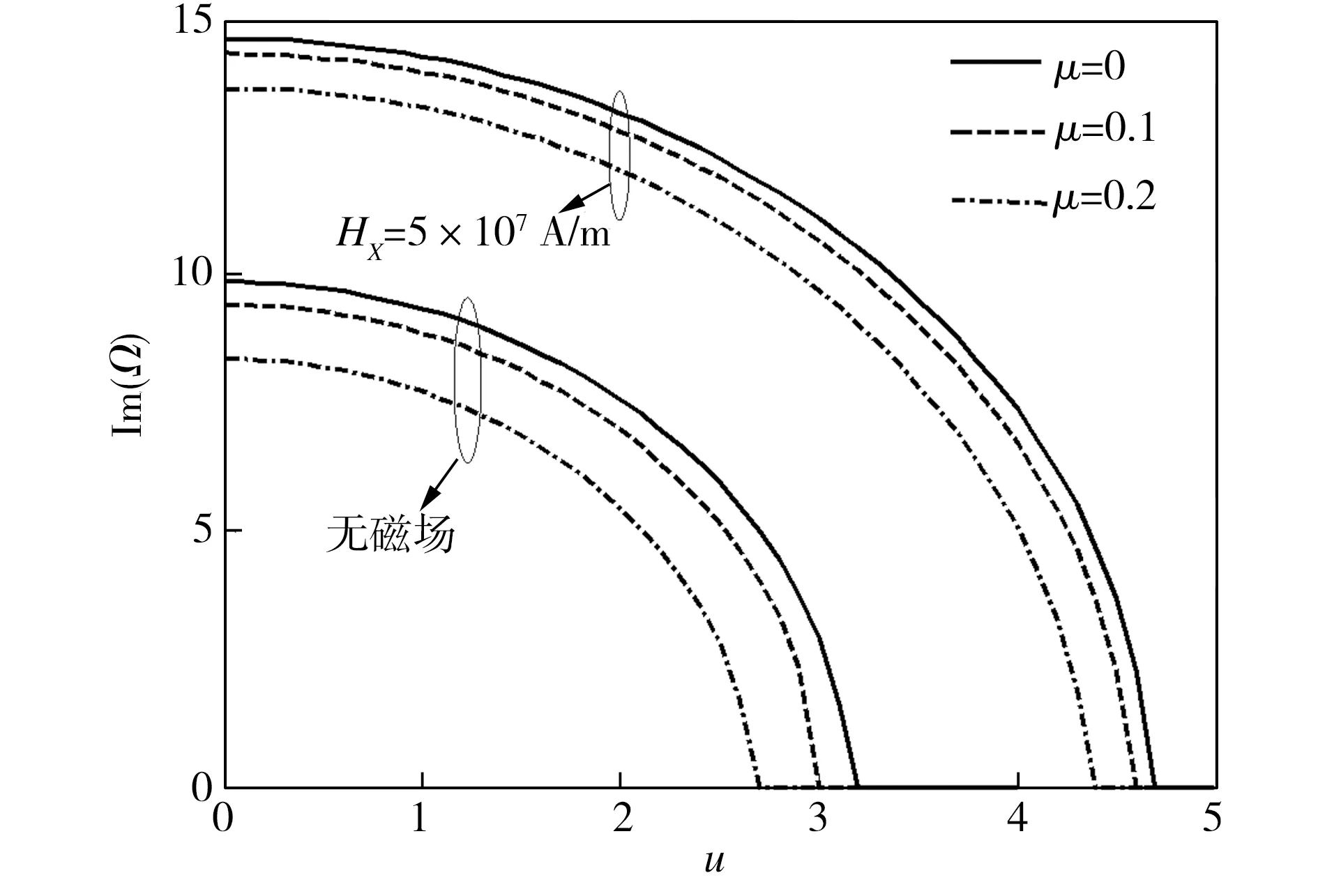
图3 不同小尺度参数下无量纲基频随无量纲流速的变化(Kn=0)
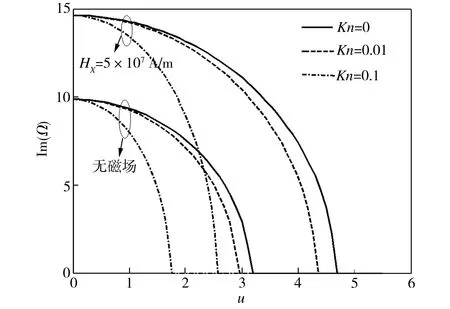
图4 不同Knudsen数下无量纲基频随无量纲流速的变化(μ=0)
3.2 稳定性分析
在流固耦合问题的研究中,特别是对于载流纳米管这类柔性结构,系统稳定性的分析以及系统临界流速的计算都是关键内容。图5(a)给出了纵向磁场强度不同时,系统无量纲临界流速随Knudsen数的变化情况,此时取μ=0.1。图5(b)给出了小尺度参数取值不同、纵向磁场强度HX=5×107A/m时,系统无量纲临界流速ucr随Knudsen数的变化情况。
由图5可以看出,Kn值在0.0001~0.01范围内时,影响临界流速的因素主要是外加纵向磁场强度和小尺度参数而不是Kn值,具体表现为:磁场强度越大,临界流速越高,载流纳米管的稳定区域越大;小尺度参数越大,临界流速越低,载流纳米管的稳定区域越小。Kn值在0.01~0.1范围内时,流体处于滑移流动区,稀薄效应开始体现,此时磁场强度、小尺度参数仍对临界流速产生相应的影响且规律与Kn值位于0.0001~0.01区间的规律相同,但影响程度降低,而这时Knudsen数对临界流速的影响开始显现,即随着Kn值的增加,临界流速逐渐降低,相应的载流纳米管稳定区域逐渐减小。超过上述范围之后,Knudsen数逐渐成为影响临界流速的主要因素,而其他参数的影响程度则逐渐减弱。

(a)不同磁场强度(μ=0.1)
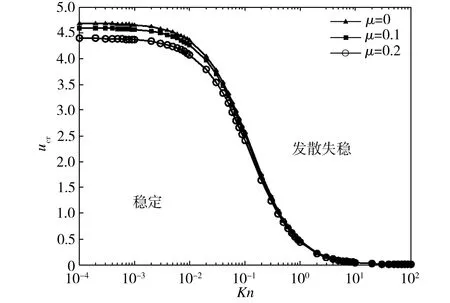
(b) 不同小尺度参数(HX=5×107 A/m)
4 结语
本文基于非局部Euler-Bernoulli梁模型,考虑载流纳米管管形区域内的滑移边界条件,应用哈密顿原理建立单层简支载流碳纳米管的振动控制方程,采用DTM法对这个高阶偏微分方程进行求解,分析了纵向磁场作用下该系统的振动与失稳问题,分别讨论了纵向磁场强度、小尺度参数以及Knudsen数对系统基频和临界流速的影响。从数值算例分析来看,载流纳米管小尺度效应以及稀薄效应越明显,系统基频及临界流速就越低,系统的稳定区域也越小;而磁场强度增加到一定数值后,磁场作用将明显提高系统的基频及临界流速,也即增大了系统的稳定区域。由于失稳临界流速对于载流纳米管的纳米力学特性有明显的影响,因此本文所得结论可为工程纳米流体机械的设计分析提供一定的理论参考。
[1] Soltani P, Farshidianfar A. Periodic solution for nonlinear vibration of a fluid-conveying carbon nanotube, based on the nonlocal continuum theory by energy balance method[J]. Applied Mathematical Modelling, 2012, 36(8):3712-3724.
[2] Xia W, Wang L. Vibration characteristics of fluid-conveying carbon nanotubes with curved longitudinal shape[J]. Computational Materials Science, 2010, 49(1): 99-103.
[3] Wang L, Ni Q, Li M. Buckling instability of double-wall carbon nanotubes conveying fluid[J]. Computational Materials Science, 2008, 44(2):821-825.
[4] 梁峰,包日东.基于非局部效应和表面效应的输流碳纳米管稳定性分析[J].力学与实践,2012,36(1): 48-53.
[5] Mirramezani M, Mirdamadi H R. The effects of Knudsen-dependent flow velocity on vibrations of a nano-pipe conveying fluid[J]. Archive of Applied Mechanics, 2012,82(7):879-890.
[6] Murmu T, McCarthy M A, Adhikari S. Vibration response of double-walled carbon nanotubes subjected to an externally applied longitudinal magnetic field: a nonlocal elasticity approach[J]. Journal of Sound and Vibration, 2012, 331(23): 5069-5086.
[7] Kiani K. Vibration and instability of a single-walled carbon nanotube in a three-dimensional magnetic field[J]. Journal of Physics and Chemistry of Solids, 2014, 75(1): 15-22.
[8] Li M, Zheng H, Luo X, et al. Energy meaning of small-scale effect on free vibration of carbon nanotubes[J]. International Journal of Nanomanufacturing, 2014, 10(5/6): 415-423.
[9] Chen C K, Ho S H. Transverse vibration of a rotating twisted Timoshenko beams under axial loading using differential transform[J]. International Journal of Mechanical Science, 1999, 41(11): 1339-1356.
[10]王琳.输流管道的稳定性、分岔与混沌行为研究[D].武汉:华中科技大学,2006.
[11]Hosseini M, Sadeghi-Goughari M, Atashipour S A, et al. Vibration analysis of single-walled carbon nanotubes conveying nanoflow embedded in a viscoelastic medium using modified nonlocal beam model[J].Archives of Mechanics, 2014, 66(4): 217-244.
[责任编辑 尚 晶]
Vibration and instability of single-walled carbon nanotubes conveying fluid in a longitudinal magnetic field
LiMing,ZhouPanfeng,ZhengHuasheng
(Hubei Province Key Laboratory of Systems Science in Metallurgical Process, Wuhan University of Science and Technology, Wuhan 430065, China)
On the basis of nonlocal elastic theory and with the slip boundary conditions and small scale effect of nanotubes considered, this paper uses Euler-Bernoulli beam model to investigate the vibration and instability of a simply-supported single-walled carbon nanotube (SWCNT) conveying fluid in a longitudinal magnetic field. Transverse vibration equation and its boundary conditions of the SWCNT are derived according to Hamilton’s principle. Differential transformation method (DTM) is adopted to solve this high-order partial differential equation. Effects of magnetic field intensity, small scale parameter and Knudsen number on vibration frequency and stability of fluid-conveying SWCNT are analyzed by numerical calculation. The results show that with the increase of small scale parameter and Knudsen number, the fundamental frequency and critical flow velocity of the SWCNT decrease and the system’s stable region is reduced; when its intensity increases to a certain degree, the longitudinal magnetic field can obviously raise the fundamental frequency and critical flow velocity, i.e. enlarge the system’s stable region.
carbon nanotube; longitudinal magnetic field; fluid-conveying; differential transformation method; vibration; instability; critical flow velocity
2016-09-08
国家自然科学基金资助项目(51608401); 武汉科技大学冶金工业过程系统科学湖北省重点实验室开放基金资助项目(Y201520).
李 明(1969-),女,武汉科技大学副教授,博士. E-mail:mingli121212@126.com
10.3969/j.issn.1674-3644.2017.01.006
O353.1
A
1674-3644(2017)01-0027-05
