文化基因算法求解多工艺路线炼钢-连铸生产调度问题

李 玲，唐秋华，张利平

(武汉科技大学机械自动化学院，湖北 武汉，430081)

文化基因算法求解多工艺路线炼钢-连铸生产调度问题

李 玲，唐秋华，张利平

(武汉科技大学机械自动化学院，湖北 武汉，430081)

针对包含多工艺路线的炼钢-连铸生产调度问题，综合考虑生产过程中的多种约束条件，以文化基因算法为基础提出一种新的求解方法。在文化基因算法设计过程中，对于不同工艺路径的机器选择，采用启发式规则指导的机器指派方法；在算法优化中，通过引入基于连接矩阵的相似工件块交叉方法和基于基因位全插入的邻域搜索算子，从全局和局部搜索角度全面提高算法性能。最后，通过对多组算例进行对比分析，验证了本文算法的可行性和优越性。

炼钢-连铸；生产调度；文化基因算法；多工艺路线；启发式规则；邻域搜索

钢铁生产中的炼钢-连铸阶段操作过程复杂，工艺约束条件多，是生产调度的难点。在炼钢车间实际生产中，往往由于钢种不同而需要多种工艺路线混合作业，因此有必要针对该生产状况下的炼钢-连铸调度问题进行研究。

炼钢-连铸生产调度问题的研究方向可大致分为最优化方法、智能算法和启发式方法三类。Xuan等[1]和Mao等[2]分别建立了炼钢-连铸生产调度问题的整数规划模型，并基于拉格朗日松弛方法进行求解。叶云等[3]针对具有多缓冲的炼钢-连铸生产调度问题，建立了基于单元特定事件的连续时间混合整型线性规划模型并进行求解。李铁克等[4]以混合流水车间调度理论为基础研究炼钢-连铸调度问题，结合线性规划方法提出一种两阶段遗传算法。马文强等[5]建立了炼钢-连铸生产调度数学模型，并提出一种混合教与学优化算法进行求解。孙亮亮等[6]根据各浇次的铸机选择结果来构造浇次集合，设计了一种基于启发式规则的深度优先搜索算法进行连铸过程调度。

上述研究针对不同生产状况下的炼钢-连铸问题都提出了有效的调度方法。但是，除文献[5]以外，其余文献研究的都是确定的单一工艺路线条件下的炼钢-连铸调度。例如，在文献[1]、[4]、[6]中，加工工艺路线是炼钢-精炼-连铸；文献[2]中的工艺路线为炼钢-精炼(RH精炼+LF精炼)-连铸；文献[3]中的工艺路线是炼钢-精炼(AOD精炼+LF精炼)-连铸。上述文献研究的工艺路线具有单一性，即每个炉次所经过的加工工艺路线均相同。然而在实际生产中，由于订单日趋多样化，工艺路线混合生产逐渐成为常态，故各钢包的工艺路线可以有多种。

本文针对多工艺路线炼钢-连铸生产调度问题，以文化基因算法为基础，考虑不同工艺路线中机器选择的不同，采用启发式规则进行机器指派。另外，在算法设计中通过相似工件块单点交叉的方法更有效地保留精英个体中高性能的工件组合,并采用邻域搜索等方式来提高算法的优化性能。最后通过多组算例对该算法进行测试，并与遗传算法进行结果对比，以检验本文算法的有效性。

1 多工艺路线炼钢-连铸生产调度

1.1 工艺路线

鉴于炼钢和精炼工艺的多样性，不同炼钢厂的生产过程有所差异，本文研究的炼钢-连铸工艺过程源于武汉某钢铁公司，如图1所示，其工艺流程包括转炉炼钢(LD)、吹氩(AR)、钢包精炼处理(LF)、真空脱气(RH)、回转台吊装(CW)和连铸(CC)多个阶段，每个阶段又包含若干台具有相同处理能力的并行机。

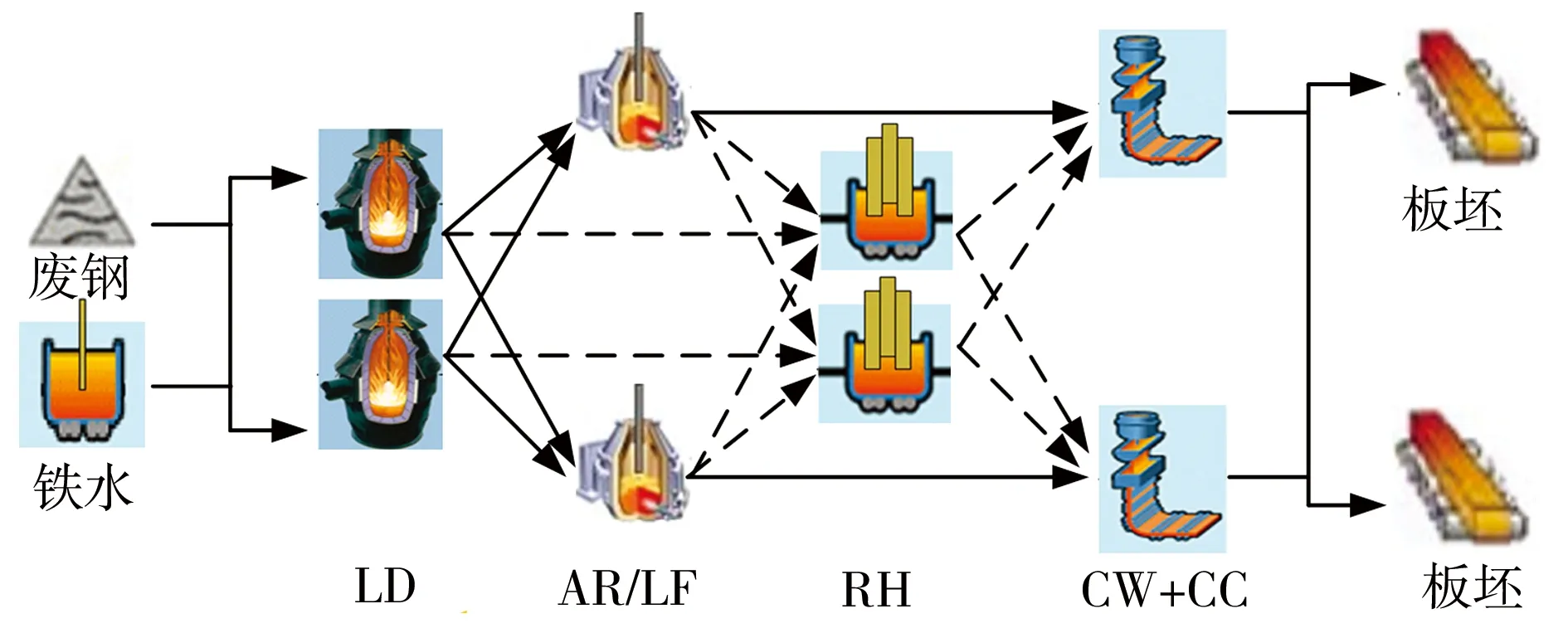
图1 炼钢-连铸多工艺路线流程示意图

由于钢种成分及规格要求存在差异，不同钢种的工艺路线可能不同，如重轨钢、帘线钢等品质要求较低的钢种，生产过程只需要经过LF或RH精炼，而如硅钢等高品质钢种，往往需要经过多重精炼。本文根据企业实际情况，考虑了4种常见的工艺路线，分别为LD-LF-CW-CC、LD-AR-CW-CC、LD-LF-RH-CW-CC和LD-RH-CW-CC。

1.2 炼钢-连铸生产调度

炼钢-连铸生产属于流水作业，必须满足流水作业车间调度的一般性约束。同时炼钢生产具有高温作业特性，因此各工序间需要连续加工。在连铸之前的工艺阶段，钢水以炉次为单位，通过钢水包经由天车进行转运，可在同一阶段任意机器上进行加工。在连铸阶段，由于铸机的工艺约束，通常要求若干炉成分相同或近似的炉次组成一个浇次。属于同一浇次的各炉次必须在同一台铸机上进行连浇连铸，即炼钢-连铸生产在最后阶段通常以浇次为单位实行批量化作业。

炼钢-连铸生产调度是在浇次任务(包括各浇次的炉次数)、设备状况已知的条件下，确定各炉次在各阶段的机器选择以及开始、结束时间，同时要满足前述各项约束。常见的生产调度目标主要包括最小化最大完工时间、最小化总完工时间、最小化机器等待时间、最大化设备利用率等。本文选取最小化最大完工时间作为优化目标。

2 算法设计

2.1 文化基因算法

文化基因算法[7](memetic algorithm，MA)是一种模拟社会文化进化的新型智能算法。该算法认为模拟生物进化机制的变异操作属于含有一定噪声的爬山搜索，在进化过程的众多变种中通过一次简单扰动来提高整体性能具有很大的盲目性。因此，在机理上文化基因算法认为变异过程需要大量“专业知识”支撑，在实际操作中则通过引入局部启发式搜索实现。

文化基因算法强调局部搜索算子的作用，能够结构性优化算法性能，因此在生产调度领域得到了大量应用。特别是在解决实际工程问题中，通过引入启发式规则指导搜索方向可以大大提高算法的性能和效率。针对具有多工艺路线的炼钢-连铸生产调度问题，本文以文化基因算法为基础进行求解，将炼钢-连铸调度问题的特性融入编码、解码过程和算子设计中，以保证算法的可行性。

2.2 针对炼钢-连铸调度问题的算法求解

多工艺路线条件下，由于不同浇次的生产路径不同，确定各任务的机器选择也变得更为复杂。以浇次为单位，根据算法生成的浇次顺序来依次确定各浇次内炉次的机器选择是最简单的思路，但这种方法在对当前浇次进行机器选择时没有有效信息作为参考，只能以贪婪的方式进行决策，而对后续浇次的决策不具有前瞻性。同时，在各阶段有并行设备的情况下，必然存在两个浇次在连铸前的设备中交错加工的情况，此时由于前一个浇次的分配已经确定，导致设备在未来的若干个时间区间上提前被占用，这就使得后续浇次的可行开浇时间难以确定。

本文采用文化基因算法，利用自然数编码方式产生浇次序列，结合倒推方法和启发式规则进行解码，并根据问题特性，采用基于相似工件块的单点交叉方法和局部搜索算子进行优化求解。

2.3 面向混合流水作业的编码与解码

在多工艺路线混合的生产条件下，不同浇次的阶段数不同，机器选择情况复杂，故先通过算法确定各浇次的开浇时间顺序，再通过启发式规则实现解码。

编码：由于算法只用于确定浇次顺序，故采用基本的自然数编码方式，基因位顺序即为浇次顺序，基因位上的值即为该位置的浇次编号。

解码：为满足各浇次在铸机上的连续浇铸约束，本文采用倒推的方法，以浇次序列的逆序作为各浇次开浇时间的顺序，利用最早可用机器优先规则将其安排在铸机上；然后以炉次为单位，同时采用最早完工时间优先规则和最早可用机器优先规则，将各炉次任务以倒排的方法分配在铸机前的各个工序上；最后按正常工艺顺序将整个调度的计划时间进行翻转，得到可行的调度计划表。

2.4 面向多工艺路线的全局搜索算子

选择操作：由于本研究的优化目标为最小化问题，故选取最大完工时间的倒数作为适应度函数值f，以轮盘赌方式进行选择。

交叉操作：由于工艺路线的多样性，浇次之间的组合必然在很大程度上影响着整个生产计划的最大完工时间。研究表明[8]，在种群进化过程中会逐步形成许多高性能的工件组合，称为工件块，这些工件块可能出现在不同染色体的同一位置或不同位置。因此，保留高性能染色体上重复出现的工件组合能更好地保留较优染色体的有用信息，有助于整个种群的进化。如果交叉操作破坏了这些工件块，生成低劣后代染色体的可能性就较大。

本文采用一种相似工件块单点交叉(similar block one-point crossover, SBOPX)的方法，首先从当前种群中选出一定比例的精英个体，并从这些精英染色体中提取工件块信息。记Λ=[λj′,j]m×m为工件的连接矩阵，其中λj′,j表示在精英染色体中工件对(j′,j)出现的次数。初始时令Λ=[0]m×m，逐步扫描每一个精英个体，扫描结束后如果λj′,j>1，就称工件对(j′,j)为工件块。

例如，有3个精英个体分别为：

π1={3,4,7,5,2,8,6,9,1} ，

π2={2,1,3,4,5,6,9,8,7},

π3={6,3,2,1,9,8,7,5,4},

可计算得到工件的连接矩阵如表1所示。

表1 连接矩阵

基于连接矩阵，SBOPX的操作步骤如下，结果如图2所示。

(1)根据连接矩阵查找父代染色体上的工件块，直接把它们复制到相应子代染色体的相同位置上。

(2)随机产生一个交叉点。

(3)复制父代染色体1位于交叉点之前的部分到子代染色体1的相同位置上，将子代染色体1缺失的工件从父代染色体2上依次复制到空余位置。

(4)复制父代染色体2位于交叉点之前的部分到子代染色体2的相同位置上，将子代染色体2缺失的工件从父代染色体1上依次复制到空余位置。

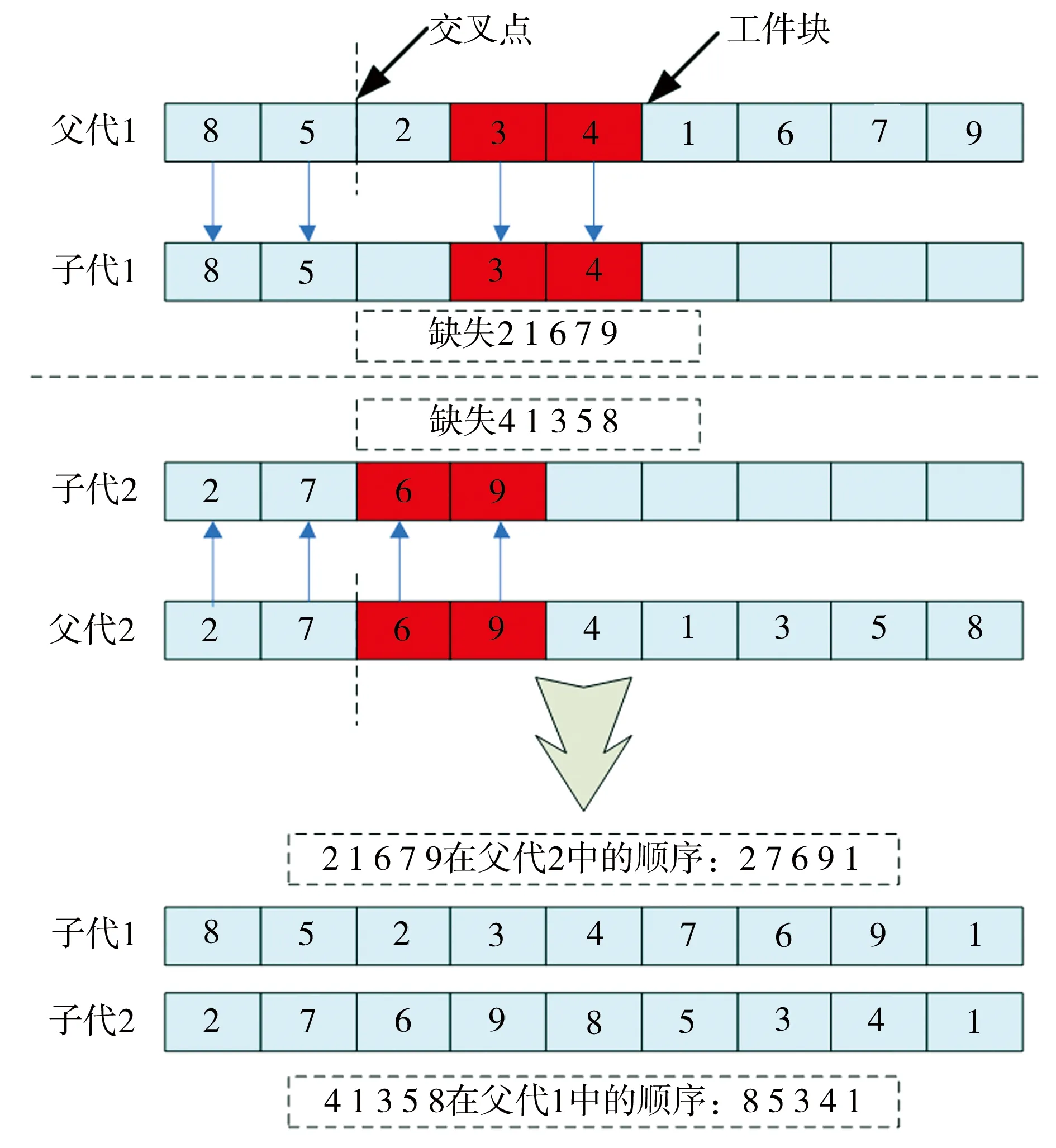
图2 SBOPX的操作过程

2.5 面向多工艺路线的局部搜索算子

多工艺路线混合生产条件下，机器使用情况呈现出很强的无规律性，通过传统调度方法和经验方法都难以制定出高效的调度方案。在文化基因算法设计中，通过采用基因位全插入的大规模局部搜索算法系统地优化邻域结构，提高设备利用率，同时有效防止算法陷入局部最优。局部搜索过程如下：

(1)令i=1:PS(PS为种群规模)，对每一条染色体生成全局搜索后的一个初始解π。

(2)令n=1(n为局部搜索次数)。

(3)随机从π中无重复地抽取一个工件，将该工件分别插入到π的所有位置(原位置除外)。评价所得到的排列，令π′为其中最好的排列。

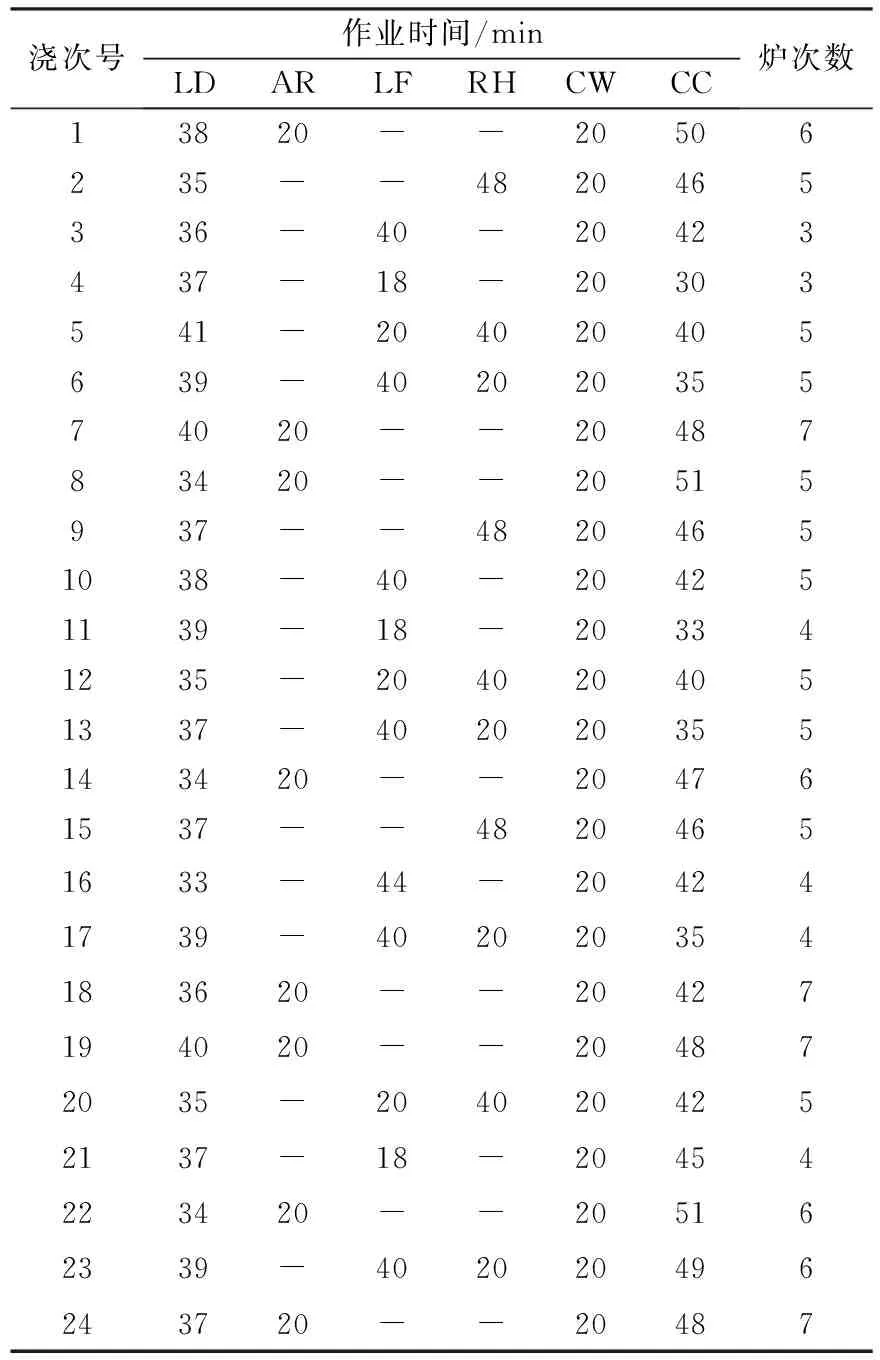
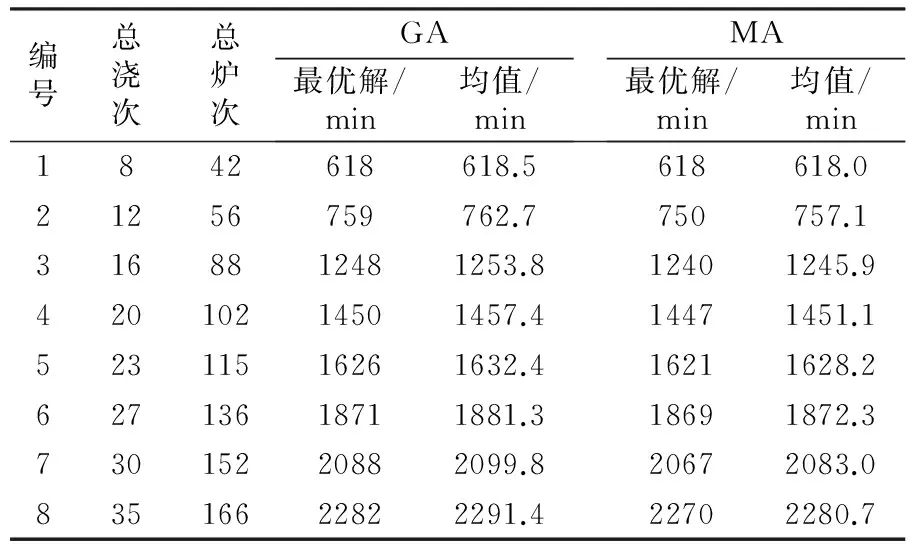
(4)若f(π′)

2.6 算法伪代码

//初始化

定义邻域搜索次数N；

种群大小PS；

最大浇次数CAST_NUM；

fori=1 toPSdo

随机生成所有染色体；

end for

while (计算时间未满足终止条件) do

//计算适应度函数

fori=1 toPSdo

Fitness(i)=Fitfun(Parent(i));

end for

Population=Sort(Parent(i)); //将种群按适应度值降序排列

//全局搜索算子

fori=1 toPSdo

Parent(i)=Roulette Selection(Population);//轮盘赌选择

end for

for(j=1;j

(Offspring(j),Offspring(j+1))=SBOPX(Parent(i)，Parent(i+1));//交叉

end for

//局部搜索算子

定义π为全局搜索后的染色体，作为邻域搜索的初始解；

fori=1 toPS

n=1;//局部搜索次数

while(n

随机选择一个工作(没有重复)；

π′=Neighborhood search(π);//对初始解进行邻域搜索

if Fitness(π′)

then break;//跳出循环

elsen=n+1;

end while

end for

Population=Sort(Offspring);//更新原种群

end while

3 算法测试与结果分析

为了验证所提出算法的性能，分别采用实际生产数据和随机模拟生成的数据进行测试计算，并与遗传算法的计算结果进行比较。遗传算法(GA)是智能算法领域最为经典也最为有效的算法之一，在流水车间调度中得到了广泛应用。本文作为对比实验的遗传算法是根据文献[9]中遗传算法的结构进行设计的，在该遗传算法的基础上，对交叉策略又进行了相应改进。所有算法均采用C语言编程，程序运行环境为CPU 3.00 GHz，内存为2 GB。

3.1 参数设置

由于算法性能受参数影响较大，故需要通过多因素方差分析确定最优的参数组合。对于文化基因算法，共考虑种群规模、交叉概率、精英个体比例三个参数，其中种群规模设置(20,40,60)三个水平，交叉概率设置(0.7,0.8,0.9)三个水平，精英个体比例设置(0.2,0.5,0.8)三个水平。设计正交试验，对每个参数组合单独运行10次，取其平均值作为最终结果，然后用SPSS软件对所求结果进行方差分析。结果表明，对目标函数的影响程度上，种群规模>交叉概率>精英个体比例，最终选取的目标水平如下：种群规模为60，交叉概率为0.9，精英个体比例为0.8。

为保证对比实验的公平性，遗传算法进行同样的参数选择。对遗传算法，考虑种群规模、交叉概率和变异概率三个参数，前两个因素水平设置同上，变异概率取(0.05,0.1,0.2)三个水平，经多因素方差分析，得到最佳的因素水平组合：种群规模为40，交叉概率为0.7，变异概率为0.1。

3.2 实际生产数据测试结果与分析

本文所采用的实际生产数据参照文献[5]，如表2所示，测试结果如表3所示。

表2 实例数据

表3 实例测试结果

由表3可以看到，文化基因算法获得的最优解要好于遗传算法获得的最优解。同时，与文献[5]中算法获得的最优解(1976 min)相比，文化基因算法获得的结果优化了5.72%，可见本文算法中基于问题属性设计的解码方式及算子结构有效提升了算法性能。

3.3 随机生成数据测试结果与分析

为了进一步验证文化基因算法的有效性，本文随机生成规模不同的若干组数据进行测试。浇次数在(5,40)之间随机产生，共生成8组案例，每个浇次的炉次数在(3,7)之间随机产生，各工序的加工时间根据实际情况在合理范围内随机产生。为保证算法对比的公平性，参照文献[10]，各算法均采用计算时间t为终止条件：t=200p(q/2) ms，其中p为任务数、q为机器数。计算结果如表4所示。

表4 随机生成数据测试结果

由表4可见，虽然对于小规模案例，GA和MA两种算法都能得到相同最优解，但随着问题规模的增大，MA所得最优解及均值都要好于GA计算结果。总之，在相同的计算时间内，文化基因算法明显改进了解的质量，其性能优于遗传算法。

4 结语

本文针对具有多工艺路线的炼钢-连铸生产调度问题，设计了一种高效的文化基因算法。该算法考虑实际问题特性，引入基于工件连接矩阵的相似工件块单点交叉方法和以基因位全插入操作为核心的局部搜索方法，有效提高了算法性能。通过设计不同规模的测试算例，并与遗传算法进行结果对比，验证了本文算法的可行性和高效性。

[1] Xuan Hua, Tang Lixin. Scheduling a hybrid flowshop with batch production at the last stage[J]. Computers and Operations Research,2007,34(9):2718-2733.

[2] Mao Kun, Pan Quanke, Pang Xinfu, et al. A novel Lagrangian relaxation approach for a hybrid flowshop scheduling problem in the steelmaking-continuous casting process[J]. European Journal of Operational Research, 2014, 236(1):51-60.

[3] 叶云, 唐秋华, 易磊, 等. 基于单元特定事件的多缓冲炼钢连铸生产调度建模[J].武汉科技大学学报， 2013,36(2):104-107.

[4] 李铁克,苏志雄. 炼钢连铸生产调度问题的两阶段遗传算法[J]. 中国管理科学,2009,17(5):68-74.

[5] 马文强,张超勇,唐秋华,等. 基于混合教与学优化算法的炼钢连铸调度[J]. 计算机集成制造系统,2015,21(5):1271-1278.

[6] 孙亮亮,刘炜,柴天佑. 基于深度优先搜索算法的连铸过程调度方法的研究[J].控制理论与应用, 2010,27(12):1705-1710.

[7] Moscato P. An introduction to population approaches for optimization and hierarchical objective functions: a discussion on the role of tabu search[J]. Annals of Operations Research, 1993,41(2):85-121.

[8] Ruiz R, Maroto C, Alcaraz J. Two new robust genetic algorithms for the flowshop scheduling problem[J]. Omega, 2006,34(5):461-476.

[9] 秦艳. 改进交叉策略的GA在流水车间多目标调度中的应用[J]. 现代制造工程,2010(12):29-32.

[10]Pan Quanke, Ruiz R. An estimation of distribution algorithm for lot-streaming flow shop problems with setup times[J]. Omega, 2012,40(2):166-180.

[责任编辑 尚 晶]

Memetic algorithm for steelmaking-continuous casting production scheduling
with multiple process routes

LiLing,TangQiuhua,ZhangLiping

(College of Machinery and Automation, Wuhan University of Science and Technology, Wuhan 430081, China)

On the basis of memetic algorithm, a new method considering the multiple constrains in production is put forward to solve the scheduling problem of steelmaking-continuous casting production with multiple process routes. During the design of memetic algorithm, the heuristic rules guided assignment method is used to choose the machine for different process routes. Then the similar block one-point crossover operator based on the connection matrix and the neighborhood search operator based on a fully inserted method are adopted to improve the performance of global and local searching. Finally, contrastive analysis of several cases verifies the feasibility and superiority of the proposed algorithm.

steelmaking-continuous casting; production scheduling; memetic algorithm; multiple process route; heuristic rule; neighborhood search

2016-09-29

国家自然科学基金资助项目(51275366,51305311)；高等学校博士学科点专项科研基金课题(博导类)(2013421911002)；中国博士后科学基金资助项目(2013M542073).

李 玲(1991-)，女，武汉科技大学硕士生.E-mail: 1299105704@qq.com

唐秋华(1970-)，女，武汉科技大学教授，博士生导师.E-mail: tangqiuhua@wust.edu.cn

10.3969/j.issn.1674-3644.2017.01.004

TF087；TP29

A

1674-3644(2017)01-0017-06