一种用于条纹相机图像的多尺度小波边缘检测算法

李阳,彭博栋,盛亮,黑东炜,李奎念,张美,赵吉祯

(1.西安交通大学电气工程学院，西安710049;2.西北核技术研究所，西安710024; 3.强脉冲辐射环境模拟与效应国家重点实验室，西安710024)

一种用于条纹相机图像的多尺度小波边缘检测算法

李阳1,2,3,彭博栋2,3,盛亮2,3,黑东炜2,3,李奎念2,3,张美1,2,3,赵吉祯2,3

(1.西安交通大学电气工程学院，西安710049;2.西北核技术研究所，西安710024; 3.强脉冲辐射环境模拟与效应国家重点实验室，西安710024)

针对条纹相机图像特点，通过对多尺度小波边缘检测算法的核函数进行特定方向的拉伸，抑制电磁干扰等因素造成的伪边缘，构造了一种对条纹相机图像空间轴方向灵敏的边缘检测算子，并利用数据融合方法，使该算法同时具有较大和较小2种不同尺度下小波边缘检测的优点。数值实验证明，该算法在用于条纹相机图像边缘检测时，边缘定位较为准确，产生的伪边缘少，不易受噪声干扰。

条纹相机；图像处理；边缘检测；小波边缘检测算法；多尺度

灰度图像边缘，一般指图像中灰度发生急剧变化的边界区域。根据灰度的变化趋势，通常将边缘划分为阶跃状和屋顶状2种类型。阶跃状边缘两边的灰度值有较大差异，而屋顶状边缘位于灰度值增加与减少的交界处。图像的很大一部分信息存在于边缘中，因此，边缘检测在图像处理中占有重要地位，是计算机视觉、机器智能等领域研究的经典课题之一，其检测结果的准确性直接影响智能系统对客观世界的理解与判断。

条纹相机成像与普通相机不同，其工作原理如图1(a)所示。条纹相机通过镜头和一条狭缝将待测目标的一部分(狭缝所对的部分)成像在光阴极上，光阴极受激产生的光电子经倍增后在电荷耦合器件(charge-coupled device, CCD)上成像，这样，单独一幅图像是一条狭长的“条纹”。扫描电路控制光阴极产生的电子沿垂直于狭缝的方向“扫过”，在CCD上形成一幅图像，因此，条纹相机图像相当于若干一维图像的“拼合”，边缘信息主要集中在平行于狭缝的方向(列)上，垂直于狭缝的方向(行)相当于时间轴。图1(b)为某次平面丝阵Z箍缩实验的条纹相机图像[1]，其垂直方向为空间轴，水平方向为时间轴，容易看出该图像具有明显的“条纹相机特征”[2]。

基于条纹相机的图像特征，准确获得每列像素的边缘可以给出待测目标某一“切片”的边缘随时间的变化情况。然而，受扫描非线性和电磁干扰等因素影响，条纹相机图像中经常出现一些纵向条纹，这些条纹在边缘检测中很容易被误判为边缘，即产生伪边缘。

当前，主流的边缘检测算法是通过一个预设的滤波器对图像进行滤波，得到滤波图像，并根据滤波图像每个像素的灰度值，判断该像素是否为边缘点。通常，预设的滤波器对图像灰度值变化较为敏感，若某像素周围的灰度值变化剧烈，滤波后对应位置输出的灰度值会更大。所以边缘检测算法一般会将某邻域中灰度梯度最大的像素点判定为边缘。边缘检测算法主要有Roberts算法、Prewitt算法、Sobel算法、LOG算法和Canny算法等。Roberts算法和Prewitt算法依据任意一对互相垂直的差分算子可计算梯度的原理，利用灰度一阶差分进行边缘判断。Sobel算法计算梯度的原理与Roberts算法相似，它进一步对参考像素的邻域像素作加权分析，所以对噪声具有一定的平滑作用。LOG算法[3]对二阶微分Laplacian算子进行了改进，形成了LOG算子。该算子先用高斯函数对图像进行平滑滤波，再利用差分算子检测相应尺度上的边缘。数学上已经证明，LOG算子是根据二阶导数0交叉点检测阶跃型边缘的最佳算子。Canny算法[4-5]是目前边缘检测算法中公认效果较好的算法，其基本思想是先将待检测图像用高斯函数进行平滑，再由一阶微分的极大值确定边缘点。Mallat基于Canny边缘检测算法和小波变换原理提出多尺度边缘检测算法[6]，利用小波变换的特点，在不同尺度上对图像进行边缘检测，取得更佳的边缘定位效果。随着数字图像像素点尺寸越来越小，边缘处相邻像素灰度值的差异也越来越小，这限制了以梯度为主要判断依据的边缘检测算法。国内外学者还提出了一些其他的边缘检测算法，主要有基于模糊推理的边缘检测算法[7]、神经网络法[8]和遗传算法等。本文结合条纹相机图像特点，利用数据融合技术，对多尺度小波边缘检测算法进行了改进。

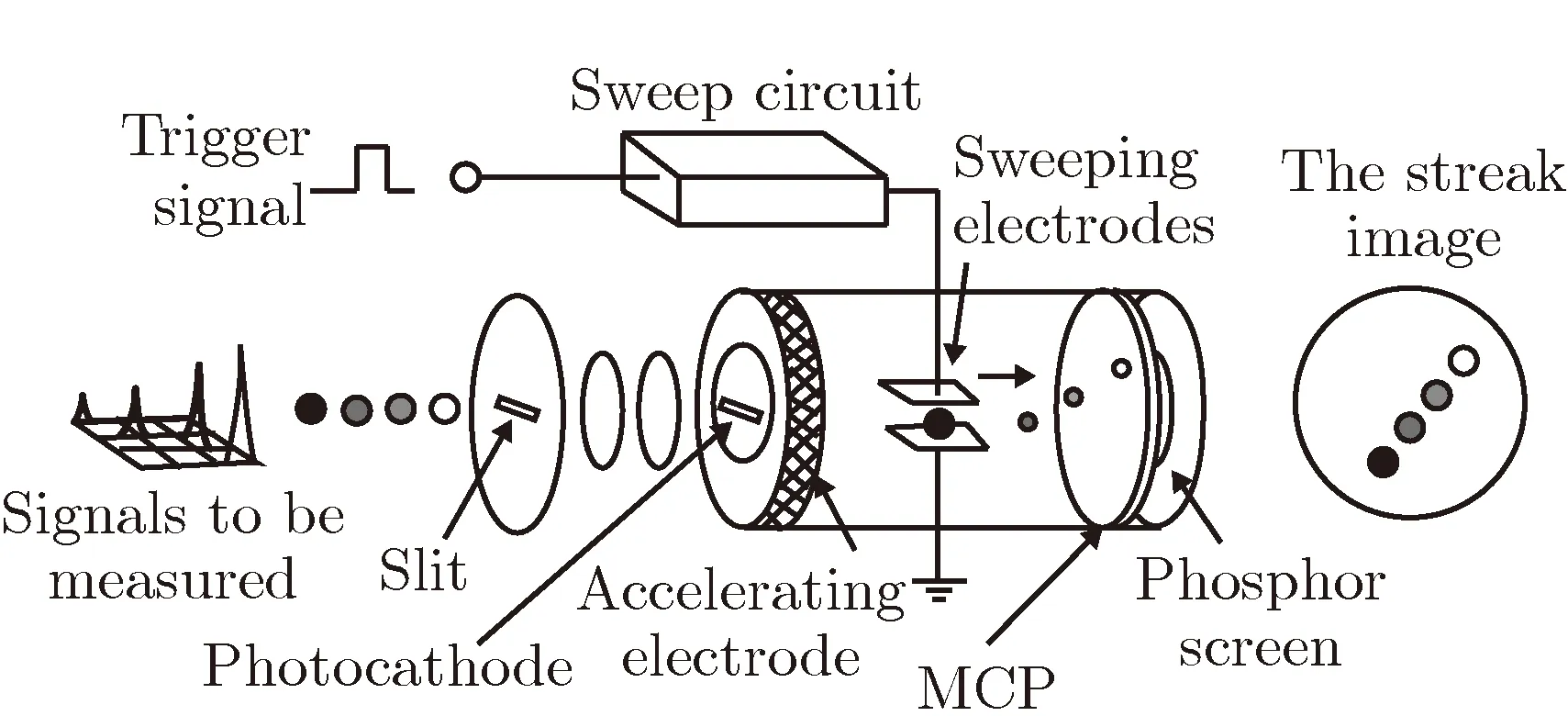
(a)Principle of streak camera

(b)A streak image of planar wire arrayin Z-pinch experiment

1 多尺度小波边缘检测算法

由Mallat提出的小波边缘检测算子是一种基于Canny算子的多尺度边缘检测方法[6,9]，基本思想是先用一个核函数的伸缩对图像进行卷积磨光，然后使用Canny边缘检测算法进行计算。计算中，核函数一般选为墨西哥草帽小波，即二维高斯函数θ(x1,x2)的2个一阶偏导数。

将2个小波函数记为

(1)

式中，σ为所用高斯函数的标准差；1≤k≤2。为便于计算和存储，取尺度为二进序列{2j}j∈Z。不同尺度下的小波函数可记为

(2)

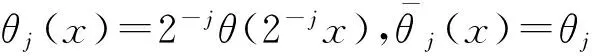
(3)

将待测图像用函数f表示，对上标k标记的2个方向有f∈L2(R2)。综合式(2)和式(3)，f在u点的二进小波变换为

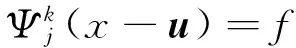
(4)

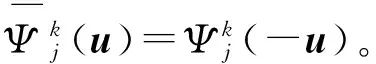
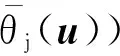
(5)

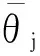
M(f(u,2j))=

(6)

式中，M(u)表示对向量u求模。

小波多尺度边缘检测算法的主要步骤为：在尺度2j下对f进行小波变换，并求出不同点的小波变换模；求出小波变换模矩阵的局部极大值点；通过非极大值抑制、边缘连接等方法获得该尺度下的图像边缘。

2 核函数伸缩

根据条纹相机图像特点，垂直方向灰度变化往往表示所拍摄物体的边缘，而水平方向灰度的变化可能是所拍摄物体的边缘，也可能是由于扫描电压非线性等原因产生的“纵向条纹”。物体边缘产生的灰度变化往往比较锐利，而纵向条纹变化较为平缓，并且在较大范围内灰度平均值与正常扫描值相同。这表明在进行水平方向边缘检测时，可以将核函数拉伸到更大的尺度，通过对大范围像素滤波，减少“纵向条纹”产生的伪边缘。本文选用的二维小波核函数如图2所示。

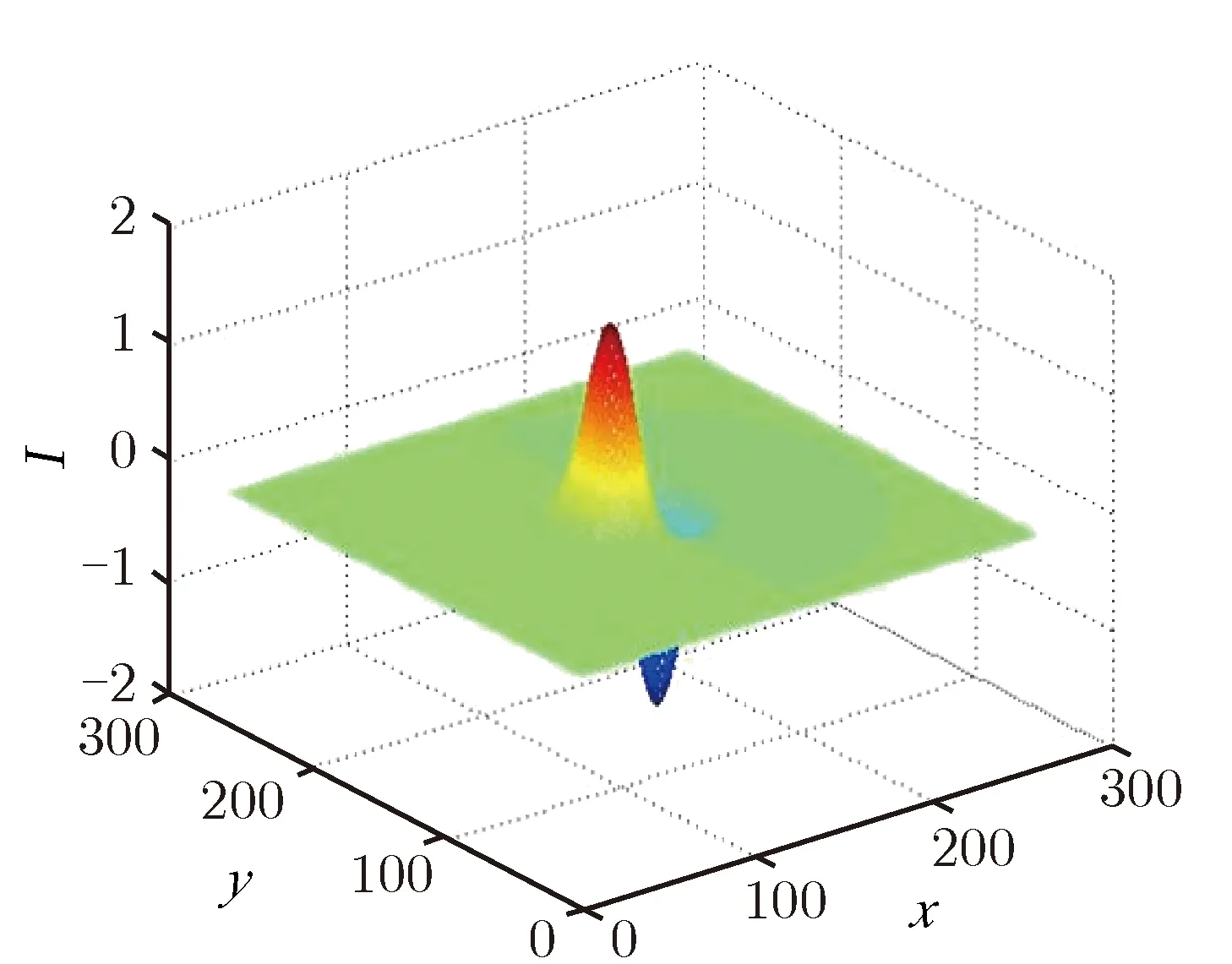
(a)x direction

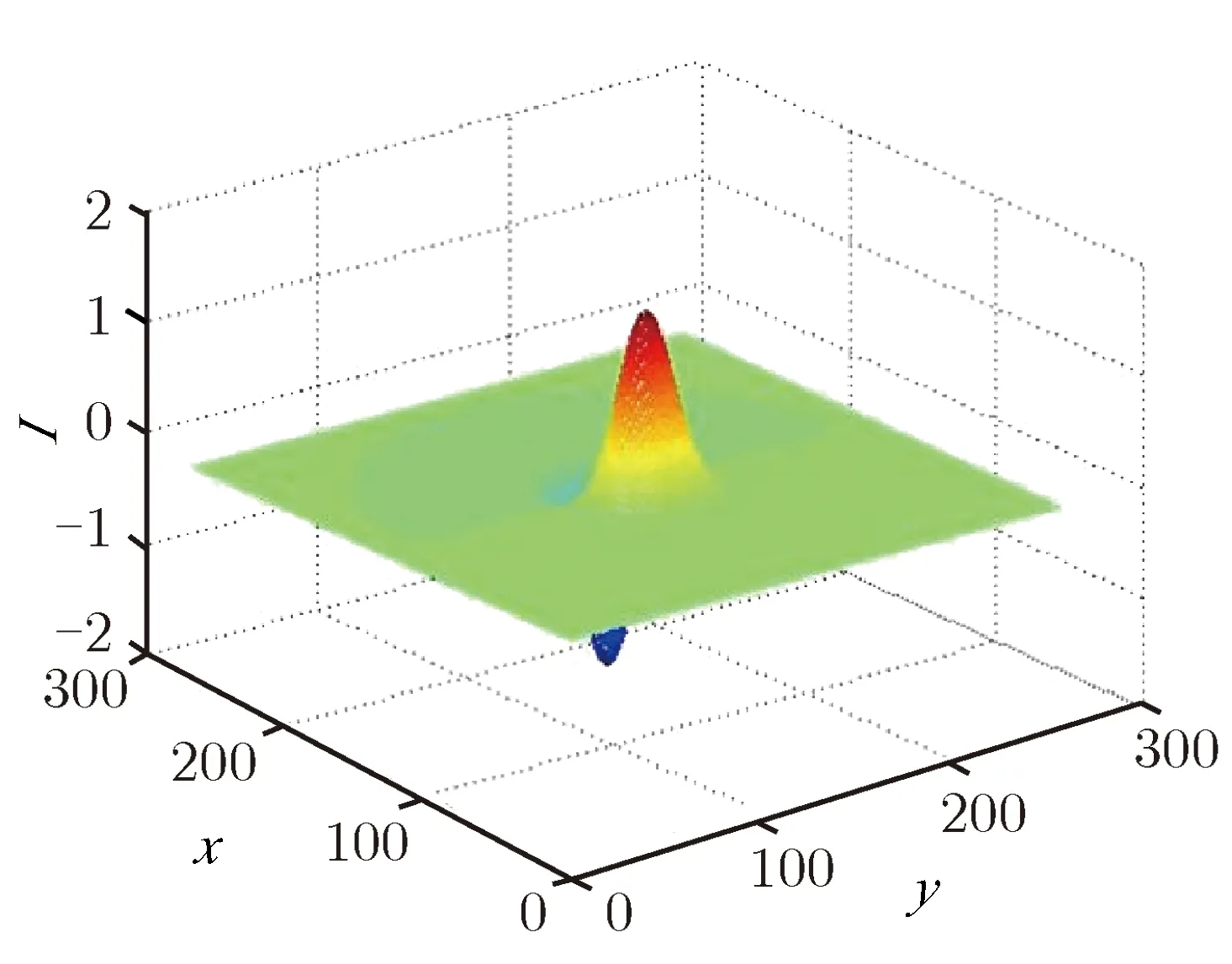
(b)y direction

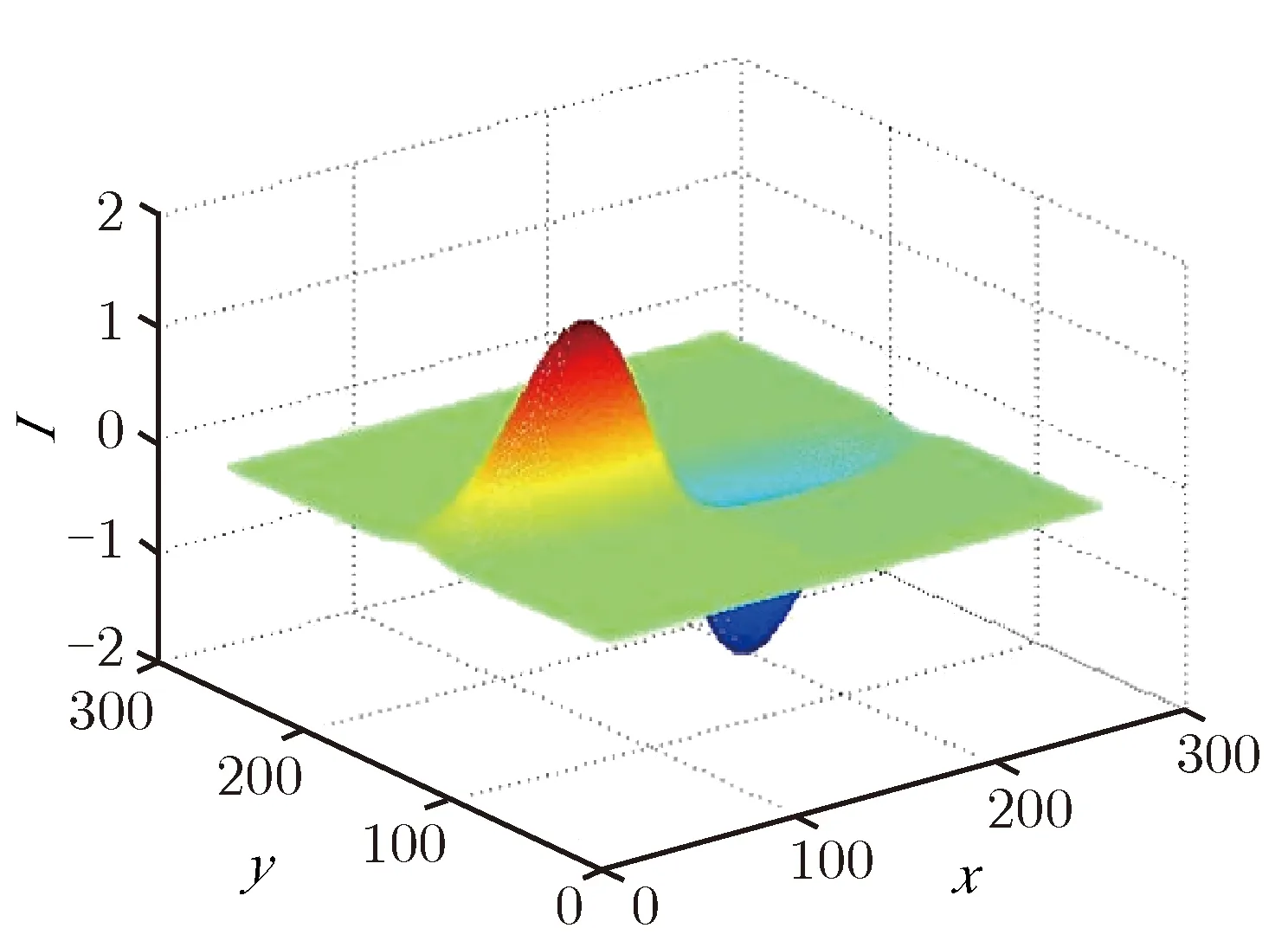
(c) Twice dilation of (a) along x

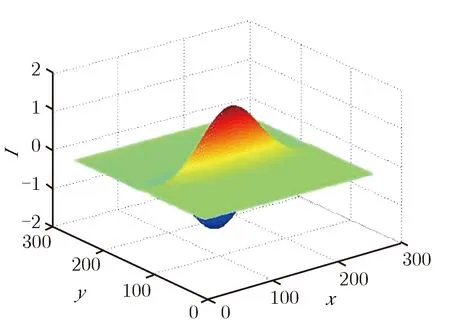
(d)Twice dilation of (b) along x

图2 像在不同的拉伸核函数下本文所用二维小波核函数
Fig.2Kernel functions used in the proposed edge detection algorithm

为形象地说明核函数拉伸的作用，图3给出了含噪分辨率卡图像在不同拉伸核函数下的边缘检测结果。其中，图3(a)为生成的含噪分辨率卡图像，使用拉伸后的核函数对该图片进行边缘检测；图3(b)为核函数不作任何变换时小波边缘检测算法的检测结果，图3(c)和图3(d)分别为沿水平方向拉伸3倍、5倍的检测结果。比较图3(b)、图3(c)和图3(d)可以看出，垂直方向的边缘检测分辨率基本保持不变，而随着对核函数的拉伸，水平方向边缘检测分辨率越来越差。核函数不拉伸时，可以分辨距离为4像素的边缘条纹；但当核函数拉伸为原来的3倍和5倍时，分别能分辨距离为16像素和32像素的条纹。核函数在某方向拉伸，抑制伪边缘的同时必然带来该方向边缘信息的损失，因此，需要合理控制拉伸倍数，以实现二者之间的平衡。由于条纹相机图像中纵向条纹宽度约为10像素，所以核函数沿水平方向拉伸3倍是一个既能抑制“纵向条纹”，又不会造成太多纵向边缘损失的选择。

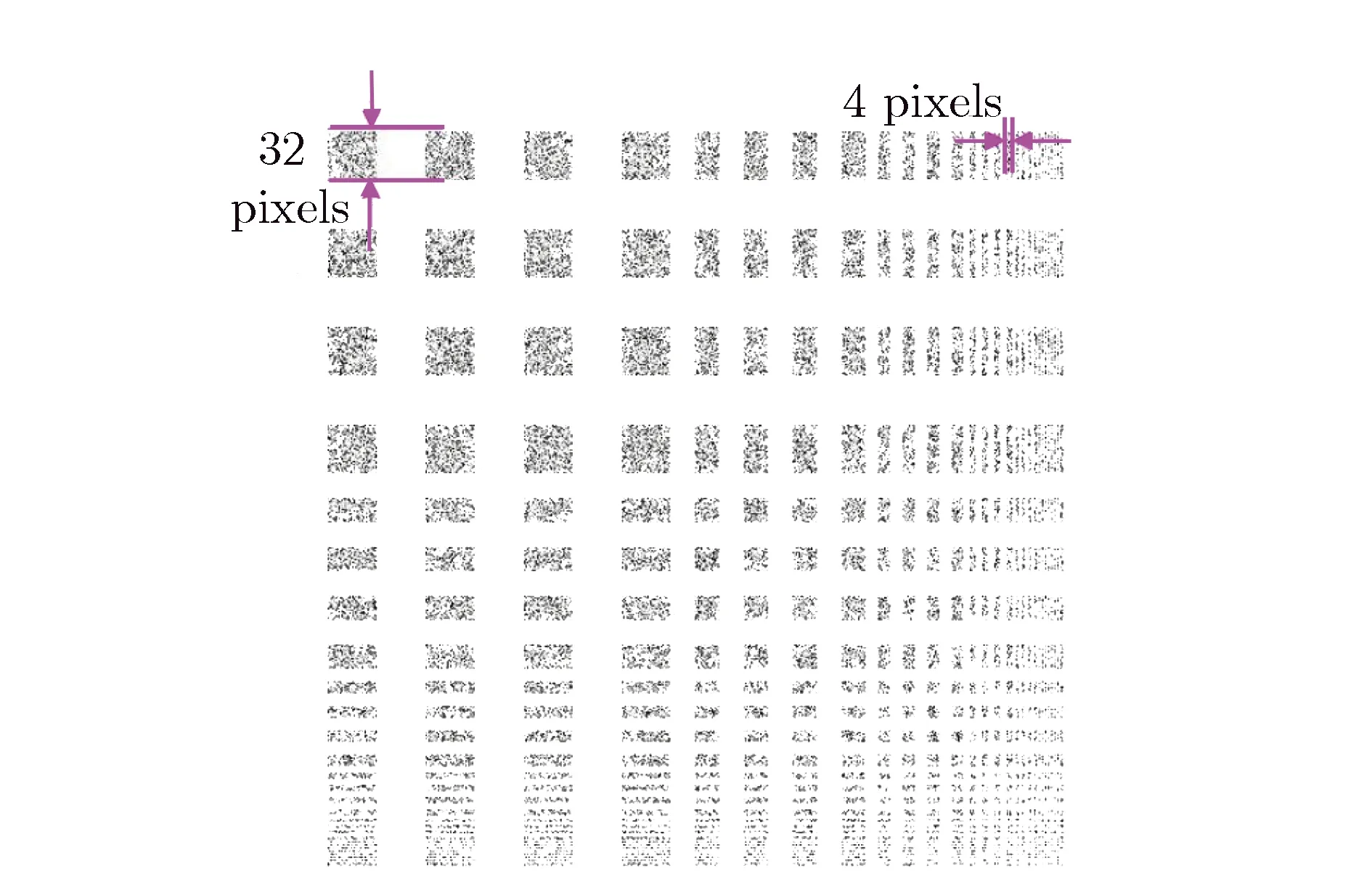
(a)Simulated nosiy image of a resolution chart

(b)Edge detected by original kernel function

(c)Edge detected by 3 times horizontal dilated kernel function

(d)Edge detected by 5 times horizontal dilated kernel function

图3 含噪分辨率卡图像在不同的拉伸核函数下的边缘检测结果
Fig.3A resolution charter generated by computer with white noise added and edge detection results with dilated kernel functions

为进一步说明本文算法和核函数拉伸的作用，图4给出了核函数沿水平方向拉伸3倍前后对图1(b)边缘检测的结果。从图4(a)和图4(b)可以看出，纵向条纹产生的伪边缘明显得到了抑制，但也丢失了一些细节信息，比如，图像早期融合前金属丝的边缘提取不够连续，程序判断的金属丝发光起始位置同拉伸前相比也存在几个像素的差异，如图4(c)所示。

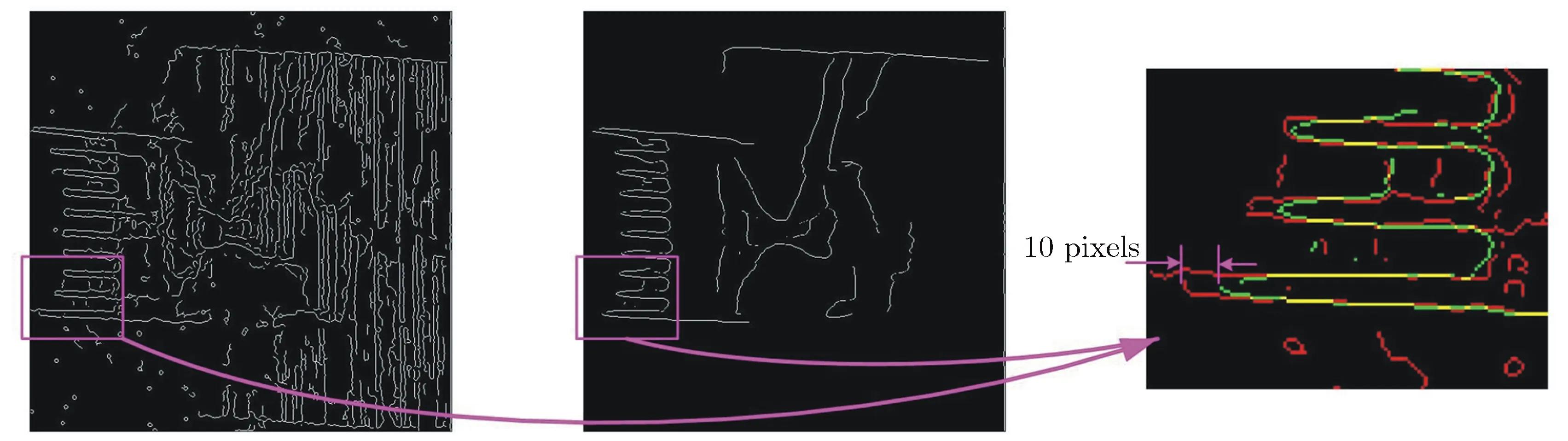
(a)Edge detected by original (b)Edge detected by 3 times dilated (c)Partial comparison kernel function kernel function in horizon of (a) and (b)

图4核函数水平方向拉伸3倍前后小波边缘检测效果比较
Fig.4Comparison of wavelet edge detection algorithm with different dilated kernel functions

3 尺度间数据融合

由上节讨论可知：当尺度较大时，检测结果不容易被噪声等干扰，但容易遗漏细节信息；当尺度较小时，边缘定位更为精确，含有更多的细节信息，但更容易产生伪边缘。如果能够结合不同尺度下边缘检测的优点，则可以得到更精准的边缘信息。小波边缘检测算法借助图像小波变换模M(f)判断某像素是否为边缘，将2个不同尺度下的小波变换模相乘，得到新的矩阵Mm(f)，对该矩阵进行极大值定位和边缘连接，得到的结果具有不同尺度下边缘检测的优点[10]。与文献[10]中的算法不同，本文仍然利用Canny提出的双阈值算法进行非极大值抑制。

利用含噪分辨率卡图像(图3(a))具有确定的边缘的特点，可以利用Pratt提出的品质因子[11]对不同算法的边缘检测结果进行客观对比。需要指出的是，因为图3(a)不具有条纹相机图像的独有特征，所以，对其处理的算法中，核函数没有进行水平方向的拉伸，而是使用正常二维高斯函数的一阶偏导数，见式(1)。

品质因子的定义为

(7)

式中，NI表示实际边缘的像素数目；NA表示探测到边缘的像素数目；d(k)表示第k个探测到的边缘像素与对应实际边缘之间的距离；α为用于惩罚错误边缘的设计常数，本文采用Pratt的设定，即α=1/9。F越大，表示边缘检测效果越好。

由于图3(a)噪声水平较高，所以Canny算法中使用了较高的边缘判断阈值(0.8)，以抑制由噪声造成的伪边缘。数值实验结果表明，对融合后矩阵进行非极大值抑制时，选取略小的阈值会取得更好的边缘检测效果。不同方法对图3(a)检测结果的比较，如图5所示。其中，图5(a)为实际边缘，图5(b)为Canny算法检测结果，图5(c)为较大尺度下小波边缘检测结果，图5(d)为较小尺度下小波边缘检测结果，图5(e)为不同尺度融合后的边缘检测结果，图5(f)为图5(c)与图5(e)的对比图。计算中，尺度系数相差0.5。可以看出，在较大尺度下，可以分辨距离为8像素的边缘，同时伪边缘较少；在较小尺度下，可以分辨距离为4像素的边缘，但是产生了较多的伪边缘。比较图5(c)、图5(d)、图5(e)和图5(f)可以看出，融合算法产生的伪边缘明显减少，同时具有较高的边缘分辨能力。

计算得到图5(b)、图5(c)、图5(d)和图5(e)的品质因子分别为0.141 7，0.521 6，0.669 9，0.566 4。由此可以看出，较小尺度下小波算法得到的边缘品质因子最高，但实际上与图5(c)和图5(e)相比，图5(d)明显含有更多伪边缘，检测效果并不是最好的。这是因为在品质因子的表达式中，存在伪边缘惩罚项1/max(NI,NA)，产生伪边缘会导致品质因数降低。但本文所用的例图中，实际边缘像素数NI=25 595，远大于检测出的边缘像素数NA(图5(c)：NA=12 348；图5(d)：NA=20 290；图5(e)：NA=13 466)。出现伪边缘对品质因子的影响被更大的实际像素数“遮掩”，因此造成图5(d)的品质因子更高。在边缘密集的图像中，如果边缘检测算法得到边缘数与实际边缘数相比低很多，应适当提升式(7)中惩罚伪边缘项的权重，才能准确反映边缘检测质量。

此外，分别使用较小尺度(j=0.5)和较大尺度(j=1)以及融合后算法对图1(b)进行边缘检测，结果如图6所示。从图中容易看出，融合边缘检测结果具有较小尺度边缘检测细节信息较多和较大尺度边缘检测伪边缘较少的优点。

(a)The actual edges (b)Canny edge

(c)Larger scale edges (d)Smaller scale edges

(e)Fusion edges (f)Comparison of (c) and (e)

图5 不同方法对图3(a)检测结果的比较
Fig.5Comparison of edge detection results of Fig.3 (a) with different algorithms

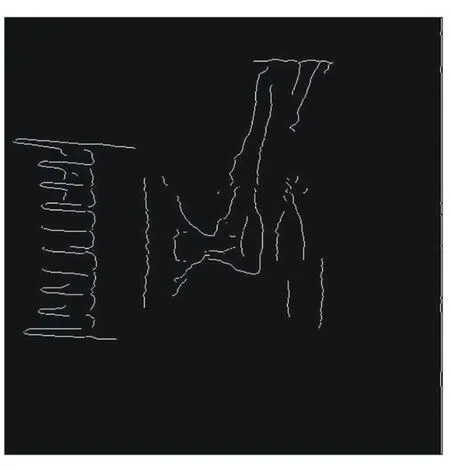
(a)Smaller scale(j=0.5) (b)Larger scale(j=1)

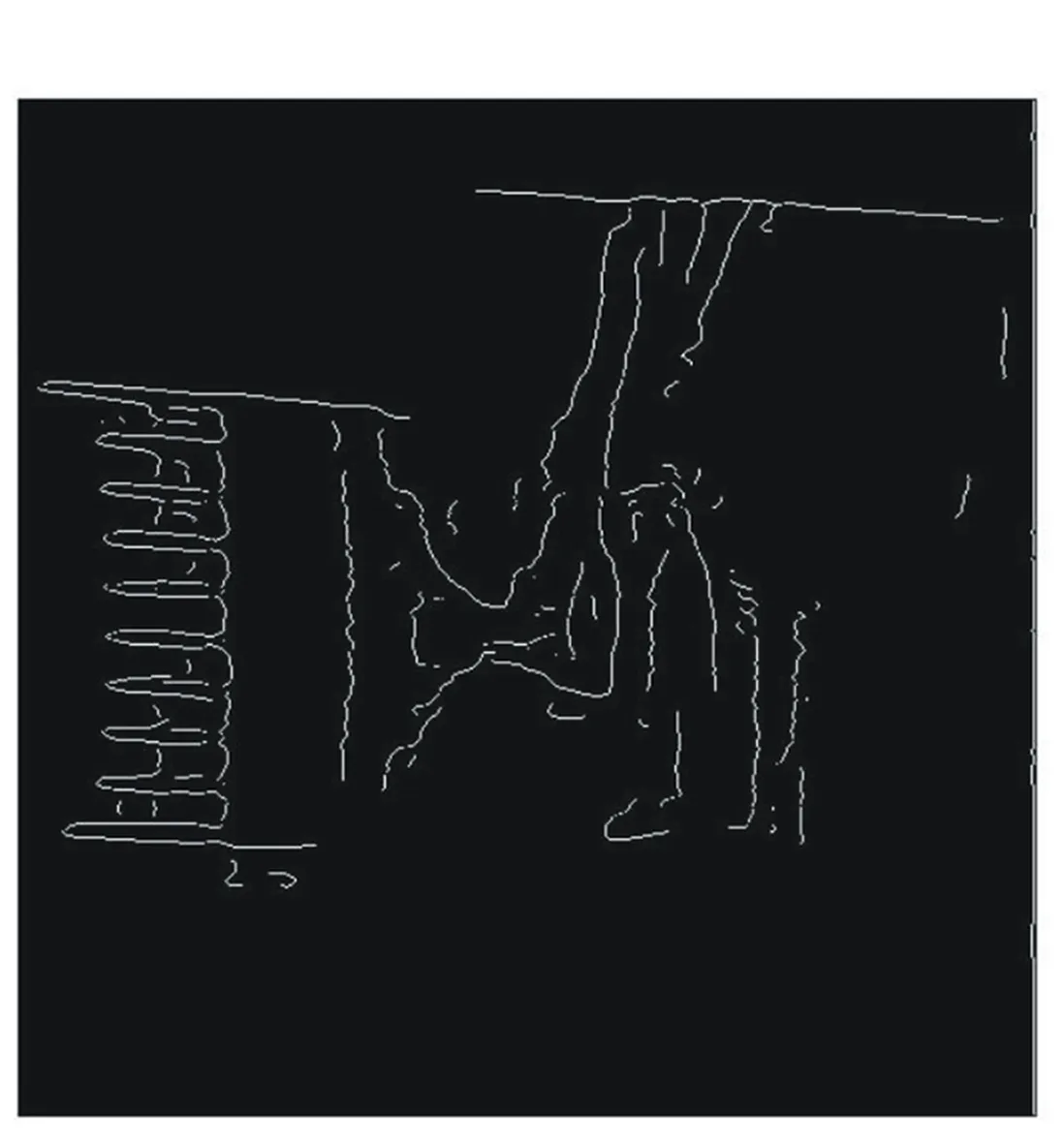
(c)Scale fusion results

图6 核函数拉伸后不同尺度及尺度间数据融合的小波算法边缘检测结果的比较
Fig.6Comparison of edge detection results from wavelet edge detection algorithm

4 结论

针对条纹相机图像的特点，将小波边缘检测算法的核函数在特定方向进行伸缩，使算法对条纹相机图像的纵向条纹不敏感，抑制了伪边缘的产生，同时保持了较高的空间分辨率；利用Paul提出的数据融合算法，将不同尺度下小波边缘检测算法的结果进行融合，融合后算法保留了大尺度下不易产生伪边缘和小尺度下边缘定位更精细的优点。

[1] 盛亮, 王亮平, 李阳, 等. 平面丝阵负载Z 箍缩内爆动力学一维图像诊断[J].物理学报, 2011，60(10): 105205(SHENG Liang, WANG Liang-ping, LI Yang, et al. One-dimensional

imaging diagnostics of imploding dynamics for planar wire array Z pinch[J]. Acta Phys Sin, 2011, 60(10): 105205.)

[2]李阳, 盛亮, 张美, 等. 小波边缘检测算法在平面丝阵Z箍缩图像1维诊断中的应用[J].强激光与粒子束, 2011, 23(10): 2 786-2 790.(LI Yang, SHENG Liang, ZHANG Mei, et al. Wavelet edge detection in one-dimensional imaging diagnostics for planar wire array Z-pinch[J]. High Power Laser and Particle Beams, 23(10): 2 786-2 790.)

[3]MARR D, HILDRETH E C. Theory of edge detection[J]. Proc R Soc Lond B Biol Sci, 1980, 207(1 167): 187-217.

[4]CANNY J F. A computational approach to edge detection[J]. IEEE Trans Pattern Anal Mach Intell, 1986, 8(6): 679-698.

[5]CANNY J F. Finding edges and lines in images[R]. Technical Report AI-TR-720, Artificial Intelligence Laboratory, Cambridge, MA, 1983.

[6]马特拉. 信号处理的小波导引[M]. 2版. 北京: 机械工业出版社, 2003: 142-138.(MALLAT I S. A Wavelet Tour of Signal Processing[M]. 2nd ed. Beijing: China Machine Press, 2003: 142-148.)

[7]CHEN W F, LU X Q, CHEN J J, et al. A new algorithm of edge detection for color image: Generalized fuzzy operator[J]. Science in China Ser A, 1995, 38(10): 1 272-1 280.

[8]胡守仁. 神经网络应用技术[M]. 长沙：国防科技大学出版社，1993.(HU Shou-ren. Applied Technologies of Neural Network[M]. Changsha: National University Defense Industry Press, 1993.)

[9] 姜三平. 基于小波变换的图像降噪[M]. 北京: 国防工业出版社, 2009.(JIANG San-ping. Denoising Technologies Based on Wavelet Transform[M]. Beijing: National Defense Industry Press, 2009.)

[10] BAO P, ZHANG L, WU X L. Canny edge detection enhancement by scale multiplication[J]. IEEE Trans Pattern Anal Mach Intell, 2005, 27(9): 1 485-1 490.

[11] PRATT W K. Digital Image Processing[M]. 2nd ed. John Wiley & Sons, 1991.

A Multi-Scale Wavelet Edge Detection Algorithm for Streak Camera Images

LI Yang1,2,3,PENG Bo-dong2,3,SHENG Liang2,3,HEI Dong-wei2,3, LI Kui-nian2,3,ZHANG Mei1,2,3,ZHAO Ji-zhen2,3

(1.Electronic Engineering Department,Xi’an Jiaotong University,Xi’an710049,China;2.Northwest Institute of Nuclear Technology,Xi’an710024,China;3.State Key Laboratory of Intense Pulsed Radiation Simulation and Effect,Xi’an710024,China)

A multi-scale wavelet edge detection algorithm used for streak camera images was presented in this paper. By stretching the kernel function of the wavelet edge detection method in a given direction, we constructed a direction sensitive edge detector, which can suppress the pseudo-edges caused by the electromagnetic interference on streak cameras. Information fusion skills were used to ensure the algorithm with the advantages of the wavelet edge detection method under both larger and smaller scales. Numerical experiments demonstrate that the algorithm proposed in this paper provides accurate edges with less pseudo ones, and it is resistant to the noise.

streak cameras;image processing;edge detection;wavelet edge detection method;multi-scale

2016-06-20；

2016-09-06

强脉冲辐射环境模拟与效应国家重点实验室基金资助项目(SKLIPR1304Z)

李阳(1984- )，男，山东青岛人，助理研究员，博士研究生，主要从事脉冲等离子体研究。

E-mail:liyang@nint.ac.cn

TB 853；O571

A

2095-6223(2016)041201(7)