基于落锤实验平台的爆炸载荷模拟装置原理性设计

程 帅,陈 博,刘文祥,张德志

(西北核技术研究所,西安710024)

基于落锤实验平台的爆炸载荷模拟装置原理性设计

程 帅,陈 博,刘文祥,张德志

(西北核技术研究所,西安710024)

为避免火工品操作带来的危险，可通过载荷发生器产生效应相似的脉冲载荷替代爆炸载荷进行实验。基于落锤实验平台，提出了一种通过液压原理产生半正弦波载荷的方法，建立了系统响应的运动方程和求解载荷压力峰值、持续时间的计算方法，指出通过减小落锤、活塞质量，减小液压缸长度，增大液压缸截面积，增大落锤初始速度等方法可以获得持续时间较短、脉冲峰值较高的半正弦波载荷。通过数值模拟对半正弦波载荷和爆炸载荷效应的相似性进行了验证。

爆炸力学；载荷发生器；半正弦波；落锤试验

端盖法兰是爆炸容器上的常见密封结构。研究爆炸载荷作用下法兰结构的动态响应规律，对爆炸效应防护、爆炸容器设计具有重要意义。目前，针对脉冲载荷作用下法兰结构的动态响应规律的研究相对成熟，Duffey 等将预紧螺栓-法兰结构简化为“双弹簧-质点”模型，推导了脉冲载荷作用下系统的运动控制方程[1]，并基于上述运动方程为1台方形容器设计计算了平板端盖法兰的螺栓预紧力[2]。程帅等进一步简化了Duffey 的分析模型，给出了脉冲载荷作用下预紧螺栓轴向运动的解析解，并通过数值计算进行了验证[3]。上述研究成果均停留在理论推导、数值计算阶段，尚未通过实验验证。

若以爆炸容器作为实验平台开展法兰结构动态响应规律研究，成本过高，且存在一定的危险性。因此，采用常用的冲击动力学实验平台，通过非爆炸方式开展法兰结构动态响应研究，这是一种经济且安全的实验方法。美国MTS公司和加利福尼亚大学实验室基于落锤实验平台，对桥梁结构在爆炸冲击波载荷作用下的结构响应进行了实验研究，获得了重复性较好的实验室数据[4]。曹永智等利用液压伺服试验机及自制的落锤实验设备，研究了在爆炸冲击波或强冲击载荷下，高强混凝土的断裂能随速率的变化规律[5]。李砚召等通过落锤冲击实验的方法，考核了部分预应力混凝土材料的抗爆炸冲击性能[6]。上述研究工作均以落锤实验平台展开，但均未在载荷等效性方面做出讨论。

本文以落锤实验平台为基础，提出了一种半正弦波窄脉冲载荷发生装置的设计思路，通过理论分析和数值模拟，对装置的工作原理进行了分析，推导了脉冲载荷压力峰值、持续时间与结构尺寸间的函数关系；并进一步建立了螺栓-法兰结构的有限元模型，验证了装置产生的半正弦波载荷与爆炸冲击波载荷的等效性，可用于法兰结构动态响应规律的实验研究。

1 脉冲载荷发生装置的工作原理

图 1为设计的脉冲载荷发生装置的工作原理示意图。该装置通过低速落锤撞击活塞压缩液压介质产生半正弦波载荷，如果忽略液压介质的质量和阻尼，可以将装置简化为如图 2所示的弹簧-质量块模型。其中，mh为落锤质量，mp为活塞质量。弹簧的刚度与液压介质的性质及液压缸的几何结构相关。

图1 脉冲载荷发生装置的工作原理图Fig.1Schematic diagram of the pulse loading generator

图2 脉冲载荷发生装置工作原理简化模型Fig.2Simplified model of the pulse loading generator

对于落锤实验平台，当落锤质量远大于液压缸活塞质量时，落锤以一定初速度下落撞击活塞后，二者将以相同的速度继续运动并压缩液压缸。如果将落锤的初始速度记为v0，根据动量守恒定律，落锤与活塞共同下落的速度，可通过式(1)计算：

(1)

其中，v1为落锤与活塞碰撞后落锤的速度；v2为落锤与活塞碰撞后活塞的速度。将活塞的压缩长度记为x(t)，液压介质对活塞产生的压强记为p(x)，活塞截面积记为S，则活塞压缩过程中系统的运动方程为

(2)

如果选用水作为液压介质，在压缩状态下其冲击绝热曲线为

(3)

其中，A1,A2,A3为常数，GPa;B1,B0为无量纲常数[7]。μ为水的压缩率，μ≥0, 可通过式(4)计算出：

(4)

其中，ρ0为初始密度，kg· m-3。在落锤的低速撞击下，液压介质的压缩率较小，μ≈0。根据表 1中给出的状态方程参数[8]，可以得到压缩率较小时水的冲击绝热曲线，如图 3所示。由图3可见，在压缩率较小时，水的冲击绝热曲线可以近似为直线，根据图中数据，拟合其函数为

pH=kμ

(5)

其中，k为比例常数，k=2.7 GPa。综上可以得出：液压缸中的液体压力与压缩率近似为线性关系，即可将图 2简化模型中弹簧的弹性系数视为常数。

表1水在压缩状态下的多项式状态方程参数Tab.1Parameters of polynomial EOS for water under compression

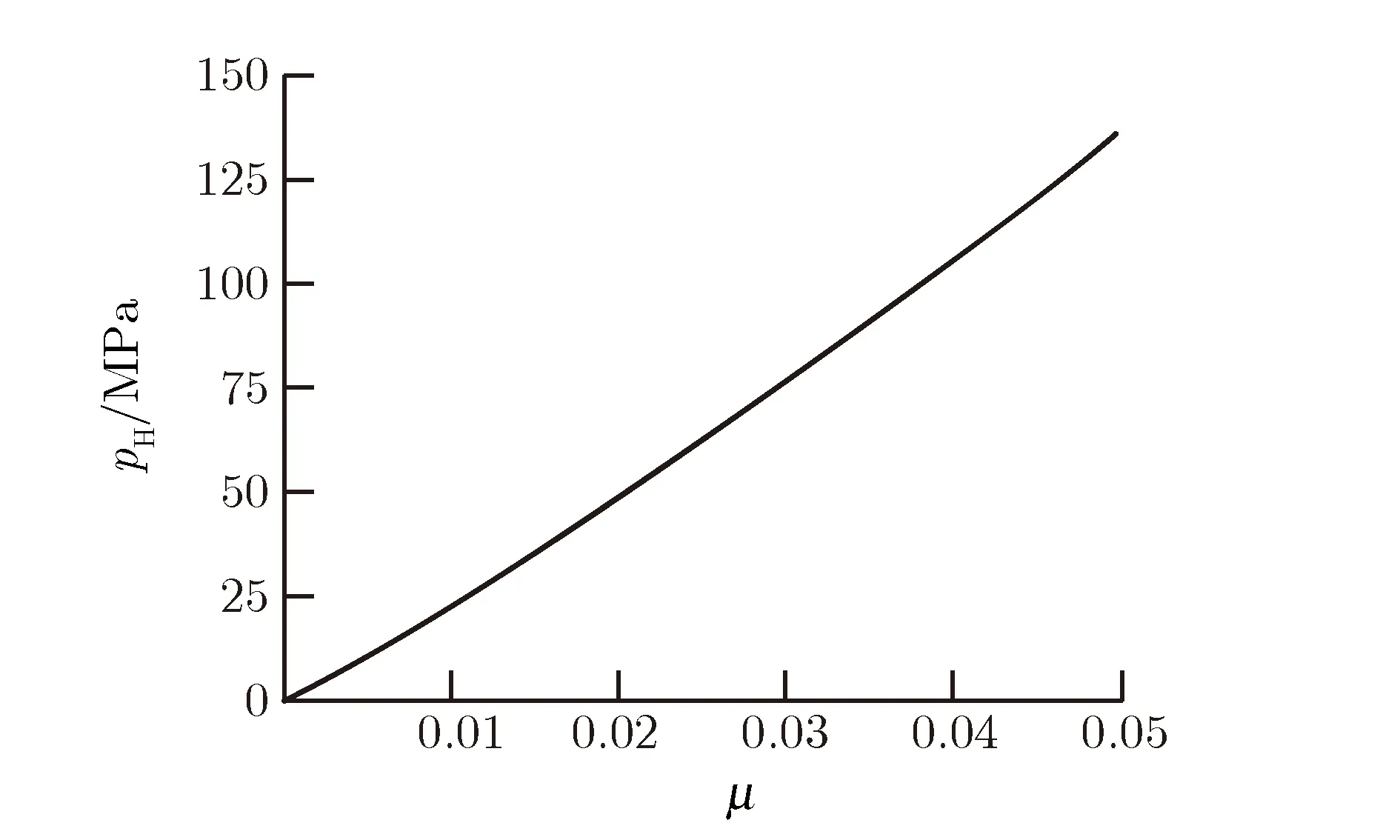
图3 水的冲击绝热曲线Fig.3Hugoniot curve of water

将图 2中活塞沿纵向运动的位移记为x，弹簧的初始长度，即液压缸的长度记为x0，则弹簧的压缩率μ可记为μ=x/x0，因此式(2)可简化为

将活塞初始位移为0和活塞速度v2作为边界条件代入式(6)进行求解，可得到脉冲载荷压力峰值和持续时间的表达式为

(7)

其中，pmax为液压缸产生的脉冲载荷压力峰值，T为半正弦波的持续时间。

由式(7)可知，为了缩短脉冲载荷持续时间，可采取减小落锤和活塞的质量、减小液压缸长度、增大液压缸截面积等方法。如果采用减小液压缸长度或增大液压缸截面积的方法，可以通过式(7)直接计算脉冲载荷持续时间的变化；但若减小落锤质量过多，则落锤与活塞碰撞后不再以共同速度运动，而是彼此”交换速度“，导致物理过程的变化。采用减小液压缸长度和增大液压缸截面积的方法，计算脉冲载荷的持续时间，这个过程比较简单；但减小落锤质量则会导致落锤与活塞碰撞后，二者不再以共同的速度运动，而是彼此“交换速度”。这一过程可以用动量守恒和能量守恒方程描述：

(8)

由式(8)可见，当落锤质量与活塞质量较为接近时，碰撞后落锤速度减小至0；当落锤质量小于活塞质量时，碰撞后落锤将以一定初速度竖直上抛。因此，当落锤质量接近或小于活塞质量时，碰撞后落锤不再对液压介质的压缩过程产生明显的影响，将式(8)代入式(6)，可以得到此时脉冲载荷峰值和持续时间为

(9)

根据式(9)，在活塞质量不变的条件下，减小落锤质量可以显著降低半正弦波载荷的持续时间，但随着落锤质量的逐渐减小，活塞压缩介质产生的载荷压力峰值也随之下降，因此落锤质量也不宜过小。考虑到完全弹性碰撞情况下，当落锤质量与活塞质量相等时，落锤下降的动能将全部转化为活塞的动能压缩介质，系统的能量转化率达到最高，因此设计中尽量使落锤质量与活塞质量保持一致。

2 数值模拟验证

为验证半正弦波窄脉冲载荷发生器的工作原理，对分析结果进行了数值模拟。图 4为通过商业软件建立的数值计算模型示意图。图中落锤、活塞采用普通碳钢材料；液压介质为水。除与活塞接触面之外,将液压介质的其他边界设定为刚性壁面，并对液压介质右侧边界中点处的压力载荷进行了分析。

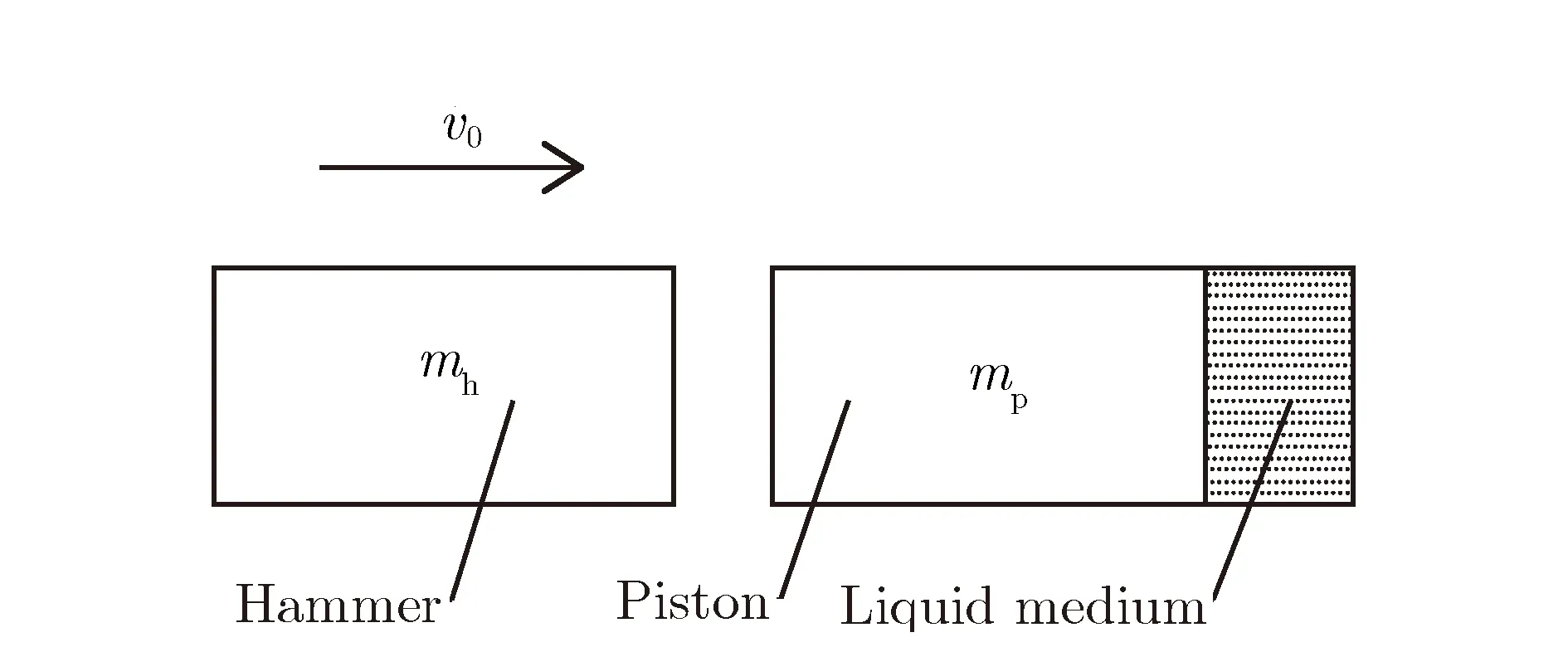
图4 数值计算模型Fig.4Numerical simulation model

数值计算模型采用的基本参数如表 2所列。其中，工况1-工况5中落锤质量远大于活塞质量，工况6-工况10中落锤质量接近或小于活塞质量。采用控制变量法，对比分析落锤质量、落锤初速度、液压缸长度和液压缸截面积对脉冲载荷特性的影响与理论分析结果是否符合。

表2 数值计算模型参数设置Fig.2Parameters of numerical simulation models

图5给出了工况1-工况5的数值模拟脉冲载荷波形，表3对比了各工况发生的脉冲载荷压力峰值、持续时间的解析结果和数值模拟结果。由计算结果可知：利用式(7)计算出的脉冲载荷压力峰值和持续时间与数值模拟结果基本一致；同时，当落锤质量、落锤初速度、液压缸长度和液压缸截面积发生变化时，与之相应的脉冲载荷压力峰值和持续时间的变化倍数也同式(7)的计算结果一致。由此证明了当落锤质量远大于活塞质量时，理论分析结果的可靠性。

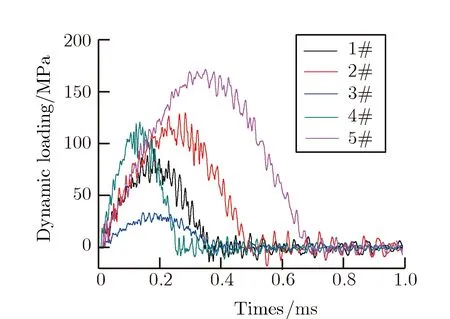
图5 脉冲载荷时间历程模拟计算结果(1#--5#)Fig.5Numerical simulation of dynamic loading time history (1#--5#)

No.pmax/MPaAnalyticalNumericalT/msAnalyticalNumerical175800.370.3621081140.510.51330300.370.3641071110.260.2551511650.740.69

图6给出了工况6-工况10的数值模拟载荷波形，表4对比了各工况的脉冲载荷压力峰值、持续时间的解析求解和数值模拟结果。由计算结果可以看到，由式(9)计算出的载荷压力峰值和持续时间与数值模拟结果基本一致；同时当落锤质量、落锤初速度、液压缸长度和液压缸截面积发生变化时，载荷压力峰值和载荷持续时间的变化的倍数也同式(9)的计算结果具有较好的一致性。由此证明了当落锤质量与活塞质量接近时，理论分析结果的可靠性。

对上述的理论推导结果进行了数值模拟，并论证了以落锤实验机为平台，通过减小液压缸长度、增大液压缸截面积等方法，产生半正弦波窄脉冲载荷的可行性。

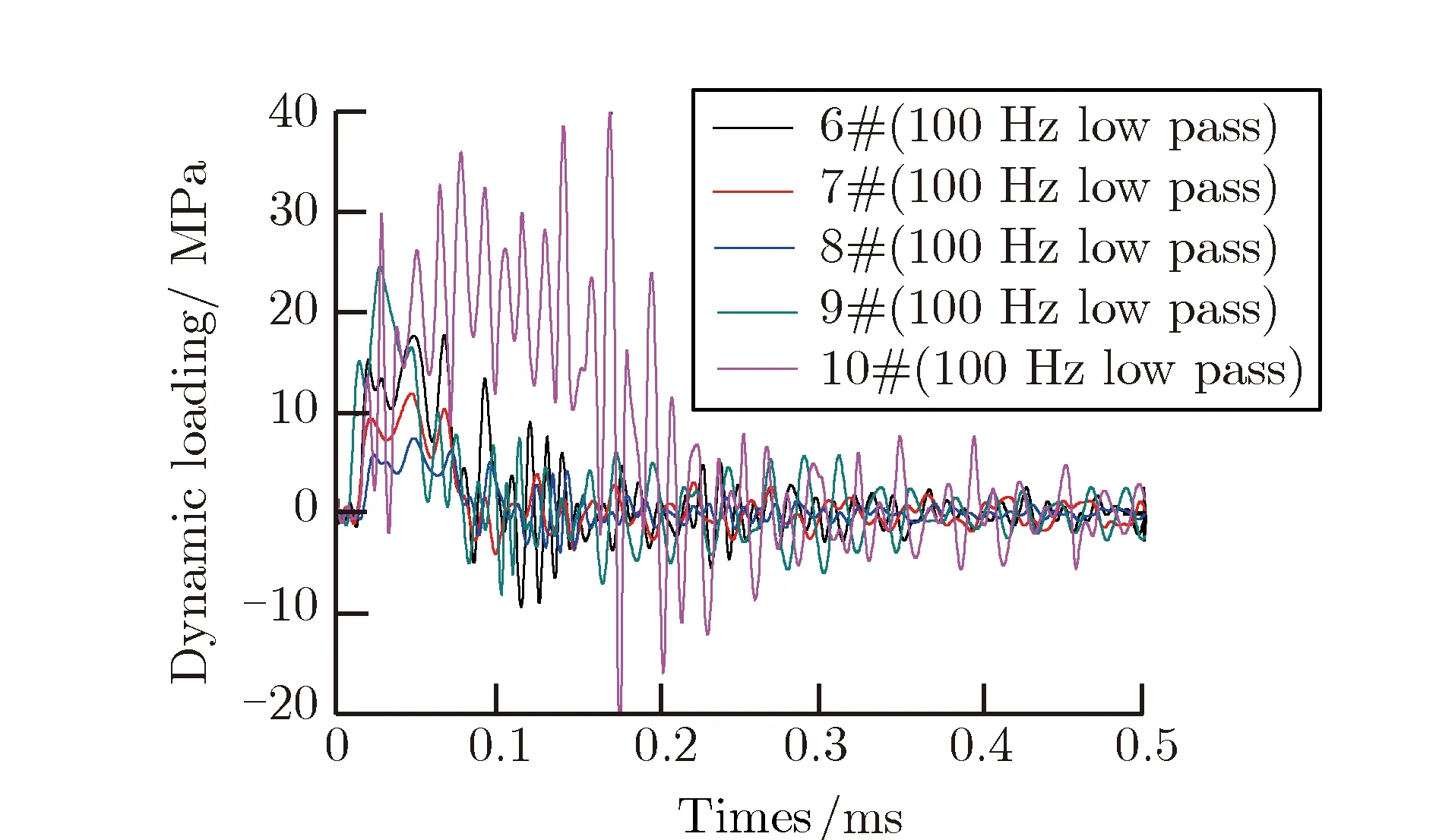
图6 脉冲载荷时间历程模拟计算结果(6#--10#)Fig.6Numerical simulation of dynamic loading time history(6#--10#)

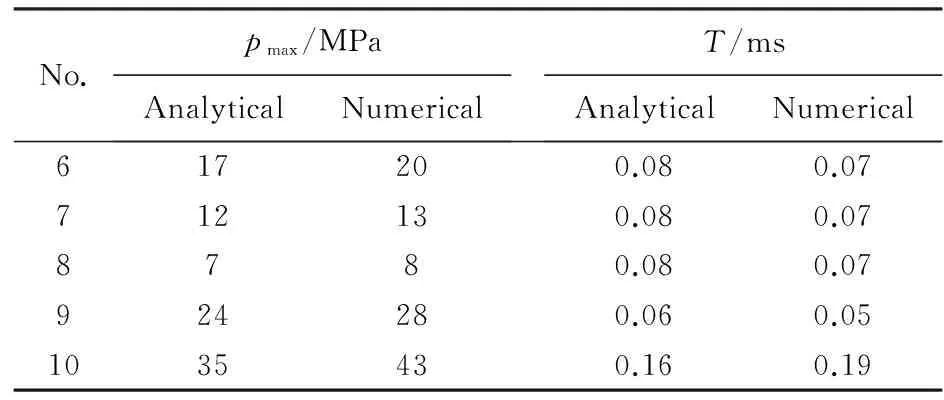
No.pmax/MPaAnalyticalNumericalT/msAnalyticalNumerical617200.080.07712130.080.078780.080.07924280.060.051035430.160.19

3 半正弦波与爆炸冲击波载荷的等效性

本文设计的半正弦波脉冲发生装置主要用于产生替代冲击波的载荷，用以研究法兰结构的动态响应及密封性能。图7给出了法兰的基本结构，包括法兰端盖、法兰接管以及高强螺栓。其中，法兰内直径为125 mm、外直径为200 mm、法兰和端盖的厚度均为20 mm, 二者通过12根M12的高强螺栓连接。装配时对螺栓预紧，使其压紧密封面，工作时爆炸冲击波作用于端盖内表面，在动态响应过程中，可根据端盖和法兰密封面的间隙，观察系统的密封情况。

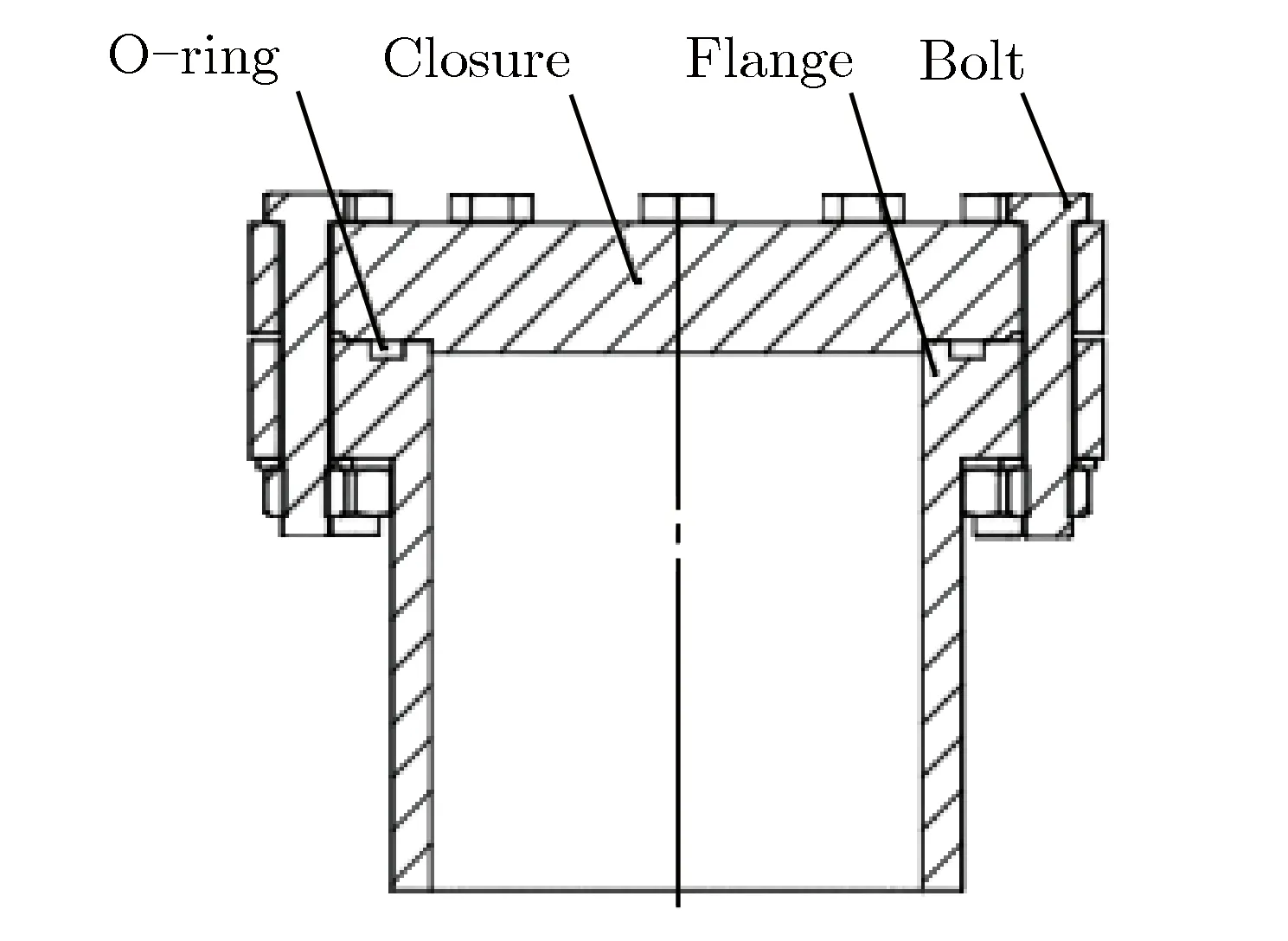
图7 法兰的基本结构Fig.7Structure of the flange

根据图 7中法兰的结构尺寸建立了数值计算模型，如图 8所示。该模型为1/12中心对称的结构。在法兰底部添加了约束轴向位移的边界条件。法兰、端盖和螺栓的材料模型全部选取弹性模型，弹性模量为200 GPa；螺栓有效工作截面的直径为10 mm，计算前，向螺栓施加100 MPa的轴向预紧力。由模态分析结果可知，系统的自振周期约为200 μs。

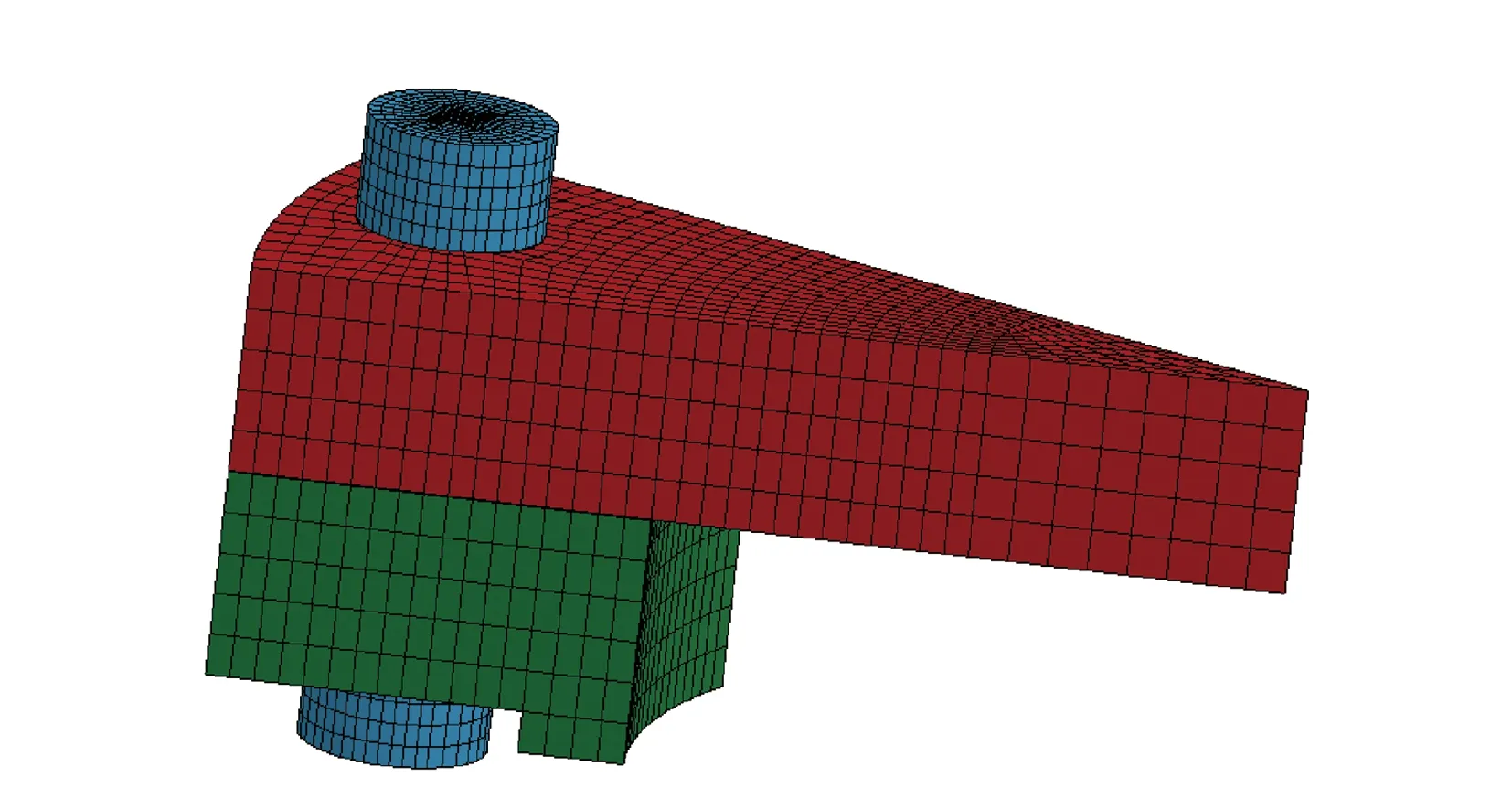
图8 等效性数值模拟模型Fig.8Simulation model for equivalence discussion

利用上述分析模型对半正弦波脉冲与冲击波载荷的等效性进行了研究。首先讨论了脉冲载荷持续时间大于系统响应周期的2倍工况，以下的分析中将此类载荷简称为长脉冲载荷。如图 9所示，在端盖内侧施加三角波冲击载荷和正弦波脉冲，其中，三角波载荷压力峰值20 MPa，持续时间400 μs，约为系统自振周期的2倍。用于等效性分析的2条正弦波载荷的持续时间与三角波保持一致，其中，正弦载荷曲线1的压力峰值与三角波一致，正弦波载荷曲线2的冲量与三角波一致。由图10的系统动态响应曲线可以看到，在长脉冲载荷工况下，正弦波载荷曲线1作用下的法兰间隙压力峰值与三角波作用下的基本一致。说明，在长脉冲载荷条件下，采用压力峰值等效的方法能够获得相似的动态响应结果，也说明载荷持续时间较长时，载荷压力峰值是影响动态响应的主要因素。

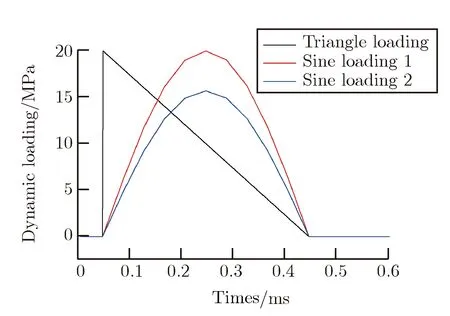
图9 长脉冲载荷Fig.9Long-decay pulse loading

图10 长脉冲载荷下结构响应Fig.10Dynamic response to long-decay pulse

与长脉冲载荷相对应的为窄脉冲载荷，如图 11所示。图11中,三角波脉冲的压力峰值为60 MPa，持续时间为100 μs，约为系统振动周期的1/2。为研究半正弦波脉冲与三角波脉冲的等效性，共计算了4条正弦波载荷作用下系统的动态响应，其中，曲线1--曲线3的载荷冲量与三角波相等，载荷1的持续时间与三角波保持一致，载荷2和载荷3的持续时间分别为三角波载荷的1/2和2倍；载荷4的峰值和持续时间同三角波脉冲保持一致。

图12给出了上述载荷曲线作用下系统动态响应的法兰间隙变化。由图12可见，当半正弦波载荷的冲量和持续时间与三角波载荷相一致时，系统动态响应的法兰间隙变化曲线的一致性较好，这表明采用冲量、时间等效的方法可以获得相似的动态响应结果，也说明窄脉冲载荷条件下，系统的动态响应主要受载荷冲量和持续时间的影响。

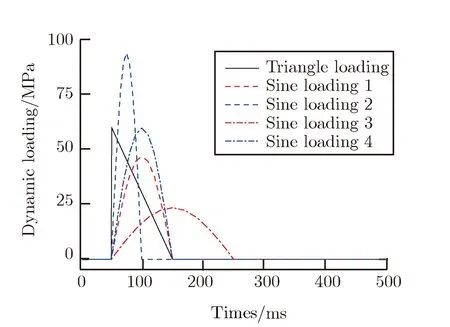
图11 窄脉冲载荷Fig.11Short-decay pulse loading

图12 窄脉冲载荷下结构响应Fig.12Dynamic response to short-decay pulse

4 结论

基于落锤实验平台，设计了一种能够产生半正弦波脉冲载荷的装置，可替代爆炸冲击载荷开展法兰动态响应的研究实验。采用减小落锤和活塞质量、减小液压缸长度和增大液压缸截面积等方法，获得了持续时间较短的半正弦波脉冲，通过提高落锤的初速度，可以提高产生载荷的压力峰值。脉冲载荷装置产生的半正弦波载荷与爆炸冲击波载荷具有相似的作用效果。载荷持续时间大于系统振动周期2倍时，压力峰值和持续时间相同的半正弦波载荷与爆炸冲击载荷作用效果相似；载荷持续时间小于系统振动周期的1/2时，冲量和持续时间相同的半正弦波载荷与爆炸冲击载荷的作用效果相似。

[1]DUFFEY T A. Optimal bolt preload for dynamic loading[J]. Int J Mech Sci, 1993, 3(35): 257-265.

[2]DUFFEY T A, LEWIS B B, BOWERS S M. Bolt preload selection for pulse-loaded vessel closures[C]// ASME/JSME Pressure Vessels and Piping Conference, Honolulu, 1995: 167-174.

[3]程帅, 刘文祥, 张德志, 等. 脉冲载荷作用下预紧螺栓-法兰结构的动态响应[C]//第十一届全国爆炸力学学术会议, 珠海: 2016. (CHENG Shuai, LIU Wen-xiang, ZHANG De-zhi, et al. Dynamic response of preloaded bolt-flange structure under impulsive loading[C]//The 11th National Conference on Explosive Mechanics, Zhuhai: 2016.)

[4]GRAM M M, CLARK A J, HEGEMIER G A, et al. Laboratory simulation of blast loading on building and bridge structures[C]// Structures under Shock and Impact, 2006.

[5]曹永智, 张生坦, 孟庆鑫. 高强混凝土断裂能加载速率效应研究[J]. 建筑材料学报, 2010, 13(1): 90-94. (CAO Yong-zhi, ZHANG Sheng-tan, MENG Qing-xin. Effect of loading rate on fracture energy of high-strength concrete[J]. Journal of Building Materials, 2010,13(1): 90-93.)

[6]李砚召, 王肖军, 郭晓辉, 等. 部分预应力混凝土梁抗冲击性能试验研究[J]. 爆炸与冲击, 2006, 26(3): 256-261. (LI Yan-zhao, WANG Xiao-jun, GUO Xiao-hui, et al. Experimental study on anti-impact properties of a partially pre-stressed concrete beam[J]. Explosion and Shock Waves, 2006, 26(3): 256-261. )

[7]李晓杰, 张程娇, 王小红. 水的状态方程对水下爆炸影响的研究[J]. 工程力学, 2014, 31 (8): 46-52. (LI Xiao-jie, ZHANG Cheng-jiao, WANG Xiao-hong, et al. Numerical study on the effect of equation of state of water on underwater explosion[J]. Engineering Mechanics, 2014, 31(8): 46-52.)

[8]李晓杰, 张程娇, 闫鸿浩. 水下爆炸近场非均熵流的特征线差分解法[J]. 爆炸与冲击, 2012, 32(6): 604-608. (LI Xiao-jie, ZHANG Cheng-jiao, YAN Hong-hao, et al. Difference method of characteristics in isentropic flow on underwater explosion in near-field region[J]. Explosion and Shock Waves, 2012, 32(6): 604-608.)

(上接第040602-5页)

[4] 李庆民, 吴明雷, 张国强. 铁磁性材料在抑制GIS高频暂态应用中的仿真分析方法[J]. 电工技术学报, 2005, 20(11): 30-34.(LI Qing-min, WU Ming-lei, ZHANG Guo-qiang. Simulating and analyzing method for the applications of ferromagnetic materials in suppressing high frequency transients within GIS [J]. Transactions of China Electromagnetical Society, 2005, 20(11): 30-34 )

[5]项祖涛, 刘卫东, 钱家骊, 等. 用磁环抑制GIS的VFTO的高电压模拟试验[J]. 电工技术学报, 2004, 19(7): 1-3. (XIANG Zu-tao, LIU Wei-dong, QIAN Jia-li, et al. High voltage simulation tests of suppressing VFTO in GIS by magnetic rings[J]. Transactions of China Electromagnetical Society, 2004, 19(7): 1-3.)

[6] IEC61000-2-10. Environment description of HEMP environment-conducted disturbance[S]. 1998.

[7] 朱长青, 刘尚合, 魏明. 强电磁脉冲的有效带宽、测量带宽及来自上升时间的影响[J]. 强激光与粒子束, 2005, 17(1): 99-103. (ZHU Chang-qing, LIU Shang-he, WEI Ming.High-EMP effective bandwidth, measurement bandwidth and effect from rising time[J]. High Power Laser and Particle Beams, 2005, 17(1): 99-103.)

[8] SHI L H, TAN J W, ZHOU B H. Time domain calibration of pulsed current probe[C]//17th International Zurich Symposium on Electromagnetic Compatibility, 2006: 296-299.

[9] 严密， 彭晓领. 磁学基础与磁性材料[M]. 杭州：浙江大学出版社, 2004. (YAN Mi, PENG Xiao-ling. Fundamentals of Magnetic and Magnetic Materials[M]. Hangzhou: Zhejiang University Press, 2004.)

[10] 何金良. 电磁兼容概论[M]. 北京：科学出版社， 2010. (HE Jin-liang. Electromagnetic Compatibility[M]. Beijing: Science Press, 2010.)

Theoretical Design of an Explosive Loading Analogue Device Based on Drop Hammer Test System

CHENG Shuai,CHEN Bo,LIU Wen-xiang,ZHANG De-zhi

(Northwest Institute of Nuclear Technology,Xi’an710024,China)

Using impulse loading produced by a generator, which has similar effect with an explosive loading in experimental research, is a good way to overcome the shortcomings of high risk of explosive operation. In this paper, an impulsive loading generator is devised based on a drop hammer test system, which will produce a half sine loading by compressing liquid medium in an oil cylinder. The controlling equation of the dynamic response process is performed and the analytical solution is obtained which suggests that a half sine loading with higher peak and shorter decay will be generated by decreasing the masses of drop hammer and piston, decreasing the length of the oil cylinder, increasing the section areas of the oil cylinder or increasing the initial velocity of the hammer. Discussion on the equivalence between the half sine loading and explosive loading is also carried out, showing that they share the similar effect.

explosive mechanics;loading generator device;half sine loading;drop hammer test

2016-04-25；

2016-11-10

程帅(1988- ), 男, 黑龙江哈尔滨人, 助理工程师, 硕士, 主要从事冲击动力学研究。

E-mail:chengshui@nint.ac.cn

TL812

A

2095-6223(2016)041002(7)