基于平面棋盘格标定板的三维空间标定新方法

王向东， 董琦奇

(国家体育总局体育科学研究所，北京 100061)

基于平面棋盘格标定板的三维空间标定新方法

王向东， 董琦奇

(国家体育总局体育科学研究所，北京 100061)

在总结分析国内外摄像机标定技术研究的基础上，针对体育科研中使用三维立体框架进行摄像机标定在标定范围、误差、便携性及时效性等方面存在的不足，提出了使用平面棋盘格标定板进行三维空间标定的新方法。选取了5 m、10 m和30 m的拍摄距离，标定参照物选用传统三维辐射式立体框架和自制二维平面棋盘格标定板，对标准1 m长度的比例尺进行三维重建，对两种标定方法进行了精度比较。此外还对标准1 m板在测量空间的不同位置（测量画面中间、边缘）进行了误差分布分析。实验结果表明，基于平面棋盘格标定板的摄像机空间标定方法具有一定的优势，不论从使用方便性还是测量精度方面都克服了三维立体框架在使用中的不足，理论上能够满足体育科研的需求。

体育科研；运动生物力学；三维立体框架；摄像机标定；平面标定

录像解析是体育科研中常用的研究手段，通过对运动技术图像的解析可以在不影响正常比赛和训练的前提下，较真实地获得运动员比赛时的运动学参数，对摄像机进行准确的三维空间标定是录像解析的前提。目前国内外的运动生物力学研究领域中，依然是使用三维立体框架对摄像机进行标定，这种方法存在着一定的不足和局限：①对实际测量的标定范围有限，无法对大范围运动项目进行有效的标定，甚至有时因比赛现场拍摄位置的特殊性而导致无法测量；②随着使用时间的增长，框架会因自身形变等原因而导致测量误差的增大；③这种框架相对比较笨重，携带不方便，在体育比赛现场安装费时费力；④在标定时还需要人工对框架的标记点进行识别，大大增加标定的时间[1-4]。以上问题对体育科学研究造成了一定的影响，因此需要一种新的方法替代传统的三维立体框架标定，以达到在标定时方便、快捷、有效的目的。

随着计算机图像技术在三维人体模型重建、运动目标检测等方面的应用，摄像机标定也成为了近年来计算机视觉领域广泛关注的一个研究热点[5-13]。在计算机视觉领域中，通过平面棋盘格对摄像机进行空间标定理论上比较成熟。因此，本研究将使用平面棋盘格标定板替代原有体育科研中常用的三维立体框架来对所使用的摄像机进行标定，通过统计学的方法对两种标定方法的标定结果进行精度验证和误差分析，检验基于平面棋盘格标定板的标定方法能否满足体育科研大范围、高精度的实际需求。

1 研究方法

1.1 平面标定原理

摄像机标定用于求摄像机的内参和外参，本文采用的是张正友摄像机标定方法[14-15]。

在计算机视觉中，平面的单应性被定义为从一个平面到另一个平面的投影映射。因此一个二维平面上的点映射到摄像机成像仪上的映射就是平面单应性的例子。单应性矩阵表示把一个平面点映射到另一个平面上，从物体平面到图像平面的映射，同时表征了这两个平面的相对位置和摄像机投影矩阵(图1)。

1.2 双目视觉的三维重建

使用双摄像机成一定角度对同一场景进行拍摄得到两幅数字图像，如图 2所示。假设摄像机的内外参数是已知，即投影矩阵M的值确定，且空间任意点 P在两幅图像中的位置也已经被检测出来。由解析几何的知识可知，三维空间的平面方程是线性方程，两个平面方程联立所得的解为空间中的一条直线(两平面交线)，解得两射线的交点即得P的空间三维坐标(X, Y, Z)。

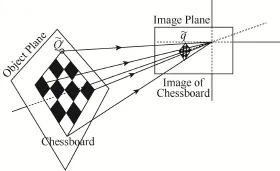
图1 单应性来描述平面物体的观测

图2 双目视觉的三维重建

1.3 研究内容

本文实验拍摄距离选取了5 m、10 m和30 m，拍摄空间范围为4 m(长)×4 m(宽)×3 m(高)，使用两台Canon HF M52家用式常速高清摄像机(分辨率为 1920×1080)，标定参照物选用传统三维辐射式立体框架和自制二维平面棋盘格标定板(规格为1 m×1 m，硬度较高，形变较小的标准平面棋盘格标定板，棋盘格图案边长为91 mm，9×9个角点)，对标准1 m长度的比例尺进行三维重建。实验对使用三维辐射式立体框架拍摄后的画面，通过Simi Motion三维运动解析系统进行解析。对使用二维平面棋盘格标定板拍摄后的画面通过自编解析系统进行计算。然后对传统直接线性变换算法(direct linear transformation，DLT)和基于OpenCV标定的重建结果精度进行比较。

1.4 数理统计法

本文实验所得数据通过 Microsoft Excel对数据进行归一处理分析，并使用SPSS Version 20统计分析软件，对数据进行数理统计、独立样本 T检验、单因素方差分析以及相关性分析，P〈0.05表示具有显著性差异，P〈0.01表示具有非常显著性差异，P〉0.05表示无显著性差异。

2 实验方案

图 3为本研究三维重建的技术路线图，着重对不同标定物从特征点提取到获取摄像机参数的两种技术方法对其重建结果的误差进行分析比较：①用左右两台不同方位的摄像机对标定物拍摄并获取图像；②对左右两台摄像机获取的图像进行处理后，从中对特征点进行提取和匹配，进而获得摄像机的内部参数和外部参数；③利用两种方法的测量原理，通过特征点及摄像机的内外参数，计算得到1 m板的三维重建结果。

图3 三维重建技术路线图

2.1 传统三维立体框架标定

如图 4所示，将摄像机分别摆放距标定空间中心组装好的三维标定框架5 m、10 m及30 m的位置，两摄像机夹角为 60°～120°，通过对摄像机调焦，选取实验所需的最佳拍摄空间，将三维标定框架放置于图像中心进行拍摄，并且在测量空间范围内不同的位置移动标准1 m板进行拍摄。

图4 传统方法标定

将左右两机的框架和1 m板图像以及三维标定框架的原始三维坐标信息导入Simi Motion三维运动解析系统中，对左右两机对应的三维标定框架的25个标定点(图5)和1 m板的4个端点分别进行打点标记处理，通过计算得到并导出最终标准1 m长度板A、B、C、D等4个端点的三维坐标值，通过计算从而可以得到AB、CD之间的三维重建距离，即每幅图像中1 m板的两次长度重建的距离。

图5 导入框架坐标及对25个标定点打点标记处理

2.2 平面棋盘格标定

摄像机摆放位置及摄像机参数设置与传统方法相同，分别对标准1 m板、平面棋盘格标定板进行拍摄(图6)：①分别通过左右两台摄像机单独拍摄若干张置于图像中心的棋盘格标定板不同角度的图像；②通过左右两机同时拍摄若干张棋盘格标定板不同角度的图像和在空间范围内不同位置移动的标准1 m板的图像，对拍摄后的图像进行处理；③通过自编系统自动提取图像特征点并与标定板特征点进行匹配(图7)，系统自动求出左右摄像机内参数与外参数，得到相应的参数文件之后进行双目标定，得出棋盘格标定板每个格子的长度与标准长度的差值以及重建长度的分布数据，利用软件得到左右两台摄像机拍摄画面的标准1 m板4个端点A、B、C、D所对应的二维投影坐标信息后，可由系统重建得到1 m板4个端点 A、B、C、D的三维坐标值，从而通过计算可以得到AB、CD之间的三维重建距离。

图6 棋盘格标定

图7 自动寻找棋盘格角点

3 研究结果与讨论

本文实验在5 m、10 m以及30 m的拍摄距离，通过3种不同的测量标定方法对标准1 m板进行标定重建，对其重建的结果进行精度误差比较。

3.1 两种标定方法重建结果的误差比较

实验测量距离在5 m、10 m及30 m时，对1 m板用三维立体框架及平面棋盘格标定板两种标定物分别拍摄，选取对1 m板标定后的实际测量值与标准值绝对误差进行组间差异分析(表1)。

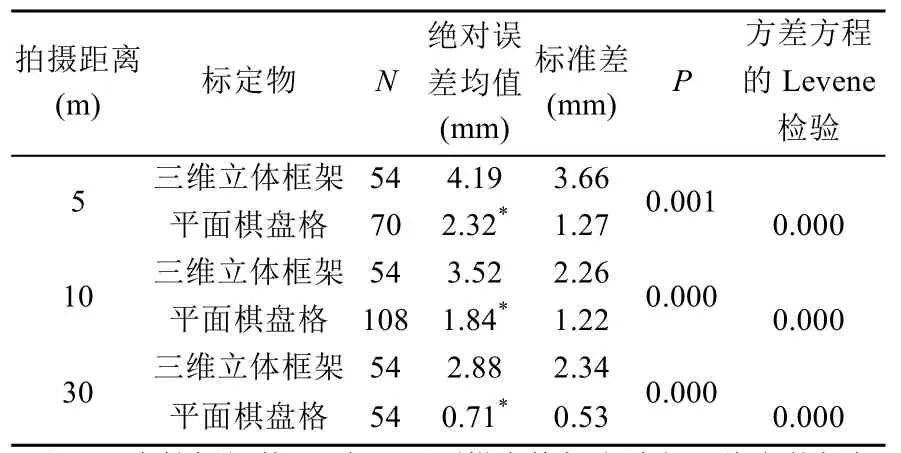
表1 两种标定物3种拍摄距离下测量值与标准值绝对误差的组间差异

使用独立样本 T检验，比较三维立体框架和平面棋盘格两种不同标定物对1 m板测量值与标准值绝对误差的差异。结果表明，平面棋盘格标定相比三维立体框架的测试结果误差更小，检验结果显示具有非常显著性差异(P〈0.01)，即在3种拍摄距离下，使用平面棋盘格标定法比使用传统三维立体框架标定法的精度更高，绝对误差更小。

比较结果显示，使用平面棋盘格标定法的结果分布均匀，更接近于标准值，而传统的三维立体框架标定结果相对不太稳定，可能由于多种因素造成，如摄像机的参数，框架的覆盖范围以及人工标定时产生的偏差等。

3.2 平面棋盘格标定板组间差异比较

对使用平面棋盘格标定板在不同拍摄距离下进行误差趋势分析，进而发现其误差变化规律，如表2所示。

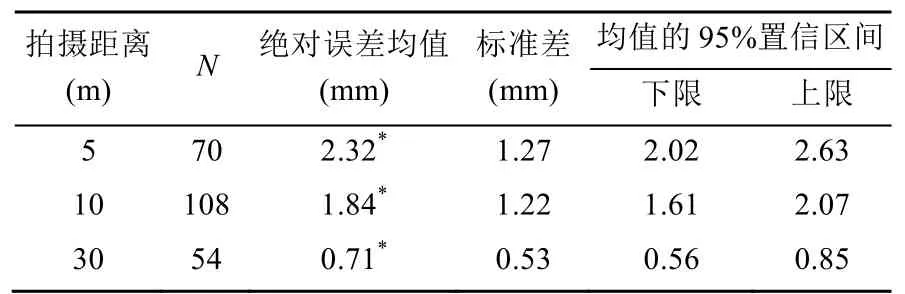
表2 平面棋盘格标定板不同拍摄距离下测量值与标准值绝对误差的组间差异

表 2为使用单因素方差分析平面棋盘格标定板不同拍摄距离下绝对误差的组间差异，结果显示 3种不同拍摄距离下存在非常显著性差异(P〈0.01)。

方差同质性检验显示 3组测量值方差不齐，因此选择Dunnett C进行两两组间比较。结果显示：①5 m、10 m和30 m拍摄距离下测量值与标准值绝对误差两两组间均呈显著性差异；②30 m拍摄距离下的测试结果误差值最小，优于10 m和5 m拍摄距离下的结果。

如图8所示，为使用两种标定物对1 m板重建的结果误差随拍摄距离的增大而减小，其中平面棋盘格标定板的下降趋势更为显著。

图8 两种标定物在不同拍摄距离下对1 m板测试结果的测量值与标准值绝对误差均值图

3.3 1 m板位于标定板控制范围不同位置的误差分布分析

在5 m、10 m和30 m的拍摄距离，分别对1 m板位于标定板控制范围内、控制范围边缘和控制范围外(图9) 3种不同位置的测试结果进行误差分布分析。

通过对3种拍摄距离下所有1 m板位于平面棋盘格标定板不同空间位置下的测试结果进行分析，发现其相对位置之间的误差分布规律，如表3所示。

图9 1 m板与平面棋盘格标定板的3种相对位置关系

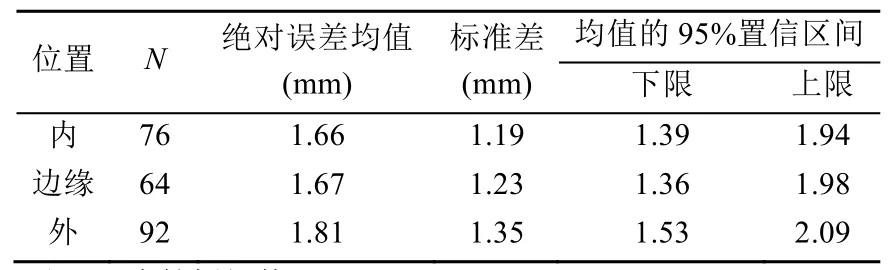
表3 1 m板位于平面棋盘格标定板不同空间位置下测试结果绝对误差的组间差异

使用单因素方差分析对表 3数据进行组间差异分析，结果显示1 m板位于平面棋盘格标定板空间内、边缘及外时P=0.709，无显著性差异，说明使用平面棋盘格标定板对物体标定，不论被标定物是否包含在控制点范围内都具有较高的精度，克服了以往三维立体框架标定的不足。

4 结 论

本文研究工作围绕使用平面棋盘格标定板替代三维立体框架标定物在体育场景中进行摄像机标定，重点在精度方面进行了对比研究，完成了一系列相关的实验，达到了预期结果，主要研究结果如下：

(1) 在同等拍摄条件下，当5～30 m的拍摄距离时，平面棋盘格标定测量得到的结果精度范围在2 mm内，明显优于传统三维立体框架标定结果的2～4 mm，且使用平面棋盘格标定板标定的数据结果更趋于稳定；同时数据显示，测试结果的误差随着拍摄距离的增大而减小，即在拍摄同画面范围的情况下，相机与被测物距离越远重建结果精度越高。

(2) 在拍摄画面中，当被标定1 m板处于平面标定板控制范围内、边缘及外时，空间误差分布数据结果显示1 m板的测量误差都在2 mm以内。

(3) 在标定操作过程中，棋盘格标定法以电脑自动标定标记点代替了以往的人工标定标记点，从而减少了标定过程中影响误差的人为因素，此标定结果显示平面棋盘格标定从理论上可以代替以往三维立体框架标定的使用。

[1] 卢德明. 运动生物力学测量方法[M]. 北京: 北京体育大学出版社, 2001: 33-43.

[2] 郑 义, 曲 峰, 周兴龙. 三维摄像方法中超出标定范围进行标定的精度分析[J]. 首都体育学院学报, 2008, 20(6): 95-97.

[3] 陈 召, 柏开祥, 康 帆. 三维摄影框架的设计、标定、检验与应用研究[J]. 武汉体育学院学报, 2013, 47(1): 65-69.

[4] 贾 谊, 许建辉. 光电子立体摄影测量技术在体育动作分析中的应用[J]. 运动, 2012, (23): 50-52.

[5] 赵 宇. 有标记点的人体三维运动数据获取方法的研究[D]. 哈尔滨: 哈尔滨工业大学, 2008.

[6] 徐 杰. 机器视觉中摄像机标定Tsai两步法的分析与改进[J]. 计算机工程与科学, 2010, 32(4): 45-48,58.

[7] 王建华, 冯 帆, 梁 伟, 等. 非线性模型下的摄像机标定[J]. 光电子技术, 2012, 32(1): 33-38.

[8] 马 伟. 计算机视觉中摄像机定标综述[J]. 价值工程, 2013, (24): 193-194.

[9] 胡占义, 吴福朝. 基于主动视觉摄像机标定方法[J].计算机学报, 2002, 25(11): 1149-1156.

[10] 伍雪冬, 蒋新华, 李建兴, 等. 计算机视觉中传统摄像机定标方法综述[J]. 福建工程学院学报, 2007, 5(1): 57-61.

[11] 刘克明. 中国图学投影理论及其研究[J]. 图学学报, 2014, 35(2): 155-160.

[12] 杨智尧, 宋 欣, 宋占伟. 动态图像的拼接与运动目标检测方法的研究[J]. 图学学报, 2014, 35(6): 893-898.

[13] 韩 凯, 庞宗强, 王 龙, 等. 基于深度扫描仪的高辨识度三维人体模型重建方法[J]. 图学学报, 2015, 36(4): 503-510.

[14] 于仕祺, 刘瑞祯. 学习 OpenCV[M]. 北京: 清华大学出版社, 2009: 406-438.

[15] 马颂德, 张正友. 计算机视觉: 计算理论与算法基础[M]. 北京: 科学出版社, 1998: 52-70.

A New Method for 3D Space Calibration Based on Planar Calibration Board

Wang Xiangdong, Dong Qiqi
(China Institute of Sport Science, Beijing 100061, China)

This paper puts forward a new 3D space calibration method by using planar checkerboard lattice calibration in based on the existing problems for using three-dimensional frame camera calibration in the calibration range, error, portable and aging aspects. This study selected five meters, ten meters and 30 meters of the shooting distance. Calibration reference object used traditional 3D radiation type stereo frame and homemade two-dimensional planar checkerboard calibration plate, the standard meter length scale for 3D reconstruction. The accuracy comparison of two kinds of measurement results is carried out. In addition, the error distribution of the different position of the standard one meter in the measurement space (the middle and the edge of the measuring frame) is carried out. Experimental results showed that implemented in this paper based on planar checkerboard calibration plate camera calibration method had significant advantages, regardless of convenience and measurement accuracy this new method was better than three-dimensional framework and met the needs of scientific research of physical education.

sports scientific research; sport biomechanics; three-dimensional framework; camera calibration; plane calibration

TP 391

10.11996/JG.j.2095-302X.2016060778

A

2095-302X(2016)06-0778-05

2016-02-29；定稿日期：2016-05-11

国家体育总局体育科学研究所基础业务费项目(基本14-02，基本15-02)

王向东(1973−)，男，山西太原人，研究员，博士。主要研究方向为运动生物力学与运动技术诊断。E-mail：wangxiangdong@ciss.cn