静应力对岩石波动参数的影响研究现状及新问题的思考
2017-01-19昌晓旭金解放
昌晓旭,金解放,程 昀,何 聪,袁 伟
(江西理工大学建筑与测绘工程学院,江西 赣州 341000)
矿业纵横
静应力对岩石波动参数的影响研究现状及新问题的思考
昌晓旭,金解放,程 昀,何 聪,袁 伟
(江西理工大学建筑与测绘工程学院,江西 赣州 341000)
各类工程岩体中普遍存在静应力,静应力对岩体材料特性的影响极其重要且不可忽略。通过对现有文献进行系统梳理与归纳总结发现静应力对岩石纵波波速有影响且纵波波速与密度有关系,但当前研究存在两个问题: 没有进一步分析静应力对岩石波阻抗的影响; 静应力主要是等值静应力。而工程岩体中的静应力多为梯度应力,梯度应力的存在导致岩体波阻抗呈梯度形式变化,因此针对深部工程岩体爆破开挖及地震波传播等,有必要开展具有梯度应力岩石中应力波传播衰减规律的相关研究。
静应力;波速;密度;波阻抗;梯度
各类岩体工程中普遍存在静应力,例如自重应力和构造应力,其所处的位置越深,所处的静应力状态越复杂[1-2]。复杂应力状态对工程岩体的力学特性有较大的影响[3-4]。众多研究表明,静应力对工程岩体材料特性的影响是极其重要且不可忽略的,是分析工程岩体破坏和稳定性的重要因素。在采矿领域,应力的存在就会表现出以冲击矿压、矿震为代表的灾害事故。为了研究这些事故的发生机理,尽量减少带来的损失,很多学者做出相应的研究[5-6]。在油田开发领域,储层具有渗透率应力敏感性,钻井取心过程中,应力状态由原始地应力状态变为井筒中泥浆的静水压力状态,使承载骨架颗粒与孔喉结构间的原始关系发生变化,这将直接影响油井的产能[7-8]。在水利水电工程领域,工程中面临的高地应力引起的结构安全、大变形等问题是近些年来水利工程领域岩石力学研究的热点和难点[9-10]。邬爱清等[11]总结了前人的研究成果,提出了如何考虑围岩变形破坏过程中岩体力学参数的变化过程,以及如何反映岩体的弹脆塑性力学行为的硬岩本构模型特别是峰值后应力下降段的力学行为等问题。在隧道工程建设领域,由于施工开挖引起的应力重分布超过围岩强度或引起围岩侧向变形较大致使岩体失稳[12]。贾剑青等[13]研究了复杂条件下隧道支护结构稳定性,结果表明二次衬砌能够及时调动围岩的自承能力,在一定程度上起到安全储备的作用,增加了结构的稳定性。这些研究成果为相应的岩体工程设计、施工及维护提供了理论依据。
由波动理论等可知,声波在岩石(体)介质中的传播波速、能量衰减以及频谱信息的变化,能反映介质的物理力学特性。因此声波测试技术在岩石(体)弹性参数测定、工程岩体无损检测、岩体稳定性评价及围岩地应力测量方面有较广泛的应用[14-16]。基于此,针对不同类型的岩体工程和不同类型的岩石,研究波速和岩石(体)所处的应力关系一直是岩石力学研究的热点问题。学者们[17-34]分别研究了砂岩、花岗岩、煤岩及其岩性的应力与波速的关系。范新等[35]研究了初始应力对应力波传播及块体运动规律的影响,得到了初始应力对质点运动状态和应力波传播过程中衰减特性的影响。金解放等[36]考虑了轴向静载荷的存在对入射波及岩石动态力学特性的影响。陶明[37]分析了高应力岩体的动态加卸荷扰动特征与动力学机理,阐述了初始应力对岩石中弹性波传播的影响。基于声波波速和介质密度大小都同时反映介质孔隙率大小的特性,部分学者通过理论和试验研究了介质波速和密度的关系。
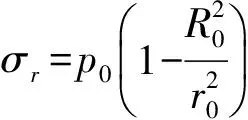
1 岩石波速与应力关系
众多学者对岩石的波动参数与静应力的关系做了大量研究,在实验的基础上得到了许多经验公式和模型。对于不同岩性的岩石或者同种岩石的不同状态下,岩石的应力状态不同,波动参数的变化也会不同。本文选取了花岗岩、灰岩、片麻岩等6种具有代表性的岩石,总结了前人得出应力对波速的影响研究成果。
1.1 花岗岩波速与应力关系
Brich[17-18]早在20世纪60年代就研究了花岗岩纵波波速随静水压力的变化(0~1.05GPa),研究表明岩石纵波波速随压力逐渐增大,当压力超过一定值以后,增大趋势减小,最终趋于平稳。Nur和Engelder等[19-20]通过研究发现,单轴加载时应力可以引起花岗岩中弹性波速的各向异性,沿受力方向压缩波传播速度最快,剪切波则沿各个方向都不相同,波速随应力的增加而增加,并且在平行于应力的方向要比垂直于应力的方向增加的程度要大。
蔡忠理等[21]在20世纪80年代对岩石应力应变过程中的声学特性进行了研究,基于自制的信号自动采集与处理系统,研究了花岗岩在单轴压缩过程中各种声学参数的变化规律及其与应力的关系。文献[21]针对新鲜的花岗岩和强风化花岗岩,通过试验拟合分别得出其纵波波速与应力关系见式(1)~(2)。
(1)
(2)
式中,σu为岩样的破坏应力,对于不同风化程度的花岗岩,σu也不同,风化程度越厉害,σu就越小,但是可以看出,两式的形式一样,说明不论花岗岩风化程度如何,在施加的应力达到其破坏应力之前,岩石的波速都会随着应力的增加而变大,强风化花岗岩波速的增加幅度更大,并且强风化花岗岩的波速远远小于新鲜花岗岩的波速,这是因为岩石的风化程度越高,内部的孔隙就越多,初始波速就越小,在受力后,波速变化的就越快。当施加的应力超过σu时,两种岩样的波速都会明显下降。
1.2 灰岩波速与应力关系
王宏图等[22]研究了灰岩三向应力状态下弹性波的传播特性,岩样取用重庆市嘉陵江微晶质灰岩,在试验中分别进行单轴加载和三轴加载,在加载过程中获得岩样的变形数据和波速,根据数据拟合所得公式见式(3)。
(3)
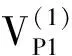
张清林等[23]研究了灰岩在单轴加荷过程中弹性波速的变化规律,其研究表明,岩石所受荷载增大,其内部不同方向上传播的弹性波速也随之增大,不同方向上增大的幅度不同:在靠近压力作用方向上,弹性波速度增加较大;在垂直于压力作用方向上,弹性波速度增加较小。在加载后期,不同方向的波速都急剧降低。
对于灰岩,王宏图和张清林都研究了应力对波速的影响。前者得出,灰岩应力对波速的影响与岩石的压密极限密切相关,波速与应力基本呈线性关系;后者得出,波速随应力先增后减,不同方向上波速随着应力的增大幅度不同。
1.3 片麻岩、闪长岩波速与应力关系
为了研究工程开挖导致的卸荷效应,陈祥等[24]研究了岩块在不同卸荷状态下波速与应力的关系,以青岛地区黄岛地下水封油库工程为例,对从现场取得的片麻岩和闪长岩,利用自行设计的试验装置进行岩石波速-应力关系试验,获得岩石在受荷过程中波速的变化情况,如图1所示。
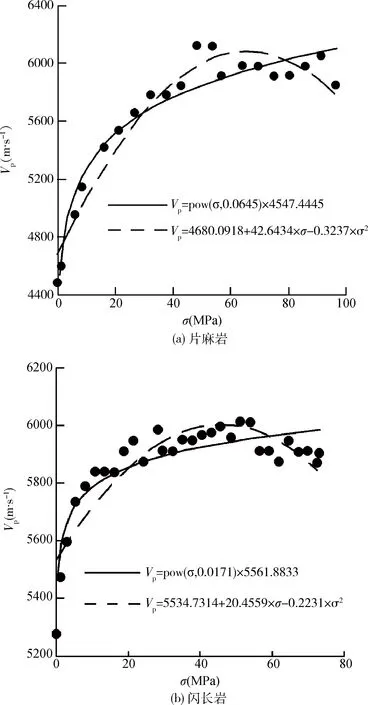
图1 片麻岩和闪长岩岩样波速与应力关系[24]
图1中,两种岩石在受压变形过程中波速始终变化,随着应力的增大纵波波速增大,说明应力对纵波波速有较大的影响。用幂函数和二次函数都可以较好地反映两种岩石的波速与应力关系。幂函数曲线随应力的增大,波速会一直变大,不会有变小的情况;二次函数曲线当应力超过一定的范围时,波速会随着应力的增大而减小,从实际情况来看,二次函数曲线与实际情况更吻合。
张建勇[25]研究了片麻岩在加载过程中波速变化情况,结果表明,完整岩石在单轴加载过程中,所加载荷达到其强度的60%~80%时,岩石产生裂纹,波速明显降低。带裂纹的岩石在加载初期波速就随荷载的增加而降低,之后波速在小范围内波动,直到岩石破坏。
对比两人的研究成果,陈祥给出了片麻岩和闪长岩应力与波速关系的两种拟合公式,张建勇进一步研究得出岩石在应力达到何种强度时,波速会降低。
1.4 砂岩波速与应力关系
Thill等[26-28]以砂岩为研究对象,从岩石中裂纹闭合的角度考虑,提出了岩石压密阶段波速随应力呈二次函数关系。Khaksar等[29]通过研究发现干燥的含气砂岩压缩波与剪切波波速与围压近似呈幂函数关系。宋丽莉等[30]根据疏松砂岩储层的地层应力条件建立了弹性波速测试系统,对储层岩样弹性波速进行了实验,研究发现波速与砂岩孔隙度、泥质含量、应力和温度都有关系,其中纵波波速与应力也呈幂函数关系,见式(4)。
(4)
李高勇[31]以引洮供水工程7#洞新近系砂岩为研究对象,系统研究了不同应力状态下试样的波速变化情况,根据应力和波速的测试结果,得到了砂岩在不同应力状态下的应力应变特征及波速特征,进而分析了波速与应力的实时同向相关性。通过多种应力加载与波速试验及对结果的分析,发现在各种应力状态下,砂岩的波速对应力改变具有很好的响应。确定了砂岩波速与应力的关系为线性相关,并取得了波速与应力的拟合公式,见式(5)。
VP=33.55σ+2379.89
(5)
刘向君等[32]研究了低孔低渗砂岩的声波传播特性,结果表明,砂岩在三轴和单轴加载过程中声波波速、幅度、频谱特性都会变化,具体表现为:波速随着应力的增大先增大后减小,在应力达到峰值强度前阶段,纵波首波振幅和频谱主振幅都表现出上升趋势,随着应力的进一步增大,频谱曲线上低频端较高频端活跃。
1.5 煤岩波速与应力关系
巩思园等[33-34]为了研究煤矿中冲击矿压现象的发生机理,利用单轴加载的方式,研究煤岩应力与纵波波速的关系,加工了多组煤岩试样,通过实验测出试样的应力值与波速值,建立二者之间的耦合关系,见式(6)。
(6)
式中,φ和Ψ为拟合参数。
通过对不同煤岩试样的试验,发现φ由试样开始加载时的波速值决定,为无载荷下的波速值,与应力无关,是试样的固有属性;Ψ与加载过程中波速上升的快慢有关,它体现波速对应力的敏感程度,Ψ值越大,波速上升就越快,反之越慢。由拟合结果可以看出,在应力作用的开始阶段,煤岩试样的纵波波速变化较大,随着应力的不断增加,纵波波速的上升幅度变小,并逐渐趋于水平。在应力升高到一定阶段后,影响波速的因素不再随应力的增加而变化。
1.6 岩石波速与应力相关性的机理分析
上述研究表明,应力对波速有影响,不同岩性的岩石影响不同,同种岩石不同应力下,对波速的影响效果也不同。早有研究发现波速变化的实质是岩石内部裂隙的变化[38-41],由此可知,岩石波速随应力的变化与两方面因素有关。
其一,与岩石内部裂隙状态有关。岩石内部裂隙可以是圆形、方形、椭圆形等任何形状,可以水平分布、垂直分布、交叉分布等任何分布形式,裂隙的尺寸和开度大小也不确定,因此,不同形状不同分布不同尺寸不同开度的裂隙在受到同样应力的作用时,对应力的响应也不同。例如,对于开度极小的椭圆形裂隙来说,其倾角较小时,在较低的应力下就发生闭合,闭合应力随着裂隙倾角的增加而增大,当裂隙倾角接近90°时,裂隙就难以闭合。
其二,与施加的应力大小和方向有关。对于同一块岩石来说,其内部裂隙的闭合就只与应力有关。在初始阶段,岩石中大部分裂隙在低应力下就发生闭合,波速显著增大;随着应力的增加,岩石在闭合旧裂隙的同时逐渐产生新裂隙,在此阶段,波速基本不变;当应力更大时,产生的新裂隙数量多于闭合旧裂隙的数量,岩石发生破坏,波速迅速降低。此外,应力作用方向不同,岩石裂隙的闭合效果也不同。当应力作用方向垂直于裂隙时,裂隙在较低的应力下就能闭合,随着应力与裂隙夹角的缩小,裂隙的闭合难度就增加,当应力方向平行于裂隙时,裂隙就很难闭合。
前人的研究成果表明岩石应力与波速关系用线性函数、幂函数和二次函数都能拟合,根据上述分析可知,应力处于不同阶段,三种拟合曲线的精度不同。在初始阶段,应力与波速关系用线性拟合效果更好;在稳定阶段,幂函数能更好的反映应力与波速关系;在破坏阶段,二次函数最能描述应力与波速关系。这也是为什么即使对于同一种岩石,却有不同拟合关系的原因。
2 岩石密度与波速关系
从文献发现,直接研究应力大小对岩石(体)密度影响的研究较少。但有学者研究了密度随波速变化而变化的规律。
Gardner等[42]早在1974年就通过测试大量盐水饱和岩石的波速和密度数据,统计结果显示波速和密度间的关系可表示为式(7)。
(7)
式中:密度ρ,g/cm3;纵波速度VP,m/s。式(7)具有很好的适用性,至今仍在地震资料数字处理和研究中广泛应用。
朱广生等[43]在Gardner研究成果的基础上,认为Gardner得到的经验公式只适用于特定的岩层和环境下,该公式没有对中国地层的适用性做过研究,因此,采用大庆油田声波测井和密度测井数据,所得数据的测量井段的岩性为砂岩、泥岩、钙质砂岩、钙质泥岩及碳酸盐岩,其中主要是砂岩和泥岩。此外,少数井段为含油气地层。以此为工程背景,对数据进行统计分析得出密度和波速的关系如图2所示。图2中D表示岩石的密度。对图2中曲线进行拟合,得到拟合公式,见式(8)。
(8)
对比式(7)和式(8)可以看出,两式的形式相同,说明Gardner得到的密度与波速的关系是合理的,只有朱广生得到的结果可能更适合中国的地层。
孟召平等[44-45]在2006年提出了对煤系沉积岩石力学参数与波速的关系进行研究,选取5个矿区的164块岩样进行声波速度实验,对大量的实验数据进行分析整合,最终得到密度与纵波波速间的函数关系,如图3所示。
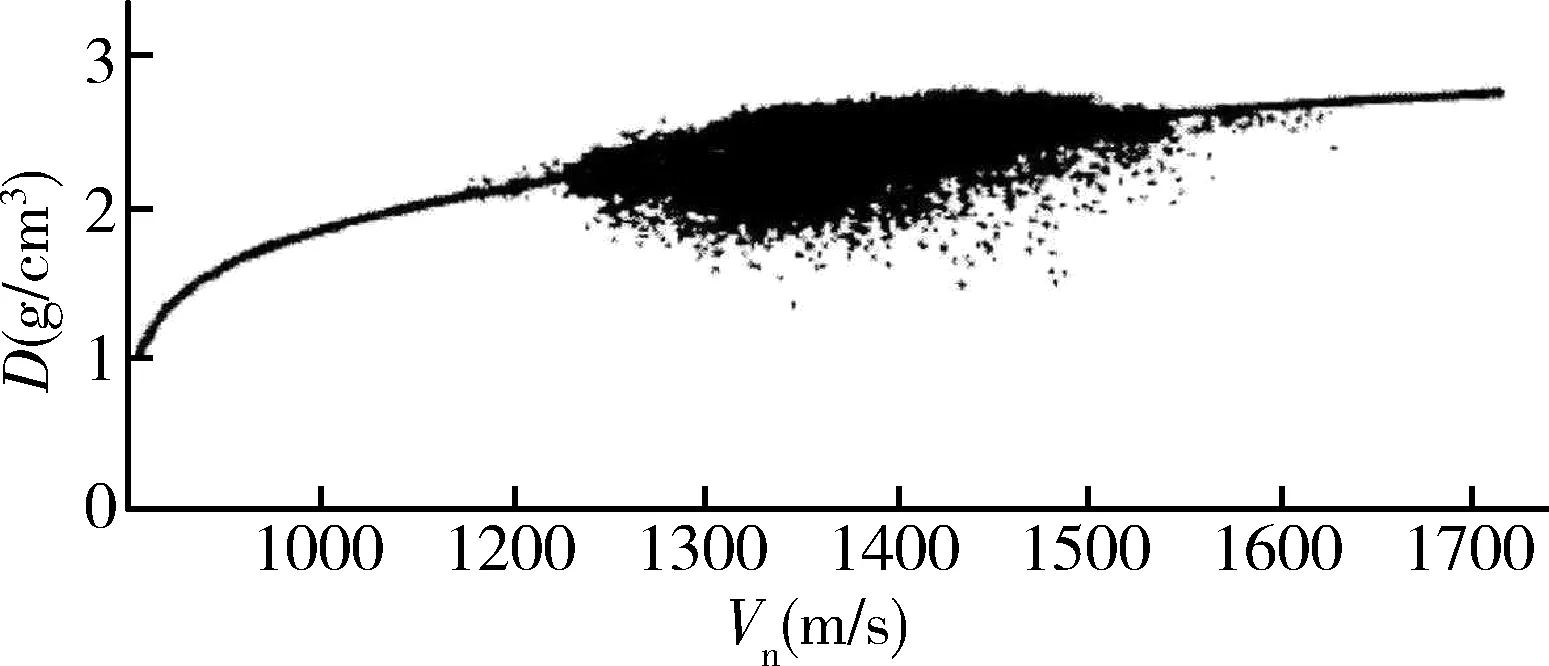
图2 声波测井和密度测井得出的密度和纵波波速的关系[43]

图3 煤系岩石的密度和纵波波速的关系[44]
由图3看出,煤系沉积岩密度与波速的关系拟合结果为二次函数关系,这与Gardner和朱广生研究所得幂函数关系不相同,主要是因为煤系沉积岩石岩性较为软弱,变化较大,成分和结构复杂,以至于其密度与声波速度的关系没有像其岩石一样。
李月等[46]认为许多学者在岩石声学特性方面的研究多以单一岩石为研究对象,而地基工程中常常遇到层状岩体问题,因此研究了地基层状岩石波速与密度的关系。首先测出玄武岩、花岗岩和石灰岩三种岩样的纵波波速,接着把三种岩石用502粘结剂粘接,再测试了层状岩的纵波波速,最后分别研究了单一岩石和层状岩的密度和纵波波速的关系,对试验结果进行回归分析,得到玄武岩、花岗岩、石灰岩和层状岩的关系式分,别见式(9)~(12)。
VP1=219078ρ1-312764
(9)
VP2=216261ρ2-312016
(10)
VP3=218257ρ3-311155
(11)
VP4=2145ρ4-21486
(12)
由式(9)~(12)看出,不论是单一的岩石还是层状岩,波速都会随着密度的增加而变大,但是增加的幅度有所不同,玄武岩增加幅度最大,其次是石灰岩,再次是花岗岩,层状岩最小,也就是说,玄武岩密度的变化对纵波波速的影响最大,而层状岩最小。该拟合结果为线性关系,与幂函数和二次函数关系不同,主要是因为所取的波速值范围不同,在岩石常见波速变化范围内,岩石密度与波速是呈线性相关关系的。
通过上述分析,可以发现,前人通过实测数据拟合得出的岩石密度和波速关系的形式不同,即Gardner、朱广生得出密度与波速呈幂函数关系,孟召平得出密度与波速呈二次函数关系,李月得出密度与波速呈线性函数关系,说明岩石的岩性不同,所处环境不同,密度和波速的关系可能也不同,但都能说明岩石波速与密度间具有良好的正向相关性。
综合前面分析可知,随着应力的增大,波速增大,密度增大,进而可得,应力增大,密度增大,即应力与密度也具有正向相关性,这也说明了为什么能用波速进行无损检测。
3 讨 论
3.1 岩石应力对波阻抗的影响
根据前文可知,不论岩石所处状态如何,岩性是否相同,其内部应力与波速、波速与密度都有关系,虽然即使是同一种岩石,所施加的应力不同,上述关系也不尽相同,但都以三种形式存在,即线性关系、幂函数关系和二次函数关系。在地震波传播的研究中,岩石的波阻抗ρC是密度ρ和波速C的乘积(波速C即前面提到的纵波波速VP),由上述分析已知,应力与波速和密度都有关系,那么应力与波阻抗也必然有关系。若应力与波速为线性关系,波速与密度为幂函数关系,应力与波阻抗是何种关系;再比如应力与波速为二次函数关系,波速与密度为线性关系,应力与波阻抗关系又如何。以此类推,可知,应力与波阻抗也会存在多种关系,即应力对岩石波阻抗的影响十分复杂。
3.2 梯度应力对应力波传播的影响
上述结果表明,静应力对岩石的波阻抗有影响。基于应力波理论及以上分析可知,对于等波阻抗的弹性介质,应力波在其中传播时无衰减、无频散、无变速现象,当具有梯度应力时,梯度应力将使材料的等值波阻抗变为非等值波阻抗,应力波在变化波阻抗的材料中传播时,在波阻抗不等的界面两侧必然会发生透反射,如此一来,应力波在传播过程中,幅值、波形、频率、相位等必然发生变化。那么材料具有的梯度应力对应力波传播的影响是高频波发生衰减,还是由于不同频率的波在波阻抗变化处多次透反射引起的传播速度不同。这个问题的解决有利于深入研究梯度应力对应力波传播衰减特性的影响。
此外,目前描述应力波在介质中传播衰减特性的参数较多,例如量化应力波幅值随传播距离衰减的吸收系数,量化应力波幅值随传播时间衰减的衰减系数、对数衰减率和品质因子等[47-52]。就品质因子而言,其定义方法又有两大类:时域内建立和频域内建立。这些方法各有优缺点,不同方法表征应力波传播衰减的现象不同,应用的条件也不同,因此在研究具有梯度应力岩石中应力波传播衰减特性时,选择表征应力波传播衰减的合理有效参数是另一个值得探讨的问题。
4 结 语
本文论述了不同岩性的岩石中应力对波速的影响以及波速与密度关系的研究现状,进而,讨论了应力与波阻抗的关系,阐明了研究梯度应力的存在对应力波传播影响的重要意义,得出如下结论。
1)岩石中静应力的存在对波速有影响,岩石岩性不同,应力大小不同,波速的变化也不同。总体来说,波速随应力的变化分为三个阶段,即先增大再趋于平缓后减小。
2)岩石的密度与波速有关系,岩石的密度越大,波速越大,二者之间具有正向相关性。
3)工程围岩体中的静应力多为梯度应力,梯度应力的存在导致围岩体的波阻抗也成梯度形式变化(线性梯度或非线性梯度),针对不同岩性岩石在不同情况下波阻抗的变化规律值得进行研究。
4)与应力波在具有等值波阻抗岩石中的传播规律研究相比,应力波在具有不同梯度应力岩石(体)中的传播规律研究处于空白状态,因此在工程岩体爆破开挖围岩体稳定性分析及地震波传播等相关领域研究急需开展相关研究,比如不同岩性岩石在不同梯度应力情况下的传播衰减规律,以及针对不同情况选择哪种参数量化应力波传播衰减的时空规律等。
[1] 李新平,赵航,罗忆,等.深部裂隙岩体中弹性波传播与衰减规律试验研究[J].岩石力学与工程学报,2015,34(11):2319-2326.
[2] 侯明勋.深部岩体三维地应力测量新方法、新原理及其相关问题研究[J].岩石力学与工程学报,2004,23(24):4258.
[3] 王明洋,周泽平,钱七虎.深部岩体的构造和变形与破坏问题[J].岩石力学与工程学报,2006,25(3):448-455.
[4] 孟召平,李明生,陆鹏庆,等.深部温度、压力条件及其对砂岩力学性质的影响[J].岩石力学与工程学报,2006,25(6):1177-1181.
[5] 陆菜平,窦林名,曹安业,等.深部高应力集中区域矿震活动规律研究[J].岩石力学与工程学报,2008,11:2302-2308.
[6] 巩思园.矿震震动波波速层析成像原理及其预测煤矿冲击危险应用实践[D].徐州:中国矿业大学,2010.
[7] 李转红,任晓娟,张宁生,等.特低渗储层应力敏感性及对油井产量的影响[J].西安石油大学学报:自然科学版,2005,20(4):60-63.
[8] 于忠良,熊伟,高树生,等.致密储层应力敏感性及其对油田开发的影响[J].石油学报:2007,28(4):95-98.
[9] 钱七虎.非线形岩石力学的新进展―深部岩体力学的若干关键问题[C]//第八次全国岩石力学与工程学术会议论文集.北京:科学出版社,2004:10-17.
[10] 王思敬.中国岩石力学与工程的世纪成就与历史使命[J].岩石力学与工程学报,2003,22(6):867-871.
[11] 邬爱清,朱杰兵.深部岩石工程力学特性及地应力测试研究综述[J].长江科学院院报,2014,31(10):43-50.
[12] 邵国建,卓家寿,章青.岩体稳定性分析与评判准则研究[J].岩石力学与工程学报,2003,22(5):691-696.
[13] 贾剑青,王宏图,李 晶,等.复杂条件下隧道支护结构稳定性分析[J].岩土力学,2010,31(11):3599-3603,3618.
[14] 赵明阶.裂隙岩体在受荷条件下的声学特性研究[J].岩石力学与工程学报,1999,02:120.
[15] 宋战平,王军祥,姜谙男,等.单轴压缩状态下饱水裂隙片岩超声试验研究[J].岩石力学与工程学报,2014(12):2377-2383.
[16] 李彪,戴峰,徐奴文,等.深埋地下厂房微震监测系统及其工程应用[J].岩石力学与工程学报,2014(S1):3375-3383.
[17] Birch F.The velocity of compressional waves in rocks to 10 kilobars,Part 1[J].Journal of Geophysical Research,1960,65(4):1083-1102.
[18] Birch F.The velocity of compressional waves in rocks to 10 kilobars,Part2[J].Journal of Geophysical Research,1961,66(7):2199-2224.
[19] Nur A,Simmons G. Stress-induced velocity anisotropy in rock:An experimental study[J].Journal of Geophysical Research,1969,74(27):6667-6674.
[20] Engelder T,Plumb R.Changes in in situ ultrasonic properties of rock on strain relaxation[J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1984,21(2):75-82.
[21] 蔡忠理,刘克,吴绵拔,等.单轴压缩过程中花岗岩的声学特性研究[J].岩土力学,1986,7(2):27-36.
[22] 王宏图,鲜学福.复杂应力状态下岩石弹性波传播特性的研究[J].重庆大学学报:自然科学版,1988(5):52-59.
[23] 张清林,孙进忠,王海峰,等.岩石试块单轴加荷过程中弹性波速变化规律的试验研究[J].实验室科学,2011(6):100-106.
[24] 陈祥,孙进忠,谭朝爽,等.岩块波速-应力关系及其卸荷效应[J].岩土工程学报,2010,32(5):757-761.
[25] 张建勇.岩石加载过程中的波速及其声发射特征研究[D].沈阳:东北大学,2008.
[26] Thill R E,Bur T R,Steckley R C.Velocity anisotropy in dry and saturated rock spheres and it elation to rock fabric[J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts,1973,10(6):535-557.
[27] Nur A.Effects of stress on velocity anisotropy in rocks with cracks[J].Journal of Geophysical Research,1971,76(8):2022-2034.
[28] Su W H,Peng S S,Okubo S,et al.Development of ultrasonic methods for measuring in-situ stresses at great depth[J].Mining Science and Technology,1983,1(1):21-42.
[29] Khaksar A,Griffiths C M,Mccann C.Compressional and shear-wave velocities as a function of confining stress in dry sandstones[J].Geophysical Prospecting,1999,47(4):487-508.
[30] 宋丽莉,葛洪魁,王宝善.疏松砂岩弹性波速的实验研究[J].测井技术,2004(6):487-490,566.
[31] 李高勇.砂岩的波速与应力实时同向相关性研究[D].兰州:兰州大学,2012.
[32] 刘向君,刘洪,徐晓雷,等.低孔低渗砂岩加载条件下的声波传播特性实验研究[J].岩石力学与工程学报,2009,28(3):560-567.
[33] 巩思园,窦林名,徐晓菊,等.冲击倾向煤岩纵波波速与应力关系试验研究[J].采矿与安全工程学报,2012,29(1):67-71.
[34] 巩思园,窦林名,何江,等.深部冲击倾向煤岩循环加卸载的纵波波速与应力关系试验研究[J].岩土力学,2012,33(1):41-47.
[35] 范新,王明洋,施存程.初始应力对应力波传播及块体运动规律影响研究[J].岩石力学与工程学报,2009,28(S2):3442-3446.
[36] 金解放,李夕兵,尹土兵,等.轴向冲击下弹性杆中轴向静载对入射波的影响[J].工程力学,2013,30(11):21-27.
[37] 陶明.高应力岩体的动态加卸荷扰动特征与动力学机理研究[D].长沙:中南大学,2013.
[38] Anderson D L,Minster B,Cole D.The effect of oriented cracks on seismic velocities[J].Journal of Geophysical Research,1974,79(26):4011-4015.
[39] Sayers C M.Inversion of ultrasonic wave velocity measurements to obtain the microcrack orientation distribution in rocks[J].Ultrasonic,1988,26(3):73-77.
[40] Hu K X,Huang Y.Estimation of the elastic properties of fractureed rock mass[J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts,1993,30(4):381-394.
[41] Holt R T.Stress dependent wave velocities in sedimentary rock cores:Why and why not[J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts,1997,34(3):261-276.
[42] Gardner G H F,Gardner L W.Formation velocity and density-the diagnostic basics for strati graphic traps[J].Geophysics,1974,39:770-780.
[43] 朱广生,桂志先,熊新斌,等.密度与纵横波速度关系[J].地球物理学报,1995,38(S1):260-264.
[44] 孟召平,张吉昌,Joachim Tiedemann.煤系岩石物理力学参数与声波速度之间的关系[J].地球物理学报,2006,49(5):1505-1510.
[45] 孟召平,刘常青,贺小黑,等.煤系岩石声波速度及其影响因素实验分析[J].采矿与安全工程学报,2008,25(4):389-393.
[46] 李月,刘立,李玉梅,等.地基层状岩石纵波波速与密度相关性试验研究[J].四川建筑科学研究,2009,35(1):125-171.
[47] 喻振华,冯德山,汤井田.地震波速与吸收系数综合层析成像[J].地球物理学进展,2006,21(4):1338-1341.
[48] 王观石,李长洪,胡世丽,等.岩体中应力波幅值随时空衰减的关系[J].岩土力学,2010,31(11):3487-3492.
[49] Causse E,Mittet R,Ursin B.Preconditioning of full-waveform inversion in viscoacoustic media[J].Geophysics,1999,64(1):130-145.
[50] Wang H Z,Zhang L B,Ma Z T.Seismic wave imaging in visco-acoustic media[J].Science in China,Ser A,2004,47(S1):146-154.
[51] 王炳辉,陈国兴.循环荷载下饱和南京细砂的孔压增量模型[J].岩土工程学报,2011,33(2):188-194.
[52] 李生杰,施行觉,叶林,等.准葛尔盆地岩石品质因子与速度分析[J].内陆地震,2001,15(3):224-231.
Research on the effect of static stress on rock fluctuating parameters and consideration of new problems
CHANG Xiaoxu,JIN Jiefang,CHENG Yun,HE Cong,YUAN Wei
(School of Architectural and Surveying Engineering,Jiangxi University of Science and Technology,Ganzhou 341000,China)
Static stress is prevalent in all kinds of engineering rock mass, and the influence of static stress on the characteristics of rock mass is very important and can not be ignored. By combing the existing literature systematically, we found that the static stress has an effect on longitudinal wave velocity of rock and longitudinal wave velocity and density are related, but the current study there are two problems: no further analysis of the influence of static stress on the wave impedance of rock; static stress is mainly uniform static stress. But the static stress in the engineering rock mass is mostly gradient stress, the gradient stress leads to the change of the wave impedance of the rock mass in the form of gradient. In view of the blasting excavation of deep rock mass and the seismic wave propagation, the effect of gradient stress in rocks on the law of the propagation and attenuation of stress wave needs further studies.
static stress;wave velocity;density;wave impedance;gradient
2016-03-17
国家自然科学基金项目资助(编号:51104068;51664017);江西省自然科学基金资助(编号:20151BAB206025); 江西省教育厅科技项目资助(编号:gjj14462)
昌晓旭(1992-),男,汉,河南信阳人,硕士研究生,主要从事岩石动力学及岩体稳定性分析方面的研究,E-mail:1448993484@qq.com。
金解放(1977-),男,博士,副教授,主要从事岩石动力学及岩体稳定性分析方面的教学和科研工作,E-mail:jjf_chang@126.com。
TD353
A
1004-4051(2016)12-0121-07
