一类函数方程周期解周期的确定

宋泽熙， 周铁军

(湖南农业大学东方科技学院，长沙410128)



一类函数方程周期解周期的确定

宋泽熙， 周铁军

(湖南农业大学东方科技学院，长沙410128)

研究了函数方程af(x+T1+T2)+bf(x)=af(x+T1)+bf(x+T2)在两种情形下解的周期，获得的结果推广了已有结论.

函数方程； 周期解； 周期

1 引 言

函数方程及其周期解的性质一直是学者关注的研究内容[1-4]，文献[1]中讨论了如下特殊形式的函数方程

f(x+T1+T2)+f(x)=f(x+T1)+f(x+T2) ，

(1)

其中T1，T2是常数，且存在整数m，n使得nT1=mT2=T，作者证明了满足方程(1)的函数是周期为T的周期函数.本文将上述方程推广为如下一般形式的函数方程

af(x+T1+T2)+bf(x)=af(x+T1)+bf(x+T2),

(2)

2 主要结论

证由(2)式可得

af(x+T1+T2)-bf(x+T2)=af(x+T1)-bf(x).

(3)

记F(x)=af(x+T1)-bf(x),则由(3)式得F(x+T2)=F(x),即F(x)是周期为T2的函数，则它也是周期为mT2=T的周期函数，从而有F(x+T)=F(x)，即有

af(x+T1+T)-bf(x+T)=af(x+T1)-bf(x)，

于是有

(4)

类似地有

由于nT1=T，得

于是又有

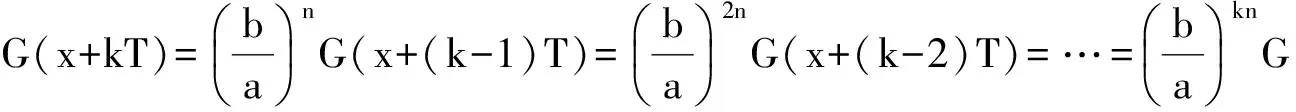
根据G(x)的定义，从上式得

所以

从而可得

所以

定理2设f(x)是实数域上的有界函数，且存在整数m,n使得nT1=mT2=T，其中T1,T2是满足(2)的常数.如果a=-b≠0，则当n是偶数时，满足方程(2)的函数f(x)是周期为T的周期函数；当n是奇数时，满足方程(2)的函数f(x)是周期为2T的周期函数.

证当a=-b≠0时，(2)式可化为得

f(x+T1+T2)-f(x)=f(x+T1)-f(x+T2).

(5)

于是得

f(x+T1+T2)+f(x+T2)=f(x+T1)+f(x).

记F(x)=f(x+T1)+f(x)，则有F(x+T2)=F(x)，因此F(x)是周期为T2的函数，则它也是周期为mT2=T的周期函数，从而有F(x+T)=F(x)，即有

f(x+T1+T)+f(x+T)=f(x+T1)+f(x).

于是有

(6)

由于也有F(x+2T)=F(x)，同理可得

(7)

(i)如果n是偶数，则定义函数G(x)=f(x+T)-f(x)，则由(6)式得G(x+T1)=-G(x)，于是得

G(x+2T1)=G(x).

考虑到n是偶数，则有G(x+nT1)=G(x)， 由于nT1=T，得

G(x+T)=G(x).

于是根据G(x)的定义，对任意正整数k，从上式得

G(x+kT)=f(x+kT+T)-f(x+kT)=G(x)，

所以

f(x+(k+1)T)=G(x)+f(x+kT).

从而可得

f(x+(k+1)T)=(k+1)G(x)+f(x).

(ii)如果n是奇数，则定义函数H(x)=f(x+2T)-f(x)，则由(7)式得H(x+T1)=-H(x)，于是得

H(x+2T1)=H(x).

从而有H(x+2nT1)=H(x)， 由于nT1=T，得

H(x+2T)=H(x).

于是根据H(x)的定义，对任意正整数k，从上式得

H(x+2kT)=f(x+2kT+2T)-f(x+2kT)=H(x)，

所以

f(x+2(k+1)T)=H(x)+f(x+2kT).

从而可得

f(x+2(k+1)T)=(k+1)H(x)+f(x).

3 举 例

下面举例说明上述定理的应用.

例1若函数 f(x)(x∈R)满足f(x)=f(x+T)+f(x-T),则f(x)是周期为6T的函数.

证由条件f(x)=f(x+T)+f(x-T),则有f(x+T)=f(x+2T)+f(x),两式相加得

f(x+2T)=-f(x-T)，

从而有f(x+3T)=-f(x)，f(x+4T)=-f(x+T).从而得到

f(x+4T)-f(x)=f(x+3T)-f(x+T).

即有

f(x+T1+T2)-f(x)=f(x+T1)-f(x+T2)，

其中T1=3T,T2=T.所以存在n=1,m=3，使得nT1=mT2=3T.注意到n=1是奇数，从而知f(x)是周期为2×3T=6T的函数.

注1 在例1中进一步可得到：f(x+5T)=-f(x+2T).从而得到

f(x+5T)-f(x)=f(x+3T)-f(x+2T).

即有

f(x+T1+T2)-f(x)=f(x+T1)-f(x+T2)，

其中T1=3T,T2=2T.所以存在n=2,m=3，使得nT1=mT2=6T.注意到n=2是偶数，根据定理2也可以得f(x)是周期为6T的函数.进一步还可以得：f(x+6T)=-f(x+3T).从而得到

f(x+6T)=-f(x+3T)=f(x)，

这样直接验证了f(x)是周期为6T的函数.

[1] 吴玫华.周期函数Fourier级数展开式唯一性的简单证明与推广[J].大学数学,2006,22(4):151-153.

[2] 谭福锦,农吉夫.复周期函数的若干性质[J].大学数学,2008,24(3):148-151.

[3] Ronald E.Mickens.Periodic solutions of the functional equation f2(t)+g2(t)=1 [J].Journal of Difference Equations and Applications, 2016, 22(1):67-74.

[4] 王立洪.一类由函数方程确定的周期函数[J].大学数学,2010,26(4):178-180.

Determination of Periodic Solutions of a Class of Function Equations

SONGZe-xi,ZHOUTie-jun

(Orient Science & Technology College of Hunan Agricultural University, Changsha 410128, China)

The period of solution for the functional equationaf(x+T1+T2)+bf(x)=af(x+T1)+bf(x+T2) is obtained.The results generalize the existing conclusions.

functional equation; periodic solution; period

2016-07-12； [修改日期]2016-09-07

湖南省科技计划项目(2015JC3101)

宋泽熙(1996-),男，本科在读，工程管理专业.Email: 2112105395@qq.com

周铁军(1965-)，男，博士，教授，从事生物数学研究.Email：hntjzhou@126.com

O13

C

1672-1454(2016)06-0087-04