随机变量绝对值的期望不等式
2017-01-18胡晓山廖俊俊
吴 娟, 胡晓山, 廖俊俊
(华中科技大学数学与统计学院,武汉430074)
随机变量绝对值的期望不等式
吴 娟, 胡晓山, 廖俊俊
(华中科技大学数学与统计学院,武汉430074)
在任意两个随机变量独立同分布的条件下,得到有关绝对值的数学期望不等式,并利用测度论给予完整证明.
数学期望; 独立同分布; 半正定; 绝对值
1 引 言

成立.同时给出了等号成立的充分条件,假设随机变量的期望均存在.为了处理随机变量绝对值的期望计算问题,本文利用矩阵论和测度论理论给予正面的解答.
2 主要结论
引理设∀xi,yi∈,i=1,2,…,n,有
(1)
证
其中sgn(x)是符号函数.
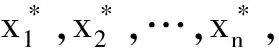
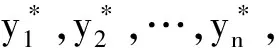
(2)
(2)式可看成一个二次型,所对应的实对称矩阵为

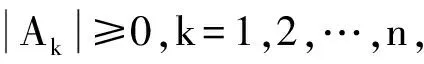
定理设任意两个随机变量X和Y独立同分布,则
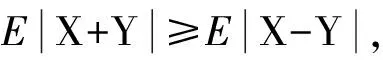
(3)
且等号成立的充分条件是X和Y均关于0是对称分布,假设(3)式中随机变量的期望均存在.
证先考虑X和Y是独立同分布的离散型随机变量,概率分布列为
由引理
故(3)式成立.
下面证明对任意随机变量X和Y,在独立同分布的条件下(3)式依然成立.
随机变量X是给定概率场上的有限可测函数[1],取此概率场上的函数序列{Xn,n=1,2,…},
(4)


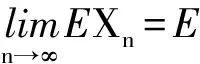
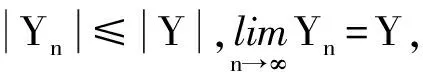
(5)
对(5)式取极限,由Lebesgue控制收敛定理,对任意随机变量X和Y,若满足独立同分布的条件,则

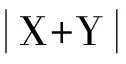

3 应用举例
在概率论课程教学[2,3]中,利用具体的概率分布举例说明期望不等式的作用.
例1设随机变量X和Y独立同分布,等可能地取区间[1,N]内的整数值,其中N是大于1的整数,则
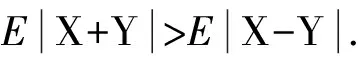
证
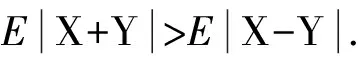

证
由例1的结论得
或直接积分得
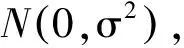

证
令x=ρcosθ,y=ρsinθ,
同理
若直接利用本文期望不等式定理,无需上例中的繁琐计算即可得结果.
[1] Kallenberg O.Foundations of Modern Probability[M].2nd ed., New York: Springer, 2002.
[2] 徐静.概率论教学中思维品质的培养[J].大学数学,2011,27(5):200-202.
[3] 边家文,付丽华,彭惠明,陆建华,邢婧,方秉武.概率统计课程中研究性学习方法探讨[J].大学数学,2012,28(2):11-15.
Expectation Inequality of Absolute Value of Random Variables
WUJuan,HUXiao-shan,LIAOJun-jun
(School of Mathematics and Statistics, Huazhong University of Science and Technology, Wuhan 430074, China)
This paper presents an expectation inequality of absolute value of any two random variables if they are independent and identically distributed.The approach is proved completely by the measure theory.
mathematical expectation; independent and identically distributed; positive semi-definite; absolute value
2016-06-27; [修改日期] 2016-07-22
国家自然科学基金(11171122);华中科技大学自主创新研究基金(2014QN083);华中科技大学教师教学能力培训项目(1501)
吴娟(1974-),女,博士,讲师,从事数理统计研究.Email:wujuan@hust.edu.cn
廖俊俊(1973-),男,博士,讲师,从事随机分析研究.Email:liaojunjun@hust.edu.cn
O211.5
C
1672-1454(2016)06-0079-04
