多个淹没水平圆柱诱发高阶谐波特性的数值与试验研究

李庆昕，宁德志*，滕斌

(1. 大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024)



多个淹没水平圆柱诱发高阶谐波特性的数值与试验研究

李庆昕1，宁德志1*，滕斌1

(1. 大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024)

基于势流理论采用时域高阶边界元方法建立了模拟非线性波浪与淹没水平双、三圆柱作用的数值水槽模型，其中采用混合欧拉-拉格朗日方法更新自由水面，四阶Runga-Kutta方法进行时间步进。利用两点法分离得到潜体下游高阶自由波，进而研究潜体间距、布置形式等对高倍频自由波的影响。同时在物理水槽内开展多潜体高阶谐波物理模型试验，并将试验结果与数值结果进行对比，吻合较好。研究发现：淹没双圆柱下游高阶谐波幅值随潜体间距呈现周期性振荡变化，其振荡的重现距离约为波长一半。而淹没三圆柱下游的高阶谐波随第一个间距呈周期性振荡变化，随第二个间距的增大而减小。

非线性数值水槽；多潜体；高阶谐波；物理模型试验；高阶边界元法

1 引言

潜体是常见的海洋工程结构物，且多潜体经常同时存在，如海底暗礁、石油和天然气输送管道等设施，应用十分广泛。波浪与多潜体作用后，由于潜体上方水深突然变浅，波浪非线性增强，产生与基频波同速度传播的高阶谐波，导致波能从低频分量向高频分量转换，从而改变了波浪的能量谱。当波浪传播至堤后，由于水深增大，波浪的非线性作用相对减弱，部分高阶谐波由锁相波释放为自由波。堤后产生的高阶自由波有可能影响通航条件，甚至对堤后海岸建筑物造成破坏，因此有必要对多潜体诱发高阶自由波特性开展深入研究。

许多学者已对波浪与潜体的相互作用问题进行了大量的理论分析、实验和数值模拟研究。在理论分析方面，Patarapanich[1]基于线性势流理论得到淹没水平板反射系数随板长与波长的比值呈振荡现象。在波浪与潜体作用的实验模拟方面，Dick和Brebner[2]通过试验发现了淹没水平板的下游存在高阶谐波；Grue[3]对波浪与淹没水平圆柱相互作用进行试验研究，并提出两点法分离高阶自由波和锁相波，发现在背浪侧，二阶自由波的幅值随着入射波幅值增大而增大，最大达到入射波幅的60%，在达到饱和值后逐渐减小。Brossard等[4]分析了非线性波浪与水平板相互作用诱发的水波共振现象，发现一阶共振与板长和板上方基频波波长的比值相关，二阶共振与板长和板上方锁相波长的比值相关，而反射系数与板前后基频波的相位差有一定的对应关系。此外，对于波浪与潜体相互作用的数值模拟方面，Ohyama和Nadaoka[5]利用边界元数值水槽对波浪与淹没台阶的相互作用进行模拟，发现当台阶的长度接近高阶谐波拍长一半时，在透射波中相应高阶谐波幅值会达到最大。郑永红等[6]利用改进的Boussinesq方程，对淹没潜堤上方的波浪变形进行了数值模拟，得到了波浪在潜堤上传播时波面演化过程；张洪生等[7]建立了一种以新型Boussinesq型方程为控制方程组的非线性波传播数学模型，与Luth等[8]的潜堤模型实验结果进行比较，其精度明显高于传统Boussinesq方程的精度；陈丽芬等[9]运用高阶边界元方法对波浪与潜堤相互作用问题进行研究，发现潜堤后的基频波、二阶和三阶自由波幅值分别与入射波幅成线性、二次和三次函数关系。Ning等[10]通过数值模拟研究水流对淹没圆柱诱发高阶谐波特性的影响。

上述大多研究仍集中在波浪与单潜体的相互作用问题上，而对实际中经常出现的多潜体诱发高阶谐波问题的研究还较少。本文分别以淹没水平双圆柱、三圆柱为潜体代表，采用非线性时域高阶边界元方法和物理模型实验进行模拟分析，运用两点法分离得到多潜体下游各阶锁相波和自由波。通过数值模拟结果与试验结果对比，验证模型准确性。进而开展数值试验分析强非线性条件下，高阶自由谐波幅值随多潜体系统布置形式、间距等因素的变化规律。

2 数学模型

2.1 控制方程和边界条件

考虑波浪与多淹没水平圆柱相互作用问题，如图1所示。建立二维笛卡尔坐标系xOz，原点O位于水槽左端，z=0位于静水面，z轴向上为正，x轴向右为正。图中，h表示静水深，hs(i)(i=1, 2, 3)分别表示各个潜体淹没水深(即从结构物最上端到静水面的距离)，s表示两个淹没结构之间的间距，r表示圆柱半径，ΓI表示入射边界，ΓF为自由水面边界，ΓO为出流边界，ΓB为水底和物面边界，Ω表示整个流域。考虑问题一般性，本文中假定各个潜体形状、特征长度和淹没深度均相同。在流体无黏、不可压缩和流动无旋的假定下，则势流理论可以应用于整个计算域内，存在速度势φ满足控制方程Laplace程：

▽2φ=0，

(1)

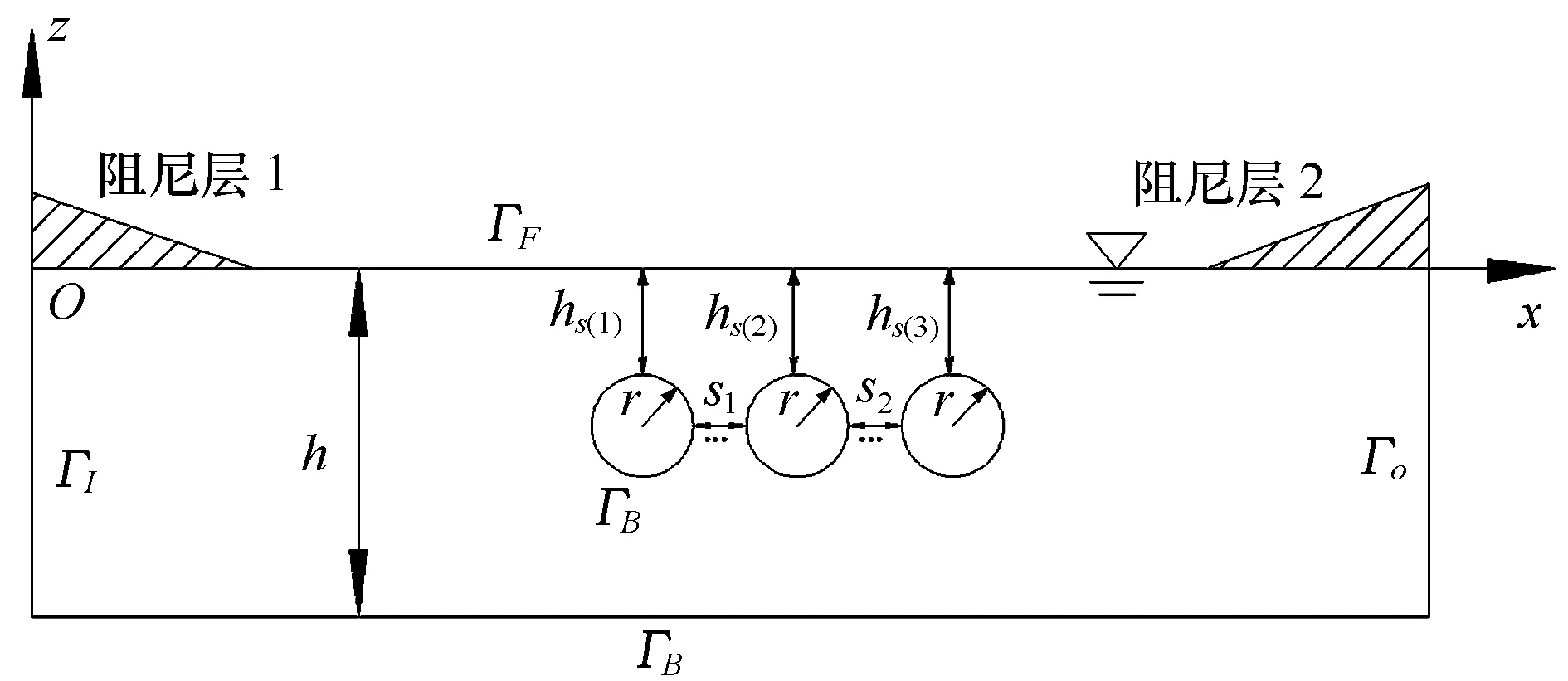
图1 二维数值水槽示意图Fig.1 Sketch of a 2D numerical wave flume

在瞬时自由水面ΓF上，满足完全非线性运动学和动力学边界条件，采用混合欧拉-拉格朗日方法更新自由水面，并在计算域上游和下游区域的自由水面分别布置人工阻尼层吸收从结构反射回来的波浪和出流波浪。进而自由表面运动学和动力学边界条件可写为如下形式：

在ΓF上,

(2)

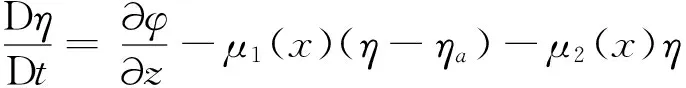
(3)

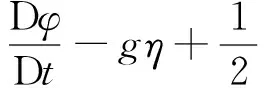
在ΓF上,

(4)

式中，g表示重力加速度；η表示自由水面的铅垂位移；ηa和φa仅在阻尼区域1中采用，表示在没有结构物且计算条件相同时的波面高度和速度势参考值，本文采用二阶Stokes解析解代替。阻尼项μ1(x)和μ2(x)表示成如下形式：

(5)

式中，Lb为阻尼层宽度,取为1.5倍波长；x1(2)分别为左、右阻尼层起始位置。

在水槽入射边界ΓI上，给定波浪速度传播的二阶Stokes解析解：

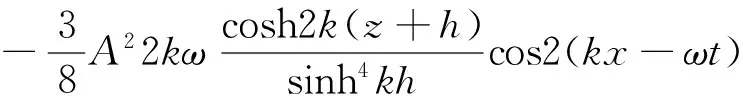
(6)

式中，A为入射波幅；k为波数；ω为角频率；ω和k满足色散方程。

在水槽底面Γd和物面ΓB上，满足固壁不可渗透边界条件，即

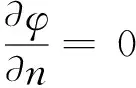
(7)

2.2 数值求解

在整个流域内对速度势应用格林第二定理，可得到如下边界积分方程：

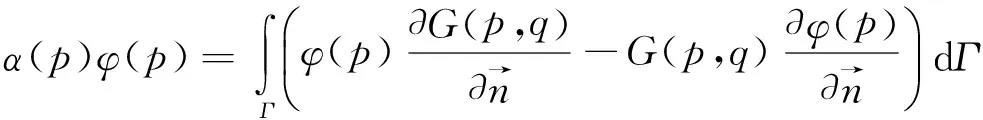
(8)

式中，p=(x0,z0)为源点；q=(x,z)为场点；α(p)为固角系数；Γ为流域边界，包括自由水面边界和固体边界；G为简单格林函数，考虑到水底镜像，可以表示为如下形式:

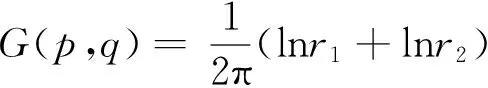
(9)

式中，

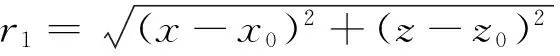
对整个计算域边界采用三节点的二次边界元进行离散，对每个单元进行数学变换，转换成等参坐标(ξ)下的等参单元，采用二次形状函数插值方法保证单元内几何量和物理量的连续分布。并通过求解离散为线性方程组的方程(8)分别得到自由水面和物面上的未知速度势方向导数和速度势。计算中认为当前时刻物面ΓN上的速度势法向导数和自由水面Γf上的速度势是已知的，根据积分方程计算当前时刻物面ΓN上的速度势和自由水面ΓF上的速度势法向导数，然后应用四阶Runga-Kutta法，根据自由水面条件式(2)计算下一时刻的水质点位置和自由水面ΓF上的速度势，再对自由水面重新划分网格，重新应用积分方程计算下一时刻物面上的速度势和自由水面上的速度势法向导数。这样计算周而复始，直到计算结束[11—12]。

通过上述求解就可以计算得到计算域内各个位置处的波面时间历程，进而通过利用潜体系统下游两点波面时间历程，采用两点法[3, 9]进行分离得到高阶自由波和锁相波的幅值，下文中将重点对高阶自由波特性进行分析。

3 试验模型

模型试验在大连理工大学海岸和近海工程国家重点实验室的波流水槽中进行，水槽长69 m，宽2.0 m，如图2a所示，在水槽一端配备有推板式单向造波机，水槽末端设置有消波缓坡装置。经测试，水槽实验段反射很小，表明水槽末端的消浪效果良好，反射对实验结果影响基本可以忽略。为了保证实验的二维效果，沿x轴方向将水槽被分割成宽度分别为1.2 m和0.8 m两部分，试验模型布置在0.8 m宽试验段。图2b和c给出了试验模型布置图，模型圆柱直径D=0.2 m，宽度与试验段同宽，第一个模型距离造波机约47 m，模型两侧由两片薄板支承，圆柱间间距可以调节，淹没水深也可以从0.2～0.4 m变化。试验水深统一设置为0.6 m，波浪周期T为0.95 s和1.1 s，入射波幅A=0.02 m和0.03 m，考虑双、三圆柱间距s1(2)分别为D、2D以及3D时，下游高阶谐波的变化情况。

图2 试验装置图Fig.2 The experimental setup

图3以双圆柱试验为例，给出了浪高仪布置情况，使用9根采集精度0.01 cm的浪高仪，其中浪高仪G1和G2位于圆柱上游约1倍波长位置处，G6、G7、G8和G9位于圆柱下游约1倍波长位置处，G6和G7以及G8和G9间距为0.1 m，G7和G8之间间距为0.2 m。浪高仪G3、G4、G5分别位于上游潜体正上方、潜体系统的中间位置以及下游潜体的正上方，而在三圆柱系统中G3、G4、G5则分别位于3个圆柱的正上方。

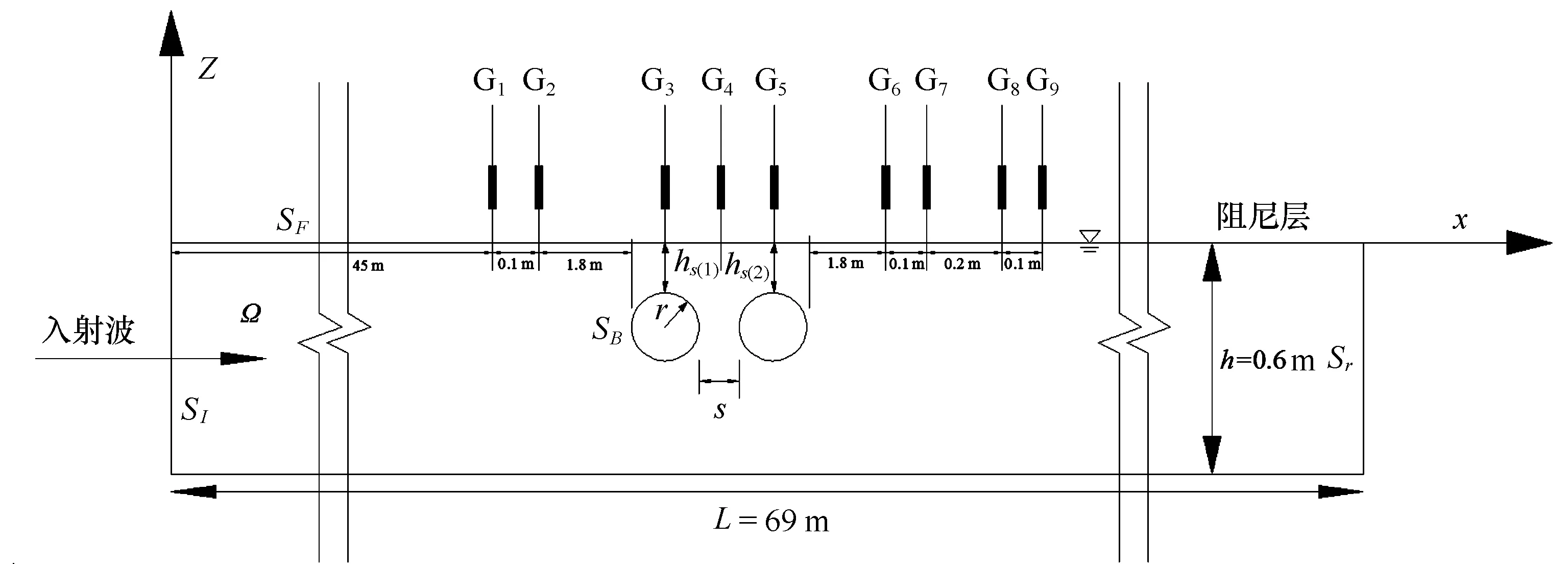
图3 试验装置布置示意图Fig.3 Schematic of the experimental setup

4 结果与分析

4.1 模型验证

作为算例，考虑淹没水深hs=0.2 m，间距s=D=0.2 m，周期T=1.1 s，波幅A=0.03 m时，对波浪分别与淹没双圆柱、三圆柱作用进行数值模拟来验证数模的收敛性和准确性。在数模中，计算域长度取14倍波长，水槽两端各设置1.5λ的阻尼层区，第一个潜体距离入射边界5倍波长，然后依次按间距s布置其他潜体。通过开展数值收敛性实验，自由水面上每个波长布置15个单元，计算域垂向边界布置12个单元，每个圆柱表面布置20个单元；时间步长△t=T/60，每个算例模拟40个周期。经对比30T和35T两个时刻的波面分布，发现两时刻波面吻合良好，验证了数值模型稳定性。

图4给出了双圆柱系统和三圆柱系统情况下G2、G4、G5和G6四点波面时间历程，及数值结果与试验数据对比情况。由图4可以看出，数值结果和实验数据吻合很好，说明本文所建立数值模型对波浪与多圆柱结构相互作用问题能很好地模拟。

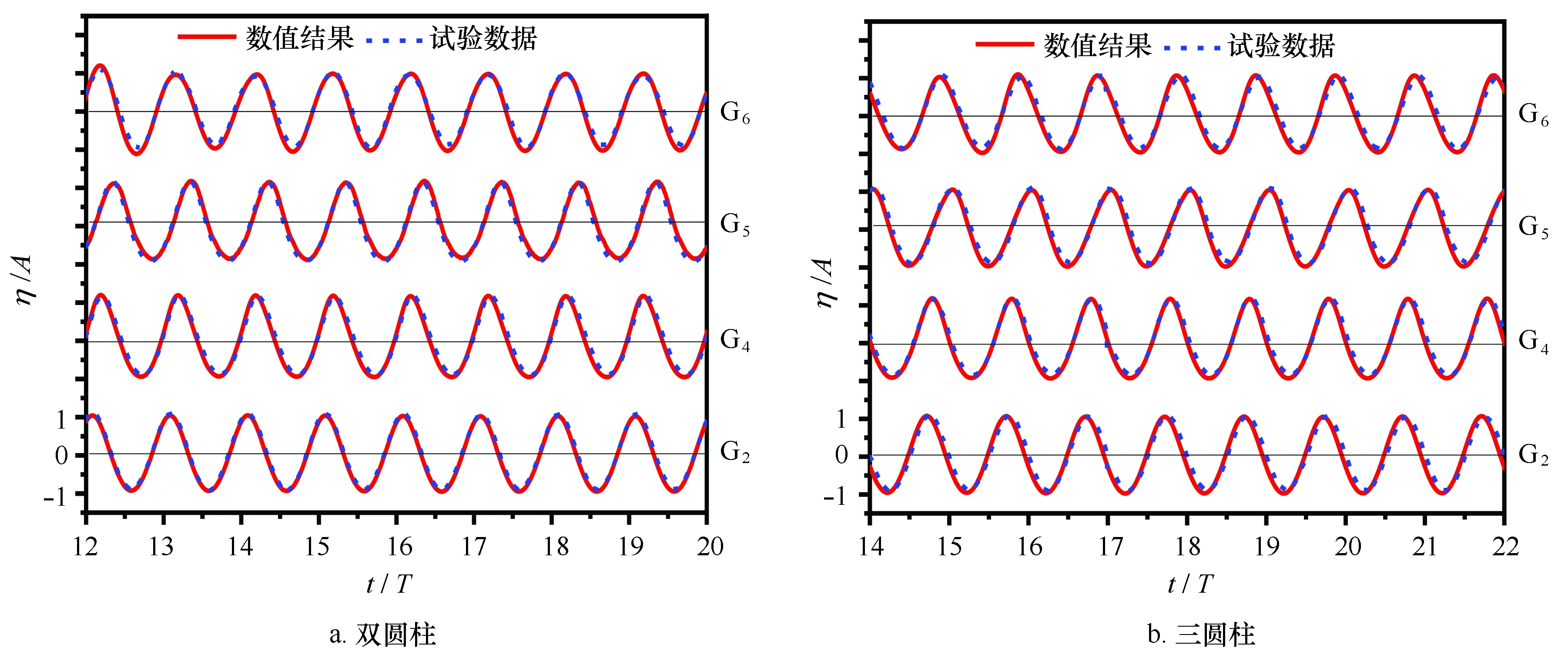
图4 双、三圆柱系统不同位置波面时间历程(s1(2)=D, hs= 0.2 m, T=1.1 s, A=0.03 m)Fig.4 Time series of the surface elevations at various positions for the cases of dual and three submerged cylinder(s1(2)=D, hs=0.2 m,T=1.1 s, A=0.03 m)

图5给出了双、三圆柱下游基频和二阶自由波幅值随圆柱间距变化的试验和数值计算结果对比。三圆柱间距s1=s2，横坐标为无量纲化的圆柱间距s/D。可以看出，高阶谐波随双、三圆柱系统间距的变化呈现较为相似，基频波幅值随双圆柱间距增大逐渐减小但并不明显，而二阶自由波幅值则随双圆柱间距呈现起伏变化的趋势。数模基频波幅值要略大于试验结果，这是因为基于势流理论数值模型未能考虑流体黏性所引起的能量耗散。流体黏性效应和流动分离主要影响波浪的透射过程[13—14]，导致了预测的透射系数要稍偏大，但仍能较好地预测二阶自由波幅值，表明透射过程中能量耗散主要发生在基频波中，而对高阶谐波影响相对较小。因此，本文数值模型能够较为准确地对波浪与双、三圆柱作用诱发的高阶自由谐波问题进行模拟。

图5 T=1.1 s时双、三圆柱下游高阶谐波幅值随圆柱间距变化Fig.5 Variations of the first and second-harmonic free wave amplitudes downstream dual/triple cylinders against the interval s/D

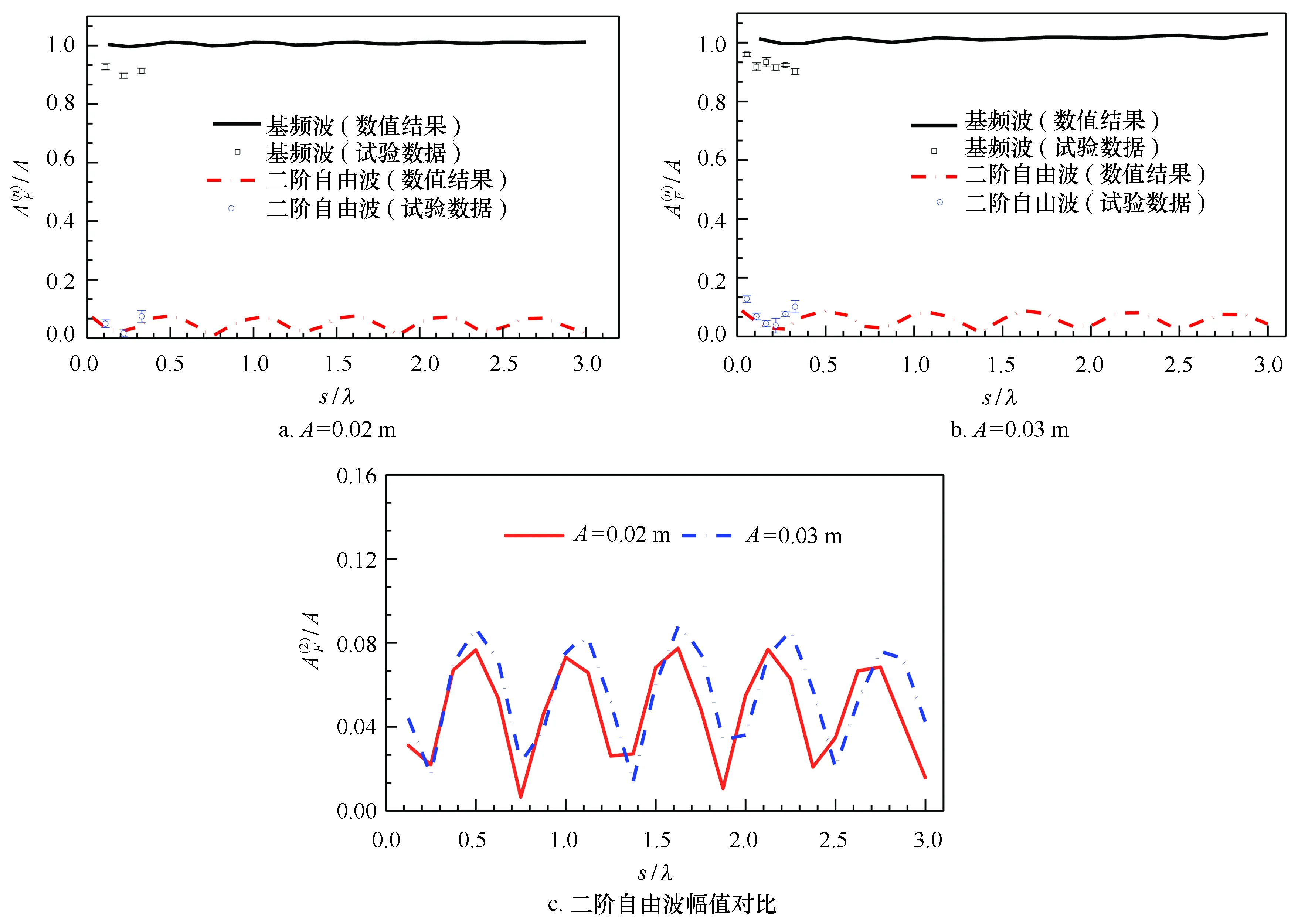
图6 基频和二阶自由波幅值随双圆柱系统间距的变化(D=0.2 m, T=1.1 s)Fig.6 Variations of the first and second free harmonic wave amplitudes with the gap distance between the two cylinders with D=0.2 m and T = 1.1 s

图7 各阶自由谐波幅值随三圆柱系统间距的变化(s1=s2，T=1.1 s)Fig.7 Variations of the various harmonic free wave amplitudes with the interval of the three cylinders system

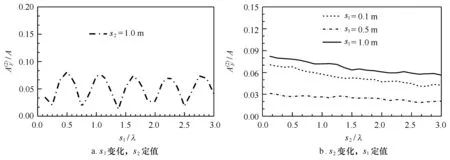
图8 二阶自由波幅值随三圆柱系统间距的变化(T=1.1 s)Fig.8 Variations of the second harmonic free wave amplitudes with the interval of the three cylinders system

4.2 多潜体下游的高阶谐波特性

接下来通过开展更多的数值试验，分析不同情况下潜体间距对高阶自由谐波幅值的影响。图6给出了波幅A=0.02 m和0.03 m情况下，双潜体系统下游产生的基频和二阶自由波波幅随间距s的变化情况。其中，淹没双圆柱的直径均为D=0.2 m，横坐标s通过除以波长λ进行无量纲化。由于本文试验水槽的长度条件所限，试验中s/λ被限定在0.33以内。从图中可以看出，二阶自由波幅值随无量纲化双圆柱系统间距s/λ呈现周期性振荡变化的特点，这与图5中二阶自由波幅值起伏变化相一致，而且振荡重现距离约为0.5λ。图6c给出了入射波幅值A=0.02 m和0.03 m两种工况下，双圆柱系统下游二阶自由波幅值随间距变化关系的比较，可以看出其随入射波幅值的增大而增大，但振荡重现距离基本保持不变。

图7给出了3个淹没水平圆柱的间距相同时(即s1=s2)，结构下游各阶自由谐波幅值随间距s1(2)/λ的变化情况，并给出了与本文物理模型试验结果的对比情况。本文通过数值模拟发现，当3圆柱之间的间距s1与s2保持相同时，结构下游也出现了类似于双圆柱系统间距变化时的高阶谐波幅值振荡变化的特性，其振荡的重现距离同样约为0.5λ。

令下游两个圆柱间距s2固定为1.0 m，图8a给出了三潜体系统下游二阶谐波幅值随上游两个圆柱间距s1的变化情况，经过与3个圆柱的相互作用，二阶自由波幅值发生了周期性振荡的现象。在这种工况下，相当于在本文中双圆柱系统间距变化工况下下游再加入一个淹没圆柱，按上述双圆柱的高阶谐波特性，波浪在经过了前面两个圆柱作用后出现了随前两个圆柱间距变化振荡的高阶谐波，再经过第3个圆柱的作用依然表现为随前两个圆柱间距振荡。

相反地，令前两个圆柱间距s1分别固定为0.1 m, 0.5 m和1.0 m，图8b给出了后两个圆柱间距s2变化情况下，二阶自由谐波幅值随下游两圆柱间距s2变化情况。可以看出，在固定了上游两个圆柱的间距后，二阶自由谐波幅值并未随下游两圆柱间距的变化出现类似于图8a中的周期性振荡现象，而是随下游两个圆柱间距的增大而减小，二阶自由波幅值总体上随下游两圆柱间距s2的增大而减小。但是，通过对比还可以发现，当取同一个s2时，上游两圆柱间距分别取s1=0.1 m，0.5 m和1.0 m时的二阶自由波的幅值之间也表现为振荡变化的，这与上述高阶谐波会随潜体间距振荡变化的结论是一致的。

5 结论

本文基于势流理论和时域高阶边界元方法，建立了模拟波浪与双、三潜体作用的二维完全非线性数值波浪水槽模型。运用两点分离法得到潜体后的各个高阶谐波的波浪形态。通过与试验数据进行对比验证了本文模型的正确性。研究发现：双圆柱系统下游高阶自由谐波幅值随双潜体间距呈现周期性振荡变化的特点，振荡重现距离约为波长的一半，二阶自由波幅值随着入射波幅的增大而增大，但振荡重现距离不受影响。对于三潜体系统，下游高阶自由谐波幅值随着上游两圆柱间距呈周期性振荡变化关系，而随着下游两圆柱间距增大而呈单调递减关系。

[1] Patarapanich M. Maximum and zero reflection from submerged plate[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering,1984, 2: 171-181.

[2] Dick T M, Brebner A. Solid and permeable submerged breakwaters[C]//Proc. 11th Coastal Eng. Conf., London, 1968, 72, 1141-1158.

[3] Grue J. Nonlinear water waves at a submerged obstacle or bottom topography[J]. Journal of Fluid Mechanics, 1992, 244: 455-476.

[4] Brossard J, Perret G, Blonce L, et al. A Higher harmonics induced by a submerged horizontal plate and a submerged rectangular step in a wave flume[J]. Coastal Engineering, 2009, 56(1):11-22.

[5] Ohyama T, Nadaoka K. Transformation of nonlinear wave train passing over a submerged shelf without breaking[J].Coastal Engineering, 1994, 24 (1/2): 1-22.

[6] 郑永红, 沈永明, 吴修广, 等. 用改进的Boussinesq方程模拟潜堤上的波浪变形[J]. 中国工程科学, 2004, 6(4): 34-40.

Zheng Yonghong, Shen Yongming, Wu Xiuguang,et al. Simulation of wave propagation over a submerged bar using a modified boussinesq equation[J]. Engineering Science, 2004, 6(4): 34-40.

[7] 张洪生, 冯文静, 商辉. 非线性波传播的新型数值模拟模型及其试验验证——引入变换速度变量[J]. 海洋学报, 2007, 29(5): 161-173.

Zhang Hongsheng, Feng Wenjing, Shang Hui. A new approach to numerical simulation of nonlinear wave propagation and its experimental verification[J]. Haiyang Xuebao, 2007, 29(5):161-173.

[8] Luth H R, Klopman G, Kitou N. Kinematics of waves breaking partially on an offshore bar; LDV measurements of waves with and without a net onshore current[R]. Report H-1573, Delft Hydraulics, 1994: 40.

[9] 陈丽芬, 宁德志, 滕斌, 等. 潜堤后高阶自由谐波的研究[J]. 海洋学报, 2011, 33(6): 165-172.

Chen Lifen, Ning Dezhi, Teng Bin, et al. Study on the higher free harmonic waves on the lee side of a submerged bar[J]. Haiyang Xuebao, 2011, 33(6): 165-172.

[10] Ning Dezhi, Lin Hongxing, Teng Bin, et al. Higher harmonics induced by waves propagating over a submerged obstacle in the presence of uniform current[J]. China Ocean Engineering, 2014, 28(6):725-738.

[11] 陈丽芬, 宁德志, 滕斌, 等. 潜堤上波流传播的完全非线性数值模拟[J]. 力学学报，2011, 43(5):834-843.

Chen Lifen, Ning Dezhi, Teng Bin, et al. Fully nonlinear numerical simulation for wave-current propagation over a submerged bar[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(5): 834-843.

[12] 周斌珍, 宁德志, 滕斌. 造波板运动造波实时模拟[J]. 水动力学研究与进展, 2009, 24(4): 1-12.

Zhou Binzhen, Ning Dezhi, Teng Bin. Real-time simulation of waves generated by a wave maker[J]. Chinese Journal of Hydrodynamics, 2009, 24(4):1-12.

[13] Ting F C K, Kim Y K. Vortex generation in water waves propagating over a submerged obstacle[J]. Coastal Engineering, 1994, 24 (1/2): 23-49.

[14] Liu C R, Huang Z H, Keat Tan S. Nonlinear scattering of non-breaking waves by a submerged horizontal plate: Experiments and simulations[J]. Ocean Engineering, 2009, 36: 1332-1345.

Numerical and experimental investigations on higher harmonics induced by multiple horizontal cylinders

Li Qingxin1，Ning Dezhi1，Teng Bin1

(1.StateKeyLaboratoryofCoastalandOffshoreEngineering,DalianUniversityofTechnology,Dalian116024,China)

Based on potential flow theory, a numerical wave flume was founded to model the interaction of nonlinear waves and dual or triple submerged horizontal cylinders by using a time-domain higher-order boundary element method. The mixed Eulerian-Lagrangian technique was used for the refresh of free surface, and the 4th-order Runga-Kutta scheme was adopted for the time advance. The two-point method was adopted to separate the higher free harmonics from the downstream waves. Then the effects of interval of submerged objects and distribution scheme on the higher free harmonics were investigated. Meanwhile, physical tests were carried out for higher harmonics induced by multiple submerged objects in a wave flume. Good agreements between the numerical results and experimental data were obtained. It was found that higher free harmonic amplitude oscillates periodically with the variation of the interval in the dual cylinder system. And the reoccurrence interval is near to half wave length. In the triple cylinder system, higher free harmonics amplitude oscillates periodically with the first interval but decreases with the second interval.

nonlinear numerical wave flume；multiple submerged objects; higher harmonics; physical tests; higher boundary element method

10.3969/j.issn.0253-4193.2017.01.010

2016-04-27；

2016-07-01。

国家自然科学基金项目(51679036，51490672)；教育部新世纪优秀人才支持计划(NCET-13-0076)。

李庆昕(1991—)，男，甘肃省白银市人，主要从事波浪与潜体相互作用研究。E-mail:li_qing_xin@qq.com

*通信作者：宁德志，教授，从事海洋水动力研究。E-mail:dzning@dlut.edu.cn

P731.22

A

0253-4193(2017)01-0096-08

李庆昕，宁德志，滕斌. 多个淹没水平圆柱诱发高阶谐波特性的数值与试验研究[J]. 海洋学报, 2017, 39(1): 96-103,

Li Qingxin，Ning Dezhi，Teng Bin. Numerical and experimental investigations on higher harmonics induced by multiple horizontal cylinders[J]. Haiyang Xuebao, 2017, 39(1): 96-103, doi:10.3969/j.issn.0253-4193.2017.01.010