基于时间序列GA-SVR的水产品价格预测模型及验证
2017-01-17段青玲魏芳芳肖晓琰
段青玲,张 磊,魏芳芳,肖晓琰,王 亮
(中国农业大学信息与电气工程学院,北京 100083)
基于时间序列GA-SVR的水产品价格预测模型及验证
段青玲,张 磊,魏芳芳,肖晓琰,王 亮
(中国农业大学信息与电气工程学院,北京 100083)
水产品价格的准确预测有助于合理规划水产养殖,正确引导水产行业的发展。根据水产品价格序列的非线性、非平稳和周期性特点,提出了一种基于时间序列遗传优化(genetic algorithm,GA)支持向量回归(support vector regression,SVR)的水产品价格预测模型。该模型首先通过时间序列分析方法对价格序列进行平稳性检验和确定相关阶数,得到训练数据集;再利用遗传算法对支持向量回归模型的参数组合进行寻优,使用优化后的参数建立支持向量回归模型,然后使用模型进行预测。分别选取桂鱼、基围虾、梭子蟹的价格数据对模型进行验证,选取 2011-2014年的数据作为训练集,对2015年价格进行预测,结果表明:桂鱼、基围虾、梭子蟹的平均绝对误差分别为6.70%、7.82%、14.76%,均方根误差分别为5.853 1、23.701 1、13.858 0,且优于基于时间序列的SVR模型及BPANN模型的预测结果,可以为水产品价格的预测提供依据。
养殖;模型;支持向量机;价格预测;水产品;遗传算法;时间序列
0 引 言
中国是水产养殖大国,水产品价格的波动对水产行业的发展有着重要影响[1]。但是由于水产养殖的无序性,以及保鲜和运输的影响,导致水产品价格波动过大,有时会出现优质优量但不优价的情况。对水产品价格进行预测,能够使水产养殖者及时了解市场的变化趋势,合理规划养殖结构,做到有的放矢,使养殖利益最大化。同时,价格预测为政府制定相关行业政策提供科学依据,力求资源得到充分利用,促进水产行业健康可持续发展。
价格预测是依据市场经济规律,运用科学的方法,对未来价格的变动趋势所进行的分析和判断[2]。价格预测的主要模型有时间序列模型[3-5],回归分析模型[6-7],以及组合模型[8-10]。时间序列模型主要分析价格序列和时间之间的关系,根据历史数据的规律和特点对未来价格进行预测,这类模型对于线性预测效果较好,但对于非线性处理并不理想;回归分析模型是选择和预测对象关联较高的影响因子建立预测模型,价格的波动是由于影响因子的变化导致的,所以这种方法易于理解,但是对于影响因子的选择和数据的搜集较为困难;随着智能计算的发展,组合模型逐渐成为研究的热点,它的好处是可以结合各自的特点建立预测模型。Zhang等[11]构建了水产品价格预测支持系统,集成了神经网络、案例推理、移动平均、线性回归等模型,首先使用时间序列的方法对数据序列进行分析,然后根据数据序列的特点选用适当的模型进行预测。Li等[12]采用小波神经网络对水产品价格进行预测,并使用鲈鱼价格验证了模型的可行性。任海军等[13]给出了一种基于时间序列的AR_SVR模型的农产品价格预测方法,将时间序列和支持向量回归相结合,并在黄瓜价格上得到了验证。李哲敏等[14]将混沌理论和神经网络时间序列应用到农产品价格预测中,设计了动态混沌神经网络时间序列预测模型,以马铃薯时间序列价格为例进行了试验,优于传统的时间序列预测模型效果。还有一些学者应用不同的分析模型对预测的问题做了很多研究[15-21]。这些模型分别针对数据项的确定,核函数的选择,模型参数的优化给出分析方法,侧重于某一方面问题的解决。相较于一般的农产品,水产品价格具有价格弹性大的特点,由于养殖的特殊性,受产量、天气及交通运输等因素的影响,使得水产品价格序列具有非线性、非平稳、周期性的特点。但针对水产品价格预测的深入研究并不多,预测精度仍有待提高。
水产品价格是水产养殖业的关键指标,是消费者和养殖户都关心的问题。随着人们生活水平的不断提高,对水产品的营养价值也有了更科学的认识,水产品的消费日益增多。根据水产品价格的非线性、非平稳、周期性特点,本文给出基于时间序列遗传优化支持向量回归(geneticalgorithm-supportvector regression,GA-SVR)的水产品价格预测模型,对序列的平稳性、相关项阶数的确定、核函数的选择及参数的优化给出解决方法,以提高预测的精度。本文的主要工作在两方面:1)将时间序列的分析方法,遗传优化算法和支持向量回归模型结合起来,给出水产品价格的组合预测模型;2)使用组合模型对水产品价格数据做预测,通过和其他预测模型进行比较,验证模型的准确性。
1 模型原理
根据水产品价格的非线性、非平稳、周期性特点,本文给出了基于时间序列GA-SVR的水产品价格预测模型。首先对原始数据序列进行预处理,使得数据的波动映射到一个较小的区间上,然后使用时间序列的分析方法使得序列平稳化并确定相关项的阶数,生成训练数据集。SVR模型选取径向基核函数,通过GA算法的全局搜索能力对其参数进行寻优,建立预测模型。使用模型进行预测,得到预测值。
1.1 时间序列分析
水产品价格序列呈现出周期性和非平稳的特点,阶数的选择对预测结果的准确性会产生很大影响,可以通过偏自相关系数来确定序列的平稳性并确定相关阶数[22-23]。采用时间序列中偏自相关系数分析方法对价格序列进行分析,使得价格序列满足预测的基本要求,保证了预测的有效性,使得预测的结果更为真实。详细计算过程为:对于平稳的随机过程,其期望为常数,用来表示,即

式中E(·)为期望函数,x表示价格值,t表示对应的序数。平稳随机过程的方差σ也是一个常量:
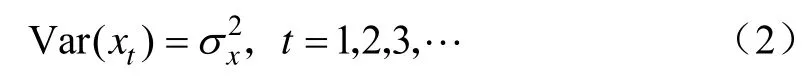
式中Var(·)为方差函数,x表示价格值,t表示对应的序数。方差σ用来度量随机过程取值对其均值μ的离散程度。设随机变量相隔的期数为h,则相隔h期的2个随机变量 xt与 xt+h的协方差即为滞后h期的自协方差,定义为:
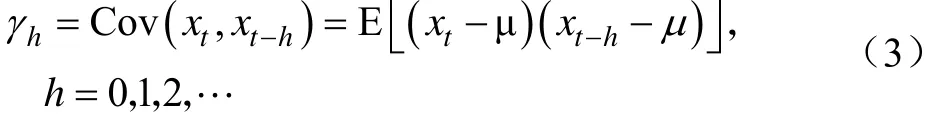
式中Cov(·)为自协方差函数,μ为得到的期望值,h表示相隔的期数。
自相关系数定义为:
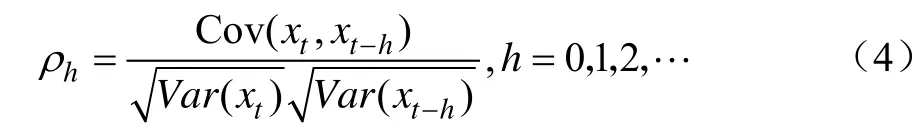
式中Cov(·)为自协方差函数,Var(·)为方差函数。因为对于一个平稳过程有:
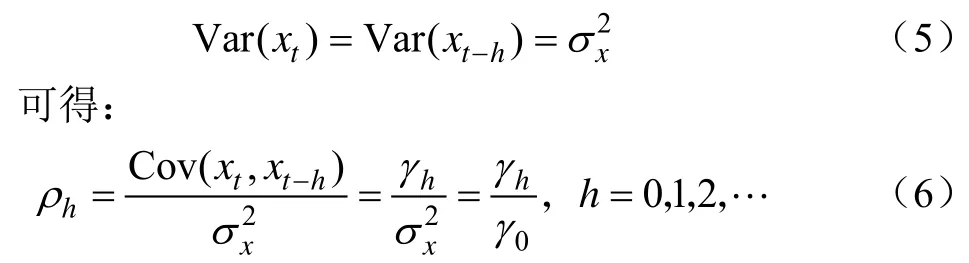
当h=0时,ρ0=1。以滞后期h为变量的自相关系数数列称为自相关函数。
偏相关系数的递推公式为:
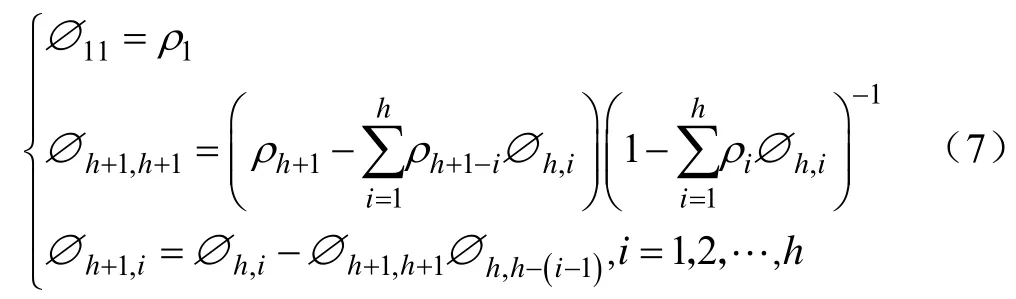
得到序列的偏相关系数∅h,h。统计推断的依据为平稳序列的自相关系数ρh和偏相关系数∅h,h均服从的正态分布,可以通过差分和季节差分操作使序列平稳化。假设存在正整数mar和mma,满足:
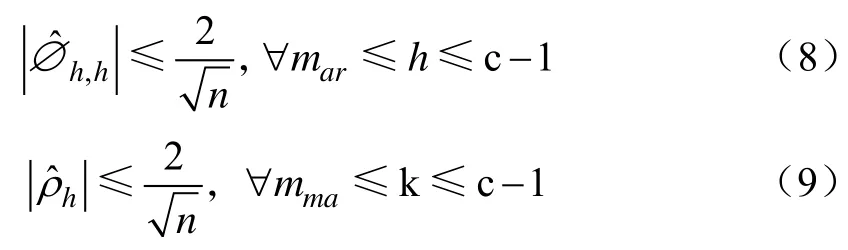
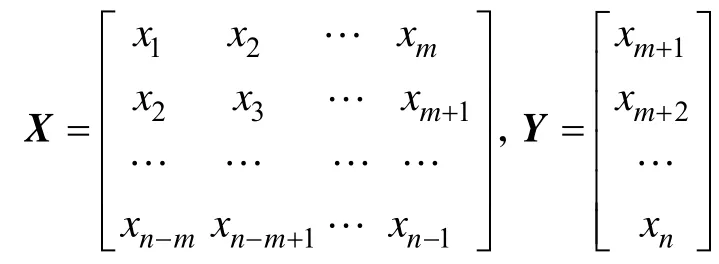
式中n和m均表示正整数,训练数据集包括训练子集X和期望值子集Y,x表示训练子集X和期望值子集Y中的元素。
1.2 SVR模型
对于水产品价格序列的非线性的特点,使用支持向量回归机可以很好的处理这个问题。使用得到的数据集来对序列进行拟合,生成预测模型。基于ε-SVR的时间序列预测问题的数学描述如下[24-26]。

式中∅(·)为模型算子,w和b为函数系数。其优化问题为:

式中C为惩罚因子,ε为不敏感损失参数。
考虑到价格序列非线性的特点,本文采用径向基函数作为SVR的核函数,那么,其决策函数就是:
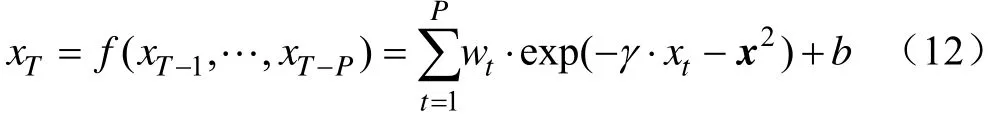
式中γ核函数系数,P为滞后阶数,w和b为预测函数系数。由此,即可得到预测输出,预测过程可描述为图1所示。
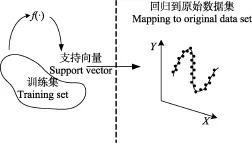
图1 支持向量回归SVR模型原理Fig.1 SVR model theory
1.3 GA优化算法
遗传算法(genetic algorithms,GA)是模拟自然界遗传机制和生物进化论而成的一种随机搜索算法,具有高效、并行、全局搜索等优点,不依赖于具体的问题领域,能够在搜索的过程中依据优胜劣汰的原则,随机进行信息交换,自动获取并积累搜索空间的知识,求得最优解。它把生物进化原理引入优化参数形成的编码串联群体中,按照所选择的适应度函数,通过遗传中的选择、交叉和变异对个体进行迭代,直至满足终止条件[27-29]。在这个过程中引入交叉验证(cross validation,CV)的机制,以减少数据集划分差异对算法的影响。交叉验证[30]是用来验证模型性能的一种统计方法,K折交叉验证是把训练集随机分成K个不相关的子集,然后用其中的K-1个子集作为训练子集,建立预测模型,其他的子集为验证子集。通过K次循环,使每个子集都充当一次验证子集,然后对这K次的均方误差(mean square error,MSE)取均值,作为K折交叉验证的均方误差。
对于采用径向基核函数的SVR,参数变量有3个,分别是核函数系数γ、惩罚因子C和损失参数ε。算法步骤如下:
1)染色体表示
染色体表示是指染色体的编码方式,常用的有二进制法,实数法等。这里采用实数编码,即每个染色体为一个实数串,对于待优化的参数γ,C,ε,染色体可以表示为,其中分别对应
2)适应度函数
适应度函数是衡量染色体优劣的指标。根据个体得到的参数,用训练数据对SVR进行训练,并预测其输出,把预测输出和期望输出之间的误差绝对值之和作为个体的适应度值。引入K折交叉验证机制后,适应度函数将K次均方误差的均值作为适应度值,计算公式如下:
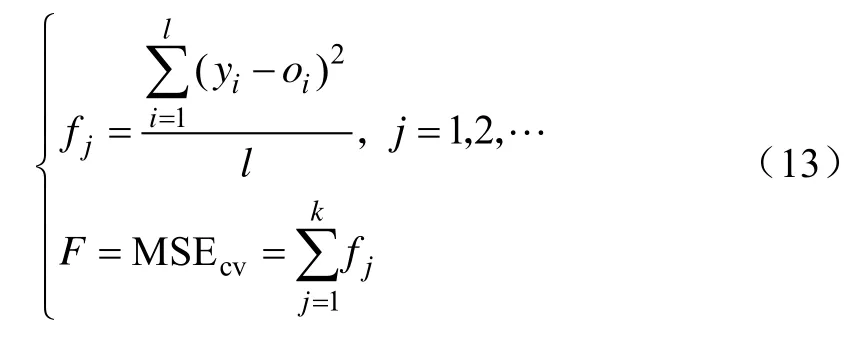
式中fj为K折交叉验证过程中一次循环产生的值,yi为真实值,oi预测输出;F为染色体的适应度值,值越小表示染色体越优,被选择的概率就越大。
3)选择操作
选择操作用于模拟自然界优胜略汰的自然选择过程。为了确保进化过程朝着优化的方向进行,选择过程根据求得的适应度值的大小,淘汰一些较差的个体,选出一些比较优良的个体。选择算子有轮盘赌法、锦标赛法等,本文选择轮盘赌法,即适应度值越优的染色体被选择的概率越大。
4)交叉操作
交叉操作相当于的是生物遗传基因的重组,本质是为了增强算法的全局搜索能力。所谓交叉是把两个染色体的部分结构加以替换重组而生成新个体的操作。若一对染色体被确定进行交叉操作,则需要确定一个或多个交叉点。由于染色体采用实数编码,所以本文选择的交叉算子是单点实数交叉法,即不同染色体在对应的某个位置上以概率 Pcross进行交叉操作,Pcross一般取值在[0.4,0.99]之间。
5)变异操作
变异操作的本质是增强算法的局部搜索能力,避免陷入局部极小值,同时维持种群的多样性,以防止过早收敛。因此,变异的概率 Pmut应取较小的值,通常在[0.0001,0.1]区间内选择。
当迭代达到最大次数,就停止迭代,输出最优参数组合。算法流程如图2所示。
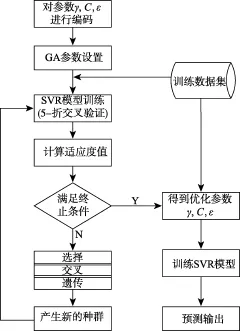
图2 GA-SVR模型流程Fig.2 GA-SVR model process
2 试验及分析
2.1 数据获取
本文中的试验数据来自中国农业信息网北京新发地批发市场水产品价格(从2011年1月到2015年12月),水产品的常见品种有鱼、虾、蟹等类别,品种的选取参考了水产品的分类,考虑到当地饮食习惯,以及市场销售情况,文章分别从各个类别中选取了居民日常食用较为广泛的桂鱼、基围虾和梭子蟹作为试验对象,共抓取桂鱼1541条记录,基围虾1525条记录,梭子蟹1430条记录,如图3所示。通过解析得到价格数据值,然后计算每个月有记录天数对应的月均值。将 2 011年到 2 014年数据训练模型,并预测2015年的值,和2015年的真实数据比较,验证模型的准确性。
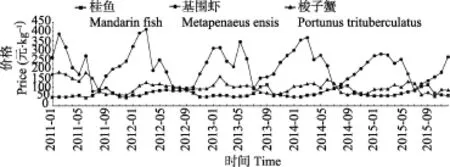
图3 水产品月平均价格Fig.3 Aquaculture product monthly average price
2.2 预测过程
由于数据序列的取值范围及波动情况不同,应首先对原始数据序列进行预处理,如归一化、取对数等操作。针对水产品价格波动区间较大的特点,这里选择取对数操作,将价格序列映射到一个较小的区间上,之后的操作应用于取对数后的序列上。
首先,对数据序列进行平稳化处理,进行季节差分或一阶差分,通过自相关系数判断序列的平稳性。经过处理后,检验序列的偏相关系数,确定序列的相关阶数,可得相关阶数分别为:以此可生成训练数据集。
然后,使用遗传算法对训练集的参数进行优化。初始化遗传算法设置,设种群规模为20,进化代数为200,参数γ,C,ε的搜索范围分别为[0,100],[0,100],[0.01,1],迭代的过程采用5-折交叉验证机制。当迭代达到最大次数后,输出最优组合。
通过遗传算法计算,得到优化后的参数组合如表1所示。以此来建立模型,并预测2015年的值。预测结果如图4所示。
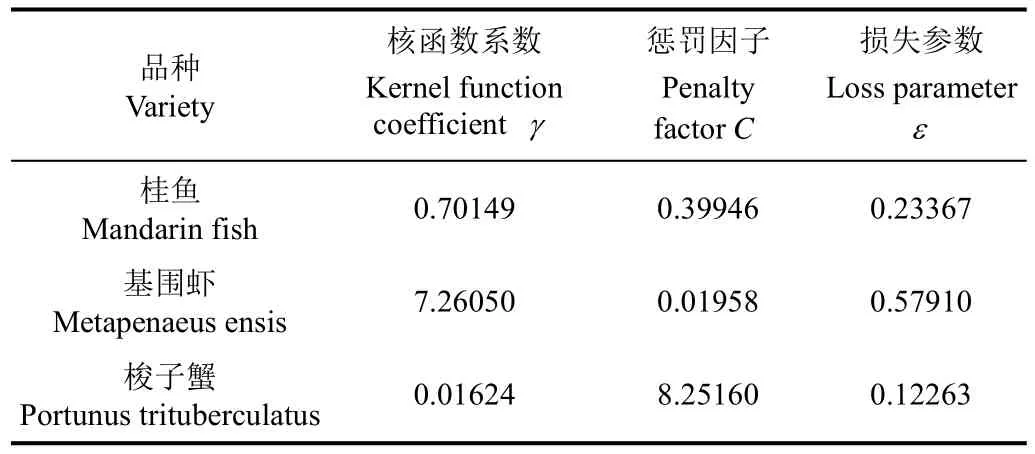
表1 参数组合Table 1 Parameter combination
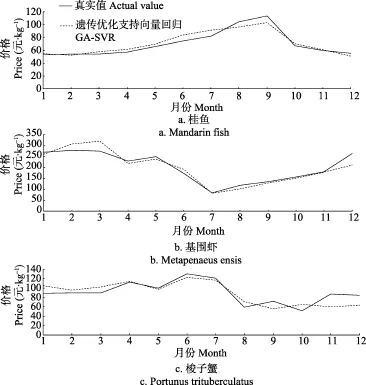
图4 预测值和真实值的比较Fig.4 Comparison between forecasted values with actual values
2.3 对比分析
本文选取了相对误差(relative error,RE),平均绝对误差百分比(mean absolute percentage error,MAPE),均方根误差(root mean square error,RMSE)来评估模型的准确性,计算公式如下:
式中 yi为真实值,yi'为预测值,n为数据项个数。评价指标的误差值越小,模型的准确性越好,详细指标如表2所示。
本文同时使用了基于时间序列的SVR模型和BPANN对价格序列进行了预测,预测结果如图5所示。由表3可知不同模型对于2015年的预测性能,桂鱼的预测结果相较于SVR模型,MAPE和RMSE分别降低了14.32%和36.76%,相较于BPANN模型,MAPE和RMSE分别降低了16.98%和11.71%;基围虾的预测结果相较于SVR模型,MAPE和RMSE分别降低了32.64%和21.55%,相较于BPANN模型,MAPE和RMSE分别降低了46.91%和31.1%;梭子蟹的预测结果相较于SVR模型,MAPE和RMSE分别降低了7.51%和12.64%,相较于BPANN模型,MAPE和RMSE分别降低了11.13%和29.5%;由分析可知,本文提出的模型具有较好的预测性能。
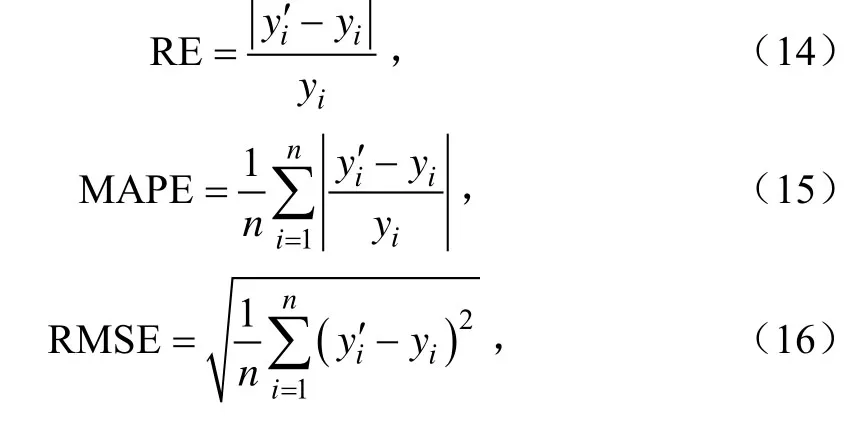
由实地调得知,水产品的供应受季节,天气,交通运输等因素的影响很大,价格的波动随着这些因素的变化呈现出不规则的波动。以梭子蟹为例,梭子蟹是一种海蟹,主要养殖在辽宁、山东、福建、广东等东部沿海地区,由于北京地处北方,该市场的梭子蟹主要由渤海湾等地供应,每年的5月和8月是梭子蟹上市时期,受供求关系影响,价格波动较大,在5月是上市期,价格小幅回落,但由于供应量并不是很大,加上 6 月进入休渔期,造成之后的一段时间价格涨幅较大,8月前后,随着梭子蟹的大规模上市,价格大幅回落。对比预测结果,和实际规律相符。
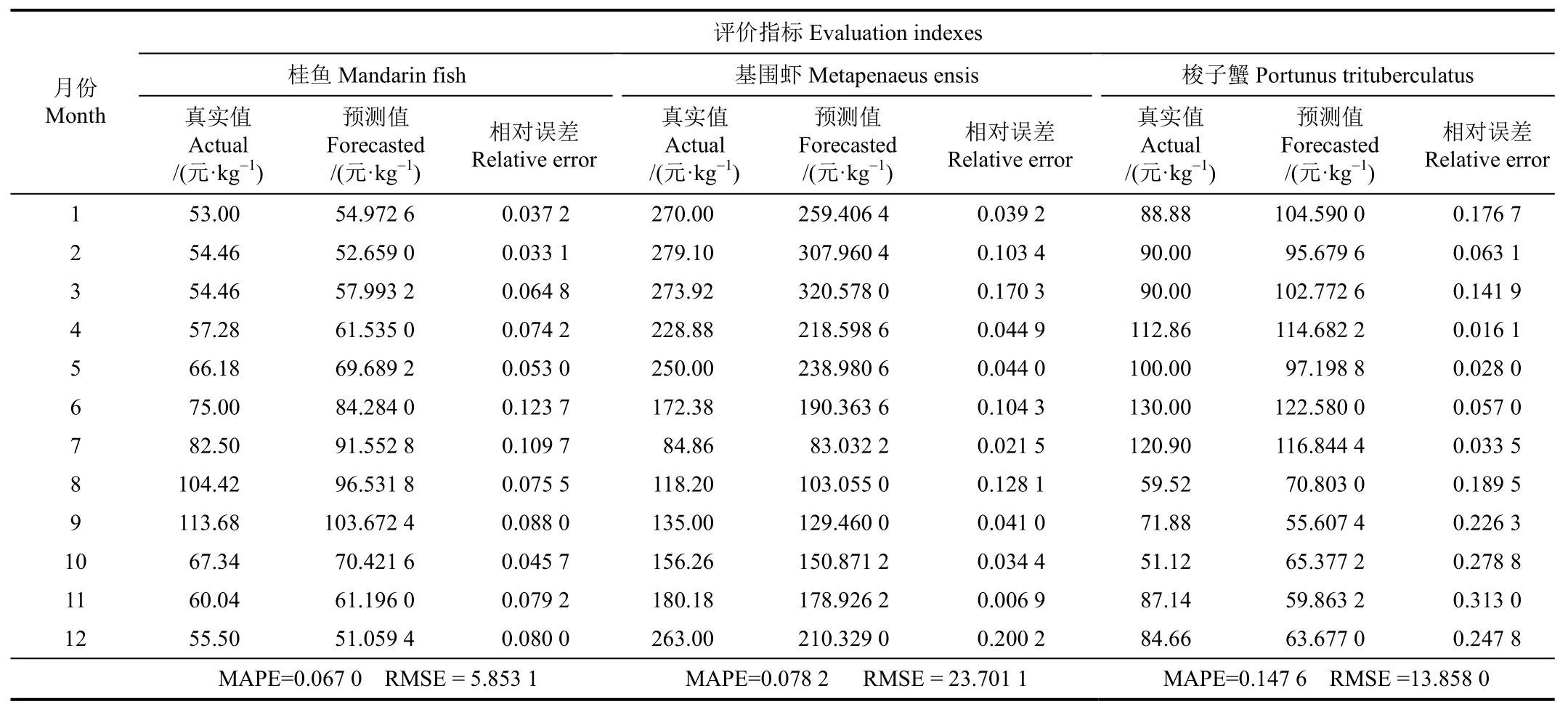
表2 价格预测值和真实值对比Table 2 Comparison between forecasted values with actual values of price

图5 基于时间序列的BPANN、SVR、GA-SVR模型的预测对比Fig.5 Comparison of forecasted values of BPANN,SVR,GA-SVR based on time series
价格的波动往往受多种因素的影响,受养殖品种、养殖地区、市场状况、交通运输、饮食习惯等因素的影响,很难以某一地区某一品种价格的影响因素来推断其他品种,加上数据搜集难度较大,这是水产品价格预测的难点。本文从技术角度对水产品价格的研究进行分析,结合相关领域的研究成果,以求找到一种适应性强的方法来对价格进行预测。而且随着大数据时代的来临,数据将会越来越丰富、完整,本文模型将会得到进一步的验证。
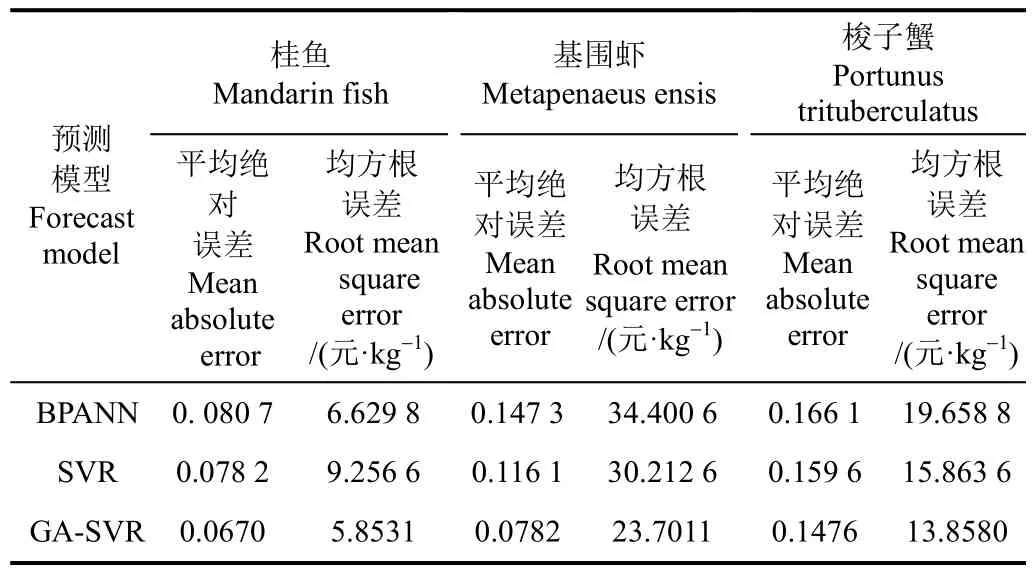
表3 不同模型价格预测结果Table 3 Forecasted values of BPANN,SVR,GA-SVR based on time series for price
3 结 论
本文根据水产品价格序列的非线性、非平稳和周期性特点,提出了一种基于时间序列分析GA-SVR水产品价格预测模型,研究主要结论如下:
1)通过时间序列的分析方法,计算水产品价格的偏自相关系数,通过差分以及季节差分操作,可以将水产品价格序列平稳化,并确定相关阶数项,构建满足预测条件的训练数据集。
2)针对水产品价格的非线性、周期性等特点,选择SVR作为预测模型,采用径向基核函数,通过GA优化算法对模型的参数进行优化,给出一种组合GA-SVR模型用于水产品价格的预测。
3)使用桂鱼、基围虾、梭子蟹的价格数据对模型进行验证,对2015年价格数据进行预测,预测结果同真实值相比较,桂鱼、基围虾、梭子蟹的平均绝对误差分别为0.0670、0.0782、0.1476,均方根误差分别为5.8531、23.7011、13.8580。同时使用了基于时间序列的SVR模型和BPANN模型进行对比,本文提出的模型预测精度更优。可知,该模型可以为水产品价格的预测提供参考依据。
[1] 王威巍,梁鸽峰,孙珅. 中国水产品市场价格波动特征研究[J]. 中国渔业经济,2015,33(6):56-63. Wang Weiwei,Liang Gefeng,Sun Chen.The price fluctuant characteristics research on China’s aquatic products market[J]. Chinese Fisheries Economics,2015,33(6):56-63.(in Chinese with English abstract)
[2] 任宏伟. 农产品市场价格预测方法探析[J]. 中国农学通报2011,27(26):209-212. Ren Hongwei. Study on methods of forecasting the farm products prices[J]. Chinese Agricultural Science Bulletin,2011,27(26):209-212.(in Chinese with English abstract)
[3] Tarjei K. A time series spot price forecast model for the Nord Pool market[J]. Electrical Power and Energy Systems,2014,61:20-26.
[4] Rojas I,Valenzuela O,Rojas F,et al. Soft-computing techniques and ARMA model for time series prediction[J]. Neur Computing,2008,71:519-537.
[5] Daniel B,Carlo M. Forecasting copper prices with dynamic averaging and selection models[J]. North American Journal of Economics and Finance,2015,33:1-38
[6] Deepak S,Swarup K S. Electricity price forecasting using artificial neural networks[J]. Electrical Power and Energy Systems,2011,33:550-555.
[7] Li Ganqiong,Xu Shiwei,Li Zhemin,et al. Using quantile regression approach to analyze price movements of agricultural products in china [J]. Journal of Integrative Agriculture,2012,11(4):674-683.
[8] Xiong Tao,Li Chongguang,BaoYukun,et al. A combination method for interval forecasting of agricultural commodity futures prices[J]. Knowledge-Based Systems,2015,77:92-102.
[9] 周世昊,林苍祥,倪衍森. 基于遗传算法和神经网络的新股上市价格预测法[J]. 计算机工程,2007,33(22):9-11. Zhou Shihao,Lin W T,Ni Yansen. Price forecasting approach for initial public offerings using genetic algorithm and neural network[J]. Computer Engineering,2007,33(22):9-11.(in Chinese with English abstract)
[10] Zhu Bangzhu,Wei Yiming. Carbon price forecasting with a novel hybrid ARIMA and least squares support vector machines methodology[J]. Omega,2013,41:517-524.
[11] Zhang Xiaoshuan,Hu Tao,Brain Revell,et al. A forecasting support system for aquatic products price in China[J]. Expert Systems with Application,2005,28:119-126.
[12] Li Hongwei,Gao Xiaoxiang,Cheng Kejun. The application of wavelet neural network in prediction of the fish price[J]. Applied Mechanics and Materials,2014,687-691:1945-1949.
[13] 任海军,孙瑞志,刘广利. 基于AR_SVR模型的时间序列预测算法的研究[J]. 计算机工程与设计,2010,31(2):421-424. Ren Haijun,Sun Ruizhi,LiuGuangli. Research of time-series forecasting algorithm based on AR_SVR model[J]. Computer Engineering and Design,2010,31(2):421-424.(in Chinese with English abstract)
[14] 李哲敏,许世卫,崔利国,等. 基于动态混沌神经网络的预测研究:以马铃薯时间序列价格为例[J]. 系统工程理论与实践,2015,35(8):2083-2091. Li Zhemin,Xu Shiwei,Cui Liguo,et al. Prediction study based on dynamic chaotic neural network:taking potato timeseries prices as an example[J]. Systems Engineering-Theory &Practice,2015,35(8):2083-2091.(in Chinese with English abstract)
[15] Peng K L,Wu C H,Goo Y J. The development of a new statistical technique for relating financial information to stock market returns[J]. International Journal of Management,2004,21(4):492-505.
[16] Byeonghwa P,Jae K B. Using machine learning algorithms for housing price prediction:The case of Fairfax County,Virginia housing data [J]. Expert Systems with Applications,2015,42:2928-2943.
[17] 孙建明. 基于能繁母猪存栏量和猪粮价比的猪肉价格预报[J]. 农业工程学报,2013,29(13):1-6. Sun Jianming. Pork price forecast based on breeding sow stocks and hog-grain price ratio[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE),2013,29(13):1-6.(in Chinese with English abstract)
[18] 屠星月,薛佳妮,郭承坤,等. 基于时间序列与RBF的农产品市场价格短期预测模型[J]. 广东农业科学,2014(23):168-173. Tu Xingyue,Xue Jiani,Guo Chengkun,et al. Short-term forecast of agricultural products price based on time series and RBF[J]. Journal of Guangdong Agricultural Sciences,2014(23):168-173.(in Chinese with English abstract)
[19] Jiajun Zong,Quanyin Zhu. Apply grey prediction in the agriculture production price[C]//International Conference on Multimedia Information Networking and Security,2012.
[20] Longqin Xu,Shuangyin Liu. Study of short-term water quality prediction model based on wavelet neural network[J]. Mathematical and Computer Modelling,2013,(58):807-813.
[21] 李宏伟,高小翔,程可军. 基于小波神经网络的鱼类价格预测研究[J]. 中国渔业经济,2014,32(4):61-66. Li Hongwei,Gao Xiaoxiang,Cheng Junke. Research on price forecasting of fish based on wavelet neural network method[J]. Chinese Fisheries Economics,2014,32(4):61-66.(in Chinese with English abstract)
[22] Jonathan DC,KungS C. Time Series Analysis with Applications in R(Second Edition)[M]. New Yourk:Springer-Verlag,2008.
[23] Pai P F,Lin C S. A hybrid ARIMA and support vector machines model in stock price forecasting [J]. The International Journal of Management Science,2005,33(6),497-505.
[24] 刘广利. 基于支持向量机的经济预警方法研究[D]. 北京:中国农业大学,2003. Liu Guangli. Research on Economic Early Warning Methods Based on Support Vector Machine[D]. Beijing:China Agricultural University,2003.(in Chinese with English abstract)
[25] 王快妮,钟萍,赵耀红. 鲁棒SVR在金融时间序列预测中的应用[J]. 计算机工程,2011,37(15):155-163. Wang Kuaini,Zhong Ping,Zhao Yaohong. Application of robust support vector regression in financial time sequence prediction[J]. Computer Engineering,2011,37(15):155-163.(in Chinese with English abstract)
[26] 张豪,罗亦泳,张立亭,等. 基于遗传算法最小二乘支持向量机的耕地变化预测[J]. 农业工程学报,2009,25(7):226-231. Zhang Hao,Luo Yiyong,Zhang Liting,et al. Cultivated land change forecast based on genetic algorithm and least squaressupport vector machines[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE),2009,25(7):226-231.(in Chinese with English abstract)
[27] Jiawei H,Micheline K,Jian P. Data mining:concepts and techniques[M]. Third edition Burlington:Morgan Kaufmann Publishers,2012.
[28] 王海军,柳敏燕,高娟. 利用遗传算法和支持向量机测算农用地理论单产和可实现单产[J]. 农业工程学报,2013,29(19):244-252. Wang Haijun,Liu Minyan,Gao Juan. Calculation of theoretical and accessible yields of agricultural land based on geneticalgorithm and support vector machine[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE),2013,29(19):244-252.(in Chinese with English abstract)
[29] 王海军,柳敏燕,高娟. 利用遗传算法和支持向量机测算农用地理论单产和可实现单产[J]. 农业工程学报,2013,29(19):244-252. Wang Haijun,Liu Minyan,Gao Juan. Calculation of theoretical and accessible yields of agricultural land based on genetic algorithm and support vector machine[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE),2013,29(19):244-252.(in Chinese with English abstract)
[30] Wang Jue,Qiao Jianzhong. Parameter selection of SVR based on improved k-fold cross validation[J]. Applied Mechanics and Materials,2014,462:182-186.
Forecasting model and validation for aquatic product price based on time series GA-SVR
Duan Qingling,Zhang Lei,Wei Fangfang,Xiao Xiaoyan,Wang Liang
(College of Information and Electrical Engineering,China Agricultural University,Beijing 100083,China)
Fluctuations in aquatic product prices have an important impact on the development of the aquaculture industry. Accurate forecasting results can enable farmers to keep abreast of changes in the market and rationally plan aquaculture. Based on the non-linear,non-stationary and periodicity of the aquatic product price series,a genetic algorithm(GA) support vector regression(SVR) model based on time series for forecasting aquatic product price was presented in this paper. Firstly,the time series method was applied to the price series,the autocorrelation function was used to judge the stability,and the partial correlation coefficient was used to judge the data items,then the training data set was obtained. After that,the genetic algorithm was used to optimize the parameters of support vector regression. The parameters of SVR based on radial basis kernel function were kernel function coefficient,penalty factor,and loss parameter. We designed these three parameters by using real number coding individual representation. We used the selection operation to select the mean square error as the fitness function,to calculate the fitness value of each individual,and to select the individuals with better fitness value. By use of the crossover operation,we selected the point intersecting as crossover operator with different individuals,respectively in a corresponding position to a certain probability. The nature of mutation operation was used to enhance the local search algorithm,and avoid falling into the local minimum. We mutated individual to a certain probability and change its current value,then generated new population. We introduced the mechanism of 5-fold cross validation to the process of each iteration to obtain the optimized parameter combination. Finally,the support vector regression model was established by using the optimized parameters to forecast the price of aquatic products in the next period. In this paper,we selected mandarin fish,metapenaeus ensis and portunus trituberculatus as the experimental objects. The experimental data we used were the value of aquatic product price from January 2011 to December 2015 of Beijing Xinfadi market website(http://www.xinfadi.com.cn). After craw ling the web data-including 1,541 records of mandarin fish,1,525 records of metapenaeus ensis and 1,430 records of portunus trituberculatus,we calculated the monthly average price to represent the price of a period. We trained the proposed model by using data from 2011 to 2014,and forecasted the price of the next year. Through comparing with the real value,the mean absolute percent error of mandarin fish,metapenaeus ensis and portunus trituberculatus was 6.70%,7.82% and 14.76%,with corresponding root mean square error of 5.8531,23.7011 and 13.8580,respectively. After surveying the market,we found that the results of forecasting were more in line with the actual situation. In this paper,the SVR model and the BP neural network model based on time series were all used in contrast experiment of our model. The experiment results showed that our model was superior. According to the characteristics of aquatic product price in this paper,we proposed a combined model for the determination of the relevant items of the aquatic product price series,the selection of the kernel function and the parameter optimization. The results showed that the proposed model can provide the basis for the forecasting of aquatic product price.
aquaculture;models;support vector machine;price forecast;aquatic product;genetic algorithm;time series
10.11975/j.issn.1002-6819.2017.01.042
F304.2;TP301.6
A
1002-6819(2017)-01-0308-07
段青玲,张 磊,魏芳芳,肖晓琰,王 亮. 基于时间序列GA-SVR的水产品价格预测模型及验证[J]. 农业工程学报,2017,33(1):308-314.
10.11975/j.issn.1002-6819.2017.01.042 http://www.tcsae.org
Duan Qingling,Zhang Lei,Wei Fangfang,Xiao Xiaoyan,Wang Liang. Forecasting model and validation for aquatic product price based on time series GA-SVR[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE),2017,33(1):308-314.(in Chinese with English abstract)doi:10.11975/j.issn.1002-6819.2017.01.042 http://www.tcsae.org
2016-05-16
2016-10-24
公益性行业(农业)科研专项(201203017);宁波市农业重大(重点)择优委托科技攻关项目(2011C11006)
段青玲,女,教授,博士生导师,主要从事农业智能信息处理与数据挖掘研究。北京 中国农业大学信息与电气工程学院,100083。Email:dqling@cau.edu.cn
