耦合非线性波动方程爆破时间的下确界

刘玉龙

(山西大学 数学科学学院,山西 太原 030006)

耦合非线性波动方程爆破时间的下确界

刘玉龙

(山西大学 数学科学学院,山西 太原 030006)

考虑带有阻尼和源项的非线性耦合波动方程,为了获得波动方程爆破时间的下确界，在有限时间爆破的结果下,选择适当辅助函数G(t),利用Cauchy不等式和能量初值E(0)的估计得到有关G(t)和G′(t)的微分不等式,并最终通过对时间积分进而得到非线性耦合波动方程爆破时间的下确界．

耦合;非线性波动方程;爆破;下确界

0 引 言

近年来,对于波动方程解的爆破问题有很多研究,其中关于非线性耦合波动方程解的存在和爆破问题已有许多结果[1-11]．然而,对于波动方程爆破时间的研究还不是很多．爆破的准确时间一般很难确定,因此在实践中计算出爆破时间的上、下确界具有重要意义．在关于波动方程爆破问题的文章中,一般从结果中都可以得到爆破时间的上确界,而下确界的确定却还没有被普遍关注．文献[12]研究了耦合波动方程,在适当假设情况下证明了解的爆破,并且得到了爆破时间的上确界．文献[13]研究了两类非线性波动方程爆破时间的问题,在解爆破的前提下精确地计算出了爆破时间的下确界.文献[14]利用辅助函数在爆破的前提下得到了爆破时间的下确界．

本文考虑如下的问题

(1)

其中Ω是R2中的有界区域,且具有光滑边界∂Ω,m,γ≥1,T>0;文章将在解爆破的前提下得到问题(1)爆破时间的下确界．

为了获得问题(1)解的爆破结果,作如下假设.

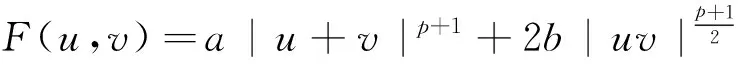
(A2) 存在正常数c0,c1使得∀(u,v)∈R2，F(u,v)满足

c0(|u|p+1+|v|p+1)≤F(u,v)≤c1(|u|p+1+|v|p+1).

(2)

(A3) 给定函数ρ1,ρ2对所有s>0满足

(3)

文章中记‖·‖p为Lp(Ω)的范数,用E(t)表示系统(1)的能量．

1 相关定理及引理

首先给出解的局部存在性定理和解的爆破结果．

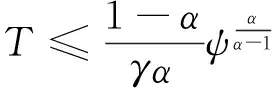
为了获得系统(1)爆破时间的下确界,有以下引理．

引理1[14]假设Ω是Rn(n=2,3)中的有界区域,且具有光滑边界∂Ω．如果u(x)在Ω上满足u(x)∈C1而且在∂Ω上u(x)=0,则有不等式

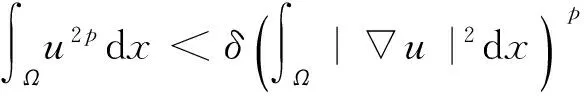
2 主要结果及证明

定理3 假设u(t)是系统(1)的解,且u(t)在有限时间T爆破,则

其中

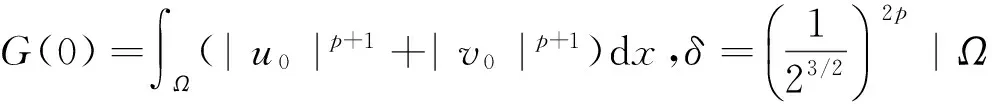
证明 首先,对系统(1)的前两个等式两边分别同乘ut与vt，并且在Ω上积分，得

∫Ω(uttut+utut+|ut|m-1utut)dx=∫Ω(div(ρ1(|u|2)u)ut+f1(u,v)ut)dx,

(4)

∫Ω(vttvt+vtvt+|vt|γ-1vtvt)dx=∫Ω(div(ρ1(|v|2)v)vt+f2(u,v)vt)dx.

(5)

则式(4)等号右边第一项可化简为

∫Ω(div(ρ1(|u|2)u)utdx= ∫∂Ωρ1(|u|2)u·ν·utdΓ-∫Ωρ1(|u|2)uutdx=

-∫Ωρ1(|u|2)uutdx.

∫Ωρ1(|u|2)uu|2)dx.

同理,

∫Ωρ2(|u|2)uu|2)dx.

所以,式(4)～(5)可化简为

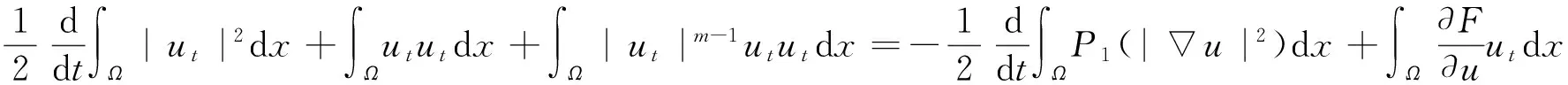
(6)

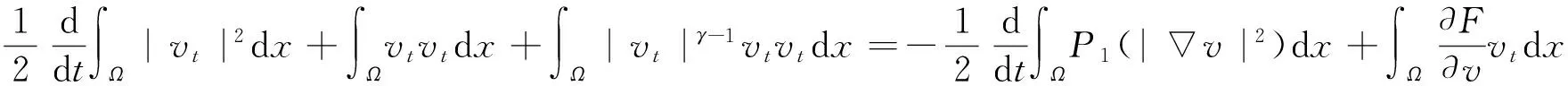
(7)

将式(6)与式(7)相加,整理可得

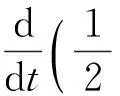
-∫Ωututdx-∫Ω|ut|m-1ututdx-∫Ωvtvtdx-∫Ω|vt|γ-1vtvtdx.

所以可以得到能量及其导数的表达式,即

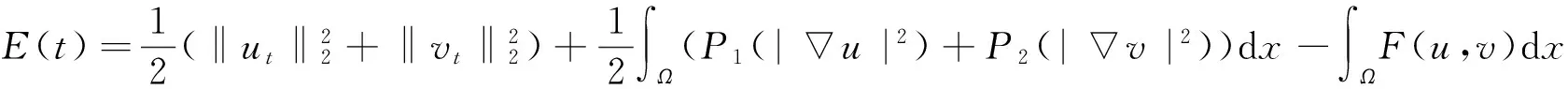
(8)

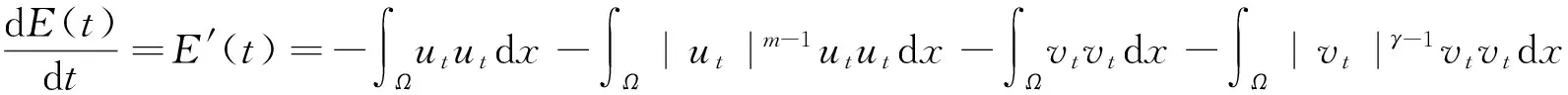
(9)

由式(9)得

则

E(t)≤E(0).

(10)

所以由式(8)和式(10)可得

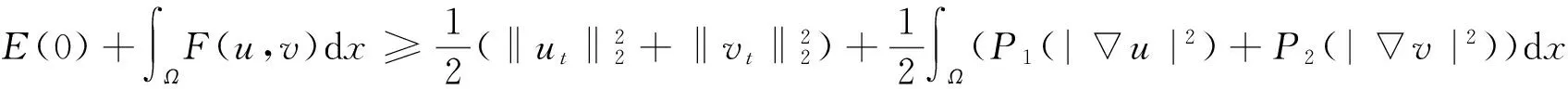
(11)

接下来设辅助函数为

G(t)=∫Ω(|u|p+1+|v|p+1)dx,

则关于t求导可得

G′(t)=(p+1)∫Ω(|u|put+|v|pvt)dx.

利用Cauchy不等式得

由式(11)可得

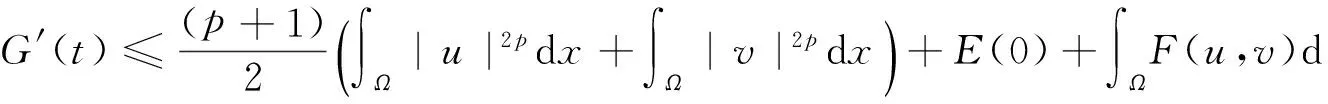
再利用引理1可得

(12)

由式(3)可知,存在一个常数c2使得

成立，即

c2Pi(s)≥s,

所以有

c2P1(|u|2)≥|u|2,c2P2(|v|2)≥|v|2.

(13)

将式(13)代入式(12)可得

再由式(11)可得

根据式(2)可以得到

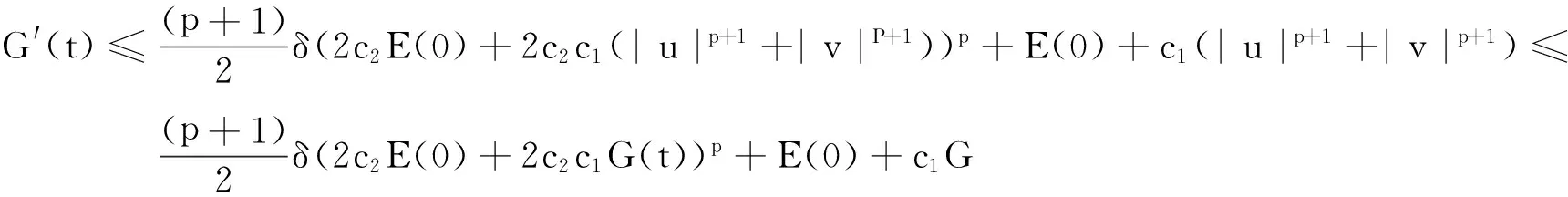
(14)

证毕．

3 结束语

计算波动方程解爆破时间的下确界的关键是G(t)的选取以及得到最终的微分不等式.而且G(t)一定要是非线性的,否则会与前面的爆破结果相矛盾,而利用引理中的方法就可保证G(t)非线性．本文尽可能使得爆破时间的下确界更精确,但由于技术和方法的局限,求解爆破时间的更为精确的方法还有待进一步研究．

[1] GLASSEY R T.Blow-up theorems for nonlinear wave equations[J].Math Zeit,1973,132(3):183-203.

[2] PITTS D R,RAMMAHA M A. Global existence and non-existence theorems for nonlinear wave equations[J].Indiana Univ Math J,2002,51(6):1479-1509.

[3] LEVINE H A,TODOROVA G.Blow up of solutions of the Cauchy problem for a wave equation with nonlinear damping and source terms and positive initial energy[J].Proc Amer Math Soc,2001,129(3):793-805.

[4] TODOROVA G,VITILLARO E.Blow-up for nonlinear dissipative wave equations in Rn[J].J Math Anal Appl,2005,303(1):242-257.

[5] SONG H T,XUE D H.Blow up in a nonlinear viscoelastic wave equation with strong damping[J].Nonlinear Anal,2014,109:245-251.

[6] ZHOU J.Global existence and blow-up of solutions for a Kirchhoff type plate equation with damping[J].Appl Math Computation,2015,265(c):807-818.

[7] MESSAOUDI S A.Blow up and global existence in a nonlinear viscoelastic wave equation[J].Math Nachr,2003,260(1):58-66.

[8] MESSAOUDI S A.Blow up of positive-initial-energy solutions of a nonlinear viscoelastic hyperbolic equation[J].J Math Anal Appl,2006,320(2):902-915.

[9] MESSAOUDI S A.Blow up in a nonlinearly damped wave equation[J].Math Nachr,2001,231(1):1-7.

[10] LIU W J.General decay and blow-up of solution for a quasilinear viscoelastic problem with nonlinear source[J].Nonlinear Anal,2010,73:1890-1904.

[11] BALL J.Remarks on blow up and nonexistence theorems for nonlinear evolutions equations[J].Quart J Math Oxford,1977,28(4):473-486.

[12] WU J,LI S.Blow-up for coupled nonlinear wave equations with damping and source[J].Appl Math Lett,2011,24(7):1093-1098.

[13] ZHOU J.Lower bounds for blow-up time of two nonlinear wave equation[J].Appl Math Lett,2015,45:64-68.

[14] PHILIPPIN G A.Lower bounds for blow-up time in a class of nonlinear wave equation[J].Z Angew Math Phys,2015,66(1):129-134.

[15] GEORGIEV V,TODOROVA G.Existence of the wave equation with nonlinear damping and source term[J].J Differential Equations,1994,109(2):295-308.

[16] CAVALCANTI M M,DOMINTI V N,FERRERIA J.Existence and uniform decay for nonlinear viscoelastic equation with strong damping[J].Math Methods Appl Sci,2001,24:1043-1053.

编辑、校对：师 琅

Lower bounds for blow-up time of the coupled nonlinear wave equations

LIUYulong

(School of Mathematical Sciences,Shanxi University,Taiyuan 030006,China)

Considering the coupled nonlinear wave equation, to obtain the lower bounds for wave equations,in case of blow-up result,selecting suitable auxiliary functionG(t) and get the differential inequality onG(t) andG′(t) by Cauchy inequality and the estimation of the initial energyE(0).Finally,by integrating over the time, the lower bounds of blow-up time for coupled nonlinear wave equation is obtained.

coupled;nonlinear wave equation;blow-up;lower bounds

1006-8341(2016)04-0450-05

10.13338/j.issn.1006-8341.2016.04.006

2016-04-27

国家自然科学基金资助项目(11171195)

刘玉龙(1990—),男，山西省临汾市人，山西大学博士研究生,研究方向为分布参数系统控制理论.

E-mail:liuylmath@139.com

刘玉龙.耦合非线性波动方程爆破时间的下确界[J].纺织高校基础科学学报,2016,29(4)：450-454.

LIU Yulong.Lower bounds for blow-up time of the coupled nonlinear wave equations[J].Basic Sciences Journal of Textile Universities,2016,29(4):450-454.

O 175.29

A