Ti-Ni金属间化合物电子结构与力学性质的第一性原理计算

王 鹏，李 军，林崇智，杨 柳，彭 琳，王 莹，肖 聪，陈敬超



Ti-Ni金属间化合物电子结构与力学性质的第一性原理计算

王 鹏1，李 军1，林崇智1，杨 柳1，彭 琳1，王 莹1，肖 聪1，陈敬超2

(1. 攀钢集团研究院有限公司钒钛资源综合利用国家重点实验室，攀枝花 617000；2. 昆明理工大学稀贵及有色金属先进材料教育部重点实验室，昆明 650093)

采用基于密度泛函理论(DFT)的第一性原理赝势平面波方法，计算Ti-Ni合金系中TiNi、Ti2Ni和TiNi3金属间化合物的平衡晶格常数、生成焓、内聚能、力学性质、德拜温度和电子结构。计算结果表明：TiNi、Ti2Ni和TiNi3金属间化合物均具有热力学稳定性且容易合金化生成，合金形成能力由强到弱的排序为TiNi3、TiNi、Ti2Ni；3种金属间化合物的晶体结构在能量上和力学上都是稳定的，结构稳定性由大到小排序依次为Ti2Ni、TiNi、TiNi3；TiNi和Ti2Ni为延性相(延展性Ti2Ni大于TiNi的)，TiNi3的延展性较差；3d电子是TiNi、Ti2Ni和TiNi3金属间化合物的最主要的成键电子，在这3种金属间化合物中，随着Ni相对含量的增加，平均成键电子数增多，共价键的比例增加，化学键的强度增强，金属性减弱，从而使得其弹性模量、硬度和德拜温度均逐渐升高。

Ti-Ni；金属间化合物；电子结构；力学性质；第一性原理

钛钢复合板结合了钛(合金)的耐腐蚀性与钢的强度和塑性，同时降低了原材料的成本，因而其在化工、核能、海洋工程等领域有着广泛的应用[1−3]。然而，当前钛钢复合板的生产过程中仍面临着界面结合性能差的问题。钛和钢直接复合会在扩散区域形成多种脆性金属间化合物(如TiC、Fe2Ti/FeTi等)[4−6]，同时不同物相热膨胀系数的失配会导致界面过渡区域残余应力的产生。为了缓解上述问题，可以添加适当的中间层材料。中间层材料的加入，一方面可以降低钛和钢的复合温度、减少热膨胀系数的失配，另一方面可以降低或阻止脆性金属间化合物的形成[7]。因优异的高温抗腐蚀性能和在铁中具有较高的固溶度，金属镍(Ni)成为了较为理想的中间层候选材料，并且得到了研究者的广泛关注[8−16]。

以镍作为钛钢复合板的中间层，铁−镍过渡区域形成的是Fe-Ni无限固溶体，没有中间相的生成，因而镍−铁界面具有良好的结合性能。在钛−镍界面，依据Ti-Ni二元平衡相图，过渡区可能会有Ti-Ni金属间化合物的生成。文献[13−17]均证实在以镍作为中间层的钛钢复合板的界面过渡区中，存在TiNi、Ti2Ni和TiNi3这3种金属间化合物，未发现其它类型的Ti-Ni金属间化合物。另外，在Ti和Ni两种金属(合金)扩散连接的界面区域中，也发现了这3种金属间化合物的存在[18−21]。

因此，弄清TiNi、Ti2Ni和TiNi3金属间化合物的结构与性质，对深入研究钛−镍界面特性以及提升钛−镍界面结合性能都具有积极的意义。然而，钛−镍界面过渡区域中TiNi、Ti2Ni 和TiNi3金属间化合物的单相性质(如弹性模量)的实验测量极为困难。据作者所知，当前没有文献对这3种金属间化合物的性质进行系统的理论或实验研究。为此，本文作者采用基于密度泛函理论的第一性原理计算方法对TiNi、Ti2Ni和TiNi3金属间化合物在基态下的稳定性、力学性质、德拜温度、电子结构等进行了理论计算。

1 晶体结构与计算方法

1.1 晶体结构

实验分析测试TiNi、Ti2Ni和TiNi3金属间化合物的晶体结构如图1所示。其中，TiNi为单斜晶体结构，空间群为121/1，共包含4个原子，Ti原子和Ni原子分别占据2e (0.2164, 0.25, 0.4176)和2e (0.6752, 0.25, 0.0372)位置；Ti2Ni为复杂面心立方晶体结构，空间群为3-，共包含96个原子，Ti原子占据16c (0.125, 0.125, 0.125)和48f (0.311, 0, 0)位置，Ni原子占据32e (0.912, 0.912, 0.912)位置；TiNi3密排六方晶体结构，空间群为63/，共包含16个原子，Ti原子占据2a (0, 0, 0)和2c (0.3333, 0.6667, 0.25)位置，Ni原子占据6g (0.5, 0, 0)和6h (0.833, 0.666, 0.25)位置。在本计算中，TiNi和TiNi3以图1所示的惯习晶胞作为计算模型，Ti2Ni以其原胞(包含24个原子)作为计算模型。

图1 Ti-Ni金属间化合物晶体结构(灰色代表Ni原子，蓝色代表Ti原子)

1.2 计算方法

计算采用基于密度泛函理论(DFT)的CASTEP (Cambridge serial total energy package)软件包[22]。在广义梯度近似(GGA)框架下，采用PW91[23]泛函形式确定交换关联函数。采用超软赝势(Ultrasoft)描述价电子与离子实之间的相互作用，平面波截断能为420 eV。布里渊区(Brillouin zone)积分采用Monkhorst-Park[24]方案进行网格划分，网格间隔为0.025/Å。自洽计算(SCF)应用Pulay混合密度法[25]，收敛精度为1.0×10−7eV/atom。采用BFGS (Broyden-Flecher-Goldfarb- Shanno) 算法[26]对晶胞进行几何全优化(包括晶胞参数和原子内坐标)，收敛条件为：体系能量小于1.0×10−6eV/atom，最大Hellmann-Feynman力低于0.005 eV/Å，原子最大偏移量小于1.0×10−4Å，体系最大应力小于0.007 GPa。

利用几何优化后的晶胞进行弹性常数的计算，计算方法为应力−应变法，每种应变模式下施加6个不同振幅的应力，最大振幅为0.2%。收敛条件为：体系能量小于1.0×10−6eV/atom，最大Hellmann-Feynman力低于0.002 eV/Å，原子最大偏移量小于1.0×10−4Å。本研究所有计算均考虑了自旋极化效应。

2 计算结果与讨论

经几何全优化，得到TiNi、Ti2Ni和TiNi3金属间化合物基态下的稳定构型，其晶格参数如表1所列。从表1可以看出，Ti2Ni和TiNi3晶格参数的理论计算值与实验值符合得非常好，而TiNi晶格参数的理论计算值与实验值之间出现了较大的偏差，但其体积偏差仅为1.15%。由于实验值为室温下的测试结果，而理论计算值为0 K下的计算结果，单斜晶体结构TiNi较大的各向异性可能是造成这一现象的原因。

2.1 生成焓与内聚能

为了研究Ti-Ni金属间化合物的合金形成能力和结构稳定性，分别计算了生成焓和内聚能。生成焓定义为原子从其单质生成化合物过程中所释放(或吸收)的能量，计算公式为

内聚能的定义为将晶体分解成单个原子所需消耗的能量，其计算公式为

(2)

式中：tot为所计算晶胞的总能；Ti和Ni分别为晶胞中Ti原子和Ni原子的原子个数；和分别为平衡态下Ti原子和Ni原子的平均能量；和分别为孤立Ti原子和Ni原子的能量；基于式(1)和(2)，计算得到TiNi、Ti2Ni和TiNi3的生成焓与内聚能列于表1。从表1可以看出，计算值与文献参考值之间存在一定的偏差，但这种偏差较小且3种金属间化合物生成焓值和内聚能值的相对大小关系与参考文献是一致的，因此计算结果仍是可靠的。

负的生成焓代表着一个热力学自发过程，生成焓越负则晶体的热力学稳定性越高，合金形成能力越强。由表1可以看出，生成焓由小到大排序为TiNi3、TiNi、Ti2Ni(＜0)，表明3种金属间化合物均具有热力学稳定性，容易合金化形成。其中，TiNi3金属间化合物的热力学稳定性最高，合金形成能力最强。

内聚能表示原子在其晶体状态与自由状态之间的能量变化。内聚能为负值预示着对应的晶体结构能够稳定存在，内聚能越负则晶体结构越稳定。计算结果表明，TiNi、Ti2Ni和TiNi3金属间化合物的内聚能均为负值，因而3种金属间化合物的晶体结构在能量上是稳定的。晶体结构稳定性由强到弱的排序为Ti2Ni、TiNi、TiNi3。

2.2 力学性质

2.2.1 弹性常数及力学稳定性

弹性常数反映了晶体抵抗弹性变形的能力，与晶体材料的许多性质都有着密切的联系。TiNi、Ti2Ni和TiNi3金属间化合物独立二阶弹性常数的计算结果如表2所列。

由于弹性应变能要求为正值，因而需要对稳定晶体结构的弹性常数作一些限定。根据BORN等[33]晶体力学稳定性条件—弹性常数矩阵的各阶顺序主子式均大于0，可以计算得到不同晶体结构的力学稳定性条件。单斜晶体、立方晶体和六方晶体的力学稳定性条件[34]如下：

单斜晶体的力学稳定性条件：

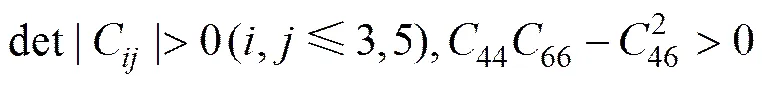
立方晶体的力学稳定性条件：

(4)

六方晶系的力学稳定性条件：

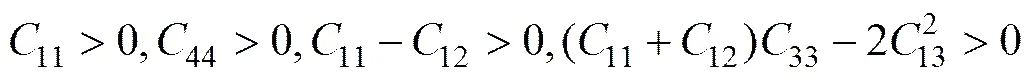
利用独立弹性常数(见表2)，计算表明3种金属间化合物均满足力学稳定性条件，这说明TiNi、Ti2Ni 和TiNi3金属间化合物的晶体结构在力学上是稳定的。

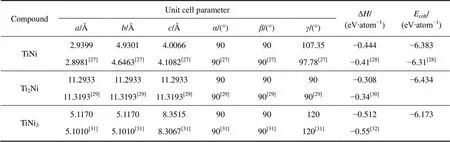
表1 TiNi、Ti2Ni和TiNi3的晶格参数、生成焓(∆H)、内聚能(Ecoh)及参考值

表2 Ti-Ni金属间化合物的独立弹性常数

2.2.2 弹性模量及延脆性

利用单晶体的弹性常数，可通过Voigt近似或Reuss近似估算由各向异性单晶体组成多晶体的弹性模量。Voigt近似和Reuss近似假设多晶体分别处于等应变状态和等应力状态，这显然与现实情况不符。HILL[35]从理论上证明，在Voigt近似和Reuss近似下分别得到的是多晶体弹性模量的上限和下限，提出采用Voigt近似和Reuss近似下的算术平均值来表征多晶体的弹性模量(即Voigt-Reuss-Hill (VRH)近似[36])，其理论估算值与实验测定值较为接近。在VRH近似下，多晶固体材料理论体模量和剪切模量的计算式如下：

(7)

式中：V、R和分别为Voigt、Reuss和Hill近似下的体模量；V、R和分别为Voigt、Reuss和Hill近似下剪切模量。利用VRH近似的计算结果，可进一步计算得到弹性模量和泊松比，即

(9)

TiNi、Ti2Ni和TiNi3金属间化合物体模量、剪切模量、弹性模量和泊松比的计算结果如表3所列，计算结果与参考文献符合得较好。结果表明，3种金属间化合物的体模量、剪切模量和弹性模量的相对大小关系是一致的，即大小依次为TiNi3、TiNi、Ti2Ni。弹性模量属于材料的内禀属性，主要与材料内部的化学键有关，是一个对显微组织结构不敏感的物理量。化学键越强则材料的弹性模量越高，如共价键材料的弹性模量通常比金属键材料的弹性模量要高。因此，在这3种金属间化合物之中，TiNi3的化学键最强，而Ti2Ni的化学键最弱。

剪切模量代表材料抵抗塑性变形的能力，体模量代表材料抵抗断裂的能力，其比值/可以用来预测材料的延(脆)性质。依据Pugh准则[38]，/值越高的材料其延展性越好，反之则越脆，其临界值为1.75。计算得到3种金属间化合物的/值如表3所列，可以看出3种金属间化合物的/值均大于临界值1.75。因此，这3种金属间化合物为延性相，延展性由大到小的排序为Ti2Ni、TiNi、TiNi3。

表3 Ti-Ni金属间化合物的力学性质(Voigt体模量BV、Reuss体模量BR、Hill体模量B、Voigt剪切模量GV、Reuss剪切模量GR、Hill剪切模量G、弹性模量E、泊松比、B/G值、弹性各向异性指数AU和硬度H)

Table 3 Mechanical properties of Ti-Ni intermetallic compounds, including Voigt’s bulk modulus BV, Reuss’s bulk modulus BR, Hill’s bulk modulus B, Voigt’s shear modulus GV, Reuss’s shear modulus GR, Hill’s shear modulus G, elastic modulus E, poisson ratio , B/G value and universal anisotropy index AU and hardness H

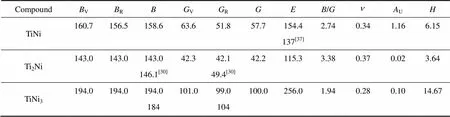
表3 Ti-Ni金属间化合物的力学性质(Voigt体模量BV、Reuss体模量BR、Hill体模量B、Voigt剪切模量GV、Reuss剪切模量GR、Hill剪切模量G、弹性模量E、泊松比、B/G值、弹性各向异性指数AU和硬度H)

CompoundBVBRBGVGRGEB/GAUH TiNi160.7156.5158.663.651.857.7154.42.740.341.166.15 137[37] Ti2Ni143.0143.0143.042.342.142.2115.33.380.370.023.64 146.1[30]49.4[30] TiNi3194.0194.0194.0101.099.0100.0256.01.940.280.1014.67 184104

2.2.3 弹性各向异性

弹性各向异性指数在工程科学中具有重要的应用，因为它与诱发微裂纹的倾向存在着极大的关 联[30]。对于不同对称性的晶体，可用通用弹性各向异性指数U予以表征，计算通式[31]如下：

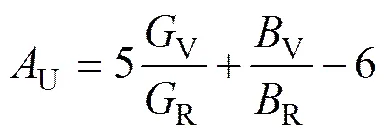
式中：U=0表示局部各向同性的单晶，U值越大则单晶的弹性各向异性越强。计算结果(见表3)表明，弹性各向异性程度主要与晶体结构类型相关。立方晶体结构的Ti2Ni的弹性各向异性程度最小，接近各向同性；单斜晶体结构的TiNi的弹性各向异性程度最大。

2.2.4 硬度

硬度是材料力学性质中的一个重要力学参数，常用来表征材料的耐磨性能，在热处理中则用来间接反映材料的强度。由于硬度同时涉及材料的弹性变形和塑性变形行为，因而其准确计算较为困难。在此，运用硬度与弹性模量的经验关系式对3种金属间化合物的硬度进行估算，计算公式[33]如下：

TiNi、Ti2Ni和TiNi3金属间化合物的硬度计算结果如表3所列，结果表明TiNi3的硬度最高，TiNi的次之，Ti2Ni的最低。

2.3 德拜温度

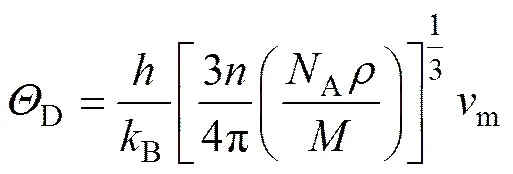
式中：为普朗克常数；B为波尔兹曼常数；为分子中的原子个数；A为阿福加德罗常数；为密度；为相对分子质量。平均弹性波速m可通过以下关系式进行计算：

(14)

式中：l和t分别为纵波波速和横波波速，其与弹性模量的关系如下：

(16)

其中：为体模量；为剪切模量。

TiNi、Ti2Ni和TiNi3金属间化合物的理论密度、纵波波速l、横波波速t、平均弹性波速m和德拜温度的计算结果如表4所列。德拜温度对应于晶格振动中弹性波的最高振动频率(德拜频率)，与晶格中原子间相互作用存在直接的关联，可以用来描述化学键键合力的强弱。德拜温度越高，则原子间的键合力越强。德拜温度的计算结果(见表4)表明TiNi3的键合力最强，TiNi的次之，Ti2Ni的键合力最弱。

表4 Ti-Ni金属间化合物的理论密度、纵波波速vl、横波波速vt、平均波速vm和德拜温度

Table 4 Theoretical density, longitudinal wave velocity vl, transverse wave velocity vt, average wave velocity vm and Debye temperature of Ti-Ni intermetallic compounds

表4 Ti-Ni金属间化合物的理论密度、纵波波速vl、横波波速vt、平均波速vm和德拜温度

Compound/(g∙cm−3)vl/(m∙s−1)vt/(m∙s−1)vm/(m∙s−1)/K TiNi6.386076.03007.33375.6510.4 Ti2Ni5.705912.62720.93065.7418.9 TiNi37.856457.43569.23976.8731.2

2.4 电子结构

为了揭示Ti-Ni金属间化合物稳定性和力学性质的本质，深入了解其化学键特性显得极为必要。为此，计算了TiNi、Ti2Ni和TiNi3金属间化合物的总态密度(TDOS)和分波态密度(PDOS)。由于材料的性质主要与费米能级附近的电子状态有关，故只取了费米能级附近区域(−9~13 eV)的总(分)态密度(见图2)。从图2可以看出，TiNi、Ti2Ni和TiNi3这3种金属间化合物具有相同的特征：1) 总态密度在费米能级处不为0，表明3种金属间化合物都具有典型的金属特性；2) 由于Ti和Ni同属于d区过渡金属，3d电子可以部分或全部参与成键，从图2可以看出3d电子对态密度的贡献最大，3p和4s电子的贡献很小；3) 在费米能级(F)以下，总态密度主要是来自Ni-d电子的贡献，而在费米能级之上则主要是Ti-d电子的贡献。

从图2(a)和2(c)可以看出，TiNi和TiNi3具有明显的赝能隙(Pseudogap)，这预示着共价键的存在。赝能隙的宽度能够反映体系共价键的强弱，显然TiNi3(赝能隙为2.56eV)的共价键要比TiNi(赝能隙为1.39eV) 的强，这也是TiNi3的硬度的TiNi的高出约1倍的原因。另一方面，共价键的强弱可以反映体系热力学稳定性的高低，共价键越强则热力学稳定性越高，因而TiNi3的热力学稳定性高于TiNi的热力学稳定性。另外，通常共价键材料的热力学稳定性通常大于金属键材料的，因而3种金属间化合物热力学稳定性的大小排序为TiNi3、TiNi、Ti2Ni，这与前面生成焓得出的结论是一致的。

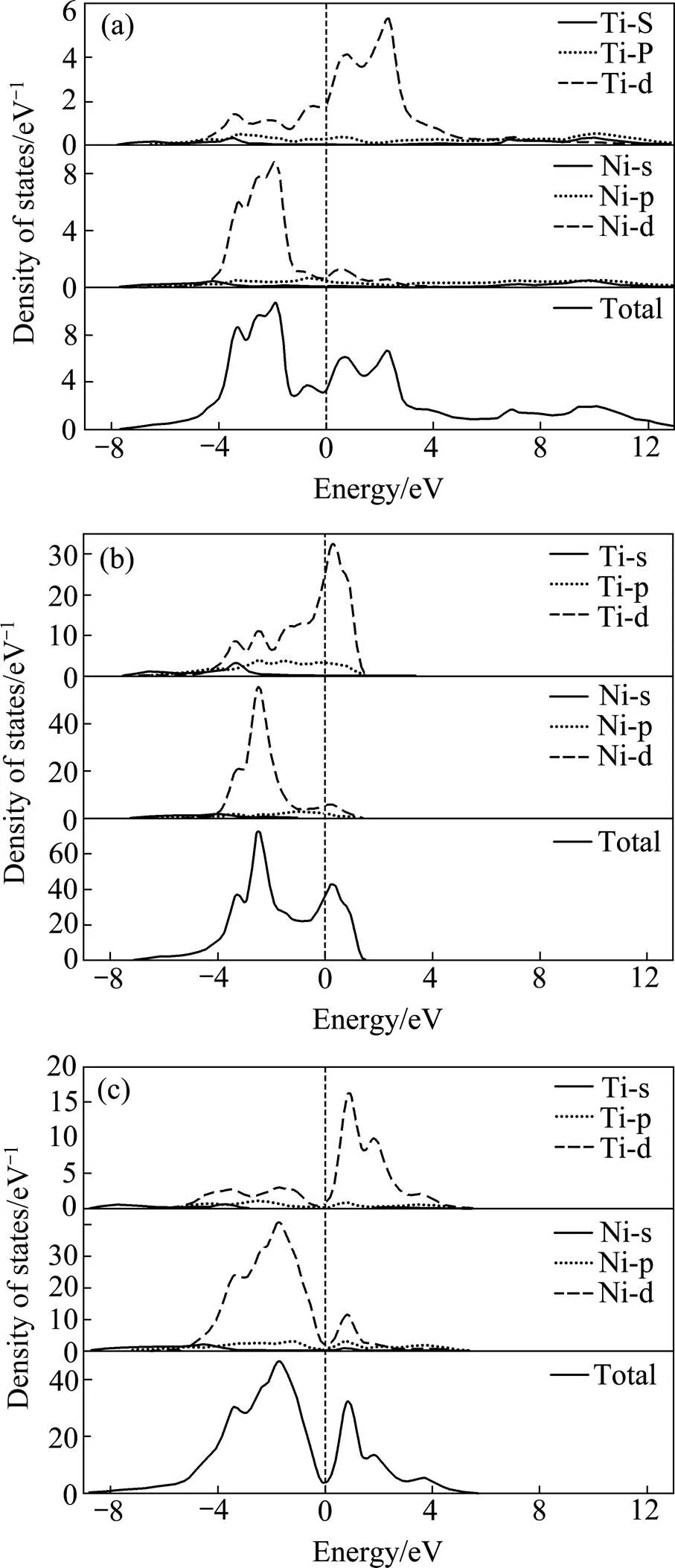
图2 Ti-Ni金属间化合物晶总态密度及分波态密度图(垂直虚线为费米能级EF (0 eV))

Ti-Ni金属间化合物的成键峰主要分布在−8.5~0 eV能量区域。对该区域的态密度进行积分，可以得到该能量区域内的成键电子数。单个原子的成键电子数越高，则说明成键作用越强烈。计算得到TiNi、Ti2Ni和TiNi3金属间化合物的平均成键电子数分别为6.997、5.994和8.501。显然，TiNi3拥有更多的成键电子数(主要源于Ni-d价电子的贡献)，因而其晶体内部原子间的键合力较高，形成了较强的化学键。由于Ni(3d84s2)能够提供比Ti(3d24s2)更多的成键电子，在Ti-Ni金属间化合物中随着Ni相对含量的增加，平均成键电子数也在增加。因此，在这3种金属间化合物中TiNi3的化学键最强，Ti2Ni的化学键最弱，这与前面弹性模量和德拜温度得出的结论一致。

金属间化合物的金属性可以如下式[35]进行计算：

式中：f为费米能级处的态密度值；e为晶胞中的价电子密度。计算得到TiNi、Ti2Ni和TiNi3金属间化合物的金属性分别为0.166、2.370和0.132，可以看出Ti2Ni的金属性远大于TiNi和TiNi3的，TiNi的金属性略大于TiNi3­的。如前面的分析，随着Ni相对含量的增加，Ti-Ni金属间化合物的共价键特征越发明显，因而TiNi3的金属性最弱。

3 结论

1) TiNi、Ti2Ni和TiNi3金属间化合物均具有热力学稳定性且容易合金化形成，合金形成能力由强到弱的排序为TiNi3、TiNi、Ti2Ni；3种金属件化合物的晶体结构在能量上和力学上也是稳定的，晶体结构稳定性由大到小的排序为Ti2Ni、TiNi、TiNi3。

2) TiNi和Ti2Ni为延性相(延展性Ti2Ni的强于TiNi的)，TiNi3的延展性较差。

3) 3种金属间化合物的硬度由大到小的排序为TiNi3、TiNi、Ti2Ni。

4) 3d电子是TiNi、Ti2Ni和TiNi3金属间化合物最主要的成键电子；在这3种金属间化合物中，随着Ni相对含量的增加，平均成键电子数在增多，热力学稳定性在增高，共价键的比例在增加，化学键的强度在增强，金属性在减弱，弹性模量、硬度和德拜温度在升高。

REFERENCES

[1] 文 潮, 刘晓新, 马艳军. 钛/钢复合板密封爆炸容器的设计与制造[J]. 中国有色金属学报, 2010, 20(S1): s972−s976. WEN Chao, LIU Xiao-xin, MA Yan-jun. Design and manufacture of explosion-containment vessel made of Ti/steel clad plate[J]. The Chinese Journal of Nonferrous Metals, 2010, 20(S1): s972−s976.

[2] 闫 力. 钛钢复合板的特点及应用领域[J]. 中国钛业, 2011(3): 12−14. LI Yan. Behaviotsard applications of Ti/steel composite sheets[J]. China Titanium Industry, 2011(3): 12−14.

[3] 高宝利, 李平仓, 华先锋, 宋 军. 钛−钢复合板在滨海电站凝汽器中的应用[J]. 钛工业进展, 2005, 22(4): 36−38. GAO Bao-li, LI Ping-cang, HUA Xian-feng, SONG Jun. Ti-steel clad plate application in steam condenser of seashore station[J]. Titanium Industry Progress, 2005, 22(4): 36−38.

[4] 王敬忠, 颜学柏, 王韦琪, 闫静亚, 容 耀, 严 平. 带夹层材料的爆炸-轧制钛钢复合板工艺研究[J]. 稀有金属材料与工程, 2010, 39(2): 309−313. WANG Jing-zhong, YAN Xue-bai, WANG Wei-qi, YAN Jing-ya, RONG Yao, Yan Ping. Titanium cladding steel plates with interlayer by explosion and rolling bonding[J]. Rare Metal Materails and Engineering, 2010, 39(2): 309−313.

[5] 刘继雄, 张杭永, 郭佳林, 王鼎春, 刘润生, 高 颀, 江海涛. 界面金属间化合物对钛钢复合板力学行为的影响[J]. 中国钛业, 2014(2): 24−28. LIU Ji-xiong, ZHANG Hang-yong, GUO Jia-lin, WANG Ding-chun, LIU Run-sheng, GAO Qi, JIANG Hai-tao. Effects of interfacial intermetallic compounds on mechanical behaviors of titanium clad steel plates[J]. China Titanium Industry, 2014(2): 24−28.

[6] Jiang H T, Kang Q, Yan X Q. A novel diffusion model considering curvature radius at the bonding interface in a titanium/steel explosive clad plate[J]. International Journal of Minerals Metallurgy & Materials, 2015, 22(9): 956−965.

[7] Sam S, Kundu S, Chatterjee S. Diffusion bonding of titanium alloy to micro-duplex stainless steel using a nickel alloy interlayer: Interface microstructure and strength properties[J]. Materials & Design, 2012, 40(5): 237−244.

[8] Morse S L, Mcglynn J J. Titanium clad steel and process for making: US, US4023936[P]. 1977.

[9] Murayama J, Komizo Y. Titanium-clad steel and a method for the manufacture thereof: US, US4839242[P]. 1989.

[10] Peng H, Zhang J, Zhou R, LI X. Diffusion bonding technology of a titanium alloy to a stainless steel web with an Ni interlayer[J]. Materials Characterization, 1999, 43(5): 287−292.

[11] Shiue R K, Wu S K, Chan C H, Huang C S. Infrared brazing of Ti-6AI-4V and 17-4 PH stainless steel with a nickel barrier layer[J]. Metallurgical and Materials Transactions A, 2006, 37(7): 2207−2217.

[12] Kundu S, Chatterjee S, Olson D, Mishra B. Effects of intermetallic phases on the bond strength of diffusion-bonded joints between titanium and 304 stainless steel using nickel interlayer[J]. Metallurgical and Materials Transactions A, 2007, 38(9): 2053−2060.

[13] Kundu S, Sam S, Chatterjee S. Interfacial reactions and strength properties in dissimilar titanium alloy/Ni alloy/microduplex stainless steel diffusion bonded joints[J]. Materials Science and Engineering A, 2013, 560(2): 288−295.

[14] Kundu S, Anand G, Chatterjee S. Diffusion bonding of 17-4 precipitation hardening stainless steel to Ti alloy with and without Ni alloy interlayer: Interface microstructure and mechanical properties[J]. Metallurgical & Materials Transactions A, 2013, 44(5): 2196−2211.

[15] Kundu S, Chatterjee S. Interfacial microstructure and mechanical properties of diffusion-bonded titanium-stainless steel joints using a nickel interlayer[J]. Materials Science and Engineering A, 2006, 425(S1/2): 107−113.

[16] Thirunavukarasu G, Kundu S, Mishra B, Chatterjee S. Effect of bonding temperature on interfacial reaction and mechanical properties of diffusion-bonded joint between Ti-6Al-4V and 304 stainless steel using nickel as an intermediate material[J]. Metallurgical and Materials Transactions A, 2014, 45(4): 2067−2077.

[17] 黄 利. 加镍中间层的表面自纳米化钛合金/不锈钢扩散焊接[D]. 重庆: 重庆大学, 2011. HUANG Li. Diffusion bonding of surface self-nanocrystallined Ti alloy and stainless steel with a Ni interlayer[D]. Chongqing: Chongqing University, 2011.

[18] Hinotani S, Ohmori Y. The microstructure of diffusion- bonded Ti/Ni interface[J]. Materials Transactions Jim, 1988, 29(2): 116−124.

[19] 董 凤, 陈少平, 樊文浩, 胡利方, 孟庆森. 电场激活Ti/Ni扩散偶连接界面相变规律与力学性能的研究[J]. 稀有金属材料与工程, 2015, 44(2): 349−354. DONG Feng, CHEN Shao-ping, FAN Wen-hao, HU Li-fang, MENG Qing-sen. Phase transformation and mechanical performance of interface between Ti/Ni diffusion bonding couples activated by electric field[J]. Rare Metal Materails and Engineering, 2015, 44(2): 349−354.

[20] Hinotani S, Ohmori Y. The microstructure of diffusion- bonded Ti/Ni interface[J]. Materials Transactions Jim, 1988, 29(2): 116−124.

[21] Emadinia O, Simões S, Viana F, Vieira M F, Cavaleiro A J, Ramos A S, Vieira M T. Cold rolled versus sputtered Ni/Ti multilayers for reaction-assisted diffusion bonding[J]. Welding in the World, 2016, 60(2): 337−344.

[22] Clark S J, Segall M D, Pickard C J, Hasnip P J, Probert M J, REFSON K, PAYNE M C. First principles methods using CASTEP[J]. Zeitschrift Für Kristallographie, 2005, 220(5/6): 567−570.

[23] Perdew J P, Wang Y. Accurate and simple analytic representation of the electron-gas correlation energy[J]. Physical Review B, 1992, 45(23): 13244−13249.

[24] Monkhorst H J, Pack J D. Special points for Brillouin-zone integrations[J]. Physical Review B, 1976, 13(12): 5188−5192.

[25] Hammer B, Hansen L B, Norskov J K. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals[J]. Physical Review B, 1999, 59(11): 7413−7421.

[26] Fischer T H, Almlof J. General methods for geometry and wave function optimization[J]. Journal of Physical Chemistry, 1992, 96(24): 9768−9774.

[27] Kudoh Y, Tokonami M, Miyazaki S, Otsuka K. Crystal structure of the martensite in Ti-49.2 at.%Ni alloy analyzed by the single crystal X-ray diffraction method[J]. Acta Metallurgica, 1985, 33(11): 2049−2056.

[28] Batalović K, Koteski V, Stojić D. Hydrogen storage in martensite Ti-Zr-Ni alloy: A density functional theory study[J]. Journal of Physical Chemistry C, 2013, 117(51): 26914−26920.

[29] Mueller M H, Knott H W. The crystal structures of Ti2Cu, Ti2Ni, Ti4Ni2O, and Ti4Cu2O[J]. Transactions of the Metallurgical Society of Aime, 1963, 227: 674−678.

[30] Toprek D, Belosevic-cavor J, Koteski V. Ab initio studies of the structural, elastic, electronic and thermal properties of NiTi2intermetallic[J]. Journal of Physics & Chemistry of Solids, 2015, 85: 197−205.

[31] Taylor A, Floyd R W. Precision measurements of lattice parameters of non-cubic crystals[J]. Acta Crystallographica, 1950, 3(4): 285−289.

[32] Chen Q, Huang Z, Zhao Z, Hu C. First-principles study on the structural, elastic, and thermodynamics properties of Ni3X (X: Al, Mo, Ti, Pt, Si, Nb, V, and Zr) intermetallic compounds[J]. Applied Physics A, 2013, 116(3): 1−12.

[33] BORN M, HUANG K. Dynamical theories of crystal lattices[M]. New York: Oxford University Press, 1956: 141−160.

[34] COWLEY R A. Acoustic phonon instabilities and structural phase transitions[J]. Physical Review B, 1976, 13(11): 4877−4885.

[35] HILL R. The elastic behaviour of a crystalline aggregate[J]. Proceedings of the Physical Society, 1952, 65(5): 349−354.

[36] BOND W L. Physical properties of crystals: Their representation by tensors and matrices[J]. Journal of Physics & Chemistry of Solids, 1957, 3: 338.

[37] ŠESTÁK P, ČERNÝ M, POKLUDA J. Elastic properties of B19’ structure of NiTi alloy under uniaxial and hydrostatic loading from first principles[J]. Strength of Materials, 2008, 40(1): 12−15.

[38] PUGH S F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals[J]. London Edinburgh & Dublin Philosophical Magazine & Journal of Science, 1954, 45(367): 823−843.

[39] FRANTSEVICH I N, VORONOV F F, BOKUTA S A. Elastic constants and elastic moduli of metals and insulators: handbook[M]. Kiev: Naukova Dumka, 1983: 60−180.

[40] TVERGAARD V, HUTCHINSON J W. Microcracking in ceramics induced by thermal expansion or elastic anisotropy[J]. Journal of the American Ceramic Society, 1988, 71(3): 157−166.

[41] RANGANATHAN S I, OSTOJA-STARZEWSKI M. Universal elastic anisotropy index[J]. Phys Rev Lett, 2008, 101(5): 055504.

[42] YOUSEF E S, EL-ADAWY A, EL-KHESHKHANY N. Effect of rare earth (Pr2O3, Nd2O3, Sm2O3, Eu2O3, Gd2O3and Er2O3) on the acoustic properties of glass belonging to bismuth-borate system[J]. Solid State Communications, 2006, 139(3): 108−113.

[43] MUSIC D, HOUBEN A, DRONSKOWSKI R, SCHNEIDER J M. Ab initio study of ductility in M2AlC (M=Ti, V, Cr)[J]. Physical Review B, 2007, 75: 174102.

[44] LI Y F, GAO Y M, XIAO B, MIN T, FAN Z J, MA S Q, XU L L. Theoretical study on the stability, elasticity, hardness and electronic structures of W-C binary compounds[J]. Journal of Alloys & Compounds, 2010, 502(1): 28−37.

(编辑 王 超)

First-principles calculations of electronic structure and mechanical properties of Ti-Ni intermetallic compounds

WANG Peng1, LI Jun1,LIN Chong-zhi1, YANG Liu1, PENG Lin1, WANG Ying1, XIAO Chong1, CHEN Jing-chao2

(1. Pangang Group Research Institute Co., Ltd., State Key Laboratory of Vanadium and Titanium Resources Comprehensive Utilization, Panzhihua 617000, China;2. Key Laboratory of Advance Material of Rare Precious and Nonferrous Metals, Kunming University of Science and Technology, Kunming 650093, China)

The crystal structure, enthalpy of formation, cohesive energy, mechanical properties, Debye temperature and electronic structure of TiNi, Ti2Ni and TiNi3intermetallic compounds were calculated by using first-principles ultrasoft pseudo-potential approach of the plane wave based on density functional theory (DFT). The calculated results show that three intermetallic compounds all have thermodynamic stability and are easy to form alloy. TiNi3has the strongest alloys forming ability. The crystal structures of those intermetallic compounds are stable in energy and mechanics, the stability in descending order are as follows: Ti2Ni, TiNi, TiNi3. TiNi and Ti2Ni are ductile, and the ductility of Ti2Ni is significantly higher than that of TiNi. TiNi3has a poor ductility. The 3d electronics are the mainly bonding electrons. As the increase of relative amounts of Ni in those intermetallic compounds, the average bonding electrons are growing, the strength of chemical bonds enhance, the metallicity weakens. This leads to gradually increase of the elasticity modulus, hardness and Debey temperature.

Ti-Ni; intermetallic compound; electronic structure; mechanical property; first-principle

2015-09-07; Accepted date:2016-03-15

WANG Peng; Tel: +86-8123380654; E-mail:scwangp@gmail.com

1004-0609(2016)-12-2546-09

TB31

A

2015-09-07；

2016-03-15

王 鹏，工程师，硕士；电话：0812-3380654；E-mail: scwangp@gmail.com