基于多模式降水量预报的浙江省统计降尺度研究*

黎玥君 余贞寿

(浙江省气象科学研究所，浙江 杭州 310008)

基于多模式降水量预报的浙江省统计降尺度研究*

黎玥君 余贞寿

(浙江省气象科学研究所，浙江 杭州 310008)

基于欧洲中期天气预报中心(ECMWF)、美国全球集合预报系统(GFS)、日本气象厅(JMA)3个中心3～96 h预报时效的降水量预报资料，以及浙江省1957个高密度的自动站观测资料，对数值模式预报结果进行统计降尺度处理。首先利用线性回归方法对插值后的预报结果进行降尺度订正，然后把3个数值预报的降尺度结果进行消除偏差集合平均，最后得到多模式集成的降水量预报场。结果表明，统计降尺度订正后的预报结果比直接插值更加准确，多模式集成的预报效果优于单模式结果，其改进效果随预报时效的延长减小。

降水量预报；统计降尺度；多模式集成

0 引 言

与传统的天气分析和预报相比，数值预报具有能够反映大气物理规律的特性，因此它成为天气预报以及气候变化影响评估的重要技术基础，近年来数值天气预报技术不断发展，已由单个模式的确定性预报向多成员、多模式的集合预报转变[1]。这一发展趋势为其在降水量预测以及气象水文风险预报方面开拓了广泛的应用前景。目前大部分模式的空间分辨率还比较低，有两种方法可以弥补这方面的不足，一是发展更高分辨率的气候模式，另一种是统计降尺度法把低分辨率的全球数值预报结果转化为高分辨率的预报变量，建立低分辨率的模式结果与高分辨率的预报变量间的函数关系[2]。前人对统计降尺度有了一些研究，Wilby，et al[3]对比了6种降尺度方法(两种神经网络，两种天气发生器，两种基于涡度的回归方法)在美国的模拟效果，发现回归方法模拟能力最好。Krishnamurti，et al[4]将超级集合预报方法应用到印度季风区，并首次提出多模式集合与统计降尺度相结合的方法，预报技巧获得了明显提高。Voisin，et al[5]将卫星遥感资料与集合预报的降尺度结果相结合，用作实测场较稀疏的美国俄亥俄河流域的降水预报，结果发现，无论是在径流分布还是在每日径流量预测方面，经过降尺度法订正之后的预报结果，都比单纯的插值结果更加准确。王亚男等[6]对2007年夏季中国降水量预报进行降尺度试验，并将多模式集合预报与降尺度方法相结合，发现多模式集成的预报效果优于单模式预报。

统计降尺度方法中的回归分析、主成份分析、典型相关分析等线性函数转换法对于月以上时间尺度的气候要素的模拟效果较好，对于日降水量预报降尺度结果，由于日降水量具有不连续性、非正态分布等特点[7]，这种线性方法常会出现空报、漏报以及极值低估等现象。马培迎[8]以预报值为变量，利用逻辑回归模型，将天气分为有雨和无雨，再对有雨的概率预报进行修正，以提高预报精度。不同的模式针对同一个预报对象会得出不同的预报结果，为了得到一个确定的预报结论，多模式集成技术就是一个充分利用各中心模式预报结果以减小模式系统性误差的有效途径[9]。国内外大量的研究表明，多模式超级集合可有效地减小预报的均方根误差[10-15]。

1 资料与方法

1.1 资料来源

预报资料选用ECMWF(51个成员)、GFS(21个成员)、JMA(51个成员)3个预报中心全球集合预报模式的3 h累计降水量预报，起报时间为12时(世界时)，预报时段取2015年6月1日—8月31日，间隔3 h。ECMWF的空间分辨率为0.125×0.125，GFS的空间分辨率为0.5×0.5，JMA的空间分辨率为0.5×0.5。

把ECWMF、GFS、JMA的降水量的数值预报结果，提取浙江省资料，然后统一双线性插值到0.025×0.025精度的网格上。

实况资料为浙江省自动站降水观测资料(1957个站)，时间范围为2015年6月1日—8月31日，时间间隔为1 h。

将实况资料合成与3个中心集合预报资料的12时(世界时)起报的3 h累计降水量，并插值到0.025×0.025精度的网格上，作为高分辨率的降水量观测值，用来检验预报效果。

1.2 方 法

1.2.1 双线性插值法

双线性插值(Bilinear Interpolation)，又称为双线性内插。在数学上，双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。 假设函数f在点P=(x，y)的值未知，而已知函数f 在Q11= (x1，y1)、Q22=(x1，y2)，Q21=(x2，y1) 以及Q22= (x2，y2)4个点的值(图1)

图1 双线性插值示意图

第一步：x方向的线性插值，插入蓝色点标注的数据

第二步：对x方向插值后的数据进行y方向的插值

这样就得到了所求的P 点的值。利用双线性插值，首先将低分辨率的数值预报结果，插值到更加精细化的网格上。

1.2.2 统计降尺度订正法

本文所用的统计降尺度模型为一元线性回归，即选取一定长度的训练期，建立模式预报值与“观测值”间的统计关系式：

Yi =a Xi + b

其中，a，b 为回归系数，Xi 为插值后的ECMWF模式预报序列，Yi 为高密度的观测资料。在训练期确定回归系数a，b 之后，利用该关系式，对模式降水量的预报值进行降尺度订正。

1.2.3 消除偏差集合平均法

利用消除偏差集合平均法(Bias-removed Ensemble Mean)对3个中心的预报结果进行多模式集成。集成的关系式如下：

1.2.4 检验方法

1.2.4.1 ETS评分

其中，a是预报准确的，b是漏报的，c是空报的，d是实况和预报均没有出现降水的情形。ETS评分可针对某个量级以上的降水进行评分。ETS>0时为有技巧预报，ETS<=0时为无技巧预报，ETS=1时为最佳预报。

另外，用到的检验方法还有均方根误差(RMSE)，它反映误差的平均大小。

1.2.4.2 交叉样本检验

研究过程中将试验序列分为两端，包括“训练期”和“预报期”，采用交叉样本检验法进行模拟，即从试验资料序列的第1个样本开始，依次留1个样本作预报检验，余下样本均作为“训练期”样本进行模拟。

2 降尺度方法对单模式的订正

为了提高模式预报的准确性，利用线性回归方法对降水量预报做降尺度订正。先利用双线性插值将低分辨率的模式预报值插值到细网格上，通过训练期的预报值和观测值建立回归方程，根据该方程对结果进行订正。

为了研究统计降尺度方法对预报误差的改进效果，计算出浙江省范围内预报场与观测场之间的格点平均RMSE和距平相关系数ACC。图2左列给出了3个预报中心3～60 h预报时效的3 h累积降水量降尺度订正前后的距平相关系数在80 d预报期内的平均值。如图2所示，降尺度订正之后，3个预报中心3～60 h预报的ACC均有所提高，其中改进最大的是EC预报的36 h预报结果，ACC提高了将近0.25，3个中心对36～60 h的预报的提高不是很明显，这可能与预报本身的准确性有关。

再计算格点平均的均方根误差RMSE，图2右列给出了3个预报中心3～60 h预报时效的3 h累积降水量降尺度订正前后的均方根误差在80 d预报期内的平均值。如图所示，降尺度订正之后，3个预报中心的RMSE均有所减小，ECMWF中心3～60 h预报的原始误差相对较大，改进幅度是3个预报中心里最明显的。GFS和JMA中心都是在3～30 h的预报改进幅度比较大，随着预报时效的增加，RMSE减小的幅度下降，可能与预报中心本身的预报准确率有关。

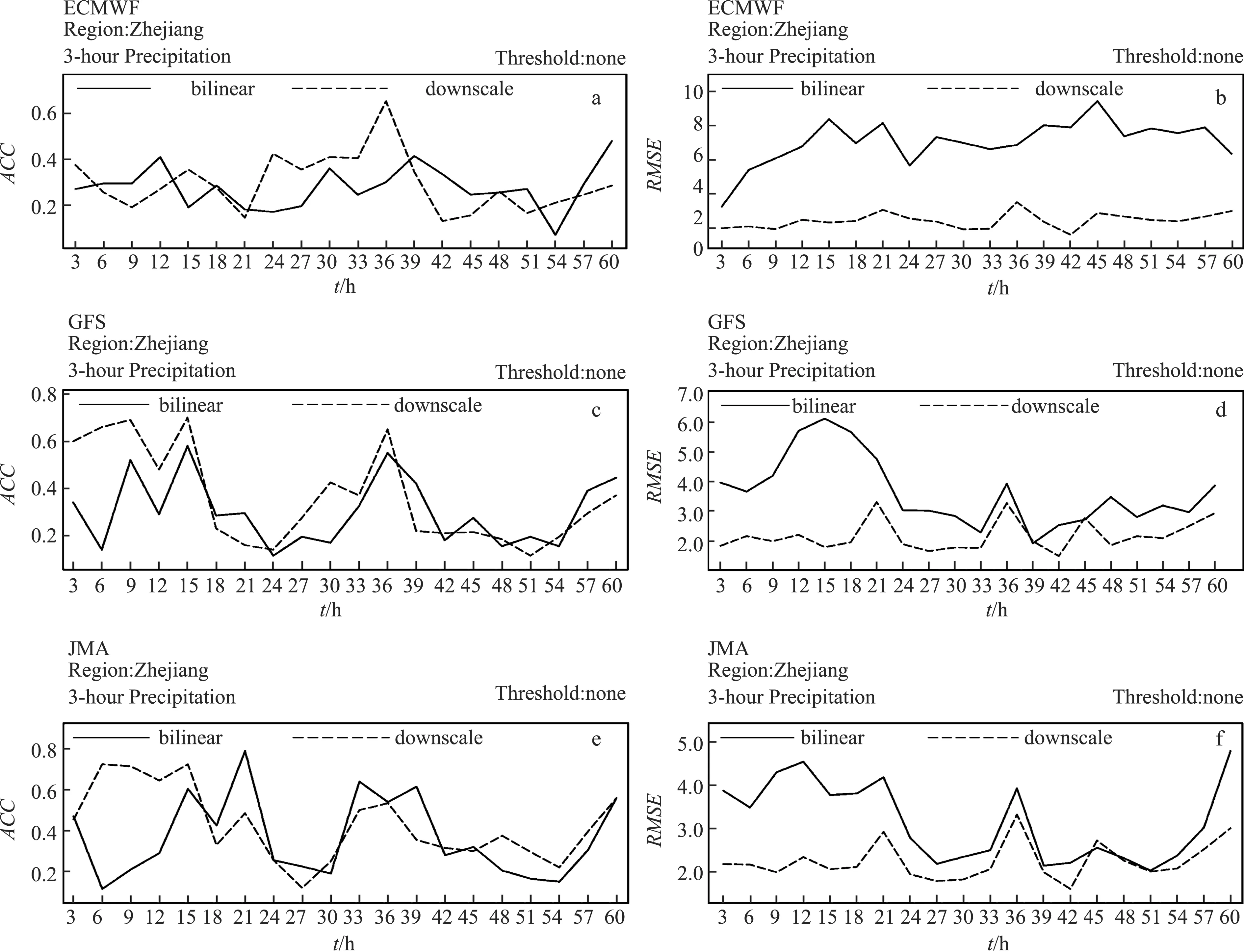
图2 3个预报中心3～60 h累积降水量降尺度订正前后的距平相关系数ACC(左a、c、e)和均方根误差RMSE(右b、d、f)

通过以上分析可以看出，与直接插值的结果相比，经过降尺度订正之后的预报值与实况值之间的相关程度提高，均方根误差明显减小。不同模式预报中心、不同预报时效以及不同的降水量级，改进程度各不相同。总体而言，订正之后的预报场更加接近实况场。因此，在业务预报中将低分辨率的模式预报结果插值成高分辨率之后，再通过线性回归进行拟合，能够获得具有更高准确率的精细化预报结果。

3 多模式集成研究

在多模式集成进行之前，首先要对训练期长度进行调试，选取最佳训练期。在整个资料时间序列中将训练期长度从1 d到80 d进行调整，并分别计算不同训练期长度对应的RMSE(图略)。通过计算发现，不同的预报时效，不同训练期长度对应的RMSE整体趋势是一致的。10 d 之内，随着训练期变长，RMSE逐渐减小，10～45 d左右的训练期长度对应的RMSE变化较为平缓，50～65 d之中，随着训练期的增长，RMSE反而有所增加了，到了65 d之后，训练期越长，误差越小。结果表明，对于大多数预报时效，65 d左右的训练期对应的误差是最小的。因此，为了能够达到最佳集成效果，同时充分利用所有资料，多模式集成的训练期长短选择同样选用交叉样本检验。

将3个预报中心的降尺度结果进行消除偏差集合平均，利用3个预报中心集成后的结果进行检验。分别计算研究时段内3个单模式以及多模式集成降尺度3～60 h预报时效的3 h累计降水量预报值与实况值之间的ACC和RMSE。图3给出的是80 d的平均结果。从图3a中可以看出，多模式集成之后，3～21 h预报时效的均方根误差与单模式相比均有了明显的减小，其中09 h预报时效改善明显，而24～60 h预报时效集成之后的结果与最好的单中心相比无明显改善，39 h预报时效甚至出现了RMSE大于GFS的现象。再对比ACC(图4b)的值可以发现，多模式集成之后，3～60 h预报时效的距平相关系数与单模式相比均有了提高，仅有几个预报时效的集成结果与单预报中心结果相比无明显改善。总体来看，多模式集成之后的预报结果好于单模式的预报结果。

图3 3个预报中心降尺度以及多模式集成降尺度3h累计降水量3～60h预报时效的均方根误差(a)、距平相关系数(b)

图4给出了3个预报中心以及多模式集成降尺度3h预报时效的不同等级降水量的ETS评分。如图4所示，不同雨量级的降水多模式集合降尺度的ETS评分总体高于其他单模式，比起最好的单模式结果平均改进了10%左右。各个预报中心ETS评分随着降水等级的增大有先升后降的趋势，1 mm以上的雨量等级评分最高，多模式集成降尺度的评分随着降水等级的增大在减小。对于3.5 mm以上雨量的评分各个预报中心及集成结果的ETS评分减小的幅度很大，5.0 mm以上雨量的ETS评分为空值，其原因除了插值平滑掉部分极值以外，可能还与集合预报资料本身对降水极值预报的缺陷有关。

图4 3个预报中心降尺度以及多模式集成降尺度 3 h预报时效3 h累积降水量对不同雨量 等级以上降水的ETS评分

以上研究表明，消除偏差集合平均能够有效地降低RMSE值，尤其对于24 h以内的预报，整体预报效果比所有单模式的改进程度要高。在日常业务中，采用多模式降水预报的集成，不仅可以避免对单个模式之间的缺陷，还可以提供一个更稳定可靠的确定性预报结果。多模式集成降尺度对0～3.5 mm量级的ETS评分较好，对于3.5 mm以上量级的预报效果改进还有待进一步研究。

4 结 语

对2015年6月1日至2015年8月31日期间，利用ECMWF、GFS、JMA 3个预报中心3 h累计降水量的模式预报值以及相应的实况自动站资料，对浙江省范围内的降水进行降尺度预报研究，结果表明：

1)通过与观测资料的对比，发现降尺度模型的结果，与预报期内直接插值的结果相比，降尺度订正之后的预报值与实况值之间相关程度提高，均方根误差明显减小，不同预报中心、不同预报时效改进程度各不相同。直接插值和回归降尺度后的预报误差随着预报时效的延长而增大，且回归降尺度后的改善效果与各单模式自身的预报效果有关。

2)利用消除偏差集合平均对回归降尺度后的结果进行多模式集成，首先进行最优训练期的选取，综合分析多时效的均方根误差表明，20时起报的降水的最优训练期选为65 d。

3)多模式集成将不同模式的预报结果进行的综合集成，达到了减小各个单模式的系统误差的效果。利用BREM集成方法获得的预报技巧在3～24 h预报时效高于其他所有单模式，其改进程度随着预报时效的延长逐渐减小。各个预报中心ETS评分随着降水量级的增大都有先升后降的趋势，多模式降尺度的评分改进幅度也随之减小，对于5.0 mm以上量级的降水量的预报还有待进一步研究。

[1] 杜钧，陈静.单一值预报向概率预报转变的基础:谈谈集合预报及其带来的变革[J].气象,2010,36(11):1-11.

[2] 范丽军,符淙斌,陈德亮.统计降尺度法对未来区域气候变化情景预估的研究进展[J].地球科学进展,2005,20(3):320-329.

[3] Wilby R L,Wigley T M L,Conway D,et al.Statistical downscaling of general circulation model output:A review of methods and limitations[J].Progress in Physical Geography,1997,21(4):530-548.

[4] Krishnamurti,T N,Mishra A K,Chakraborty A,et al.Improving global model precipitation forecasts over India using downscaling and the FSU superensemble.Part I:1-5-Day forecasts[J]. Monthly Weather Review,2009,137:2713-2735.

[5] Voisin N,Pappenberger F.Application of a medium-range global hydrologic probabilistic forecast scheme to the Ohio River basin[J].Weather and Forecasting，2011，26(4):425-446.

[6] 王亚男,智协飞.多模式降水集合预报的统计降尺度研究[J].暴雨灾害,2012,31(1):1-7.

[7] 范丽军，符淙斌，陈德亮.统计降尺度法对未来区域气候变化情景预估的研究进展[J].地球科学进展,2005,20(3):320-329.

[8] 马培迎.应用贝叶斯原理修正降水概率预报[J].气象科技,1999(1):45-48.

[9] 段明铿,王盘兴.集合预报方法及应用进展综述[J].南京气象学院报,2004,27(2):279-288.

[10] Krishnamurti T N,Kishtawal C M,LaRow T E,et al.Improving weather and seasonal climate forecasts from multimodel superensemble[J].Science,1999，85(5433):1548-1550.

[11] Kumar V,Krishnamurti T N,Fiorino M,et al.Multimodel superensemble forecasting of tropical cyclones in the Pacific[J]. Mon Wea Rev，2003,131(3):574-583.

[12] Ross R S,Krishnamurti T N.Reduction of forecast error for global numerical weather prediction by The Florida State University Superensemble[J]. Meteor Atmos Phys.2005,88(3-4):215-235.

[13] 智协飞，林春泽,白永清，等.北半球中纬度地区地面气温的超级集合预报[J].气象科学，2009,29(5):569-574.

[14] 林春泽,智协飞,韩艳,等.基于TIGGE资料的地面气温多模式超级集合预报[J].应用气象学报,2009,20(6):706-712.

[15] 崔慧慧，智协飞.基于TIGGE资料的地面气温延伸期多模式集成预报[J].大气科学学报，2013,36(2):165-173.

2016-07-28

*资助项目：浙江省气象科技计划项目(2015QN02)