基于凸优化基追踪算法的线性调频信号参数估计
2017-01-16周青松张剑云
夏 杰,周青松,张剑云,董 玮
(解放军电子工程学院,安徽 合肥 230037)
基于凸优化基追踪算法的线性调频信号参数估计
夏 杰,周青松,张剑云,董 玮
(解放军电子工程学院,安徽 合肥 230037)
针对传统宽带线性调频信号参数估计精度不高的问题,提出了基于凸优化基追踪算法的线性调频信号参数估计方法。该方法利用Gabor原子良好时频特性,以l1范数稀疏正则最小二乘模型为目标函数求解稀疏Gabor原子进行参数估计。仿真实验证明,该方法具有原子的稀疏性好,对原信号重构精度高和参数估计准确的特点。
凸优化基追踪;线性调频信号;时频分析;参数估计
0 引言
线性调频信号在雷达、通信、制导等军事领域有着广泛的应用。对线性调频信号的参数估计一直是电子侦察领域的重要问题。传统的估计方法大都以最大似然估计[1]为基础。最大似然估计方法精度高,然而搜索量极大,无法应对现代宽带信号。近年来,诸如分数阶傅里叶变换(FrFT)[2-3]、压缩感知[4-7]等方法被大量应用。压缩感知理论利用了信号的稀疏特性,其中贪婪算法(MP)[5]、正交匹配算法(OMP)[7-8]计算复杂度低,可是精度不高。分数阶傅里叶变换可被理解为线调基的分解,在不同阶数的u域上分离多分量的信号与噪声,然而在不同阶数上存在偏差需进行补偿, 影响了估计精度。本文针对上述问题,提出了基于凸优化基追踪算法的线性调频信号参数估计方法。
1 信号模型与凸优化基追踪算法理论
1.1 线性调频信号模型
白噪声下单分量线性调频信号数学表达式为:
y(t)=Aexp(jπμ0t2+2jπf0t)+w(t)
(1)
其中,信号幅度为A,初始频率为f0,调制斜率为μ0,噪声w(t)为加性高斯白噪声。若对信号均匀采样n个点,采样间隔为Δt。则观测信号向量为:
y=[y(0),y(1),…,y(n-1)]T
y(i)=Aexp[jπ(μ0Δt2i2+2f0Δti)]+
w(Δt·i),i=0,1,2,…,n-1
(2)
1.2 过完备字典构建
在信号的稀疏描述中,挑选适合的基函数构建字典尤为重要。字典的选择直接影响到描述系数的稀疏性以及重构信号的精度。过完备字典指字典中的原子个数大于信号维数并包含信号中各向量张成的整个空间。在目前的字典中,过完备字典通过增加原子个数来增加系统冗余度,较之其他字典提高对观测信号逼近的灵活性。
本文选择Mallat和Zhang提出的过完备Gabor原子字典[5],见图1。由测不准原理得,有限能量任意信号,其时宽与带宽存在以下关系:
(3)
当不等式取等号时,信号为高斯函数e-πt2,具有最小时宽带宽积。Gabor原子为一系列调制的高斯函数,具有最小的时宽带宽积,因而具有最好的时频聚集特性。其数学表达式为:
e-(t-τ)2/σ2cos(wt+φ)
(4)
每个Gabor原子通过参数γ=(τ,w,φ)来描述,其中σ为脉冲宽度,τ为脉冲时间中心,w为瞬时频率,φ为相角。
围绕目标信号形式构建复信号基。首先,对Gabor函数高斯包络e-(t-τ)2/σ2进行时域调制:基函数取相同的脉宽σ;中心时间τ按照观测时间长度均匀取m个点得到时域基。然后,在时域基上对高斯包络进行频率调制得复信号基函数e-(t-τ)2/σ2exp(j2πf1tk)。k为频率划分点(kmin≤k≤kmax),取整数;单位频率间隔f1的选取保证信号的最高频率fmax与最低频率fmin在区间[f1·kmin,f1·kmax]内。此处,m取501,k取30,φ取为0。对应每个中心时间点,一共(30+1)个复频点(其中一个为0频)。

(a)字典矩阵A(共501×31个原子)

(b)中心时间为0时复频点内部排列图1 本文构建的Gabor过完备字典矩阵AFig.1 The proposed Gabor over-complete dictionary
1.3 l1范数稀疏正则最小二乘模型
凸优化基追踪算法将信号在过完备字典上进行展开,获得稀疏的原子,利用这些原子完成对原始信号的重构。鉴于此思想,将信号模型进一步构建为基于混合l0范数的稀疏正则最小二乘模型:
minimize ‖Ax-y‖2+γ‖x‖0
(5)
其中,‖Ax-y‖2代表数据的拟合误差, γ‖y‖0代表Gabor原子向量稀疏度的衡量, γ是加权因子,它实现对数据的拟合质量和原子向量稀疏度的平衡与折中,从而兼顾两者的性能。
但是式(5)中包含了l0范数的优化问题,这是一个整数优化的NP难问题,现有理论难以给出一个有效的求解方法。因此考虑将其松弛为一个可有效求解的凸优化问题。由于l1范数是在所有 lp范数( ‖·‖p,p≥1)当中最接近l0范数的凸范数,因此将上述模型进一步松弛为混合l1范数的稀疏正则最小二乘模型[4]:
minimize ‖Ax-y‖2+γ‖x‖1
(6)
因此如何求解该模型是本问题的难点所在。由于优化模型中的目标函数是两个不可微函数的混合,一般优化方法难以求解。但是该问题是一个典型的凸优化问题,所以将其转化为二阶锥规划(SOCP, second-order cone programming)以便原对偶内点算法对其进行有效求解,并且所获得解一定为该优化模型的全局最优解。
1.4 l1范数稀疏正则最小二乘模型的求解
将标准的k维二阶锥记为:
(7)
并且当k=1时,定义一维二阶锥为cone1={t|t∈R,0≤t}。
为了便于转化,可将式(6)与下式等价:
minimize ξ subject to ‖Ax-y‖2≤σ
γ‖yk‖2≤ϖk,k=1,…,K
σ+ϖ1+…+ϖK≤ξ
(8)
令A=Ar+jAi,x=xr+jxi,y=yr+jyi,v=[1,01×3K+1]T,w=[ξ,σ,ϖ1,…,ϖK,xr1,…,xrK,xi1,…,xiK]T,vs=[0,…,1,0,…,0]T,v1=[0,1,01×3K]T,E′为K维的全1列向量,其中,v1,w,v和vs均为3K+2维的列向量,vs表示向量中第s个元素为1,其余元素均为0,s=1,…,K。则式(8)的目标函数可以表示为vTy,其余各个约束条件的转化形式为:
‖Ax-y‖2≤σ ⟺
‖(Arxr-Aixi-yr)+j(Arxi+Aixr-yi)‖2≤σ ⟺
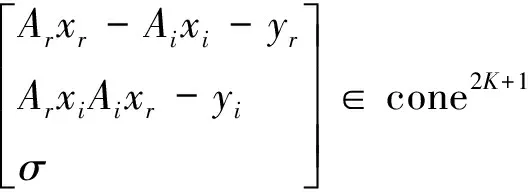
γ‖xk‖2≤ϖk⟺γ‖xr,k+jxi,k‖2≤ϖk⟺
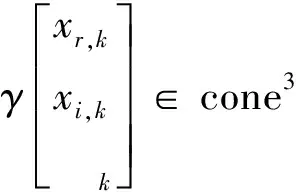
σ+ϖ1+…+ϖK≤ξ ⟺ξ-ϖ1-…-ϖK-σ≥0⟺
至此可以构造出式(6)的SOCP模型为:
minimize vTw
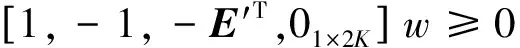
(9)
对于式(9)可以采用MatLab中的CVX工具箱进行求解。
2 凸优化基追踪算法参数估计原理与步骤
2.1 参数估计原理
根据测不准原理,Gabor原子在时频域具有良好的聚集特性。若将信号分解为Gabor原子的线性组合,那么可以充分地揭示信号的脉内特征。假设信号y经稀疏分解为k个Gabor原子,这k个原子f(τi,wi,φi)|i=1,2,…,k包含了原信号的特征以及绝大部分的能量。对这k个原子进行时频分析,进而可提取出其中的参数信息。
图2为包含三个不同分量线调信号时频图(下方为时域图,右侧为频域图),它由MP算法在Gabor字典上分解的原子经Wigner变换相加得,参见文献[5]。可见,属于同一个线调信号的原子排列在同一条直线上,直线显示了信号频率随时间的变化,直线的斜率即为该线调信号的调频斜率。而直线两端的两个原子分别表示起止和终止频率。故通过获取Gabor原子的时频位置,可求得信号的频率信息。
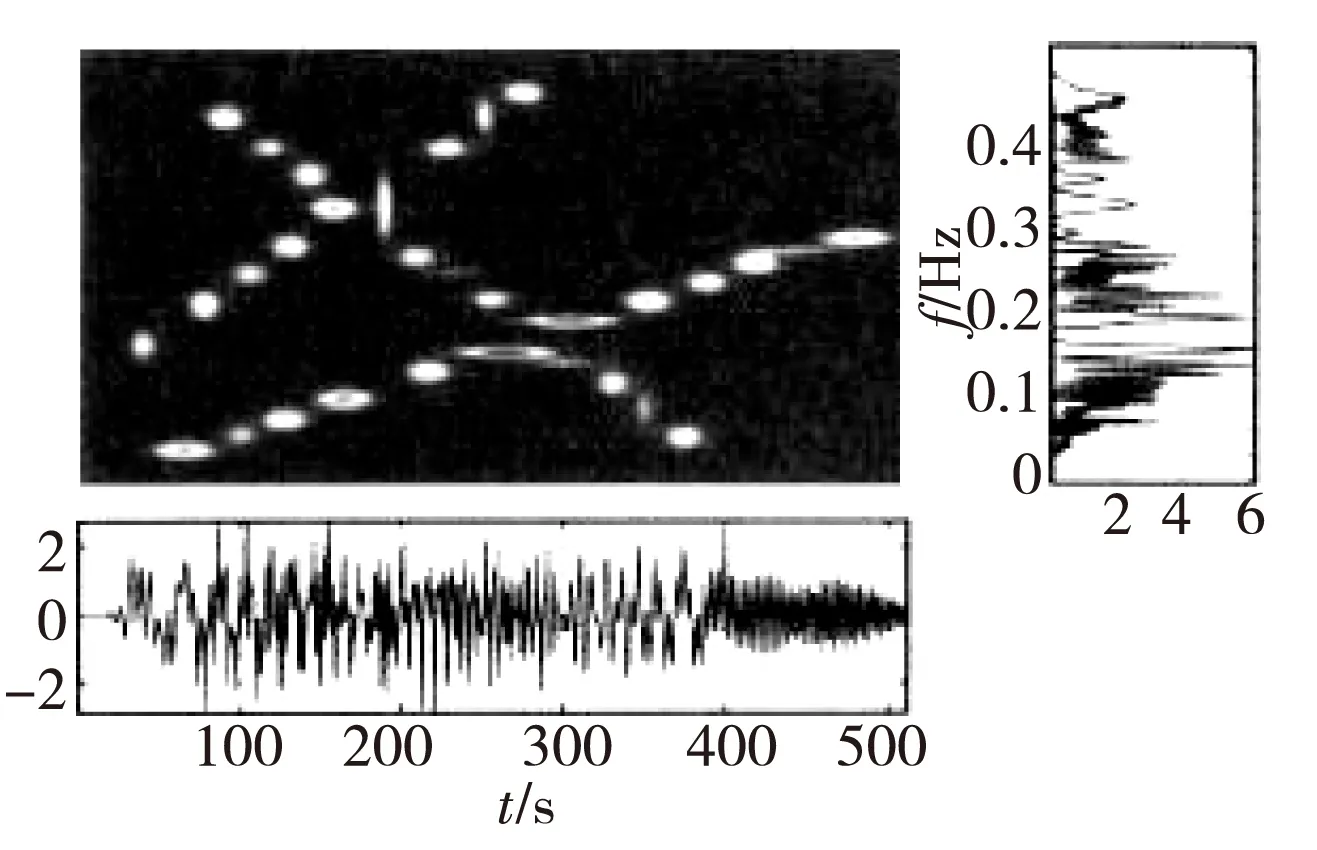
图2 三分量线调信号分解的Gabor原子时频图Fig.2 Gabor atom time-frequency picture of three LFMs
2.2 算法步骤
基于凸优化基追踪算法进行参数估计,最重要的环节是求解出稀疏向量x。后续对调频斜率、起止频率的估计以及信号的稀疏重构都是围绕稀疏向量x展开。
步骤1:求解稀疏向量x。利用CVX工具箱求解问题的SOCP形式。在此处理过程中,设置适当门限,挑选稀疏向量x。
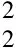
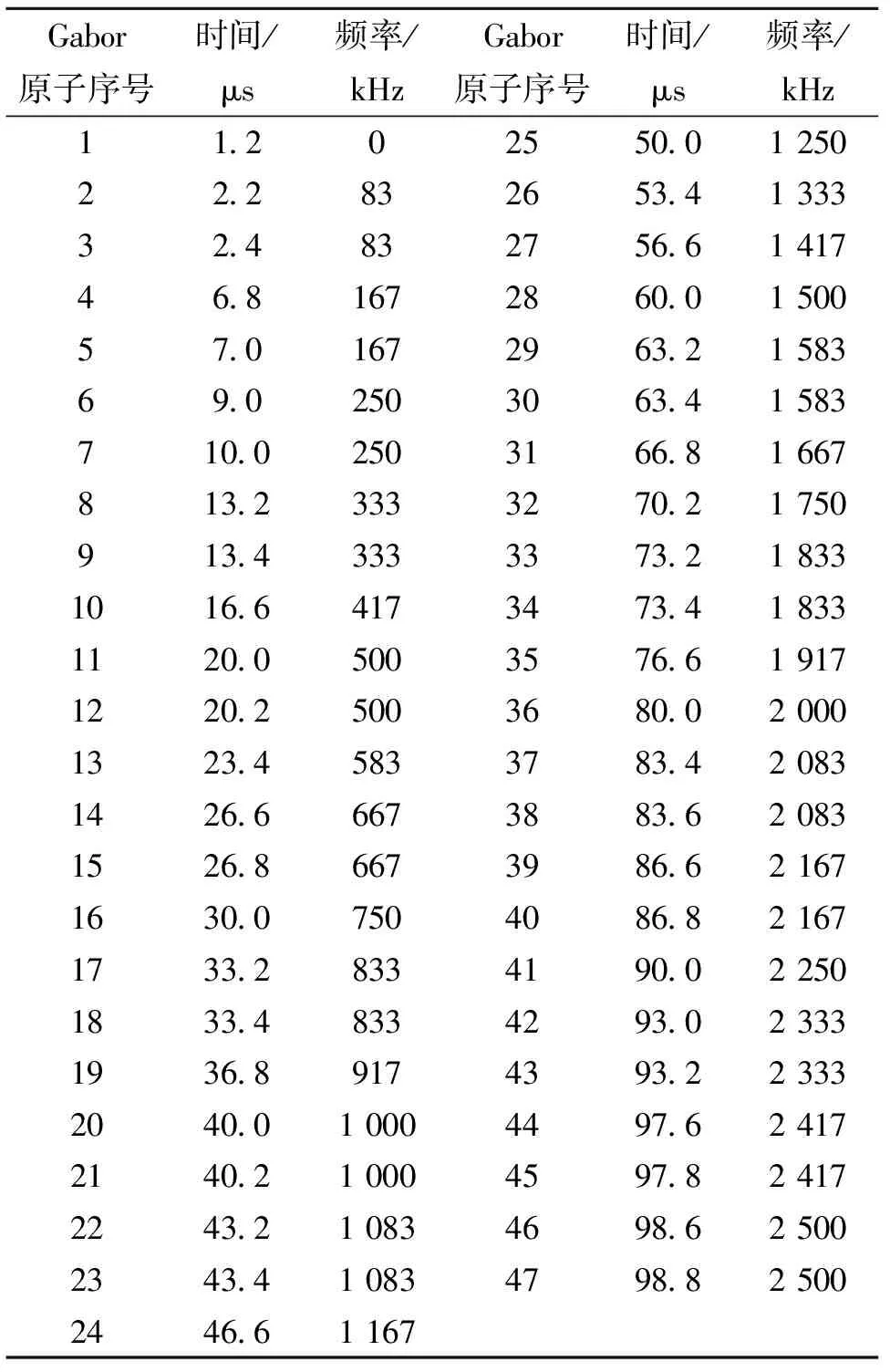
步骤3:调频斜率估计。提取A2中包含的Gabor原子的参数(τi,wi)做时频图。观察得,各原子所在点的排布呈一条直线状。用最小二乘线性估计得直线的斜率即为调频斜率。
步骤4:起止频率估计。在时频图中,挑选出中心时间最大最小的点,对起始终止频率进行估计。
3 仿真实验
取信号幅度a0=1,初始频率f0=0 MHz,脉冲宽度PW=100 μs,脉内调制带宽B=2.5 MHz,脉冲调制斜率μ0=2.5×1 010 Hz/s,采样频率fs=5 MHz。噪声w(t)为加性高斯白噪声。
实验1 有效性分析
当观测样本数N=501,信噪比20 dB时,任意取其中一次试验,所得稀疏原子序号及对应的Gabor原子信息分别如图3与表1。

图3 稀疏原子筛选Fig.3 Screening of sparse atoms
Gabor原子序号时间/μs频率/kHzGabor原子序号时间/μs频率/kHz1120255001250222832653413333248327566141746816728600150057016729632158369025030634158371002503166816678132333327021750913433333732183310166417347341833112005003576619171220250036800200013234583378342083142666673883620831526866739866216716300750408682167173328334190022501833483342930233319368917439322333204001000449762417214021000459782417224321083469862500234341083479882500244661167
从图3看出,此时设置门限为0.05,直线即为门限。筛选出的47个原子幅度远远比其余原子大,具有代表性。所得原子序号求得对应的Gabor原子,其信息如表1。
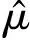
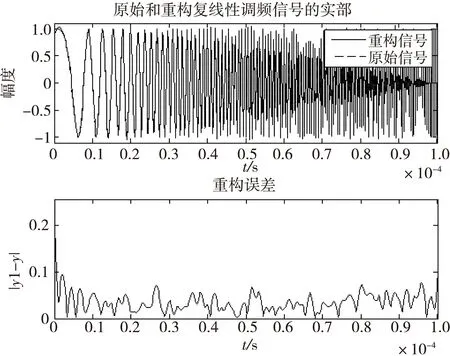
图4 原信号实部重构Fig.4 Estimation of LFM coefficient

图5 线性调频斜率估计Fig.5 Estimation of LFM coefficient
实验2 参数估计性能分析
其他条件不变,信噪比从0 dB到24 dB间隔4 dB取值,蒙特卡洛仿真100次,调频斜率估计情况如图6。由图6可知,针对调频斜率的估计,与文献[2]FrFT方法相比,在信噪比6 dB左右,两者估计效果相当,此时RMSE为7.4×107,相对误差为0.296%。随着信噪比不断提高,本文方法曲线较FRFT方法下降更多,更贴近CRB,斜率估计精度更好。
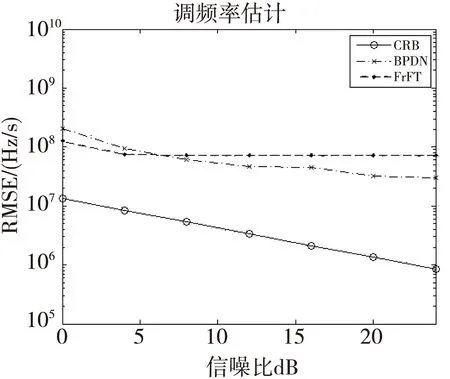
图6 调频斜率估计Fig.6 Estimation of LFM coefficient
从图5与图7、图8三幅图中可知,随着信噪比降低,挑选出的Gabor原子逐渐被噪声所淹没,数量不断减少,对调频斜率的估计影响相对较小,但对起始与终止频率的估计造成了比较大的影响。在信噪比小于0 dB时,Gabor原子几乎全部被噪声淹没,使得斜率无法估计。除了信噪比对起止频率估计影响外,当频率划分点k较大时,估计效果较好,然而大大增加了字典A的大小与计算复杂度。故该方法对起止频率的估计仅限于理论分析与信噪比较大时的估计。
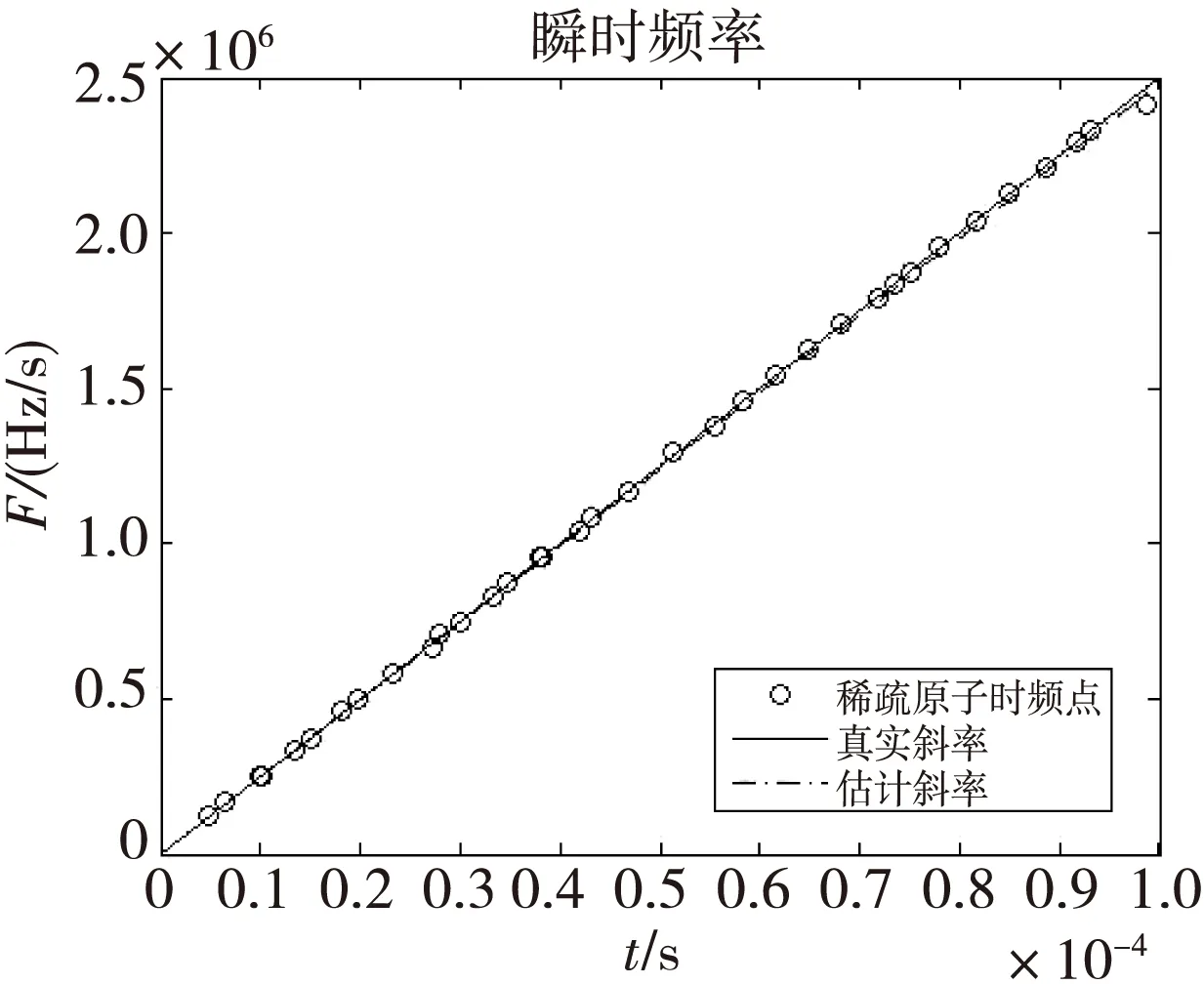
图7 信噪比10 dB时瞬时频率图Fig.7 Instantaneous frequency while SNR=10 dB
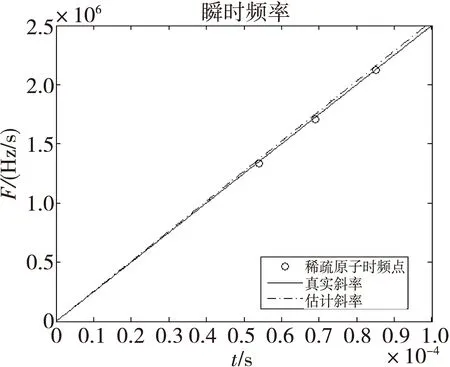
图8 信噪比-1 dB时瞬时频率图Fig.8 Instantaneous frequency while SNR=-1 dB
4 结论
本文提出基于凸优化基追踪算法的线性调频信号参数估计方法。该方法利用Gabor字典良好的时频特性,以l1范数稀疏正则最小二乘模型为目标函数求解稀疏Gabor原子,并推导了问题的SOCP形式。最后通过提取的Gabor原子中所含信息对信号进行参数估计。仿真分析表明:原始信号在过完备Gabor字典上展开,求解原子的稀疏性好,对原信号重构精度高;在较高信噪比环境下,该方法对斜率与初始、终止频率等参数估计效果较好,是一种有效的参数估计方法。
[1]张容权, 杜雨洺, 杨建宇, 等. 一种LFM信号最大似然估计模型与参数估计快速算法[J]. 电波科学学报,2005,20(5):651-655
[2]袁振涛,胡卫东,郁文贤,等. 用FrFT插值实现LFM信号的参数估计[J]. 信号处理,2009,25(11):1727-1731.
[3]齐林, 陶然. 基于分数阶Fourier变换的多分量LFM信号的检测和参数估计[J]. 中国科学E辑:技术科学,2003,33(8):749-759.
[4]Stephen Boyd, Lieven Vandenberghe. Convex Optimization[M]. New York: Cambridge University Press, 2013.
[5]Mallat S G, Zhang Z F. Matching pursuit with time-frequency dictionaries[J]. IEEE Trans. on Signal Processing, 1993, 41 (12) :3397- 3415.
[6]闫浩,董春曦,赵国庆,等. 基于压缩感知的线性调频信号参数估计[J]. 电波科学学报, 2015,30(3):449-454.
[7]Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. Ieee Transactions on Information Theory, 2007, 53: 4655-4666.
[8]王康, 叶伟, 劳国超, 等. 一种基于压缩感知的宽带SAR信号侦察方法[J]. 理论与方法, 2014, 33(4):40-43.
LFM Signal Parameter Estimation Based on Convex Optimization Basis Pursuit
XIA Jie, ZHOU Qingsong, ZHANG Jianyun, DONG Wei
(Electronic Engineering Institute of PLA, Hefei 230037, China)
In order to improve traditional parameter estimation accuracy of wideband LFM signal, a method of parameter estimation of LFM signal based on Convex optimization basis pursuit was presented. The method utilized good time-frequency characteristics of Gabor atoms and usedl1norm Sparse regular least squares model to solve and estimate parameter. Simulation results showed that the proposed method had sparse nature of atoms, high precise reconstruction and good parameter estimation.
convex optimization basis pursuit; linear frequency modulation signal; time-frequency analysis; parameter estimation
2016-07-01
国家自然科学基金项目资助(11375263)
夏杰(1991-),男,浙江宁波人,硕士研究生,研究方向:宽带雷达信号侦察与干扰。E-mail:jojo565294464@sina.com。
TN911
A
1008-1194(2016)06-0084-05
