砾岩球度对砾岩地层电阻率影响的数值模拟研究

2017-01-14屈雄伟李彬

计算机时代 2016年12期

屈雄伟+李彬

摘要：地层电阻率是石油测井油气解释评价的重要参数，随着油气精细勘探的深入，砾岩地层等具有各向异性的储集层逐渐成为重要的勘探方向。利用COMSOL有限元软件绘制单个砾岩地层模型，在恒定电流场下根据电流连续性定理求得砾岩地层使视电阻率。通过COMSOL有限元软件数值计算得出改变砾岩球度对砾岩地层电阻率有一定的影响，确定球度的砾岩对应于不同背景地层影响程度也不同。在此研究基础上得到球度的影响机理，为实际复杂储集层的测井油气评价和解释提供理论依据。

关键词：砾岩地层；球度；电阻率； COMSOL

中图分类号：P319.2 文献标志码：A 文章编号：1006-8228（2016）12-28-04

Abstract： Formation resistivity is an important parameter in evaluation of oil well logging and interpretation of oil and gas， stratum which has anisotropic reservoir such as conglomerate stratum gradually become important exploration direction， with the deepening of the fine oil and gas exploration. This paper uses the finite element software COMSOL to draw a single conglomerate stratum model， and the apparent resistivity of the conglomerate stratum is determined by the current continuity theorem under constant current field. The change of conglomerate sphericity has certain influence on the resistivity of conglomerate formation according to the calculation of COMSOL finite element software， and it is determined that conglomerate of certain sphericity has different influence on different background formation. The influence mechanism of sphericity is obtained based on this study， which provides theoretical basis for the evaluation and interpretation of oil and gas logging in complex reservoirs.

Key words： conglomerate formation； sphericity； resistivity； COMSOL

0 引言

地层电阻率是石油测井油气解释评价的重要参数，随着油气精细勘探的深入，砾岩地层等明显电各向异性的储集层成为重要的勘探方向。球度是用来定量描述一个颗粒近似于球体程度的参数，球度的计算方法也有许多种，根据Quiroga和Fowler[1]的定义，球度描述的是颗粒在三个轴方向（X、Y、Z轴）长度的近似程度。比如Waddell[2]提出了外接最小球度法，即颗粒体积与颗粒外接最小球的体积之比的立方根的大小来表示。Krumbein[3]在Waddell定义球度方法的基础上，将颗粒等效为具有相同体积的球体和椭球体，提出了两种新的球度定义的方法。斯尼德和福克（S.Need and Folk）[4]在评论了过去测量球体的方法后提出了最大投影球度法，用以确定球度参数数值。它是用与颗粒体积相同的球体的横切面积与该颗粒的最大投影面积的比值的立方根求得的。

实际应用证明，最大投影球度法比其他方法更有利于研究颗粒在流体介质中的状态。颗粒的三个轴越接近相等，其球度越高；相反，片状和柱状颗粒都具有很低的球度。李北星等[5]运用图像分析软件测定了石灰石和铁尾矿废石粗骨料的三轴特征、圆度和球度，并对不同粒级粗骨料的等轴率、圆度和球度进行了统计性分析。裴润有等人[6]提出了一种基于计算机图像处理的压裂支撑剂圆度和球度测量方法，提高了测定效率。本文通过COMSOL软件数值计算研究砾岩地层中砾石球度对地层电阻率的影响，对于了解地层信息有着重要的意义。

1 砾岩模型构建

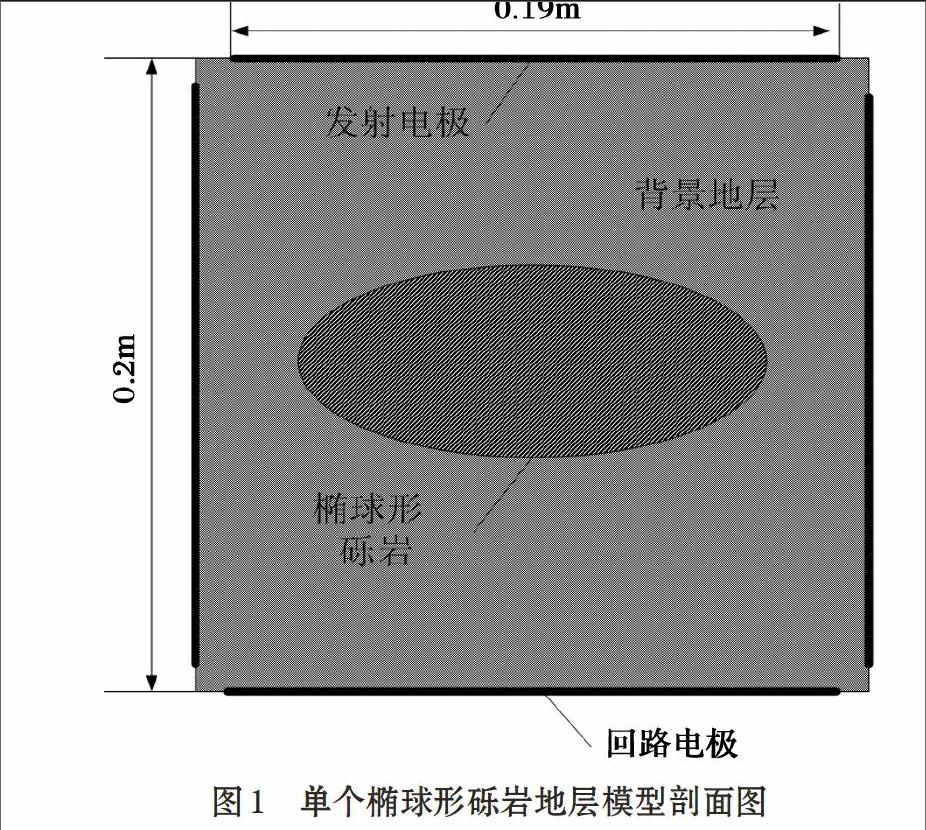
砾岩主要由砾石和基质组成，砾岩地层的构造非常复杂。图1为砾岩地层模型的剖面图，图的中间为椭球形砾岩，外面为基质。砾岩地层模型棱长0.2m，电极长度0.19m。

砾岩球度用S表示，计算公式为：

⑴

⑵

其中，R为与椭球形砾岩颗粒体积相同的球体半径， A、B为该颗粒的最大投影面的半轴长度。在图1模型中，对发射和接收回路施加恒定电压，测量流过模型的电流从而确定砾岩地层在各个方向的电阻率。

由普通物理学得知，均匀材料制成的形状规则的导体，若导体两端电压差为ΔU，通过的电流为I，则导体的电阻率R定义为[7]：

⑶

其中，S为导体的横截面积，L为导体的长度。电阻率的单位是欧姆米（Ω·m）。

一般L和S均取固定值，令，则有：

⑷

⑸

其中，K为电极系系数，其值仅与模型中所加的电极几何尺寸有关。在上述模型中令砾岩电阻率和背景电阻率均为1Ω·m，发射端接1V电压，回路端接地（R=1Ω·m，ΔU=1V），则有：

⑹

⑺

当砾岩电阻率与背景电阻率不同时即地层不是均匀的时候，将仪器常数K带入式⑸，即可得出地层电阻率。

上述公式中的电流I，根据电流连续性定理，对发射端或回路端的法向电流密度进行面积分可得，电流由式⑻求得：

⑻

本文在此基础上研究砾岩球度以及不同球度的砾岩的位置对砾岩地层视电阻率的影响。

2 砾岩球度对砾岩地层电阻率的影响

计算砾岩地层电阻率的基本思想是：在砾岩地层模型岩坐标轴方向添加有一定电压差的发射电极和回路电极，测量流过回路电极的电流值，从而求得砾岩地层电阻率值。模型中设定砾岩体积占砾岩地层体积的20%，当砾岩为规则的圆球状时半径约为0.073m，此时砾岩球度最大。根据砾岩球度的定义公式⑵，当砾岩在Z轴方向半轴C越小，其在X-Y平面的投影面积越大而球度越小，本文选择球度的范围是0.81～1。在模型的侧面添加棱长为0.19m的铜板电极，设定发射电极和回路电极的电势差为1V。对模型进行数值求解，求得不同方向上的K值。在图1模型中设定砾岩为扁平状的球体（A=B），均匀地层的情况下K值的数值计算结果为

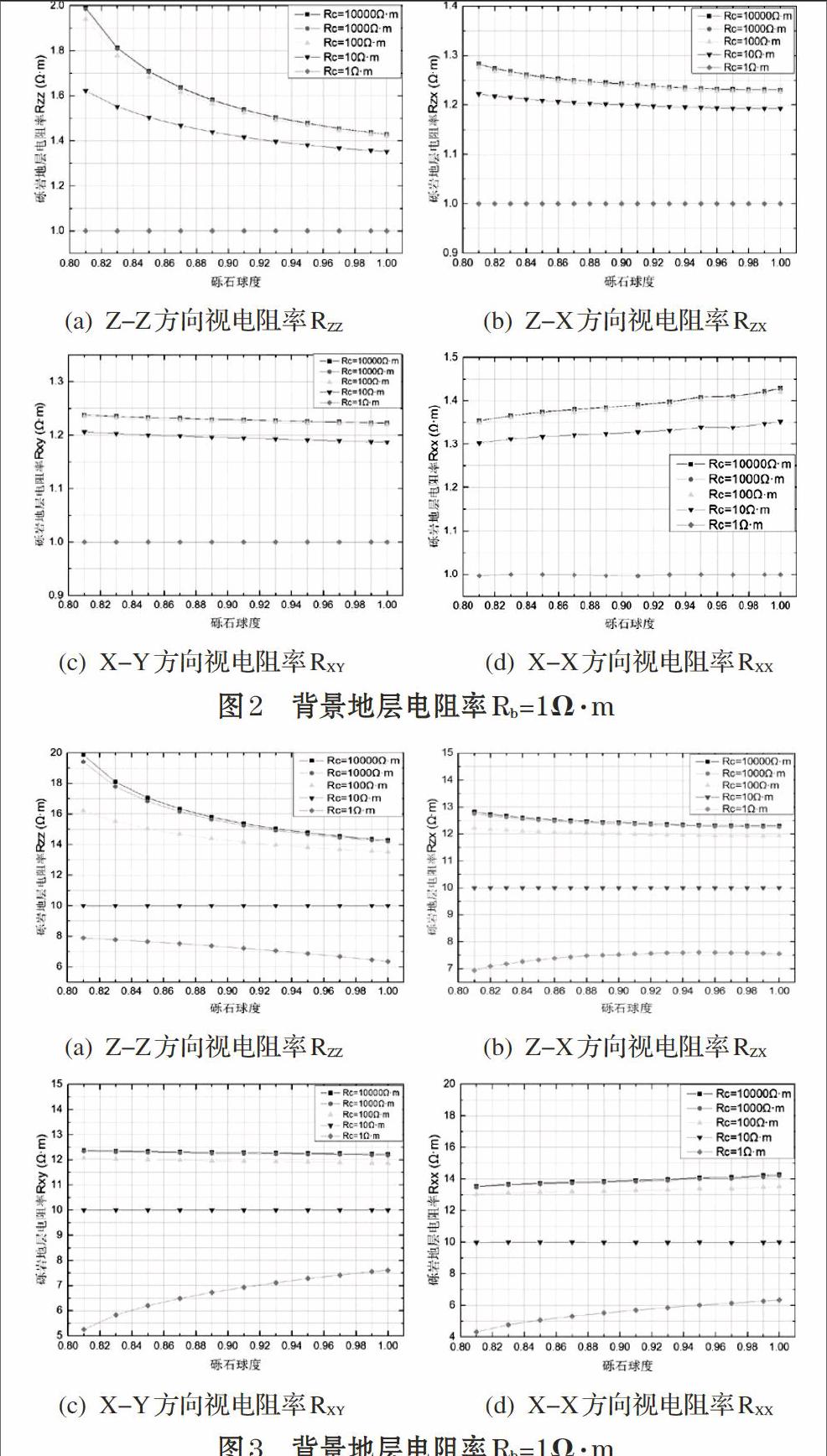
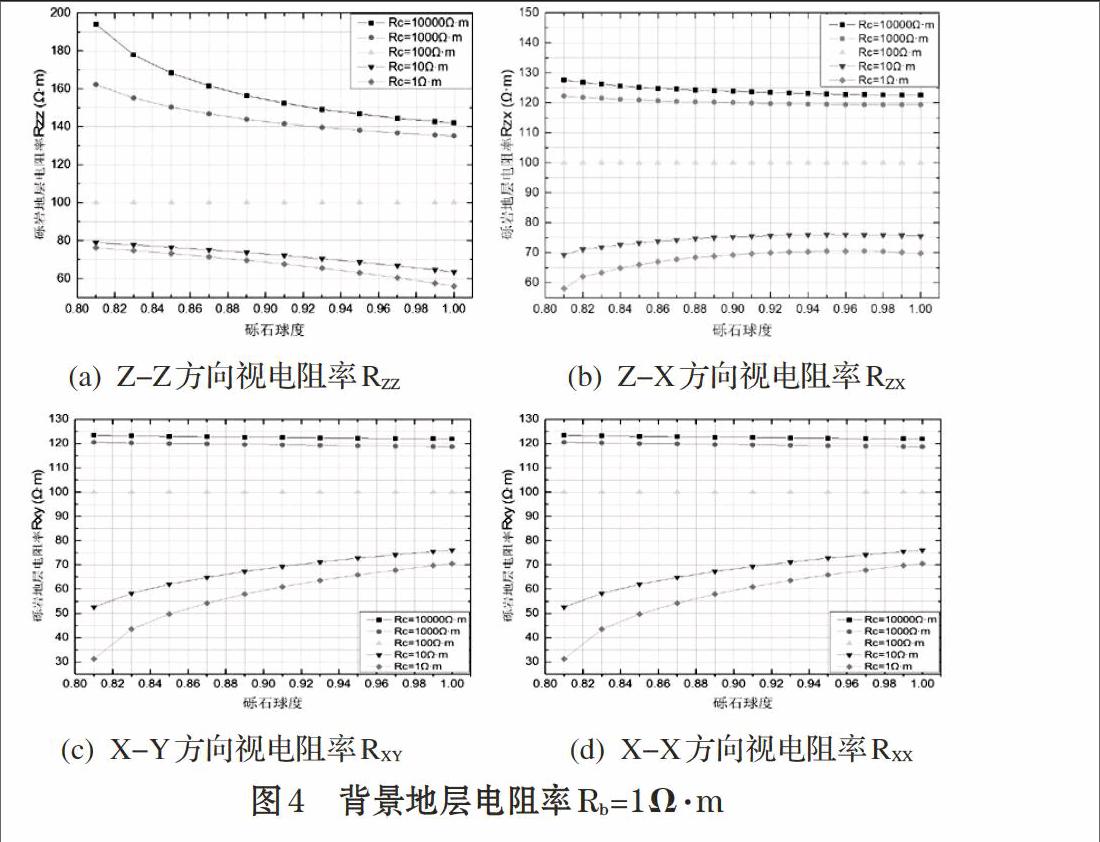
对图2、图3和图4对比分析，得出以下结论。

⑴ 背景电阻率Rb为1Ω·m、10Ω·m和100Ω·m，砾岩电阻率大于背景地层电阻率时，砾岩地层视电阻率RZZ、RZX和RXY随着砾岩球度的增大而减小；砾岩地层视电阻率RXX随球度的增大而增大。

⑵ 背景电阻率Rb为10Ω·m、100Ω·m，砾岩电阻率小于背景地层电阻率时，砾岩地层视电阻率RZZ随着砾岩球度的增大而减小；砾岩地层视电阻率RZX、RXY、RXY随着砾岩球度的增大而增大。

⑶ 当砾岩电阻率值（RC=10000Ω·m和RC=1000Ω·m）远大于背景地层电阻率（Rb=1Ω·m）时，测量得到的砾岩地层电阻率的值几乎相等。

⑷ 相同球度对应的砾岩地层视电阻率RZZ的值大于RZX、RXY和RXX。RZX在球度较小时大于RXY，随着球度的增大，RZX和RXY接近相等，因为球度较小的时候砾岩为扁球状，砾岩在X-Y方向的投影比Z-X方向的投影小，电流更容易到达回路电极，随着球度的增大砾岩越接近于圆球，砾岩在X-Y方向的投影和Z-X方向的投影接近相等。

3 影响电阻率变化的机理分析

图5为椭球形砾岩球度为0.85，砾岩的电阻率为RC=10000Ω·m，背景地层电阻率取Rb=1Ω·m时，单个砾岩地层模型在静电场下各个方向的截面图。图中背景颜色为电位分布图，白色为电流线，垂直于电流线的线条是电位的等势线。从图5中电流线流动轨迹可以看出，砾岩电阻率远大于背景地层电阻率时，电流线从发射电极出发绕过砾岩到达回路电极。

图6为砾岩电阻率为1Ω·m，背景电阻率为100Ω·m，砾岩球度S=0.85时，砾岩各个方向的电流线图。通过图6中电流线的流动轨迹可以看出，，当砾岩电阻率小于背景电阻率时，电流更加容易通过砾岩，电流线从发射电极出发穿过砾岩到达回路电极。

4 结束语

本文基于COMSOL软件有限元仿真软件，在恒定电流场下，研究了单个砾岩地层模型中砾岩球度对整个地层电阻率的影响。研究表明砾岩地层电阻率RZZ随着砾岩球度的增大而减小，砾岩球度越大其投影面积越小，电流越容易穿过地层到达回路电极。砾岩地层电阻率RZX，RXY在砾岩电阻率大于背景地层电阻率时，随着砾岩球度的增大变化很小，在砾岩电阻率小于背景电阻率时，随着砾岩球度的增大而增大。

参考文献（References）：

[1] QUIROGA P. N，FOWLER D. W. The Effects of aggregates

characteristics on the performance of portland cement concrete[A]. Research Report： ICAR 104-1F International Center for Aggregates Research，2003.

[2] WADELL H. Volume， Shape， and Roundness of Rock

Particles[J]. Journal of Geology，1932.40：443-451

[3] Krumbein W C. Measure and geological significance of

shape and roundness of sedimentary particles[J].Journal of Sedimentary Petrology，1941：64-72

[4] 赵澄林、朱筱敏主编.沉积岩石学[M].北京：石油工业出版社，

2008.

[5] 李北星，王威，陈梦义，叶茂.粗骨料的等轴率、圆度和球度及

其相互关系[J].建筑材料学报，2015.18（9204）：531-536

[6] 裴润有，解彩丽，胡科先，吕新荣.压裂支撑剂圆度球度测定方