基于UKF的自适应野值剔除算法
2017-01-13马姓
马 姓
(合肥工业大学电气与自动化学院,合肥 230009)
基于UKF的自适应野值剔除算法
马 姓
(合肥工业大学电气与自动化学院,合肥 230009)
UKF(Unscented Kalman Filter,UKF)算法被广泛应用于运动目标跟踪中,取得了很好地跟踪效果;但是在实际应用中,由于各种随机因素的影响,使得观测数据中不可避免地含有干扰数据,而这些干扰数据的存在使得UKF算法跟踪精度不断地下降,甚至会使滤波发散;针对这一问题,提出一种基于UKF的自适应野值剔除算法,根据信息对动态观测数据中的干扰数据进行实时检测,当检测到干扰数据时,通过修正预测值和增益来提高跟踪精度;通过与UKF算法实验仿真对比,结果表明改进UKF算法可以有效地抑制了干扰数据对滤波的影响,能够很好地对运动目标进行跟踪,并且跟踪精度较高。
野值;信息;滤波发散;无迹卡尔曼滤波
1 基于UKF的自适应目标跟踪算法
1.1 算法的提出
非线性离散系统,无迹卡尔曼滤波[10]的动态方程为:

其中:xk为系统状态,zk为系统的测量值,f为状态转移函数,h为观测函数,wk为过程噪声,均值为零、方差为Qk的高斯白噪声;vk为观测噪声,均值为零、方差为Rk的高斯白噪声。
算法主要基本步骤为:
1)初始化:

2)假设输入状态x为n维向量,选取2n+1个sigma采样点并计算相对应的权值:

3)采样点的一步预测:

4)状态的一步预测:

综上可知,式(2)~(13)是UKF算法的整个滤波过程。
由于外界环境中各种存在随机噪声干扰,使得观测数据中存在着干扰数据,这些干扰数据会不同程度的影响UKF滤波过程,甚至会使滤波发散。由公式(12)分析可知,预测值、增益和观测数据是影响UKF滤波器的输出精度的主要因素,为了改善UKF滤波器的输出精度,在UKF算法的基础上对其预测值和增益进行修正。
13)信息:

式(14)中,vk+1为k+1时刻的信息,反映了观测值与预测值之间的偏差。
14)信息的方差:

检测观测数据中是否有干扰数据,检测公式为:
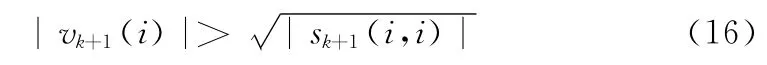
式(16)中vk+1(i)表示信息向量vk+1的第i个分量,sk+1( i,i)表示矩阵sk+1对角线上的第i个元素。
当信息满足公式(16)时,则认为当前的观测数据是干扰数据,应修正当前k+1时刻的UKF增益Kk+1,修正公式为:

式(17)中,Kk+1(i,i)表示矩阵Kk+1对角线上的第i个元素。
当信息不满足公式(17)时,则认为当前的观测数据是正常的,但是如果信息满足公式(18):


至此,式(2)~(19)是改进UKF算法的整个滤波过程。
1.2 修正原理
以观测值为圆的中心,以观测误差的最大值为半径R画一个圆,记为量测圆。仍以观测值为圆的中心,以βi倍的以观测误差的最大值为半径r画一个圆,记为预测圆。如图1所示。
当|vk+1(i)|>R时,则认为当前的观测数据是干扰数据,系统的误差主要来自于观测值,则应降低当前时刻的卡尔曼增益,减少观测值对系统的状态估计占有的权重,增加预测值对系统的状态估计占有的权重。由式(17)重新计算k+1时刻的卡尔曼增益Kk+1。
当r<|vk+1(i)|≤R时,则认为当前的观测数据是正常的,系统的误差主要来自于预测值,则应修正预测值。由式(19)重新计算k+1时刻的预测值^xk+1|k。
当|vk+1(i)|≤r时,认为观测数据和预测值都是正常的,不做任何修正。
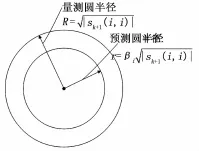
图1 修正原理图
2 仿真实验
本文是基于RSSI信号的位置指纹室内定位系统,实验仿真区域为12 m×10.5 m。为了使系统定位的轨迹更加的接近运动目标的实际运动轨迹,需要对系统定位算法获取到的运动目标的位置信息进行滤波处理。使用系统定位算法获取到的位置信息作为改进前后UKF滤波算法的观测数据,通过matlab进行实验仿真,使用改进前后的UKF滤波算法对X轴方向的位置信息进行滤波,仿真结果如图2和图3所示。
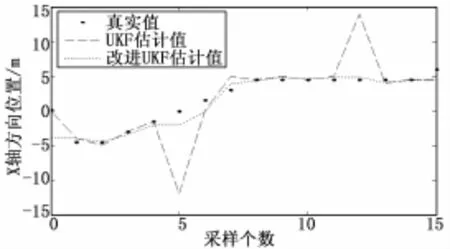
图2 改进前后UKF的位置估计

图3 改进前后UKF的位置估计误差
仿真结果分析,从图2和图3的曲线可知,当X轴方向的位置信息在第5次和第12次为干扰数据时,UKF算法的估计曲线与运动的实际轨迹偏差较大,且估计误差也较大。而改进UKF算法的状态估计曲线与运动的实际轨迹很接近,且估计误差比较小。以上分析表明,当观测数据中存在干扰数据时,改进UKF算法可以有效地抑制了干扰数据对滤波的影响,能够很好地对运动目标进行跟踪,并且跟踪精度较高。
3 结论
在实际目标跟踪应用中,由于各种随机因素的影响,使得观测数据不可避免地含有干扰数据,传统的UKF滤波算法抗干扰能力较弱,干扰数据的存在使得滤波精度下降,甚至会使滤波发散。针对这一问题,本文对UKF滤波算法进行了深入的研究,提出一种改进的UKF滤波算法,根据信息来检测是否存在干扰数据,当检测到干扰数据时,通过修正其预测值和增益来提高滤波精度。实验仿真结果表明,当出现干扰数据时,改进的UKF滤波算法可以有效地抑制干扰数据对滤波的影响,能够很好地对运动目标进行跟踪,并且跟踪精度较高。
[1]许建波.基于WLAN位置指纹的室内定位技术研究与实现[D].北京:北京工业大学,2014.
[2]Cortina E,Argentina BA,Otero D,et al.Maneuvering target tracking using extended Kalamn Filter[J].IEEE Trans.On Aerospace Electronic Systems,1991,27(1):155-158.
[3]郝晓静,李国新,李明珠,等.无迹卡尔曼滤波算法在目标跟踪中的研究[J].电子设计工程,2012,20(13):54-57.
[4]Gustafsson F,Gunnarsson F,Bergman N,et al.Particle filters for positioning,navigation and tracking[J].IEEETransactions on signal processing,2002,50(2):425-437.
[5]夏天维,候 翔.基于自适应Kalman滤波的机器人运动目标跟踪算法[J].计算机测与控制,2015,23(1):173-175.
[6]Liu C Y,Shui P L,Li S.Unscented extended Kalman filter for target tracking[J].Journal of Systems Engineering and Electronics,2011,22(2):188-192.
[7]陈 松.基于粒子滤波的自适应机动目标跟踪[D].昆明:昆明理工大学,2014.
[8]郝顺义,刘华伟,黄 国,等.基于梯度自适应规则的自适应UKF算法及其应 [J].计算机测量与控制,2014,22(4):1205-1208.
[9]杨永建,樊晓光,王晟达,等.基于修正卡尔曼滤波的目标跟踪[J].系统工程与电子技术,2014,36(5):847-851.
[10]Julier S,Uhlmann J,Durrant WH F.A new method for the nonlinear transformation of means and covariances in filters and estimators[J].IEEE Transactions on Automatic Control,2000,45 (3):477-482.
Adaptive Outlier Eliminating Algorithm based on UKF
Ma Xing
(School of Electric Engineering and Automation,Hefei University of Technology,Hefei 230009,China)
UKF algorithm is widely used in moving target tracking,the effect of target tracking is very good.But in practical application,due to the influence of all kinds of random factors,which makes some interference data inevitably contained in the observation data.The existence of interference data leads to a constant decline in tracking precision,and even makes filtering divergence.In order to solve this problem,an adaptive outlier eliminating algorithm based on UKF algorithm is given,which can real-timely detect interference data in the dynamic observation data according to the innovation.When interference data is detected,prediction and gain will be amended to improve tracking accuracy.Compared with UKF algorithm,the results of experiment simulation show that the improved UKF algorithm can effectively suppress the influence of interference data in filtering,the effect of target tracking is very good,and tracking precision is higher.
outlier;innovation;filter divergence;unscented Kalman filter
1671-4598(2016)08-0283-03
10.16526/j.cnki.11-4762/tp.2016.08.077
:TP393
:A
0 引言
2016-03-03;
:2016-04-13。
马 姓(1989-),女,安徽凤阳人,硕士研究生,主要从事复杂系统建模与控制方向的研究。
在基于RSSI(received signal strength indication)信号的定位系统中,对运动目标进行跟踪常用的方法有:卡尔曼滤波[1]、扩展卡尔曼滤波[2]、无迹卡尔曼滤波[3]和粒子滤波[4]等。由于环境中存在各种随机噪声干扰,使得观测数据不可避免地受到噪声的污染,导致观测数据中存在着干扰数据,这些干扰数据会不同程度的影响滤波器的滤波过程,甚至会使滤波发散。为了解决这类问题,在文献[5]中提出一种自适应卡尔曼滤波目标跟踪算法,对于线性系统具有很好的跟踪效果,但是对于非线性系统跟误差较大。在文献[6]中提出一种改进的扩展卡尔曼滤波目标跟踪算法,弱非线性系统具有很好的跟踪效果,但是对于强非线性系统跟误差较大。在文献[7]中提出了一种自适应粒子滤波目标跟踪算法,但是该方法在粒子迭代的过程中存在粒子退化的问题。在文献[8]中提出一种基于梯度自适应规则的UKF算法,但是该方法的计算复杂度比较大。在文献[9]中提出一种根据信息来修正预测值的目标跟踪算法,取得很好的跟踪效果。在此基础上,本文提出一种基于UKF的自适应野值剔除算法,根据信息对其预测值和增益进行自适应控制。
