基于滚动粒子群算法的空对地攻击轨迹控制决策
2017-01-13雷鹏飞1魏贤智1高晓梅2汪志宏1
雷鹏飞1,魏贤智1,高晓梅2,汪志宏1
(1.空军工程大学航空航天工程学院,西安 710038;2.南京军区空军装备部,南京 210000)
基于滚动粒子群算法的空对地攻击轨迹控制决策
雷鹏飞1,魏贤智1,高晓梅2,汪志宏1
(1.空军工程大学航空航天工程学院,西安 710038;2.南京军区空军装备部,南京 210000)
针对空对地攻击的轨迹规划问题,建立战机的六自由度模型、全向RCS模型、以及各类威胁模型;选取推力系数、攻角以及横滚角为控制量,确立对地攻击航迹控制决策指标函数以及决策最优控制模型;采用滚动粒子群算法,通过粒子群算法获得控制量在每个决策时域内的最优值并结合滚动时域控制实现对航迹的在线规划;经过仿真分析表明该方法可以控制载机完成作战任务并能给出控制量的变化规律,为飞行员提供决策辅助信息。
对地攻击;轨迹控制;滚动粒子群算法;辅助决策
0 引言
在空地作战过程中,战场环境异常复杂,对飞行员带来极大的操纵压力。因此对战机进行轨迹控制时,仅仅规划出一条合适的航路是不够的,还需规划出随着作战过程的进行,飞行员所能操控的战机控制量变化规律,以此作为对战机攻击轨迹控制的辅助决策信息,减轻飞行员的操纵压力,提高作战效能。
针对轨迹控制决策问题,目前采取的方法有人工智能算法,诸如A*算法、粒子群算法(PSO)等主要用于对航迹的规划,传统的智能算法难以实现对航迹的实时控制也很难给出控制量的变化规律;Gauss伪谱法(GPM)[1]、勒让德伪谱法(LPM)[2]以及滚动伪谱法[3]等方法将航迹控制问题转化为连续系统最优控制问题并采用伪谱法将其转化为离散参数优化问题,求解在各个离散点处的最优控制量,再通过插值得到更多离散点处的最优控制量,当需要提高轨迹控制精度时,必须增加离散点数量,从而影响初值的设置以及算法的性能。
基于此,本文先将航迹规划时域进行离散,引入滚动时域控制(RHC)的思想,利用粒子群算法对各个离散时刻的战机控制量进行寻优,将得到的最优控制序列作用于系统从而解决了对地攻击轨迹控制决策问题。
1 基本模型的建立
1.1 战斗机六自由度模型的建立
1)战斗机运动学方程:
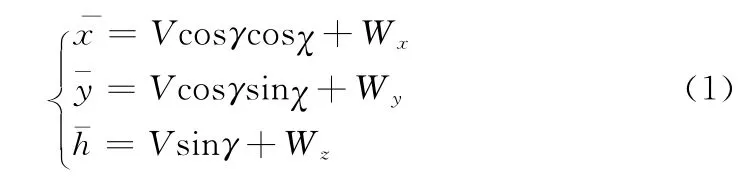
式(1)所示为在地理坐标系中战斗机的运动学方程,其中:(x,y,h)表示战斗机在空间中的位置;(Wx,Wy,Wz)表示飞机所在位置的风速在3个坐标轴方向上的分量;V表示飞机真空速;γ表示飞机航迹倾斜角;χ表示飞机航迹方位角。
2)战斗机动力学方程:
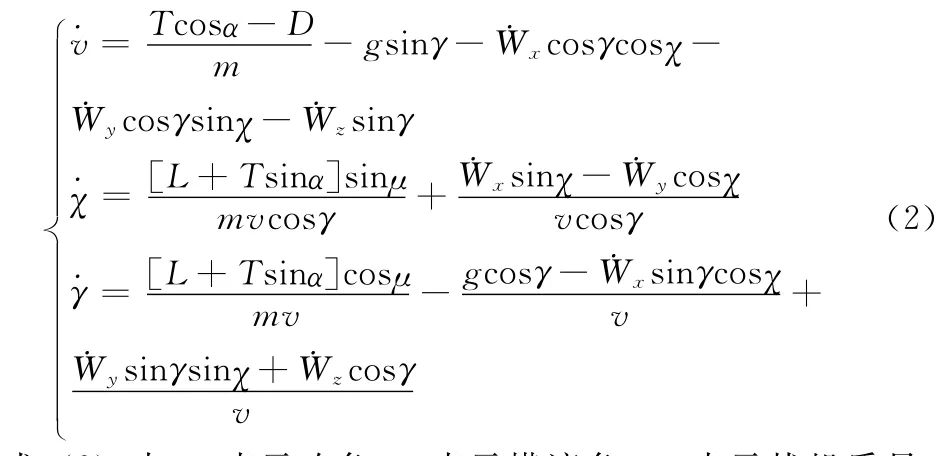
式(2)中,α表示攻角;μ表示横滚角;m表示战机质量;g为重力加速度;T表示发动机推力,其计算公式表示为:T=ηTmax,η为推力系数,Tmax为最大推力;阻力D=qSCD;升力L=qSCL;动压q=ρv2/2;S为战机机翼面积:CD、CL分别为升力和阻力系数;ρ为对应海拔高度上的空气密度计算方法如式(3):

为便于研究,本文采用某型战机的航空动力学参数信息,给出发动机推力与升力系数、阻力系数的计算模型如下:
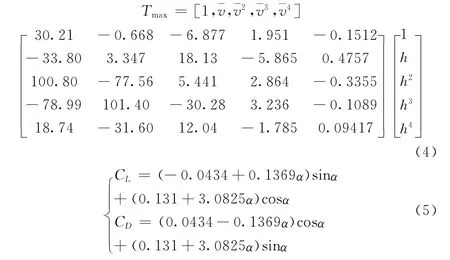
各变量之间的数值差异较大,对于提高决策算法的运算速度与精度带来了极大的不便,因此先将载机运动模型中各变量进行无量纲化处理,转化公式如下:
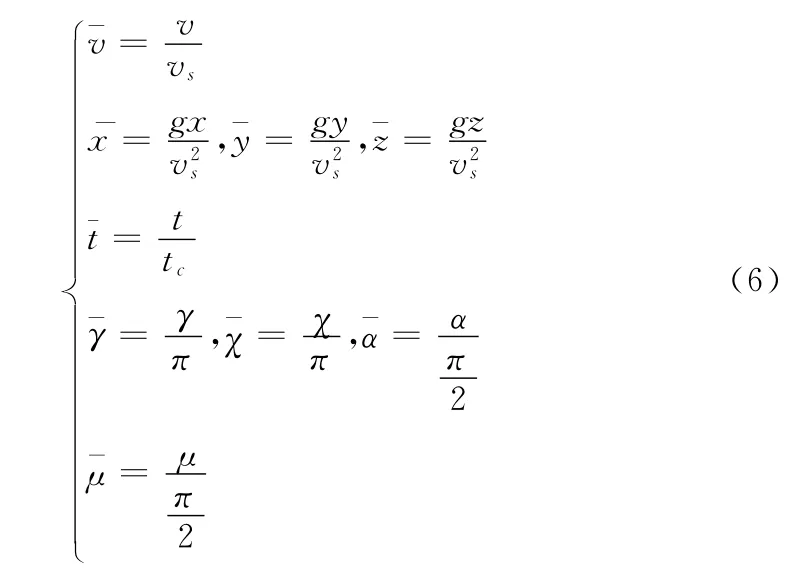
其中:vs表示音速;tc表示时间常量,其大小根据态势而定。
在此,利用式(6)对模型进行无量纲化处理,结果如下:

同时为了使生成的航迹切实可行,对各变量的取值范围作出规定:
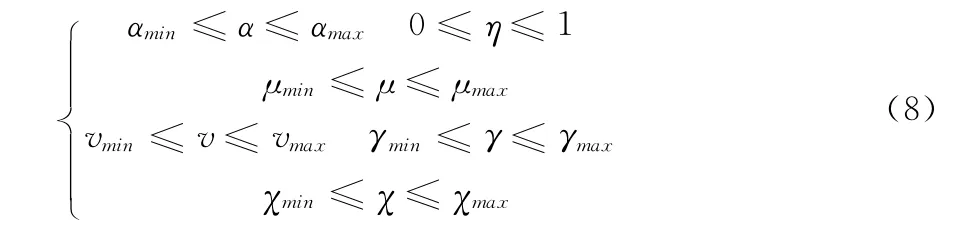
1.2 战机全向RCS模型建立
雷达散射截面积(RCS)是衡量战机隐身性能的关键指标,RCS越小,则战机被敌方威胁探测发现识别截获的概率也会随之降低,因此,通过技战术手段降低飞机的雷达散射截面积是各国各部队不断追求的目标。飞机相对于敌方雷达的姿态不同,其RCS也不相同,充分利用此特性就能达到战术隐身的目的,因此建立简化的战机全向RCS模型。
作战过程中,战机与探测雷达的性能参数已知,而战斗机的RCS与其相对于敌方雷达的方位角φ与俯仰角θ有关,相对态势如图1所示。
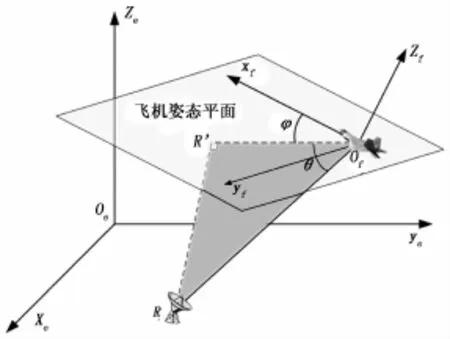
图1 战机与雷达相对态势
如图1所示,(Oxyz)e为地理坐标系;(Oxyz)f表示飞机坐标系;φ表示战斗机相对于雷达的方位角;θ表示战机相对于雷达的俯仰角。
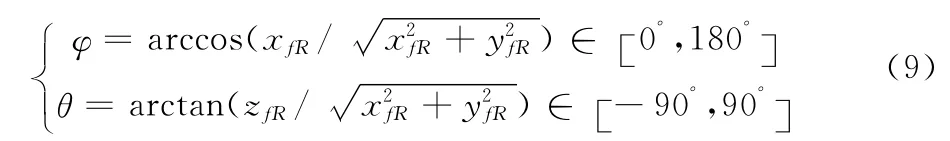
在不同的方位角与俯仰角条件下,战机的RCS计算方法[4]可简化为:
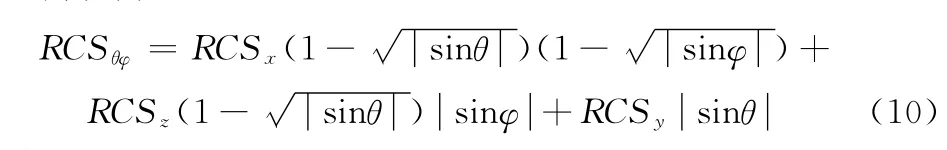
其中:RCSx表示飞机正视方向的RCS,RCSz表示飞机俯视方向的RCS,RCSy表示飞机侧视方向的RCS。
1.3 威胁建模
在威胁建模中我们主要考虑地形威胁、雷达探测威胁以及地形威胁和雷达探测威胁之间的相互作用。
1.3.1 地形威胁建模
相对于空战,对地攻击作战过程中,战机的飞行高度较低,一方面是突防作战的必然要求,另一方面通过低空飞行也能利用地形带来的雷达探测盲区降低战机被敌雷达探测截获的概率。因此,对地形威胁的研究十分有必要。
关于地形威胁空间的建立,本文采用带有经纬度以及高度信息的数字地图来反映实际地貌,通过经纬度与实际长度的转换关系,以及所选区域若大于一个经纬度所表示的范围时采用文献[5]中的数字地图拼接技术,可以实现地形威胁的建模如图2所示。
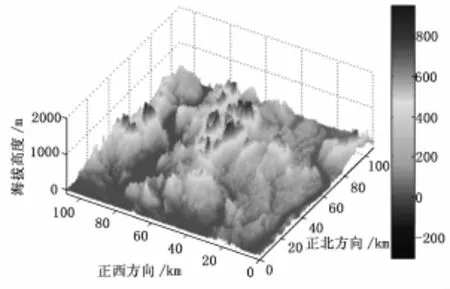
图2 地形威胁建模
战机在执行对地突防攻击任务时,为了避免碰地威胁,其飞行高度需要满足最小离地安全高度的限制,最小离地安全高度计算如下:

式中,(x,y,z)表示战机位置;h(x,y)表示对应坐标位置的地形高度;hmin表示最小离地安全高度,其大小与战机的姿态以及速度有关。
1.3.2 雷达探测威胁建模
将雷达探测威胁简化为一个以威胁源为球心,以探测距离为半径的半球形。地面雷达的探测距离可表示为:
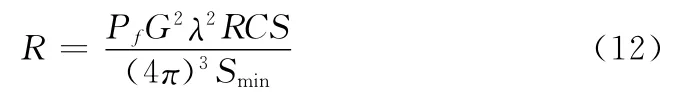
式中,Pf为地面警戒雷达的平均发射功率;G为警戒雷达的天线增益;λ为雷达波长;Smin表示雷达接收机所能接收的最小信号表示雷达接收机的灵敏度。
又根据前文分析得载机的RCS大小与其相对于探测威胁的姿态有关,故将雷达的探测距离简化为:
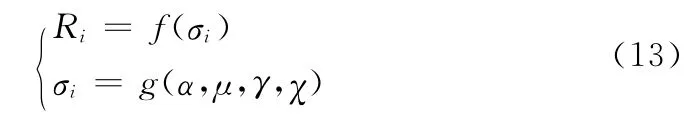
其中:Ri表示第i个威胁的作用距离;σi表示载机相对于威胁i的RCS值,与姿态有关。
1.3.3 雷达地形遮蔽建模
在突防作战中,除了利用上文所提到的战机全向RCS特性达到战术隐蔽攻击外,经常会利用地形遮蔽达到隐蔽突防的目的。因此,对雷达地形隐蔽作用的研究对于提高战机生存性能也具有重要意义[6]。
图3表示在某一方向角φ方向上,雷达信号由于受到山峰的影响,从而形成了雷达盲区。图中hR表示雷达高度;R表示雷达的最大探测范围,计算公式见上文地空导弹模型中探测雷达作用距离;θmax表示雷达射线与山顶交点对应的俯仰角;ρθ表示地形遮蔽点到雷达的水平距离。可以得到地形遮蔽条件下雷达的实际探测距离:
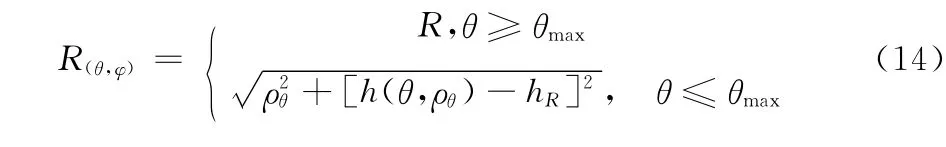

图3 地形遮蔽示意图
其中:h(θ,ρθ)表示雷达遮蔽点的高度。
假设战机位置坐标为(ρp,θp,φp),同时可以计算战机的突防安全高度如下:
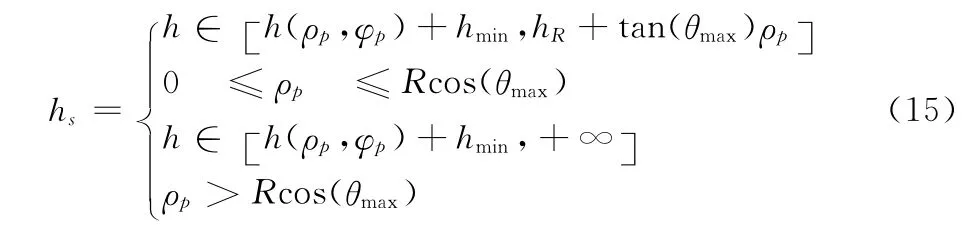
h(ρp,φp)为战机所处位置的地形高度;hmin为战机最小安全高度;hs为突防安全高度。
1.4 武器发射约束建模
进行航迹控制的目的是通过控制各个控制量以操纵载机的飞行状态,使其以最大的生存概率抵达所携带武器的投放区域并向目标投弹完成对目标的有效攻击,所以载机的姿态还需要满足相应武器的投放条件。约束模型如下:
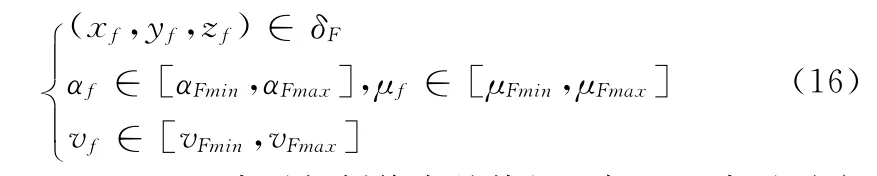
其中:(xf,yf,zf)表示规划终点处战机坐标;δF表示对应的武器可发射区;[αFmin,αFmax]、[μFmin,μFmax]、[vFmin,vFmax]表示规划终点处,载机攻角、横滚角和速度的允许范围。
2 航迹控制决策模型
2.1 决策指标函数的确立
本文利用粒子群算法并采用滚动时域控制的策略以期得到轨迹的实时控制决策,主要为获得各控制量随时间的变化关系,因此求导变量选择时间t;控制变量选取[αμη];状态变量取[xyzγχ]。
将航迹控制决策问题转化为最优控制问题需要建立一个能反映出作战任务需要的指标函数,表示如下:
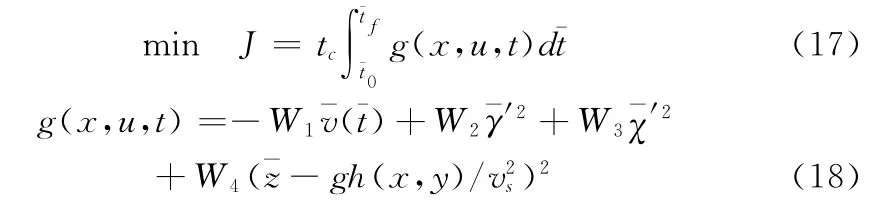
其中:x、u分别代表载机的状态量和控制量,通过上文分析易得, t0、tf分别表示规划起始与结束时的时刻;式(18)右边第一项表示决策时希望航程尽可能小,第二、三项表示使航迹尽量平滑,第四项是表示希望尽量降低飞行高度。W1、W2、W3、W4表示各项的权重。
2.2 对地攻击航迹控制决策最优控制模型
通过2.1小节建立的指标函数以及第1节得到的飞行状态模型与各类约束模型可得到对地攻击航迹控制决策最优控制模型如下:
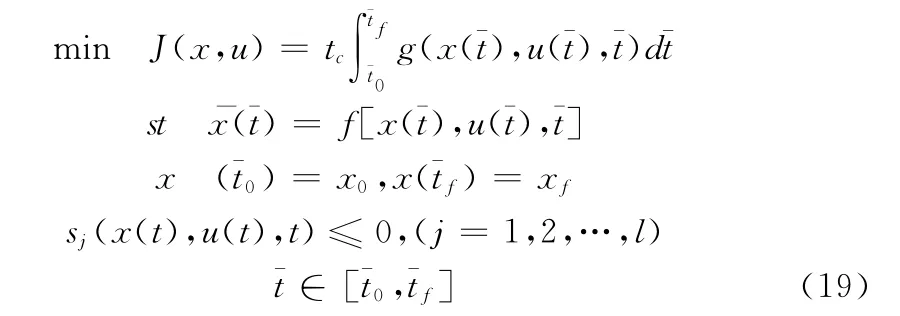
其中:目标函数对应式(17);状态方程对应式(7);边值条件和不等式对应约束条件,包括初始与终止点约束以及威胁约束。
3 基于滚动粒子群算法的战斗机对地攻击轨迹控制决策
粒子群算法[7]是一种思想直观、实现简单且执行效率很高的智能算法。目前,粒子群算法在航迹规划中的应用已经相当成熟。但粒子群算法在航迹规划中的应用主要集中于规划出一条较优的航迹,对于如何实现控制量的决策从而实现在线控制,粒子群算法则显得略为无力。因此,本文将结合滚动时域控制与粒子群算法实现在线决策,解决战斗机对地攻击轨迹控制决策问题。
3.1 算法描述
3.1.1 滚动时域控制
滚动时域控制(RHC)[8]的基本思想是:将规划时域[tk, tk+T]进行离散采样,取离散点,在每一个离散时刻,用系统当前的状态作为初始条件,求解出规划时域内的最优控制序列uk,在该离散时刻只取控制序列uk中的第一项作用于系统以获得系统新的状态,再将新状态作为初始时刻重复执行上述操作,直到达到末段约束条件。为直观理解其作用原理,绘制原理如图4所示。
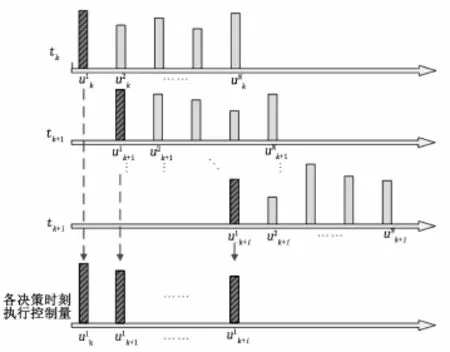
图4 滚动时域控制原理
3.1.2 粒子群算法描述
粒子群算法最早是在1995年由Eberhart和Kennedy[6]共同提出来的,其基本思想是受到他们早期对许多鸟类的群体行为进行建模与仿真研究结果的启发:在鸟群的迁徙过程中,每个个体能够通过一定的规则估计自身位置的适应值;每个个体能够记住自己到目前位置找到的最佳位置,称为“局部最优pbest”;此外还能记得群体中所有鸟中找到的最佳位置,称为“全局最优gbest”。这两个最优变量使得鸟儿在某种程度上朝这些方向靠近。综合这些内容,提出了我们所说的粒子群算法。
在粒子群算法中,每个个体被称为“粒子”,每个粒子都代表着一个潜在的解。在n维搜索空间中,每一个粒子都看做是空间中的一个点。设群体中有m个粒子,则m称为群体规模,过小的m会导致寻优结果不理想,过大的m值会影响算法的运算速度。假设在第t次迭代中,第i个粒子的位置为Xi=(xi1,xi2,…,xin),根据事先规定的适应度函数可以计算当前位置的优劣;为粒子i的飞行速度,即粒子移动的距离;为粒子到目前为止经过的最优的位置为整个粒子群迄今为止搜索到的最佳位置gbest。
在每次迭代中,粒子速度与位置的更新如下所示:

其中:ω为惯性权重;c1、c2为学习因子,也称加速因子,其使粒子具有自我总结和向群体中优秀个体学习的能力;r1、r2为[0,1]之间的随机数,这两个参数的作用是为了保持群体多样性。式(20)中的第二部分是“认知”部分,代表了粒子对自身的学习;而第三部分是“社会”部分,代表了粒子间的协作,正是基于以上两种学习思想,促使粒子向新的适应度更高的位置逼近。
3.2 滚动粒子群算法的实现
3.2.1 离散规划时域
首先将规划时域离散化,将每段规划时域[tk,tk+T]离散成N段,有:
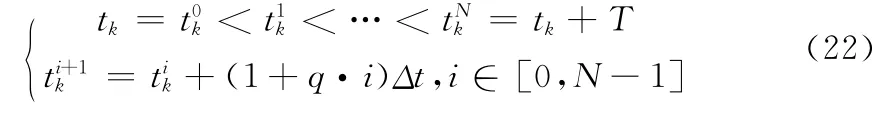
其中:q为时间步长增长率。通过如上的离散化之后,结合提出的最优控制模型,我们可以将一个规划时域内的最优控制模型离散化作如下表示:
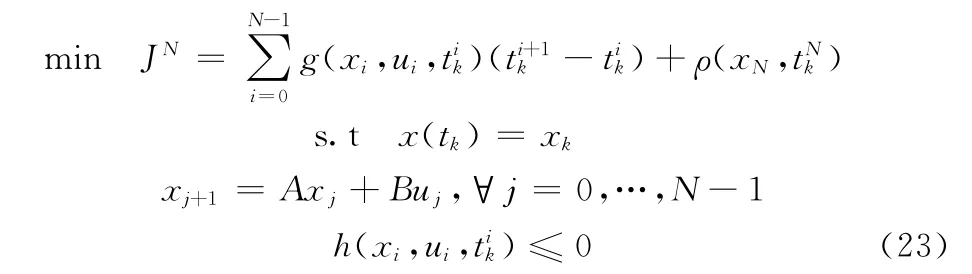
为简化计算,在本文的仿真计算中取N=2。结合滚动时域控制的思想,即在每个规划时域内求取两阶段的最优控制量,只取第一阶段所得作用于系统。
3.2.2 粒子群算法的编码方式与基本流程
采用粒子群算法求取每个规划时域内的最优控制量,本文采用十进制的编码方式,即每个粒子的信息由6个十进制的数字表示,前3个数字表示第一阶段的控制量,后3个数字表示第二阶段的控制量。对规划时域内两个阶段的控制量进行编码,编码方式如下[9]:
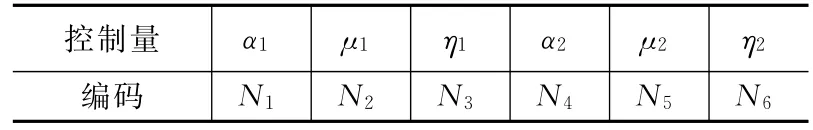
表1 控制量编码方式
通过一定的方法,将编码转化为控制量(解码),以控制量α为例,转化公式:

Δα表示攻角的变化率,当所求的攻角大于载机攻角的最大值时,攻角控制量取其最大值;小于最小值时,取最小值。其它控制量也依此方法进行解码。
粒子群算法的基本流程如下:
步骤1:设置最大迭代次数、群体规模、惯性权重、学习因子等算法参数;
步骤2:初始化各粒子的的位置Xi和速度Vi;
步骤3:计算每个粒子的适应度,确定pbest和gbest;
步骤4:将每个粒子的适应度值与pbest比较,并将其中较好的赋值给pbest;
步骤5:将每个粒子的适应度与当前的gbest比较,将较好的赋值给gbest;
步骤6:根据公式(20)(21)更新粒子的位置和速度;
步骤7:判断是否满足要求或者达到最大迭代次数,若满足,算法进行至下一步,不满足则跳转回第3步;
步骤8:取当前gbest为最优解。
3.2.3 滚动粒子群算法的实现流程
以上给出了对于规划时域的离散化方法以及粒子群算法的基本步骤,滚动粒子群算法的实现流程如图5所示。
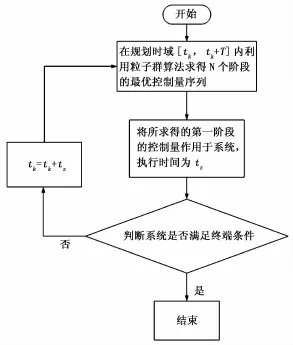
图5 滚动粒子群算法流程
如图5所示,在滚动时域控制的实现过程中,首先在规划时域[tk,tk+T]内应用粒子群算法,得到该时域内N个阶段的最优控制量,组成最优控制量序列,采用该序列中的第一项作用于系统,执行时间记为tz;执行结束后判断系统状态,若满足终端条件,则算法运行完毕,若不满足则以执行完上一控制量的时刻为新的规划时域起点,求解新的规划时域内的最优控制量序列并作用于系统。重复进行上述操作。
3.3 仿真分析
战场环境:假设战机从地理坐标系(130 km,38 km)海拔5 km处出发攻击位于(103.5 km,71.5 km)处的目标,选择合适的武器进行攻击,所选武器的发射区域为开口方向230°,展开角60°,半径5 km的扇形区域。作战区域内存在两处雷达探测威胁,两部雷达的坐标分别为(112.82 km,72.27 km),(108.16 km,44.47 km),雷达架高50米,发射功率100 kw,增益10 dB,波长0.1m,接收机灵敏度取10-13W。
战机性能:战机最小RCS为0.15 m2,最大RCS为1.25 m2;战机最小安全高度为200 m;战机质量m=2 000 kg,S =50 m2。受作战任务以及战机自身性能的约束,在执行任务的过程中对战机的各个控制量以及状态量作出如下要求:100 ≤v≤350;2°≤γ≤90°;-180°≤γ≤180°;-2°≤α≤15°;-60°≤μ≤60°;0≤η≤1。战机的初始状态如下:t0=0;v0=256;γ0=0°;α0=6°;μ0=0°;η0=0.2。终端约束:战机进入如上所述的发射区。
算法参数:W1、W2、W3、W4各项权重取(0.4,0.2,0.2,0.2);N=2;步长增长率q=1 s;规划时域长T=3 s;仿真步长0.1 s;决策执行时间tz=0.5 s;粒子数m=50,惯性权重ω=0.5,学习因子c1=c2=1.5,最大迭代次数50。经过仿真分析得图6。
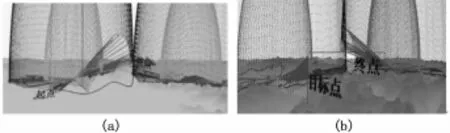
图6 对地攻击轨迹示意图

图7 控制量变化规律
在VC环境下进行仿真,图6中蓝色的包络表示当载机的RCS取最大值时,威胁区域的大小,红色包络表示当RCS取最小值时威胁区域的大小。可以看出,由于地形遮蔽的作用,在两处雷达探测威胁中间形成了一定的威胁盲区,载机利用该盲区以及自身RCS随飞行姿态的动态变化,保证战机始终处于探测威胁之外。图6(b)中的扇形表示武器的发射区,可见通过滚动粒子群算法,载机顺利地突进进入武器的可发射区以便实现对目标的攻击。图7显示了攻角、横滚角、推力系数这3个控制量随着决策次数的变化规律,据此可以给飞行员带来操纵参考,从而实现对飞行员的辅助。图8表示了航迹方位角、航迹倾斜角以及载机速度的变化规律,可以看出各个状态亮的变化都比较缓和,从而体现了所规划航迹的可操纵性。

图8 状态量变化
4 结论
针对空对地攻击的航迹控制问题,建立相关模型,选取控制量与状态量,根据作战任务要求确定航迹控制问题的指标函数,将各类威胁简化为约束条件从而将航迹控制问题转化为最优控制问题。将粒子群算法与滚动时域控制相结合,利用粒子群算法求解每个决策时域内的控制量最优值,再利用滚动时域控制在线滚动更新时域,实现在线实时控制。通过仿真验证该方法切实可行,能够规划出一条适当的战机航迹并且能提供各个控制量的变化规律,为飞行员操纵载机提供了辅助决策,提升作战效能。
[1]张 煜,张万鹏,等.基于Gauss伪谱法的UCAV对地攻击武器投放轨迹规划[J].航空学报,2011,32(7):1240-1251.
[2]陈中起.先进战斗机突击任务规划关键技术研究[D].西安:空军工程大学,2011.
[3]黄长强,黄汉桥,等.复杂不确定环境下UCAV自主攻击轨迹优化设计[J].西北工业大学学报,2013,31(3):331-338.
[4]张 赢,汪荣峰,廖学军.数字地图图幅接边的虚拼接算法[J].计算机工程与设计,2010,31(6):3640-3643.
[5]吴宗一.协同作战条件下空空导弹作战效能研究[D].西安:空军工程大学大学,2009.
[6]任 波,于 雷,周 焘.一种低空突防的雷达地形遮蔽盲区算法研究[J].电光与控制,2008,15(1):10-11.
[7]纪 震,廖惠连,吴青华.粒子群算法及应用[M].北京:科学出版社,2009.
[8]Zhan Z H,Zhang J,Li Y.An efficient ant colony system based on receding horizon control for the aircraft arrival sequencing and scheduling problem[J].IEEE Transactions on Intelligent Transportation Systems,2010,11(2):399-412.
[9]张 涛,于 雷,周中良,等.基于混合算法的空战机动决策[J].系统工程与电子技术,2013,35(7):1445-1450.
Air-to-Ground Attack Decision-Making of Controlling Trajectory Based on RHC-PSO
Lei Pengfei1,Wei Xianzhi1,Gao Xiaomei2,Wang Zhihong1
(1.School of Aeronautics and Astronautics,Air-force Engineering University,Xi′an 710038,China;2.Equipment Department of China PLA Nanjing Military Region Air Force,Nanjing 210000,China)
Aiming at the controlling of trajectory during the air-to-ground attack,firstly,the 6 DOF model of combat aircraft,allround RCS model and the model of the threats are established.Choosing the thrust coefficient、angle of attack、roll angle as the controlled quantity.Then established the indicator function and the optimum control modeling of the air-to-ground trajectory decision-making.A-dopt the RHC-PSO algorithm,getting the controlled quantity’s optimum value in every decision-making time domain,combining the RHC to realize online controlling of the trajectory.Simulation shows that the algorithm can control the aircraft to perform the operational mission and show the change law of the controlled quantity,giving the information of aid decision making to pilot.
air-to-ground attack,control of trajectory;RHC-PSO;aid decision making
1671-4598(2016)08-0145-05
10.16526/j.cnki.11-4762/tp.2016.08.039
:E844
:A
2016-04-23;
:2016-05-19。
雷鹏飞(1992-),男,西安人,主要从事武器系统总体技术与作战运用方面的研究。
