小波包变换中地震信号的结点序号到频带序号的转换算法

白 泉, 韩晶晶, 康玉梅, 边晶梅

(1.沈阳工业大学建筑与土木工程学院,辽宁 沈阳 110870; 2.贺州学院建筑工程学院,广西 贺州 542899;3.东北大学资源与土木工程学院,辽宁 沈阳 10004; 4.沈阳化工大学经济与管理学院,辽宁 沈阳 110142)

技术交流

小波包变换中地震信号的结点序号到频带序号的转换算法

白 泉1, 韩晶晶2, 康玉梅3, 边晶梅4

(1.沈阳工业大学建筑与土木工程学院,辽宁 沈阳 110870; 2.贺州学院建筑工程学院,广西 贺州 542899;3.东北大学资源与土木工程学院,辽宁 沈阳 10004; 4.沈阳化工大学经济与管理学院,辽宁 沈阳 110142)

利用小波包变换对地震非平稳信号进行处理时,结点与频带之间存在“跳频”现象,基于小波包变换算法以及异或运算,对小波包树频带序号和结点序号的关系进行研究,明确信号子空间频带与小波包树结点的排列规律,同时提出一种从结点序号到频带序号的转换算法。基于MATLAB平台,以唐山(南北向)波为例,验证该算法的正确性。

小波包; 树结点; 频带排列; 异或运算

0 引言

地震动分析是研究地震危害控制的基础,也是控制地震危害的前提。小波包变换可将地震信号均匀分解到不同的频带上,从而能够准确分析各个频带上地震信号的详细特征。但在MATLAB平台中,由于算法的限制,小波包变换后得到的频带顺序与小波包树结点顺序并不一致,反而会出现“跳频”现象[1-4]。若忽视这一问题,就不能准确定位频带,

进而影响后续时频分析的正确性[5],因此明确频带与小波包树结点的对应关系对时频分析意义重大。

本文基于MATLAB平台,借助小波包算法和异或运算定义,主要对小波包变换后的频带序号和树结点序号的关系进行研究,指出信号子空间频带与小波包分解树结点的排列规律,提出一种从结点序号到频带序号的转换算法,并举例验证该转换算法的正确性,这对提取地震信号局部特征、有层次地展现地震信号等具有重要意义。

1 小波包理论

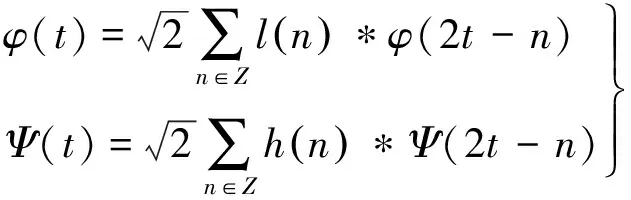
(1)

利用滤波器组实现小波包变换的关键是隔点下采样,采样后分信号与原信号的关系为[2]:

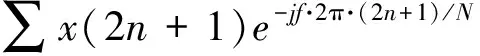
(2)

X(N/2+f)=∑x(2n)e-j(N/2+f)·2π·2n/N+ ∑x(2n+1)e-j(N/2+f)·2π·(2n+1)/N

(3)

式中:X(f)表示x(n)的离散傅里叶变换;N为采样点数。由式(2)和(3)可得:

X′(f)=0.5[X(f)+X(N/2+f)]

(4)

式中:X′(f)为下采样后得到的序列的傅里叶变换。由离散傅里叶变换的对称性可知:

X(N/2+f)=X(N/2-f)

(5)

将式(5)代入式(4)中可得:

X′(f)=0.5[X(f)+X(N/2-f)]

(6)

根据采样定理,当X(f)的采样频率为f0时,其有效频段为(0,f0/2),故X′(f)的采样频率为f0/2,有效频段为(0,f0/4),且有:

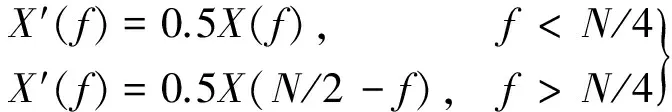
(7)

由此可以清楚地分析小波包分解信号的过程:当信号采样频率为2f时,其有效频段为(0,f),在小波包变换中,经过低通和高通滤波器进行第一层分解后,整个频带被划分为低频频带L(0,f/2)和高频频带H(f/2,f);对这两个频带的信号进行下采样后再分别进行第二次分解,每个频带又被划分为两个频带,其中低频频带划分得到(0,f/4)和(f/4,f/2)频带,高频频带划分得到(f/2,3f/4)和(3f/4,f)频带;如此不断重复低频频带和高频频带的二进划分,就可以分离出不同频带,从而实现了对频带的均匀细分[1,3,7]。

小波包分解过程可以用分解树来描述,如图1所示。图中Uj,n表示小波包分解的子空间编号,亦可称作结点编号;j表示分解层数,其对应的分解尺度为2j,第j层一共有2j个正交基;n表示第j分解层的子空间编号,第j层的第n个子空间由集合{uj,n(t-k)}构成。

由小波包变换理论知识可知,同一层的各个子空间之间相互正交且每一层上所有子空间的直和构成这个信号空间。

2 地震信号频带划分参数

对地震动非平稳信号进行小波包变换时,主要参数有分解层数和分解路径。

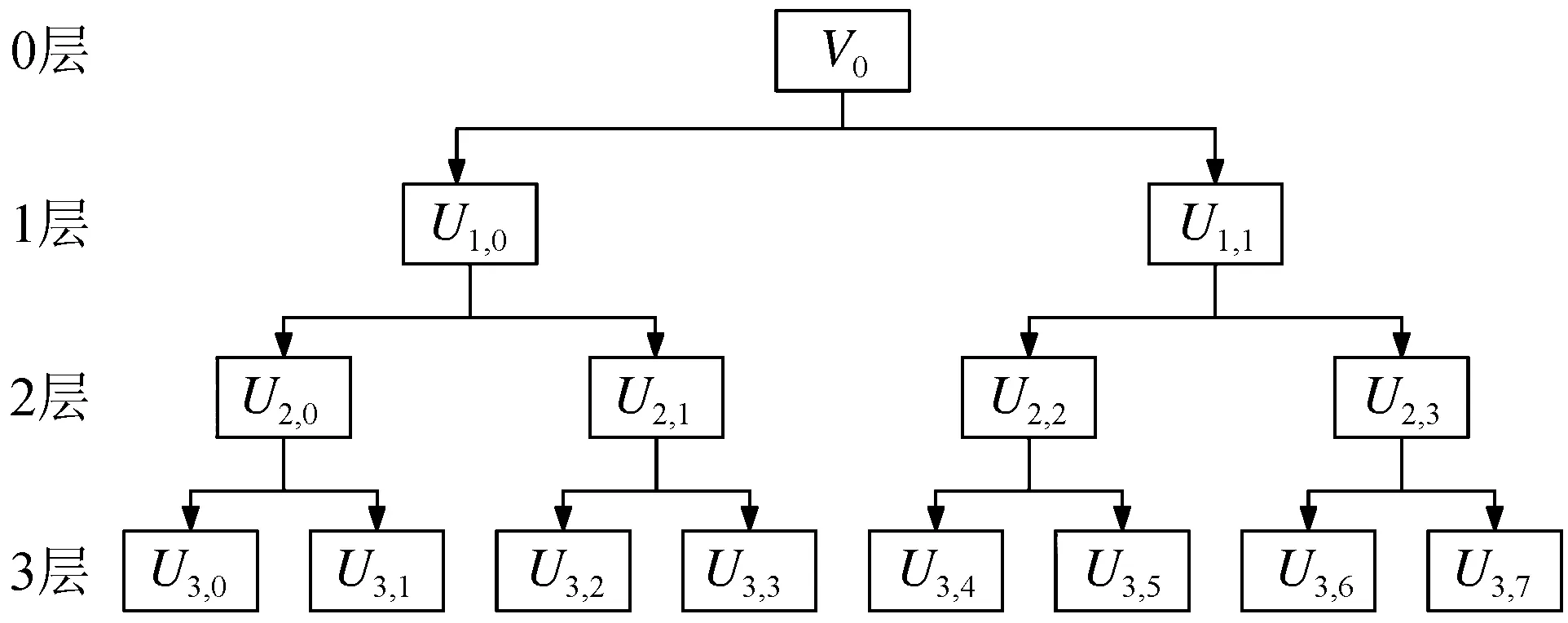
图1 小波包分解Fig.1 Wavelet packet decomposition

2.1 分解层数

在进行小波包分解时,除了确定小波基函数,还需要确定分解层数。这里选用字母j表示小波包分解层数,通常分解层数按下式选取[2,7]:

(8)

式中:Ls为输入信号的长度。对于地震非平稳信号,采样时间间隔一般为0.01 s或0.02 s,即采样频率为100 Hz或50 Hz。地震动信号一般持续时间为10～20 s,若采样频率为50 Hz,则信号长度约为29～210。综合考虑频带宽度及分辨率,本文认为分解层数取7一般能满足地震信号的分析要求。

2.2 分解路径

如上所述的小波包分解树中,树结点从左至右依次编号为0,1,2,…2j-1,称作结点序号。地震信号的小波包分解实际上是把信号通过一组滤波器组合(低通或高通)后,到达底端的树结点。设定0表示低通滤波,1表示高通滤波,则各滤波器组合可由一个二进制数表示[8],称该二进制数为实际路径。例如,实际路径101表示信号经过一次高通滤波器,一次低通滤波器,最后又经过一次高通滤波器,如图2中虚线所示。该二进制数对应的十进制数就是分解终端树结点的频带序号,因此实际路径又称频带路径。与频带路径相对应,把结点序号的二进制数称作结点路径或理想路径。

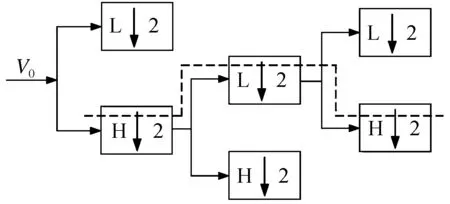
图2 101分解路径Fig.2 Decomposition path 101

除了频带路径和结点路径,每个结点还对应一个通频带。通频带是指通过该结点的频带范围,与频带序号有关。若信号的有效频带为f,分解层数为j,则频带序号m对应的通频带为m*(f/2j)-(m+1)*(f/2j),其中m=0,1,2,…,2j-1。

需要说明的是,分解层数和分解路径之间存在的关系:分解路径的每个二进制数的位数即为获得该频带所需要的分解层数,这样可以准确获取各个频带分解路径,尤其是以0开头的分解路径,同时为后续准确得到频带序号及对应的通频带做铺垫。

3 频带序号与结点序号的变换

3.1 小波包分解的频带排列规律

地震信号经过小波包分解后,可看作由每层所有子空间组合构成。小波包分解采用隔点采样算法,得到的频带信号分解分量按照自然序号排列,而不是频率由小到大排列,因此各个频带信号之间存在排序紊乱现象。若想对各频带分信号进行准确分析,就需要找到其实际的频带序号排列规则。

通过对多个信号进行不同层次的小波包分解总结,得到的规律如下:由高通滤波器得到的频段,进行下一阶段滤波时高低频段要发生位置互换。这有助于准确定位所需频段对应的小波包树结点,将其用小波包树的形式表示出来,如图3所示。

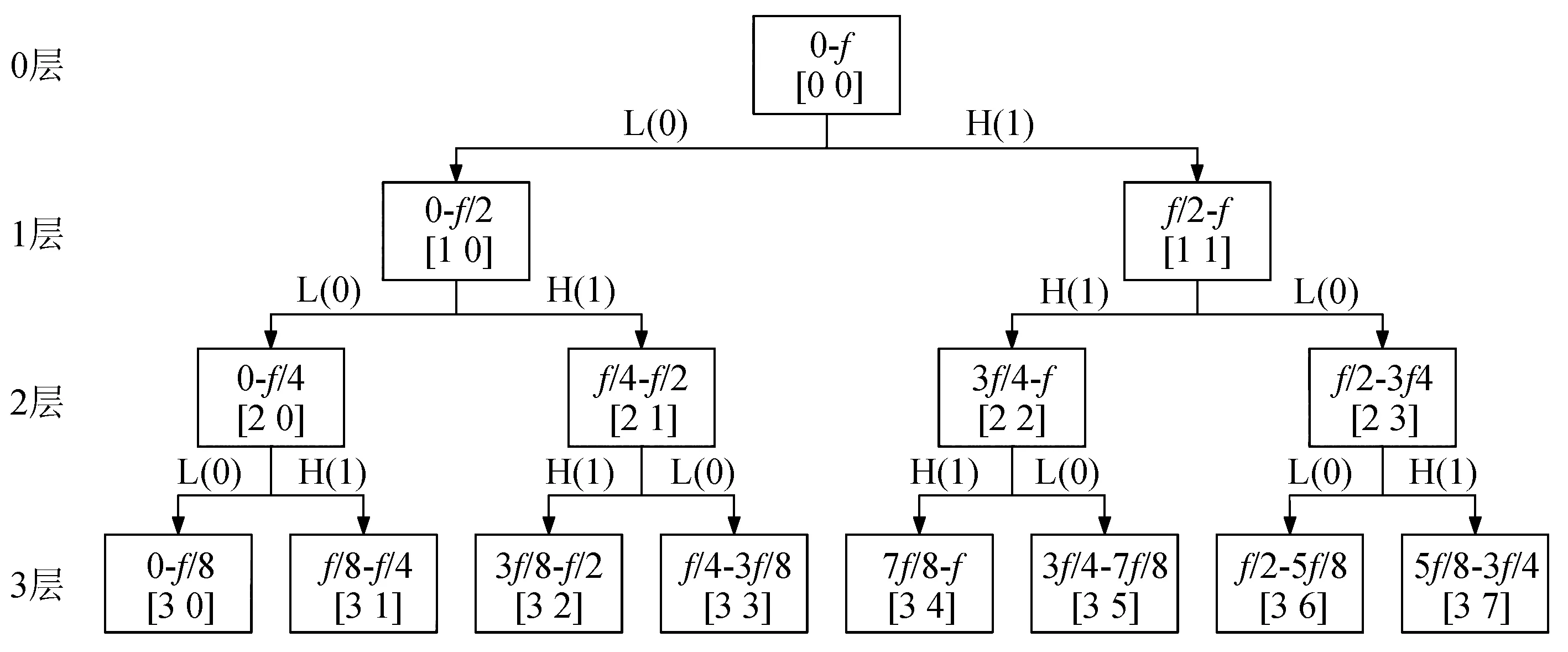
图3 对应频带的小波包分解树Fig.3 Wavelet packet decomposition tree of corresponding frequency band

由图3可知,小波包空间分解的子频带按照结点序号顺序排列时,并不是完全按照频率递增顺序排列的。比如,对于分解的第三层,结点序号依次为0,1,2,3,4,5,6,7,是自然顺序,而频带序号依次为0,1,3,2,7,6,4,5。这种排列顺序验证了上述规律的正确性,即由高通滤波器得到的频段进行下一阶段滤波时,高低频段要发生位置互换。

3.2 结点序号到频带序号的转换关系

当分解层数较少时,可以根据上述规律手动依次得到每个结点的频带路径和通频带,进而得到完整的小波包树。但是当分解层数较多时,手动获取比较困难,因此需要找到结点序号到频带序号之间的换算关系。

按照图3的3层小波包分解树可以得到每个结点的结点分解路径和频带分解路径。比如,第3层小波包分解结点序号为7的结点,其结点路径为111,对应的频带滤波路径为HLH,可得到频带路径为101,对应的频带序号为5,通频带为(5*f/23,6*f/23)。通过多个结点的分析,得到结点序号到频带序号的转换过程:

对结点序号进行二进制转换得到结点分解路径(一个二进制数),从左至右对该路径的每位二进制数与其左侧所有位数进行异或运算,得到频带分解路径(一个新的二进制数),对新的二进制数进行十进制转换,即可得到频带序号。比如,经过3层小波包分解得到的小波包树,结点序号为a,a的结点分解路径的二进制数为ABC,异或运算后的频带分解路径二进制数为XYZ,则X=A、Y=A⨁B、Z=A⨁B⨁C,对二进制数XYZ转化为十进制数b,则b即为结点a对应的频带序号。

上述的“异或”是一种数学逻辑运算符,数学符号为“⨁”,计算机符号为“XOR”,其运算法则为:

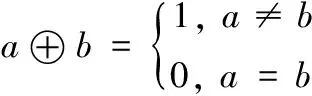
(9)

根据上述换算过程和运算法则,在MATLAB平台上编制程序,可以实现小波包分解到任意分解层数时,地震信号的结点序号与频带序号的转换。表1为7层小波包变换下的结点序号与经过上述转换得到的频带序号。

4 实例验证

选取唐山波南北向(北京观测)的强震记录进行实例分析,验证本文所述地震信号频带特性分析中频带序号与结点序号之间转换算法的正确性。地震信号采样点数为2 000,采样的时间间隔为0.01 s,采用sym5小波函数,在MATLAB平台上编制程序对唐山波进行7层小波包变换,得到各树结点的频谱图。本例中,采样频率为100 Hz,根据采样定理,有效频率为0～50 Hz,进行7层分解后每个频带宽度为f/27,即50/27Hz。限于篇幅,给出结点序号分别为11、12、34、36、53、55的频谱图,如图4所示。

表1 结点序号与频带序号

续表1

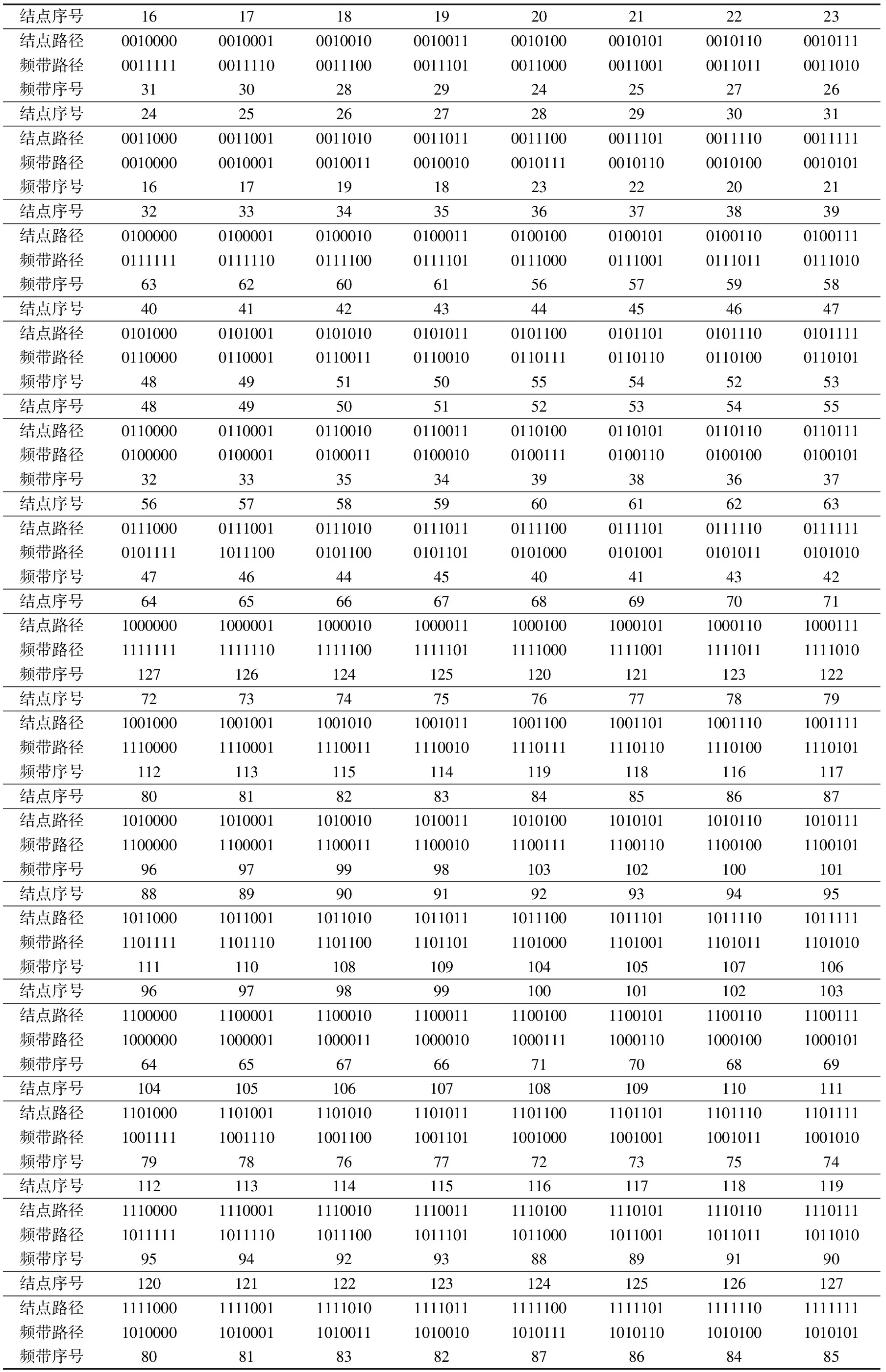
结点序号1617181920212223结点路径00100000010001001001000100110010100001010100101100010111频带路径00111110011110001110000111010011000001100100110110011010频带序号3130282924252726结点序号2425262728293031结点路径00110000011001001101000110110011100001110100111100011111频带路径00100000010001001001100100100010111001011000101000010101频带序号1617191823222021结点序号3233343536373839结点路径01000000100001010001001000110100100010010101001100100111频带路径01111110111110011110001111010111000011100101110110111010频带序号6362606156575958结点序号4041424344454647结点路径01010000101001010101001010110101100010110101011100101111频带路径01100000110001011001101100100110111011011001101000110101频带序号4849515055545253结点序号4849505152535455结点路径01100000110001011001001100110110100011010101101100110111频带路径01000000100001010001101000100100111010011001001000100101频带序号3233353439383637结点序号5657585960616263结点路径01110000111001011101001110110111100011110101111100111111频带路径01011111011100010110001011010101000010100101010110101010频带序号4746444540414342结点序号6465666768697071结点路径10000001000001100001010000111000100100010110001101000111频带路径11111111111110111110011111011111000111100111110111111010频带序号127126124125120121123122结点序号7273747576777879结点路径10010001001001100101010010111001100100110110011101001111频带路径11100001110001111001111100101110111111011011101001110101频带序号112113115114119118116117结点序号8081828384858687结点路径10100001010001101001010100111010100101010110101101010111频带路径11000001100001110001111000101100111110011011001001100101频带序号96979998103102100101结点序号8889909192939495结点路径10110001011001101101010110111011100101110110111101011111频带路径11011111101110110110011011011101000110100111010111101010频带序号111110108109104105107106结点序号96979899100101102103结点路径11000001100001110001011000111100100110010111001101100111频带路径10000001000001100001110000101000111100011010001001000101频带序号6465676671706869结点序号104105106107108109110111结点路径11010001101001110101011010111101100110110111011101101111频带路径10011111001110100110010011011001000100100110010111001010频带序号7978767772737574结点序号112113114115116117118119结点路径11100001110001111001011100111110100111010111101101110111频带路径10111111011110101110010111011011000101100110110111011010频带序号9594929388899190结点序号120121122123124125126127结点路径11110001111001111101011110111111100111110111111101111111频带路径10100001010001101001110100101010111101011010101001010101频带序号8081838287868485

按照本文给出的变换算法,参照表1的频带序号与结点序号的对应关系,取图4中的各点如表2所列。

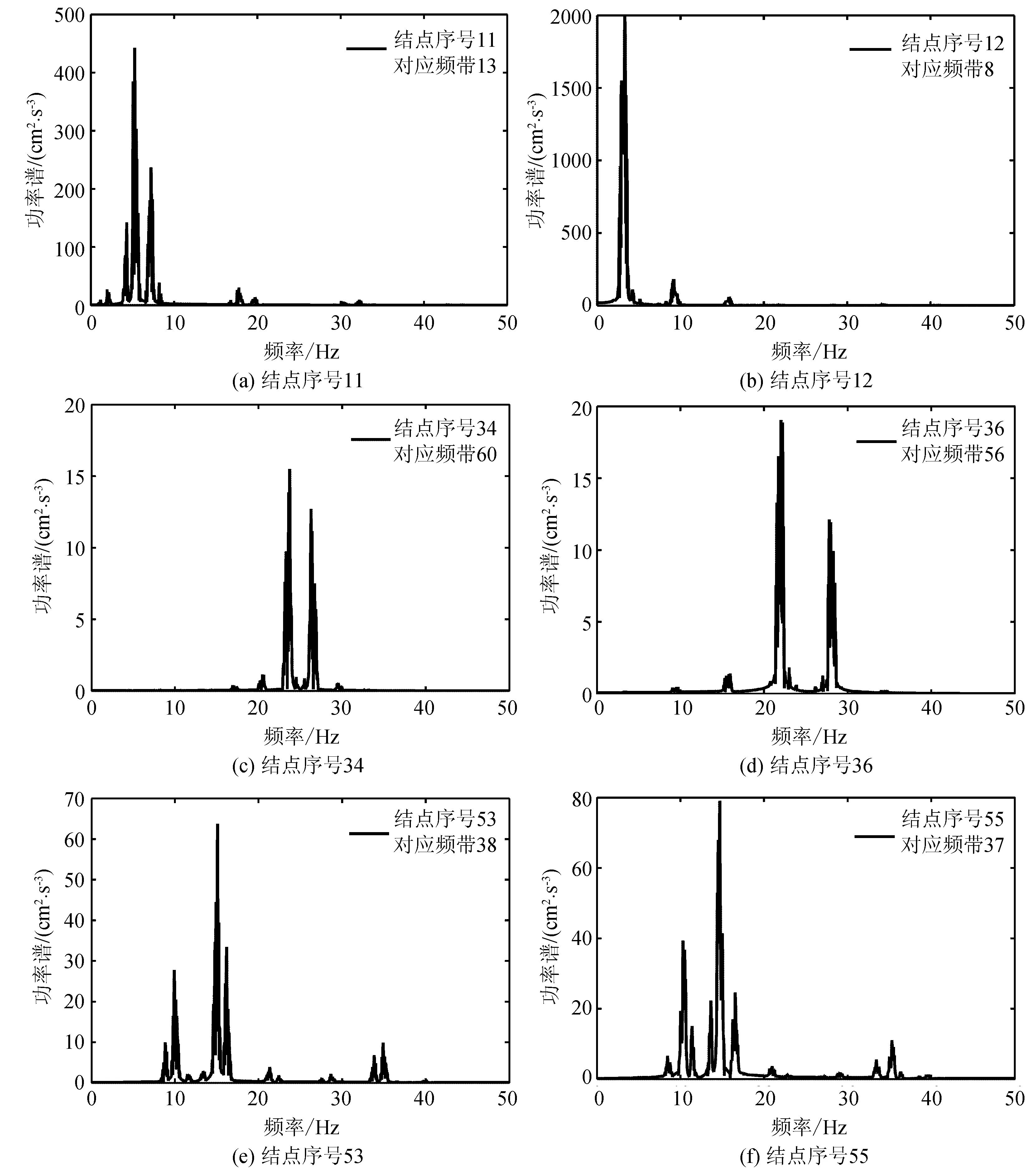
图4 树结点频谱Fig.4 Spectra of tree nodes

结点序号频带序号通频带结点序号频带序号通频带11135．078～5．468365621．875～22．2661283．125～3．516533814．844～15．234346023．437～23．828553714．453-14．844注：频带序号m对应的通频带为m∗(f/2j)-(m+1)∗(f/2j)，单位为Hz。

5 结论

小波包变换可将地震信号均匀分解到不同的频带上,但由于算法限制,变换后得到的树结点顺序与频带顺序并不一致,即“跳频”。本文针对这一问题,基于MATLAB平台对小波包变换中小波包分解树结点序号与频带序号所存在的错乱现象进行了简单介绍,并从小波包算法和异或运算的角度,通过滤波器组的基本原理来实现小波包变换的算法,明确并分析了频带均匀划分理论。借助分解路径,总结了小波包变换的频带顺序排列规律,并由此得到了小波包分解树的结点序号转换到频带序号的算法,为确定频带和小波包分解树各结点的对应关系提供了一种有效的方法。若不考虑能量泄漏,图中给出的各结点通频带范围与本文所提供的转换算法结果基本一致,由此验证了本文所述地震信号从结点序号转换到频带序号的算法的正确性,对有层次地展现地震信号等工程应用具有重要意义。

References)

[1] 曾宇清,王卫东,贺启庸.按频带顺序排列的小波包新算法及应用[J].力学学报,1998,30(2):186-192. ZENG Yu-qing,WANG Wei-dong,HE Qi-yong.Theory and Application of New Wavelet Packets Algorithm with Results in Order of Frequency-bands[J].Acta Mechanica Sinica,1998,30(2):58-64.(in Chinese)

[2] 薛蕙,杨仁刚,郭永芳.小波包变换(WPT)频带划分特性的分析[J].电力系统及其自动化学报,2003,15(2):5-8. XUE Hui,YANG Ren-gang,GUO Yong-fang.Frequency Division Character of Wavelet Packet Transform[J].Proceedings of the EPSA,2003,15(2):5-8.(in Chinese)

[3] 曾宪伟,赵卫明,盛菊琴.小波包分解树结点与信号子空间频带的对应关系及其应用[J].地震学报,2008,30(1):90-96. ZENG Xian-wei,ZHAO Wei-ming,SHENG Ju-qin.Corresponding Relationships between Nodes of Decomposition Tree of Wavelet Packet and Frequency Bands of Signal Subspace[J].Acta Seismologica Sinica,2008,30(1):90-96.(in Chinese)

[4] V L Pham,K P Wong.Antidistortion Method for Wavelet Transform Filter Banks and Nonstationary Power System Waveform Harmonic Analysis[J].IET Proceedings-Generation,Transmission and Distribution,2001,148(2):117-122.

[5] 许康生,李英,李秋红.近地震波的小波相对能量分布特征分析[J].地震工程学报,2013,35(1):166-170. XU Kang-sheng,LI Ying,LI Qiu-hong.Distribution Characteristics of Wavelet Relative Energy on Near-earthquake Wave[J].China Earthquake Engineering Journal,2013,35(1):166-170.(in Chinese)

[6] 彭玉华.小波变换与工程应用[M].北京:科学出版社,1999:21-69. PENG Yu-hua.Wavelet Transform and Engineering Application[M].Beijing:Science Press,1999:21-69.(in Chinese)

[7] 杨世锡,项文娟,叶红仙.基于Lab-VIEW的机械故障信号小波包分解和重构[J].机电工程,2007,24(7):14-16. YANG Shi-xi,XIANG Wen-juan,YE Hong-xian.Decomposition and Reconstruction with Wavelet Packet of Mechanical Fault Signals Based on Lab-VIEW.[J].Mechanical & Electrical Engnering Magazine,2007,24(7):14-16.(in Chinese)

[8] 吝伶艳,宋建成,谢特列.小波包频带检索改进算法及其在电机故障诊断中的应用[J].太原理工大学学报,2012,43(3):391-395. LIN Ling-yan,SONG Jian-cheng,XIE Te-lie.The Improved Algorithm of Wavelet Packet Frequency Band Retrieval and Its Application in Motor Fault Diagnosis[J].Journal of Taiyuan University of Technology,2012,43(3):391-395.(in Chinese)

Conversion Algorithm from Order Number of Nodes to that of Frequency Bands for Seismic Signals Using Wavelet Packet Transform

BAI Quan1, HAN Jing-jing2, KANG Yu-mei3, BIAN Jing-mei4

(1.SchoolofArchitectureandCivilEngineering,ShenyangUniversityofTechnology,Shenyang110870,Liaoning,China; 2.SchoolofArchitecturalEngineering,HezhouUniversity,Hezhou542899,Guangxi,China; 3.CollegeofResourcesandCivilEngineering,NortheasternUniversity,Shenyang110004,Liaoning,China; 4.SchoolofEconomicsandManagement,ShenyangUniversityofChemicalTechnology,Shenyang110142,Liaoning,China)

The "frequency hopping" phenomenon often occurs when using the wavelet packet transform to process non-stationary seismic signals. To solve this problem, we examine the relationship between the order number of the wavelet packet tree bands and the order number of the nodes, based on the wavelet packet transform and exclusive or (XOR) operation algorithm. We clarify the arrangement rule between the frequency bands of the signal subspace and the tree nodes of the wavelet packet. Moreover, we propose a conversion algorithm for seismic signals from the order number of the nodes to that of the frequency bands. Based on the MATLAB platform, we use the Tangshan wave (NS direction) as an example and verify the correctness of the algorithm.

wavelet packet; tree node; frequency bands arrangement; XOR algorithm

2015-12-25 基金项目:国家自然科学基金(51204029,51308348);辽宁省教育厅基金项目(L2013050);贺州学院自然科学基金资助项目(2016ZZZK06)

白 泉,男,副教授,主要从事随机荷载模拟及结构动力反应分析等方面的研究。E-mail:baiquan@163.com。

韩晶晶，女，助教，主要从事地震动特性分析及地震荷载模拟等方面的研究。E-mail:hanjingjing_stu@163.com。

P315.3+1

A

1000-0844(2016)06-0991-06

10.3969/j.issn.1000-0844.2016.06.0991