径向基函数插值中的一种新的重启动策略

齐 静

(重庆师范大学涉外商贸学院 数学与计算机学院,重庆 合川 401520)



径向基函数插值中的一种新的重启动策略

齐 静

(重庆师范大学涉外商贸学院 数学与计算机学院,重庆 合川 401520)

针对径向基函数插值方法,提出了一种新的重启动策略来改进径向基的优化效果.在采用SLHD(symmetryLatinHypercubedesign,对称拉丁超立方设计)方法换新的初始点对优化效果没有太大改进的时候,提出了一种更换径向基函数的重启动策略,可以取得更好的优化效果.通过数值算例说明了采用这种新的重启动策略在迭代次数上的优越性.

径向基函数;全局最优化;响应面模型;重启动策略;对称拉丁超立方设计

1 前言及预备知识

其中：f是一个确定性的连续函数,x∈Rd,‖x-xi‖表示x与中心点xi之间的欧氏距离,λi∈R,i=1,2,…,n.b∈Rd,a∈R.φ就是径向基函数，选定一个径向基函数φ之后,定义一个n×n的矩阵Φij:=φ(‖xi-xj‖)，i,j=1,2,…,n.

λi,b,a可以从下面的线性方程组中获得：

其中：

常见的径向基函数φ[2]取自于下面的5种：

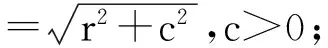
2 SLHD方法选取初始点

根据文献[3]中所介绍的拉丁超立方设计的矩阵(symmetry Latin Hypercube matrix),矩阵的每一列都是由{1,2,…,n}随机生成的.对称的拉丁超立方具有下列性质:在一个n×d的对称拉丁超立方矩阵中,若(a1,a2,…,ad)是矩阵的某一行, 必有n+1-a1,n+1-a2,…，n+1-ad)是这个矩阵的另外一行.

3 径向基函数插值的算法步骤

本文采用文献[4]中的径向基插值算法的一般步骤.

Step 0：根据SLHD方法生成n个初始点.

Step 1：计算f(x1),f(x2),…,f(xn).

Step 2：计算minf(xi),medf(xi),maxf(xi).i=1,2,…,n.

令Rl=medf(xi)-minf(xi),Ru=maxf(xi)-medf(xi).若max(Rl,Ru)≥4min(Rl,Ru),则用φ(f(x))来替换f(x)，其中φ(x)[5]如下：

Step 3：构建响应面模型.根据给定的初始点x1,x2…,xn,以及它们的函数值f(x1)，f(x2)，…,f(xn),取定径向基函数φ,构建径向基函数模型sn(x).

φ(‖x-xi‖)+bTx+a.

其中：n0表示初始点的个数，N表示循环长度(通常令N=5).

Step 6:下一个迭代点xn+1取自于gn(y)的极小点[7].

其中：ln(y,xi)=0,i=1,2,…,n,ln(y,y)=1.

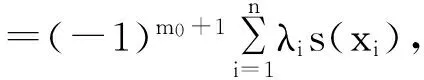
4 重启动策略

使用径向基插值算法在进行全局搜索时,算法可能会在某个局部极小点处进行较长时间的局部搜索,连续多次迭代都没有取得明显的实质性的进展,从而导致算法不能准确定位全局最优点.为了解决这个问题,文献[9]中提出一种使用新的SLHD的重启动策略.那么受文献[9]的启发,本文提出一种使用新的径向基函数的重启动策略.数值算例1说明了当采用文献[9]的使用新的SLHD策略对算法没有太大改进的时候,使用本文的换用新的径向基函数的策略可使算法减少迭代次数,从而快速收敛到全局最优点.

5 数值试验

例1考虑下面的问题:f(x)=-0.015 8x5+0.391 1x4-3.361 1x3+11.826 9x2-14.199 0x-1,x∈[0.2,1.2].(在此区间上的最优值为(0.898 8,-6.402 3)).

算法在局部极小点0.0000附近进行搜索,连续多次迭代都没有取得一些明显的进展,所得数据如表1所示.

表1 算法在局部极小点0.070 3附近进行较长时间的局部搜索
Tab.1 The algorithm near a local minimum point 0.070 3 for a long time local search

n值sn(x)的极小点sn(x)的极小值下一个点x(n+1)x(n+1)的函数值n值sn(x)的极小点sn(x)的极小值下一个点x(n+1)x(n+1)的函数值61.0000-6.20310.0571-1.7732191.0000-1.69550.0668-1.002571.0000-6.20360.0106-1.1495201.0000-1.69570.0667-1.000081.0000-6.21230.2296-1.0001211.0000-1.69580.0000-1.000291.0000-6.21940.9485-1.0005221.0000-1.69590.0000-1.0001101.0000-1.69120.2298-1.0000231.0000-1.69610.0000-1.0001111.0000-1.69230.2322-1.0000241.0000-1.69620.0001-1.0000121.0000-1.69300.9331-1.0000251.0000-1.69630.0000-1.0015131.0000-1.69360.0001-1.0000261.0000-1.69630.0000-1.0000141.0000-1.69410.0635-1.0001271.0000-1.69640.0000-1.0000151.0000-1.69450.9761-1.0000281.0000-1.69650.0000-1.0010161.0000-1.69480.0659-1.0015291.0000-1.69660.0000-1.0001171.0000-1.69510.0672-1.0000301.0000-1.69660.0000-1.0000181.0000-1.69530.0659-1.0000︙︙︙︙︙

分析表1的数据可知,算法在局部极小点x=0.000 0附近进行搜索,连续30-6=24(次)迭代都没有取得明显的进展,当没有改进的函数值的数量超过一个临界值(通常将这个临界值取为30)之后,采用文献[9]中的更换新的SLHD初始点的重启动策略.

采用文献[9]的更换新的SLHD的方法,算法仍然连续多次迭代都没有取得明显的进展,所得数据如表2所示.

分析表2的数据可知,使用文献[9]的换用新的SLHD的重启动策略,对算法的迭代情况并没有太大的改进.此时可以使用本文的更换径向基函数的重启动策略.

下面使用本文的更换径向基函数的重启动策略,径向基函数更换为:Φ(r)=r2log(r).

初始点：(0.235 3,-3.728 9),(1.143 9,-6.166 3),(0.139 4,-2.758 5),(1.027 3,-6.401 6),(0.022 8,-1.317 6),(0.931 4,-6.401 6).

使用本文的更换径向基函数的重启动策略,达到最优值所需迭代的次数为:11-6=5(次),所得数据如表3所示.

分析表3的数据可知,使用本文的更换径向基函数的重启动策略,可使算法及时跳出局部极小点,达到最优值所需迭代的次数为:11-6=5(次).

当算法连续多次迭代都没有取得明显进展的时候,可以使用本文的换用径向基函数的重启动策略,可使算法达到最优值的迭代次数减少.

表2 文献[9]的更换新的SLHD初始点的迭代情况Tab.2 Replace the new SLHD iterative initial point in literature[9]

表3 更换径向基函数,快速达到最优点Tab.3 Change the radial basis function,reach the most advantages quickly

6 小结

径向基函数具有计算格式简单、计算工作量小[10]等特点，在全局优化问题方面有着广泛的应用.利用径向基函数插值解决优化问题时,当使用文献[9]的换用新的SLHD的重启动策略对算法的优化效果并没有太大改进的时候,可以使用本文的换用新的径向基函数的重启动策略,可使算法及时跳出局部极小点,减少迭代的次数,加快收敛到最优点.

[1] HOLMSTRÖM K.An adaptive radial basis algorithm (ARBF) for expensive black-box global optimization[J].Journal of Global Optimization,2008,41:447-464.

[2] REGIS R G,SHOEMAKER C A.A quasi-multistart framework for global optimization of expensive function using response surface models[J].Journal of Global Optimization,2013,56:1719-1753.

[3] YE K Q,LI W,SUDJIANTO A.Algorithmic construction of optimal symmetric latin hypercube designs[J].Joumal of Statistial Planning and Inference,2000,90(1):145-159.

[4] 刘雨,刘广磊,姜自武,等.径向基函数插值配置点的自适应选取算法[J].应用数学进展,2016,5(1):8-14.

[5] 齐静.黑箱函数优化问题中的响应面优化方法[J].重庆工商大学学报(自然科学版)，2015,32(12):27-30.

[6] REGIS R G,SHOEMAKER C A.Constrained Global Optimization of Expensive Black Box Function Using Radial Basis Function[J].Journal of Global Optimization,2005,31:153-171.

[7] 吴宗敏.函数的径向基表示[J].数学进展,1998,27(3):202-208.

[8] BJÖRKMAN M,HOLMSTRÖM K.Global optimization of costly nonconvex functions using radial basis functions [J].Optimization and Engineering， 2000,4(1):373-397.

[9] REGIS R G,SHOEMAKER C A.Improved strategies for radial basis function methods for global optimization[J].Journal of Global Optimization,2007,37:113-135.

[10] 吴宗敏.散乱数据拟合的模型、方法和理论[M].北京：科学出版社,2007:82-83.

责任编辑：时 凌

A New Type of Restarting Strategy for Radial
Basis Function Interpolation

QI Jing

(School of Mathematics and Computer Science,Chongqing Normal University Foreign Trade and Business College,Hechuan 401520,China)

We propose a new restarting strategy to improve the optimization effect of the radial basis function interpolation method.When there is little improvement by using new initial points in the SLHD (symmetry Latin Hypercube design) method,we propose a restarting strategy of replacing the radial basis function which yields better numerical optimization performance. Then we illustrate the advantages of restarting strategy by some numerical examples.

radial basis function; global optimization; response surface model; restarting strategy;symmetry Latin Hypercube design

2016-07-16.

齐静(1990- )，女，硕士，主要从事全局最优化方法的研究.

1008-8423(2016)04-0398-04

10.13501/j.cnki.42-1569/n.2016.12.009

O241.6

A