基于水资源竞争的毒杂草入侵扩散模型稳定性分析

石 磊，刘 华*，蒋 芮，魏玉梅

(1.西北民族大学 数学与计算机科学学院，甘肃 兰州 730030；2.西北民族大学 实验中心，甘肃 兰州 730030)



基于水资源竞争的毒杂草入侵扩散模型稳定性分析

石 磊1，刘 华1*，蒋 芮1，魏玉梅2

(1.西北民族大学 数学与计算机科学学院，甘肃 兰州 730030；2.西北民族大学 实验中心，甘肃 兰州 730030)

以干旱地区植物对水资源的竞争环境为背景，考虑根系的分布范围，建立水资源代谢库，进而建立基于水资源竞争的毒杂草与可食牧草种间竞争模型.同时加入入侵扩散作用，建立基于水资源竞争的毒杂草入侵扩散模型，并且运用微分方程稳定性理论对该模型进行稳定性分析.研究表明：在入侵扩散作用下，毒杂草与可食牧草的共存平衡点由一个增加为两个，增加了共存的可能性.

入侵； 稳定性；元胞自动机

生物入侵是指生物由原分布区域经由自然的或人为的途径扩展到一个新的区域，繁殖并维持下去.近现代以来，我国遭受生物入侵的损失比较严重，每年损失数千亿元，尤其是入侵性植物对我国草原生态环境造成了很大的危害.毒杂草的入侵会破坏天然草场的生态平衡，从而使得可食牧草的生长状况恶化或者灭绝，这样就会进一步影响农牧业的发展，而这是所有牧民不想看到的结果[1-5].因此，必须保护农业生态环境发展的良好社会经济环境.

鉴于以上情况，对生物种群的分布状况和数量或密度的研究，在生物数学的研究领域中有着极其重要的意义.然而由于生物种群之间各种复杂的关系制约，要想获得种群在特定时刻的准确分布情况和数量或密度值，往往比较困难，甚至没有完成的可能.因此，对与其等效的稳定状态进行研究，就有着非常重要的理论与应用价值[3-6].

由于我国干旱缺水，并且水资源短缺.所以，怎样更加合理的利用水资源，并且使其更好的为我国的经济发展服务便成为了亟待解决问题[7-8].为此，国内外很多学者对我国的水资源利用效率问题进行了深入的研究[9-13].这些研究为解决我国水资源短缺、水质污染严重等等水资源环境问题提供了帮助.

直至19世纪后期，科学家还在使用简单的挖掘采样方法对植物根系进行研究，这令人难以相信[14].近些年来随着科学技术的发以及人们对根系研究的不断深入,使得根系的研究方法有了很大的改进,特别是Matlab等计算机技术的使用，使根系的定量化研究有了极大的发展[14].众所周知，根系不仅是植物固定和机械支撑的器官，同时，根系在水分和养分吸收、同化物分配方面也是至关重要的.直到20世纪70年代以后，随着人们对生物地球循环过程的不断探索和认知，科学家对自然生态系统中植物根系的研究开始慢慢起步，对生物量的测定才逐渐进入人们的视线[16].植物活性根的分布模式在决定最佳株行距、最佳配置模式及施肥方式方面具有重要的意义[17].植物细根的水平和垂直分布范围是植物营养能力的最基本体现,同时决定着根系对地下资源(水肥)的利用效果.根系生物量的分布格局直接反映了树种根系的分布特点,同时也间接反映了根系在土层中吸收水养分的土层[18].

以干旱地区为背景，该地区日照充足，水分为限制植物生长的关键因素，而植物汲取水分的主要器官为根系，其分布范围决定了个体植物资源代谢库的大小.本文考虑到根系的分布范围，拟引入水资源代谢库，进而建立基于水资源竞争的毒杂草与可食牧草种间竞争模型.同时加入扩散作用，建立基于水资源竞争的毒杂草入侵扩散模型.运用微分方程稳定性理论对该模型进行稳定性分析.

1 基于水资源竞争的毒杂草与可食牧草种间竞争模型的建立

建立毒杂草与可食牧草为水分竞争的个体生长方程，两物种的生长是logistic增长.

(1)

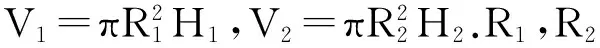
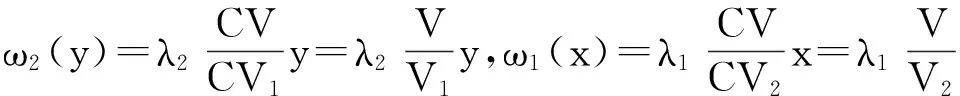
把ω1(x)和ω2(y)代入竞争方程：

(2)

将模型改写为：

(3)

将模型(2)线性化，计算其对应的线性系统，系数矩阵A为：

令:

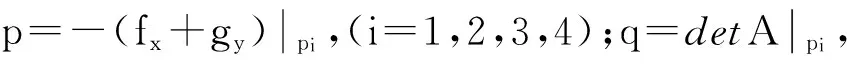
由文献[22]可知，根据特征方程的系数p,q的正负很容易判断平衡点的稳定性，若p>0,q>0则平衡点稳定，则这4个平衡点的稳定性分析见表1.

表1 种群竞争模型的平衡点及稳定性 Tab.1 Equilibrium point and stability of population competition model

2 基于水资源竞争的毒杂草入侵空间扩散模型

在本文中，考虑毒杂草是外来物种，在生长过程中会从密度高的斑块向密度低的斑块发生迁移，因此将单一斑块的毒杂草与可食牧草扩展的相互竞争扩展到二维网格平面，建立了毒杂草入侵空间扩散模型.如果将本节模型(2)考虑成两植物在单个斑块中将产生竞争，同时物种在生长过程中会从密度高的斑块向密度低的斑块发生迁移，引入扩散项，建立斑块间物种入侵空间扩散模型，则模型具有如下形式:

(4)

其中:r1>0，r2>0，α>0，β>0，0<λ1<1，0<λ2<1.模型(4)为第(i,j)个斑块毒杂草入侵空间扩散模型，本模型中元胞自动机设计采用冯诺依曼型，每个元胞有4个邻体.yi,j为二维网格中第(i,j)个斑块的生物量，该斑块的邻体斑块生物量为yi-1,j(上邻体)，yi+1,j(下邻体)，yi,j-1(左邻体)，yi,j+1(右邻体).

同理，考虑外来植物物种从生物量高的斑块向生物量低的斑块发生入侵扩散，第(i,j)个斑块与邻体斑块的生物量差为yi-1,j-yi,j(以上邻体为例).模型中(∑yi±1,j±1-4yi,j)项体现了第(i,j)个斑块中毒杂草的邻体对第(i,j)个斑块的入侵扩散作用，μ为扩散系数[24-25].

3 基于水资源竞争的毒杂草空间扩散模型的稳定性分析

研究与模型等效的稳定状态的数量或密度关系,具有重要的理论与应用价值.

对于模型(4)，其平衡点有4个，如下:

P1(0,θ1)，P2(0,θ2)，p3(K1(1-δ1θ3),θ3)，p4(K1(1-δ1θ4),θ4).

其中:

令扩散项μ(∑N2i±1,j±1-4N2i,j)为参数M.

定理1对模型(4)对应的自治系统，

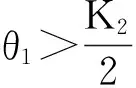
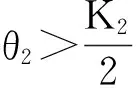
平衡点p3(K1(1-δ1θ3),θ3)的稳定条件为：

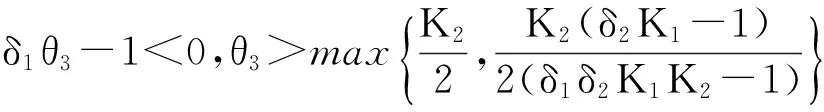
平衡点p4(K1(1-δ1θ4),θ4)的稳定条件为：

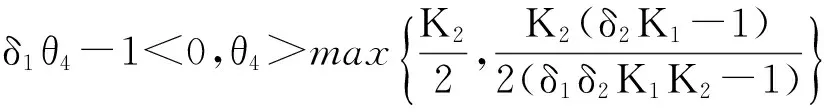
证明对于基于水资源竞争的毒杂草空间扩散模型，可以用近似线性方法判断其平衡点的稳定性.在下面的证明中为简化符号，xi,j均记为X，yi,j均记为Y.

1)对于平衡点p1(0,θ1)，

模型(4)对应的近似线性方程为：

由于:

所以：

则线性方程为：

系数矩阵为：

特征方程系数为：

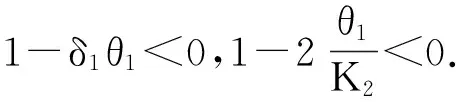
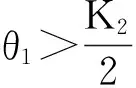
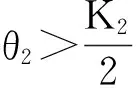
3)对于平衡点p3(K1(1-δ1θ3),θ3)，

模型(4)对应的近似线性方程为：

由于:

所以：

则线性方程为：

系数矩阵为：

特征方程系数为：

再由1-δ1θ3>0及q>0得:

2θ3-K2+δ2K1K2-2δ1δ2K1K2θ3>0，

即：

4 结论

在以上两个模型中，模型(2)是毒杂草与可食牧草的水资源竞争模型，该模型只考虑了当两个种群在同一个水资源环境中生存时它们的相互竞争关系.而模型(4)是基于水资源竞争的毒杂草入侵空间扩散模型，该模型考虑到了毒杂草和可食牧草作为两个物种在单个斑块中将产生竞争，而且毒杂草是外来物种，在生长过程中会从密度高的斑块向密度低的斑块发生迁移这一重要因素.可以说模型(4)是模型(2)的改进.所得到的结果中：没有加入扩散项时，模型(1)的4个平衡点包括零平衡点和毒杂草灭绝的平衡点以及一个共存的非零平衡点；加入扩散项之后，模型的零平衡点和毒杂草灭绝的平衡点消失，而且毒杂草与可食牧草的共存的非零平衡点由一个变为两个.说明在扩散作用下，两种群的可能出现两种稳定情况，而且毒杂草续存的可能性增加.

[1] ANDERSON RM,MAY RM.The invasion,persistence and spread of infectious diseases within animal and plant communities[J].Philos Trans R Soc Lond B Biol Sci. 1986 Dec 15;314(1167):533-570.

[2] 安志兰,郭笃发,褚栋,等.生物入侵对我国生态环境的影响及其控制策略[J].山东农业科学,2007(1):87-91.

[3] 齐相贞,林振山,刘会玉.竞争和景观格局相互作用对外来入侵物种传播影响的动态模拟[J].生态学报,2016,36(3):569-579.

[4] 张靖梓,柏新富,侯玉平,等.山东半岛沿海防护林入侵植物美洲商陆及其伴生种生长竞争力的比较[J].林业科学,2016,52(3):23-29.

[5] 刘伟,杨震,晏娟.生物入侵的危害与防治措施[J].安徽农业科学,2015,43(26):104-107.

[6] 毛凯,李日华.种群竞争模型的稳定性分析[J].生物数学学报,1999(3):288-292.

[7] 张娜,谢斌锋,苏倩倩,等.具有毒素和捕获作用的两种群竞争系统的稳定性分析[J].数学的实践与认识,2012,42(18):117-125.

[8] 周雪.具有Logistic增长项的两种群竞争Keller-Segel模型的稳定性分析[J].哈尔滨师范大学自然科学学报,2015,31(3):28-29.

[9] 赵晨,王远,谷学明,等.基于数据包络分析的江苏省水资源利用效率[J].生态学报,2013,33(5):1636-1644.

[10] 马文静,王晓燕,耿润哲.我国森林生态系统水量调节研究综述[J].首都师范大学学报(自然科学版),2016,37(2):87-92.

[11] BO L,YU L,DI X U,et al.Advances in evaluation study on utility of agriculture water utilization[J]. Shuikexue Jinzhan/advances in Water Science,2009,20(5):732-738.

[12] LIU Y,DU J,ZHANG J B.Estimation on utilization efficiency of agricultural water resource in Hubei Province[J].China Population,Resources and Environment,2007,17(6):60-65.

[13] QIAN W J,HE C F.China′s regional difference of water resource use efficiency and influencing factors[J].China Population,Resources and Environment,2011,21(2):54-60.

[14] ZHANG S Q,ZHANG X,YU L X.The evaluation system water use efficiency and effective[J].Modern Property Management,2011,10(2):89-91.

[15] JI Y H,ZHANG H W,JIANG L.Water efficiency evaluation of Lanzhou based on data envelopment analysis[J].Resources & Industries,2012,14(1):49-52.

[16] BOHM W.Methods of Studying Root Systems[M].Berlin:Spring-erlag,1979.

[17] 宇万太,于永强.植物地下生物量研究进展[J].应用生态学报,2001,12(6):927-932.

[18] 黄建辉,韩兴国,陈灵芝.森林生态系统根系生物量研究进展[J].生态学报,1999(2):270-277.

[19] SCHROTH G.Tree root characteristics as criteria for species selection and systems design in agroforestry[J].Agroforestry Systems,1995,30(1/2):125-143.

[20] 张宇清,朱清科,齐实,等.梯田埂坎立地植物根系分布特征及其对土壤水分的影响[J].生态学报,2005,25(3):500-506.

[21] 徐彩琳.植物种内与种间竞争的计算机模拟实验研究[D].兰州：兰州大学,2000:24-27.

[22] XU R,CHAPLAIN M A J,DAVIDSON F A.Persistence and global stability of a ratio-dependent predator-prey model with stage structure[J].Applied Mathematics & Computation,2004,158(3):729-744.

[23] 姜启源,谢金星,叶俊.数学模型[M].4版.北京:高等教育出版社,2010:223-246.

[24] TAKEUCHI Y.Diffusion-mediated persistence in two-species competition Lotka-Volterra model[J].Mathematical Biosciences,1989,95(1):65-83.

[25] ZHANG X A,CHEN L.The linear and nonlinear diffusion of the competitive Lotka-Volterra model[J].Nonlinear Analysis,2007,66(12):2767-2776.

责任编辑：时 凌

The Stability Analysis of Poisonous Weeds′ Invasion Model
Based on the Competition of Water Resources

SHI Lei1，LIU Hua1*,JIANG Rui1,WEI Yumei2

(1.School of Mathematics and Computer Science, Northwest University for Nationalities,Lanzhou 730030,China;2.Experimental Center,Northwest University for Nationalities,Lanzhou 730030,China)

This paper takes the competitive environment as the background of plants for water in arid regions.Considering the range of root system distribution,we can build the water metabolic warehouse,then build the inter-species competition model of poisonous weeds,and edible grass based on competition of water resources.At the same time,to join the invasion of diffusion,we build the diffusion model of poisonous weeds′ invasion based on water resources competition,and then analyse its stability by using the stability theory of the ordinary differeatial equations. Research shows that under the influence of the invasion and diffusion,the coexistence equilibrium points of the poisonous weeds and the edible grass could be increased to two,which increased the possibility of coexistence.

invasion；stability；cellular automata

2016-11-15.

国家自然科学基金项目(31260098)；国家民委中青年英才计划项目(〔2014〕121号)；西北民族大学研究生科研创新项目(Yxm2016124)；2013年西北民族大学创新团队资助项目.

石磊(1989- )，男，硕士生，主要从事经济系统与生态系统分析的研究；*

刘华(1977- )，男(回族)，教授，主要从事生态数学及计算机模拟的研究.

1008-8423(2016)04-0365-06

10.13501/j.cnki.42-1569/n.2016.12.002

O29

A