改进灰色GM(1,1)模型在滑坡预测中的应用
2017-01-13王旭昭白梦洁
王旭昭,侯 磊,苏 龙*,白梦洁
(1.湖南农业大学 资源环境学院,湖南 长沙 410128;2.湖南农业大学 东方科技学院,湖南 长沙 410128)
改进灰色GM(1,1)模型在滑坡预测中的应用
王旭昭1,侯 磊2,苏 龙1*,白梦洁1
(1.湖南农业大学 资源环境学院,湖南 长沙 410128;2.湖南农业大学 东方科技学院,湖南 长沙 410128)

滑坡形成因素复杂,具有典型的灰色不确定性。为研究滑坡发展趋势,在已有滑坡预测技术的基础上,分析了典型灰色GM(1,1)模型在运算过程的误差原因,建立了改进灰色GM(1,1)模型;并运用滑坡实例验证了改进模型,直观显示曲线拟合情况。结果表明,改进后的模型预测精度等级明显提高,相对误差减小;说明所建滑坡预测模型效果好,在滑坡位移预测中有效可行。
灰色理论;改进;GM(1,1)模型;滑坡预测
由于滑坡地质过程、形成条件、诱发因素的复杂性、多样性及其变化的随机性、不稳定性,导致滑坡动态信息难以捕捉。建立滑坡预测模型可以有效减少滑坡灾害对人民生命财产的危害。针对滑坡预测模型,李秀珍[1]、王腾军[2]等通过不同计算方法对传统GM(1,1)模型进行优化,建立的滑坡预测模型精度均有不同程度的提高,但未对传统模型公式的不合理性进行改进;曹洪洋[3]等采用BP神经网络方法和GIS分析技术,建立了群发性降雨型滑坡灾害预测模型;毕华兴[4]、喻根[5]等采用GIS技术建立了滑坡预测模型;贺小黑[6]、周中[7]等对Verhulst模型进行了相关改进,并建立了滑坡预测模型。这些滑坡预测模型的建立为滑坡预测分析提供了重要参考。
大多数滑坡预测模型都是根据灰色预测理论建立的,其中灰色GM(1,1)模型最为常用,其弥补了传统数理统计的不足,对于样本的多少、有无规律均无要求。GM(1,1)模型是一阶单变量微分方程,与利用离散数据所建立的、按时间作逐段分析的、递推的、离散的模型有着本质的区别。GM(1,1)模型不是原始数学模型,而是生成数据序列模型;通过对生成数列的处理,使无规律的原始数据呈现出一定的规律性[8-9];但传统灰色GM(1,1)模型存在预测精度不高的问题。鉴于此,何昕[10]、马维军[11]等分别运用马尔科夫链理论、补充残差和加权平均的方法对灰色GM(1,1)模型进行了改进,并对改进后的模型进行了误差检验;结果表明,改进后的灰色GM(1,1)模型的精度均有所提高,但上述改进并没有针对模型公式本身的不足进行优化。本文通过对模型公式的分析,采用自动寻优定权法及最小二乘法对灰色GM(1,1)模型进行改进,并运用长、短期监测数据(新滩滑坡、黄茨滑坡的监测数据)对改进后的模型进行了实例分析。
1 灰色GM(1,1)模型的建立
基于灰色GM(1,1) 模型的滑坡预测模型是由一个包含单变量的一阶微分方程构成的模型。其建模的实质是对原始数据先进行一次累加生成,使生成的数据序列呈现一定规律,然后通过建立一阶微分方程模型,求得拟合曲线,用以对系统进行预测[11-13]。
滑坡位移原始数列为:
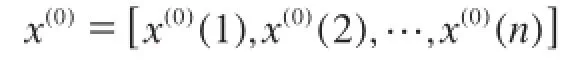
对原始数据进行1-AGO变换,生成一阶累加序列,即
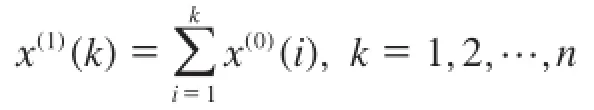
邻均值等权生成序列为:
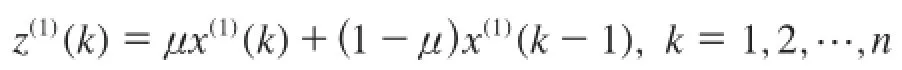
式中,μ为权重系数,μ∈[0,1],一般假定μ=0.5,则有:
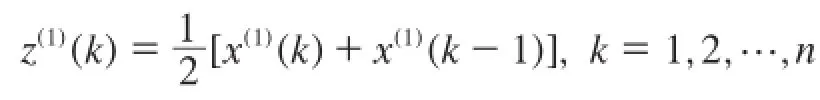
灰色GM(1,1)模型的微分方程为:

式中,a、u为位置参数,运用最小二乘法进行求解,

式中为x(1)序列的预测值;c为待定常数。为求解c,需要事先确定预测初始值,一般假定xˆ(1)(1)=x(0)(1),则有,即

邻均值等权还原序列为:
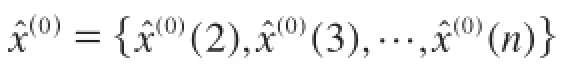
2 灰色GM(1,1)模型精度检验
在实际滑坡预测中,为达到高精度预测,需要对数据进行残差检验以及对滑坡预测模型所用原始数据、预测数据进行后验差检验,只有检验结果符合精度等级要求,才能运用建立的灰色GM(1,1)模型进行滑坡位移的预测。
2.1 残差检验
绝对残差序列计算公式为:e(0)(k)=x(0)(k)-xˆ(0)(k) ;为考察绝对残差大小,计算相对残差;在相对残差基础上,计算平均残差
2.2 后验差检验
1)滑坡原始数据平均值、均方差计算。
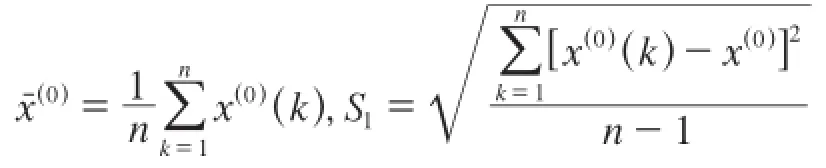
2)绝对残差平均值、均方差计算。

2.3 预测精度等级
灰色关联度检验与残差、后验差检验有着不一致的检验结果[14],不适合灰色GM(1,1)模型的检验,因此不对关联度进行分析。预测精度等级分类见表1[15]。
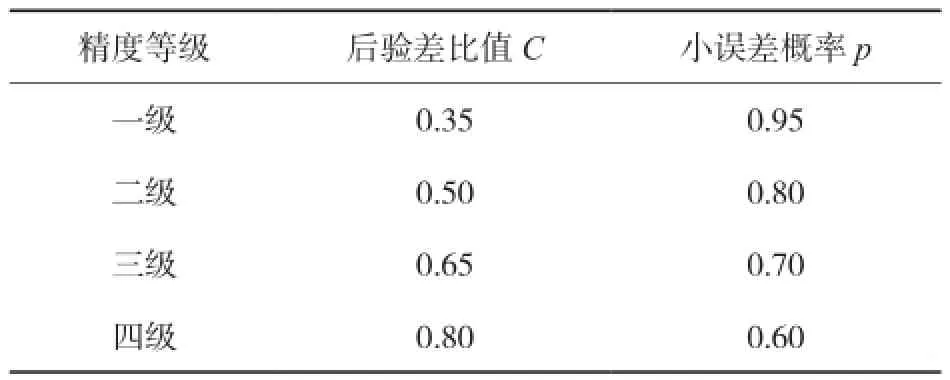
表1 预测精度等级分类
3 模型存在的问题及改进
通过对灰色GM(1,1)模型一般形式的建立,发现其求解过程存在以下两个问题:①对权重系数μ的假设,一般假设μ=0.5,但从理论上无法解释在权重系数为0.5时模型的预测精度最高,故在此需对权重系数的取值进行修正。②对初始值的假设,将x(0)(1)作为求解微分方程的初始值,则预测的曲线拟合必定通过(1,x(0)(1)),但由于模型实质上为外推法,拟合结果应满足平均相对误差最小,因此需要对初始值的选取进行改进。
为解决因假设造成的误差,令初始权重系数μ=0,计算平均相对误差,具体计算公式为:
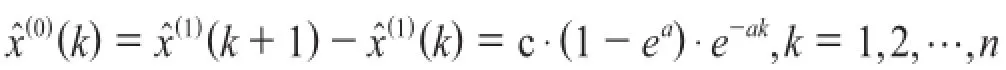
令K=c·(1-ea),则有:
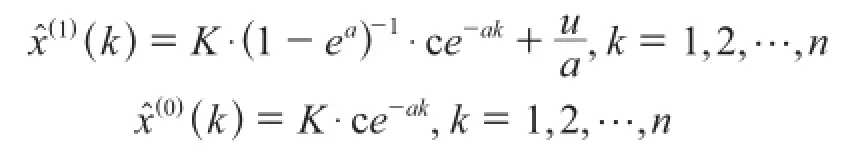
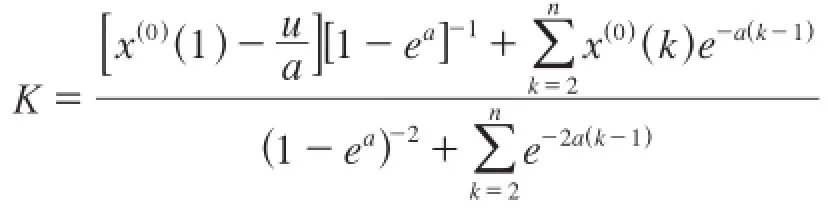
在μ=0的基础上,增加一个微小量Δμ,令μ⇐μ+Δμ,重复至μ=1,取得平均相对误差最小,即模型预测精度最高时的权重系数作为最佳权重,进行预测。
4 应用实例
4.1 新滩滑坡预测
三峡西陵峡中的新滩滑坡发生于1985年6月12 日,滑坡体积约为3 000余万m3,滑坡体前部的土石堵塞了约1/3的长江江面。上段滑体岩土体结构由后缘的纯崩积物组成的单一结构逐渐过渡到前端的上层为崩积物、下层为坡积物的双层结构。新滩滑坡的位移监测于1977 年11 月开始,长期的变形监测为认识和研究滑坡的动态规律提供了丰富的数据和信息[16]。
运用传统灰色GM(1,1)模型与改进灰色GM(1,1)模型分别进行数据处理,改进后的模型取μ=0.373时预测精度最高,平均相对误差随权值变化曲线见图1。模型改进前后预测对比分析数据和该滑坡位移监测值及预测值随时间的变化曲线,见表2和图2。
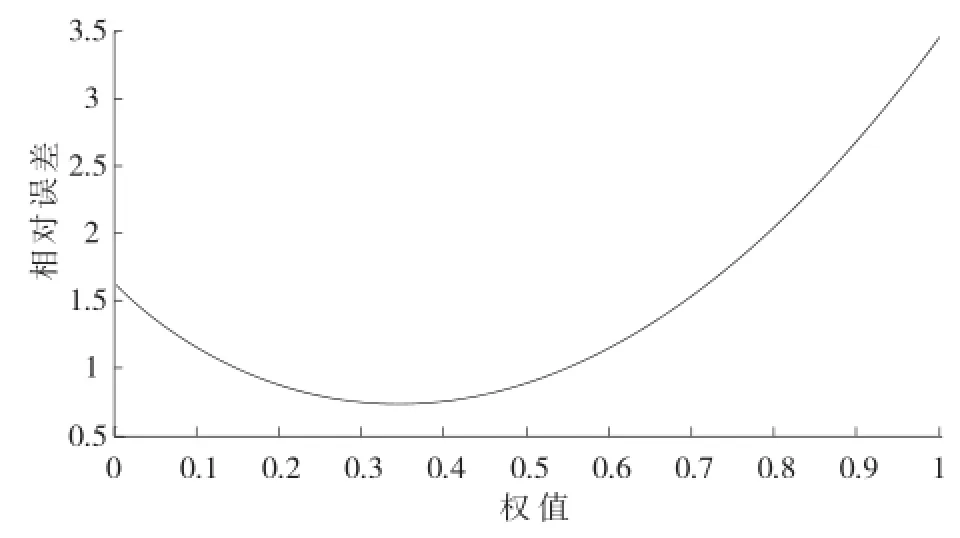
图1 新滩滑坡预测模型平均相对误差随权值变化曲线
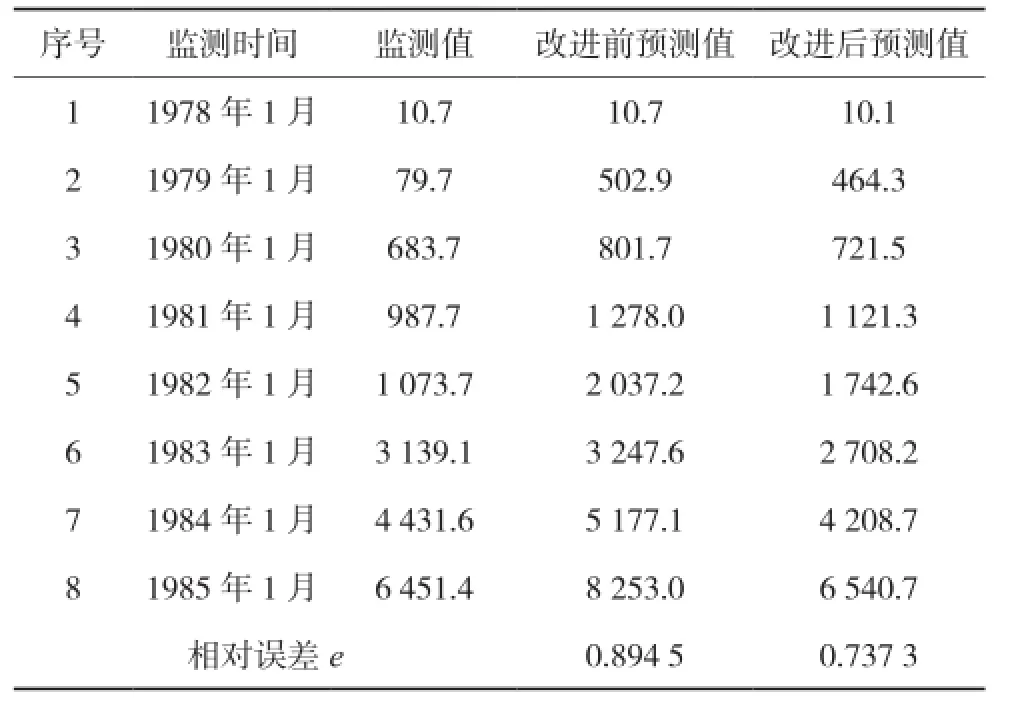
表2 新滩滑坡位移监测值及模型预测值/mm
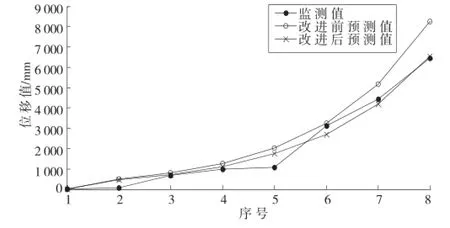
图2 新滩滑坡位移监测值及预测值随时间的变化曲线
综上可知,改进的灰色GM(1,1)模型的相对误差为0.737 3,传统模型的相对误差为0.894 9。改进前后模型预测后验差比值为C1=0.570 9、C2=0.208 9。小概率误差p均为1,根据表1预测精度等级分类,改进前预测精度等级为三级,改进后预测精度等级为一级。
4.2 黄茨滑坡预测
甘肃省永靖县黄茨滑坡起始监测时刻为1994 年8 月1日,监测时间间隔为15 d,滑坡发生时间为1995 年1月30日凌晨2点30分,根据黄茨滑坡A6号监测点的地面位移信息资料[17],改进后模型取μ=0.434时预测精度最高,平均相对误差随权值变化曲线见图3,模型改进前后预测对比分析数据和该滑坡位移监测值及预测值随时间的变化曲线,见表3和图4。
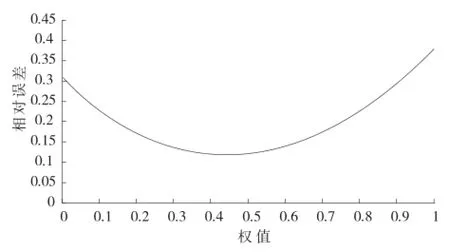
图3 黄茨滑坡预测模型平均相对误差随权值变化曲线
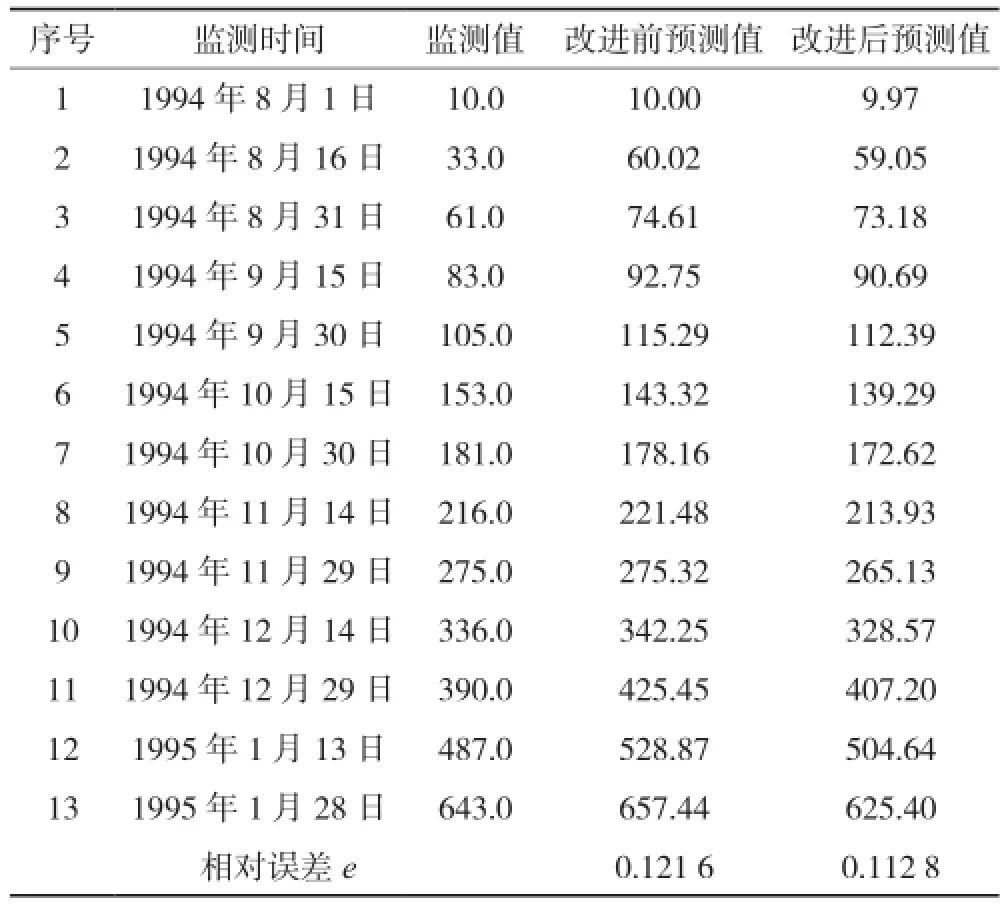
表3 黄茨滑坡位移监测值及模型预测值/mm
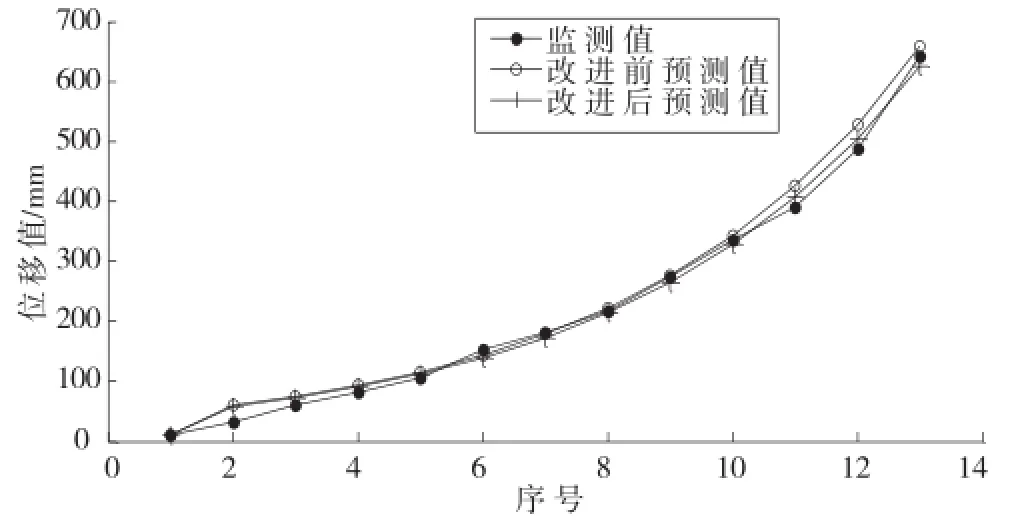
图4 黄茨滑坡位移监测值及预测值随时间的变化曲线
综上可知,改进的灰色GM(1,1)模型相对误差为
0.112 8,传统模型相对误差为0.121 6。改进前后模型预测后验差比值为C1=0.159 1、C2=0.102 6;改进滑坡灰色GM(1,1)模型精度均有提高。
从图2、4中可以看出,改进后的灰色GM(1,1)模型的预测曲线更接近于原始数据的曲线,特别是对于数值波动比较大的数据,改进后的模型预测效果和精度明显提高。从拟合效果和预测精度可看出,改进模型在滑坡预测上合理可行。
5 结 语
1) 本文通过对传统灰色GM(1,1)模型公式的分析,运用最小二乘法和自动寻优定权的方法对预测初始值及权重μ进行了改进,极大地提高了灰色模型的预测精确度。
2)通过实例验证,改进后的灰色GM(1,1)模型具有对预测过程进行优化的能力,能使长期滑坡预测的精度得到显著提高,也同样适用于短期滑坡预测,在理论与实际应用中均切实可行。
[1] 李秀珍,孔纪名,王成华.灰色GM(1,1)残差修正模型在滑坡预测中的对比应用[J].山地学报,2007,25(6):741-746
[2] 王腾军,赖百炼,叶俊华,等.基于GM(1,1)数据融合算法的滑坡预测研究[J].测绘通报,2012(5):63-65
[3] 曹洪洋,王禹,满兵.基于GIS的区域群发性降雨型滑坡时空预报研究[J].地理与地理信息科学,2015,31(1):106-109,124 [4] 毕华兴,中北理,阿部和时.GIS支持下的滑坡空间预测与危险等级划分[J].自然灾害学报,2004,13(3):50-57
[5] 喻根,B H P Maathuis,C J van Westen.基于GIS的滑坡预测模型的预测率及其作用[J].岩石力学与工程学报,2007,26(2):285-291
[6] 贺小黑,王思敬,肖锐铧,等.Verhulst滑坡预测预报模型的改进及其应用[J].岩土力学,2013,34(增刊1):355-364
[7] 周中,刘宝琛.滑坡预测预报的Verhulst反函数残差修正模型[J].中国铁道科学,2009,30(4):13-18
[8] 仇环,曲国庆,苏晓庆.GM(1,1)模型的改进[J].山东理工大学学报(自然科学版),2008,22(2):5-8
[9] 刘思峰,郭天榜.灰色系统理论及其应用[M].北京:科学出版社,1999
[10] 何昕,陈亚青.应用改进的灰色模型预测民航管制员数量[J].实验科学与技术,2010,8(1):28-30
[11] 马维军.基于改进的灰色GM(1,1)模型预测产品的故障数[J].黑龙江大学自然科学学报,2005,22(3):389-392
[12] 樊新海,苗卿敏,王华民.灰色预测GM(1,1)模型及其改进与应用[J].装甲兵工程学院学报,2003,17(2):21-23
[13] 张大海,江世芳,史开泉.灰色预测公式的理论缺陷及改进[J].系统工程理论与实践,2002,22(8):140-142
[14] 吴涛,李必强,钱正芳.GM(1,1)模型的关联度检验分析[J].武汉理工大学学报,2002,24(6):85-87
[15] 肖新平,宋中民,李峰.灰技术基础及其应用[M].北京:科学出版社,2005
[16] 周斌.新滩滑坡预测预报分析[J].路基工程,2012(4):182-185 [17] 王念秦.黄土滑坡预报研究[D].西安:西北大学,2000
P258
:B
:1672-4623(2016)11-0088-03
10.3969/j.issn.1672-4623.2016.11.031
王旭昭,主要从事工程灾害防治、安全管理与评价方面研究。
2015-07-22。
项目来源:2015年度湖南农业大学大学生科技创新基金资助项目(ZK15015);2015年度湖南农业大学大学生创新性实验计划资助项目(XCX15116);湖南农业大学杨仁斌科学基金资助项目(DS0408)。
(*为通讯作者)
