基于离散沉降观测的城市地面沉降监测

井 研，胡庆武，艾明耀，宋晓光

（1.武汉大学 遥感信息工程学院，湖北 武汉 430030）

基于离散沉降观测的城市地面沉降监测

井 研1，胡庆武1，艾明耀1，宋晓光1

（1.武汉大学 遥感信息工程学院，湖北 武汉 430030）

由于离散观测点沉降数据无法全面反映城市沉降状况，探讨了利用大量离散观测点沉降观测数据进行城市地面沉降监测的方法。设计了利用大量沉降观测数据进行空间插值计算的城市地面沉降监测技术流程；提出了基于交叉验证的城市地面沉降空间内插模型的选取方法；并以某县级市为例，利用该方法对城市地面沉降进行了计算和可视化。结果表明，该方法有效可行，操作性高，具有广泛的应用前景。

地面沉降；监测；空间插值；交叉验证；等值线

目前，在我国19个省份中有超过50个城市发生了不同程度的地面沉降，累计沉降量超过200 mm的总面积超过7.9万km2。地面沉降的重灾区主要是长江三角洲地区、华北平原和汾渭盆地，其中长江三角洲地区近30 a累计沉降超过200 mm的面积近1万km2，占区域总面积的1/3。地面沉降不但会使水患加剧，引起其他地质灾害，而且对社会的稳定发展与国民财产安全存在巨大威胁[1-2]。为了有效控制城市地面沉降和减少沉降造成的影响，城市规划、地质等管理部门需要了解和掌握城市地面沉降情况，同时为城市规划和建设发展提供重要的科学依据。

现今国内的监测手段主要有水准测量、三角高程测量、数字摄影测量、InSAR、GPS、监测标、地下水动态监测等，但数字摄影测量、InSAR等大面积区域监测手段观测技术相对不够成熟，成本也高，因此很多部门在城市监测中还是以使用水准测量、GPS等单点测量为主，获取离散观测点沉降数据。由于观测站点个数受到限制，获取的观测资料只能反映局部沉降监测信息，无法从整体上对观测区进行监测。为了弥补这一不足，近年来，Kriging法等空间插值方法在城市地面沉降观测中得到较多应用，但由于不同的空间插值方法具有各自的特点，且沉降情况的时空变异较大，导致不同空间插值方法在不同实验区中表现出不同的适用性，故选择适当的空间插值方法进行格网化是离散沉降观测地面监测的关键。本文设计了利用大量离散沉降观测数据进行城市地面沉降空间内插计算的流程，并提出了基于交叉验证的城市地面沉降空间内插模型的选择方法。最后，以某县级市为例，采用该方法对城市地面沉降进行计算和可视化。

1 基于空间插值的城市沉降监测方法

在城市沉降监测中，常用的单点测量手段获取的单站观测数据是离散的、单一的、不能反映整个城市的沉降情况，为此，针对获取的离散观测数据，本文基于空间插值方法实现覆盖整个城市的沉降计算，并选择沉降等值线作为反映整个城市沉降变化情况的可视化方式。目前存在多种空间插值方法，每一种方法都有各自的优缺点，且不同实验区沉降情况的时空变异较大，致使不同空间插值方法在不同的实验区表现出不同的适用性，因此，本文提出的空间插值城市沉降计算和监测方法的技术流程如图1所示。

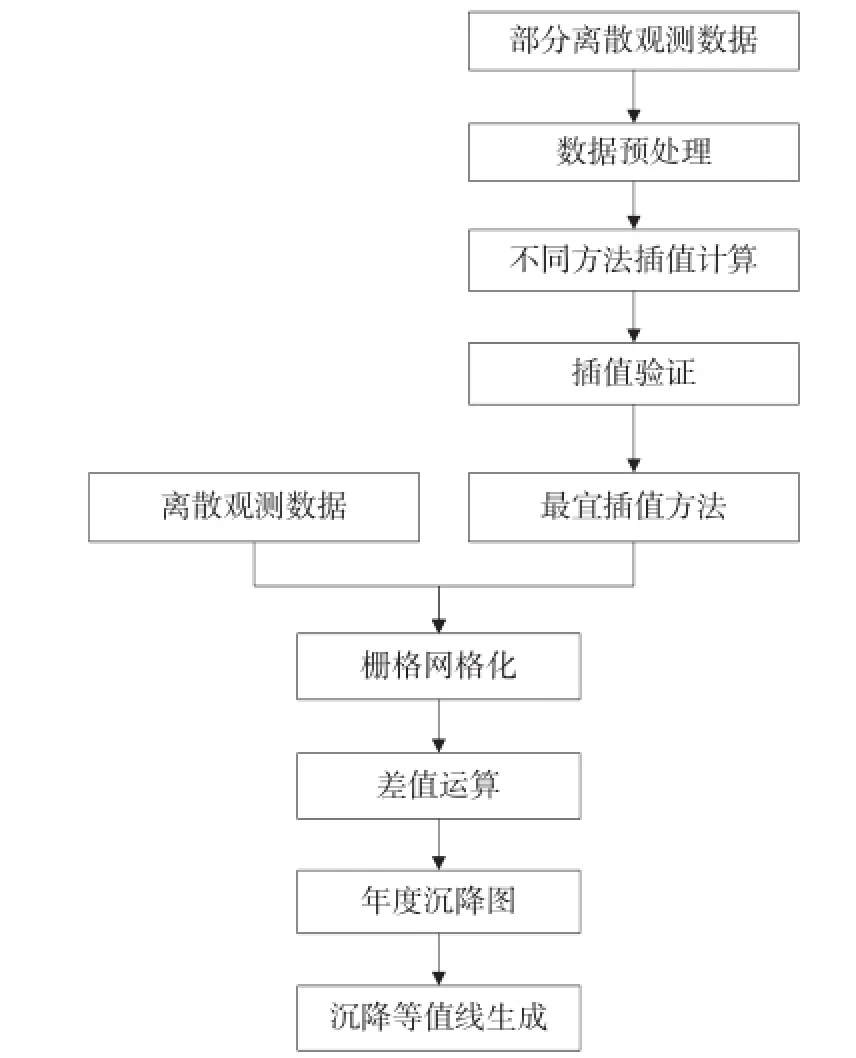
图1 空间插值城市沉降监测方法技术流程图

首先采用不同空间插值方法，对某一年份离散的沉降点高程记录数据进行插值网格化，并通过插值验证方法获得该实验区的最宜插值方法；然后运用该插值方法对两个不同年份的高程记录数据进行插值网格化、差值运算，得到城市地面年度沉降图；最后利用年度沉降图生成沉降等值线专题图，为城市地面沉降预测、预防和应急提供直观的数据。

2 空间插值模型及交叉验证

IDW法、Kriging和样条函数为3种常见的空间插值方法[3]。对于不同的观测点分布、不同的地形环境和观测数据量，它们插值计算的结果在一定范围内存在差异。本文将空间插值计算结果与实测点位沉降观测数据进行对比交叉验证，从而选取最适宜的空间插值方法。

2.1 3种空间插值模型及比较

IDW插值把估算值和实测点间的距离作为权重因子，权重值为距离反比[4-5]，公式为：

式中，zi为估算点的数值；Z0为插值要素在第i点的实测值；n为参与插值计算的实测点数量；λi为各采样点权重，其计算公式为：

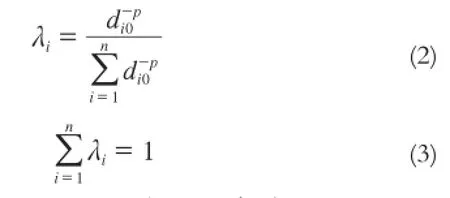
式中，di0-p是第i个预测点和各已知采样点的距离；p为幂指数，一般取值在0.5～3。随着幂值的增大，内插值将逐渐接近最近采样点的值。

Kriging插值是通过一组具有z值的分散点生成估计表面的高级地统计过程[6-7]。其假定采样点之间的距离或方向可用于说明表面变化的空间相关性。ArcGIS提供的Kriging法工具可将数学函数与指定数量点或指定半径内的所有点进行拟合，以确定每个位置的输出值。

样条函数插值是通过控制估计方差，利用一些特征节点，用多项式拟合的方法来产生平滑的插值曲线[8-10]，公式为：

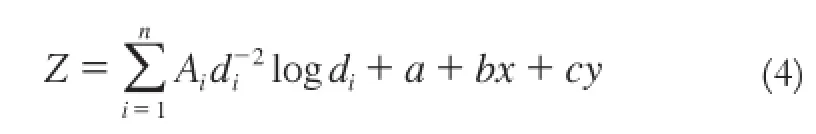
式中，Z为待估计高程栅格值；di为插值点到第i个观测站点的距离；a+bx+cy为高程的局部趋势函数，x、y为插值点的地理坐标；为一个基础函数，通过它可以获得最小化表面的曲率；Ai、a、b和c为方程系数；n为用于插值的观测站点的数目。

在城市地面沉降插值计算时，3种空间插值模型的特点如表1所示。

表1 3种空间插值模型比较

2.2 空间插值交叉验证

如图2所示，首先假定某些观测点高程值未知，通过周围站点实测值插值来估算，然后计算验证站点的实测值与估算值之间的误差值。被估算高程值的站点称为验证站点，用于插值的站点称为采样站点。产生这种误差有两方面原因：插值算法的准确性和参与插值的站点的疏密程度[11-12]。虽然完全区分两种原因造成的误差十分困难，但对不同的插值方法，交叉验证仍可准确验证不同插值方法之间的相对精度。

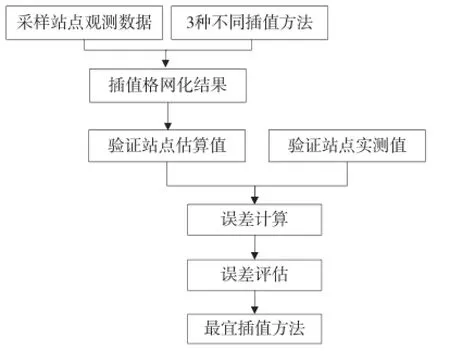
图2 交叉验证流程图

本文采用平均绝对误差（MAE）和平均误差平方的平方根（RMSIE）作为3种插值方法精度评估标准，公式为：

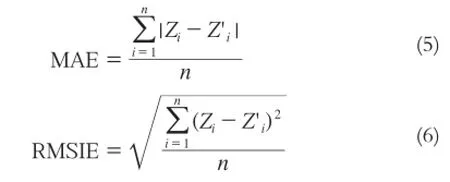
式中，Zi为第i个站点的实际观测值；Zi'为第i个站点的插值预测值；n为参与验证的站点数目。MAE可评估估算值可能的误差范围，更好地反映估算值误差实际情况；RMSIE可反映利用样点的估算灵敏度和极值效应，值越小，表明估算值与实测值越接近，精度越高。采用这两种评估标准能很好反映不同插值方法的相对精度，以此选择最适宜的空间插值方法进行城市沉降计算。

3 实验分析

3.1 实验区域及数据介绍

本文以我国东部某县为研究区域，采用的数据源为：63个沉降站点的位置数据和属性数据，坐标用经纬度表示的，属性数据主要包括编码、名称等；沉降站点在2009年和2010年的高程记录观测数据，每条记录包括沉降站点的编码、名称、高程值、观测条件等，其分布如图3所示。

图3 沉降观测点分布图

3.2 空间插值交叉验证结果分析

本文首先从63个沉降观测站点中选择8个观测站点作为验证站点，其他作为采样站点；然后将IDW法、Kriging法、样条函数法分别应用于采样站点格网化，并通过误差评估，最后获取最适合实验区的插值方法。3种空间插值结果如图4所示。

由图4中可知，使用IDW法、Kriging法和样条函数法栅格化所得出的实验区高程分别集中在1.052～5.165 m、1.052～5.155 m、0.650～5.626 m之间。通过数据可以看出，实验区地势大致平坦，和实际情况相符。表2为3种空间插值方法交叉验证结果。

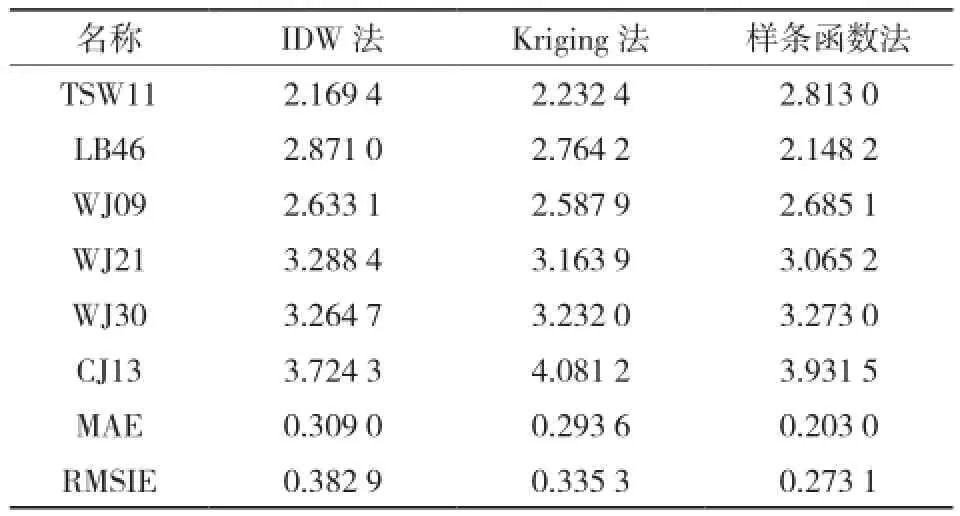
表2 空间插值交叉验证结果/m

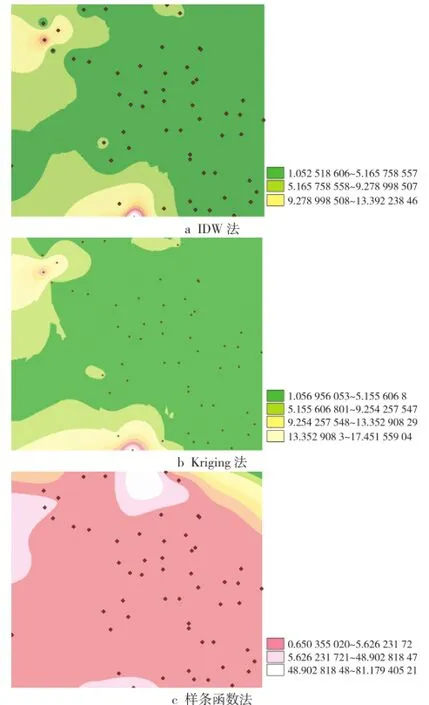
图4 3种方法的插值结果

IDW法、Kriging法和样条函数法对2009年高程观测数据交叉验证结果表明，样条函数法最优，Kriging法次之。在实验区中使用样条函数法进行高程记录栅格化，空间栅格化精度要高于使用IDW法和Kriging法结果。

3.3 空间插值沉降监测结果分析

针对实验区的离散沉降数据，根据交叉验证选择样条函数法进行空间插值计算，得到整个城市范围内沉降监测结果，以等值线图表示，如图5。

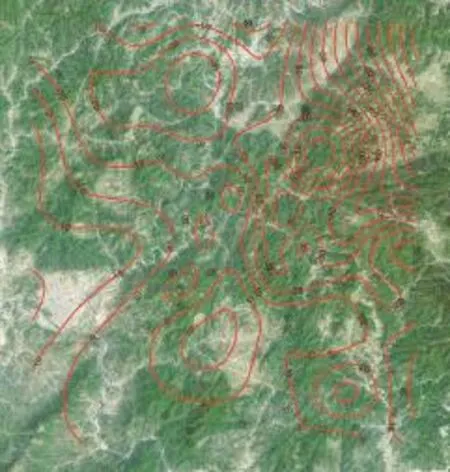
图5 沉降等值线图（单位：mm，间隔10 mm）

图5中，负值表示地面有沉降，0值表示地面不升不降，正值表示地面有抬高。实验区在2009～2010年期间普遍具有地面下沉趋势，且从西至东来看，地面下沉现象越来越明显，尤其是该区域的东北部地面下降更为显著，最大沉降可达1 m左右。城市区域的西南部有地面抬高趋势，并呈漏斗状，而北部普遍具有下沉趋势。另外，从等值线的疏密可以看出，城市的西部沉降变化比较平缓，东部沉降变化坡度较大。从城市沉降等值线专题图上可以很容易地获取和掌握城市的沉降分布情况，从而为地质、城市规划等部门决策提供进一步支持。

4 结 语

本文将空间插值技术引入到城市沉降定量研究中，通过交叉验证分析选择样条函数法进行实验区沉降空间的插值计算，并在此基础上制作了城市地面沉降等值线图，实现了从点状的沉降观测值到覆盖整个城市的地面沉降可视化，能够直观有效地表达地面沉降变化。它从空间上反映了地面沉降监测结果，操作性强，具有很好的实用性；今后还需要进一步研究沉降插值异常分析方法，以获取更为可靠的城市地面沉降监测结果。

[1] 王伟.抽取地下水引起的地面沉降可视化研究[D].南京：河海大学,2006

[2] 侯卫生,吴信才,刘修国.基于GIS的城市地面沉降信息管理与预测系统研究[J].岩土力学,2008,29(6)：1 685-1 690

[3] 吴文玉,马晓群.基于GIS的安徽省气温数据栅格化方法研究[J].中国农学通报,2009,25(2)：263-267

[4] 李新,程国栋,卢玲.空间内插方法比较[J].地球科学进展,2000,15(3)：260-265

[5] 石朋,芮孝芳.降雨空间插值方法的比较与改进[J].河海大学学报(自然科学版),2005,33(4)：361-365

[6] 李军,游松财, 黄敬峰.中国1961～2000年月平均气温空间插值方法与空间分布[J].生态环境,2006,15(1)：109-114

[7] 陈欢欢,李星,丁文秀.Surfer 8.0等值线绘制中的十二种插值方法[J].工程地球物理学报,2007,4(1)：52-57

[8] 黄杏元,马劲松,汤勤.地理信息系统概论[M].北京：高等教育出版社,2001

[9] 鲁振宇,杨太保,郭万钦.降水空间插值方法应用研究：以黄河源区为例[J].兰州大学学报(自然科学版),2006,42(4)：11-14 [10] 李军龙,张剑,张丛,等.气象要素空间插值方法的比较分析[J].草业科学,2006,23(8)：6-11

[11] 许云,龙步菊,潘学标,等.河北地区气温内插模型及检验方法[J].气象与环境学报,2010,26(2)：27-30

[12] 潘耀忠,龚道溢,邓磊,等.基于DEM的中国陆地多年平均温度插值方法[J].地理学报,2004,59(3)：366-374

P258

：B

：1672-4623（2016）11-0084-04

10.3969/j.issn.1672-4623.2016.11.030

井研，硕士研究生，研究方向为地图学与地理信息系统。

2015-09-29。

项目来源：国家重点基础研究发展计划资助项目（2010CB732106）。