时间窗约束下的生鲜产品物流配送路径优化研究

杨 婷,周建国

(湖南科技大学,湖南 湘潭 411201)

时间窗约束下的生鲜产品物流配送路径优化研究

杨 婷,周建国

(湖南科技大学,湖南 湘潭 411201)

传统的“重生产,轻流通”的思想已经不能满足当前人们对于农产品的要求。选择最优的物流配送路径,对降低流通成本、促进农产品流通等具有重大意义。文章通过构建客户满意度函数和物流成本函数对时间窗条件下的生鲜产品配送路径进行优化,设计仿真实验、采用单亲遗传算法来求解该问题。实例证明该优化后模型能更好地解决农产品流通过程中的问题,能为农产品物流配送路线研究提供借鉴意义。

农产品物流；时间窗；客户满意度；遗传算法；VRP

1 引 言

随着生活水平的提高,国民对农产品流通环节的重视程度也随之上升。当前国内农产品存在着流通成本过高、客户满意度低等问题。生鲜领域在农产品中占据很大比重,同样存在这些问题,已经成为制约生鲜产品流通的重要因素。本文探讨生鲜产品流通中的现实问题,通过优化后得到最优的配送路径,以最低的成本、客户最满意的服务完成产品的配送。

路径优化问题(VRP)属于组合优化问题,对于这种问题很难精确求解。[1]目前解决这类问题大多数依靠启发式算法,例如,遗传算法、蚁群算法、粒子群算法、模拟退火算法等。国外学者最先开始研究生鲜物流配送问题。Solomon将时间窗与VRP问题结合,为研究生鲜物流配送路径提供借鉴意义；Brito等研究了在不确定时空情况下的冷冻食品VRP问题,并通过软方法求解。王红玲等人以配送时间最短,成本最低为优化目标采用改进粒子群算法求解该问题；向敏[2]等人在电子商务环境下规划生鲜产品配送的网络体系,设计配送路径,减少物流成本。

基于以上文献,各国学者对时间窗约束下的生鲜VRP问题的研究取得了许多成果,但把时间窗约束下客户满意度作为首要约束条件的研究较少。当前社会客户已经成为企业生存发展的战略性资源,企业在任何情况下都不能忽视客户的感受。出于这种考虑,众多企业越发重视客户满意度。本文将生鲜产品配送过程中的成本函数和顾客满意函数相结合,通过案例证明能为研究生鲜产品物流路线问题提供借鉴意义。

2 生鲜产品物流路径优化模型

2.1 模型描述

现假定某区域内的一农产品企业计划从配送中心向L超市配送生鲜产品,每个超市之间有一定距离,配送中心之间也有一定距离。每个超市只有在规定的时间窗(Eti,Lti)内,才可以进行相应的服务,车辆提前到达需要支付等待费用,延迟到达则需要支付大量的延迟费用。每个超市只由一个车辆负责配送,由k辆车负责配送。要在此区域内确定合适的配送路线,使之配送成本最少,所获得客户满意度最大。

2.2 顾客满意度函数

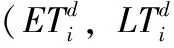
2.3 模型建立

根据上述要求,模型以物流总成本最小为目标,将顾客满意度作为首要约束条件。总成本包括运输费用、等待费用及延迟费用。则最终的总成本模型如下：

S.t：

(1)

(2)

(3)

(4)

(5)

dij：超市之间的距离；i,j:超市的编号；H:单位路程运费率；Mi:各个超市的需求量；C:等待费用；S:等待时间；q:延迟费用；Q:每辆汽车的最大运载量。

若xijk表示车辆k经过超市i,j,则xijk=1,反之则为0。若yik表示车辆k为顾客i服务,则yik=1,反之则为0。

式(1)表示确保平均客户满意度在90%以上；式(2)表示一条路线上汽车所载的货物重量不超过汽车载重量；式(3)～式(5)表示每一个超市只由一辆车运输。

3 时间窗VRP下遗传算法的描述

由于遗传算法(Genetic Algorithm,GA)[4]本身的局限性,如过早“收敛”“早熟”等现象,所以本文借助一种改进的遗传算法进行该VRP问题的求解-单亲遗传算法(PGA)。[5]

3.1 关于遗传算法(GA)与单亲遗传算法(PGA)的比较

(一)遗传算法(GA)在解决VRP问题时,主要通过交叉算子实现整个种群的演变。但在使用序数编码时候,个别问题不能进行交叉操作,交叉操作会使产生的新染色体对应的解不在原问题的解集中。[6]PGA取消了传统遗传算法的交叉操作,代之以仅在一条染色体上进行基因重组等遗传算子,即PGA采用单亲遗传的方式,简化了遗传操作,提高了寻优速度。

(二)GA中主要有选择、交叉、变异等种群进化算子。PGA的种群进化方式主要借助于选择算子,基因重组算子(包括基因换位、基因倒位、基因移位等改变基因顺序算子)和基因突变算子等,PGA中的基因重组实现了GA的交叉和变异功能。PGA的选择算子与GA的选择算子无异。

3.2 编码方案

为了克服二进制编码解决VRP问题的先天性不足,本文采用序数编码,0表示配送中心,1,2,3…表示客户,随机产生一组数表示初始种群。具体编码思路如下：

(1)从左向右累计客户的需求量,一旦累计需求量超过货车的载重量就停止计数,设经过n次累计之后累积量超过货车的载重,则记录此时的断点一为n-1,累积量清零。

(2)从排列的第n位开始继续重复第一步,假设再次累计量超过货车载重量时,此时的累计次数为m,记录此时的断点为n+m-1,累积量清零。

(3)重复以上步骤直至排列的最后一位,生成断点矩阵。

(4)依据断点矩阵,在排列对应位置后面加上0,同时在排列首末位加上0,染色体生成完成。

3.3 适应度函数

适应度函数[7](ft)用于表示当前种群中的个体对于待优化问题的优良性,一般根据目标函数确定。本文选取(ft)=1/(Zmin+V.q)。V为一个很大的正整数,表示惩罚系数,q为延迟费用。

4实例及仿真

结合实际研究课题,在一个区域内随机散布1个配送中心和12个超市(详见表1)。配送采用单一的货车运输。实验中采取以下参数：

汽车装载量为5.5吨,平均车速60km/h,车辆等待费用为每小时20元,延迟费用q=100元。每天最早出发时间为6：00。单位路程运费率H=25,等待费用C=20。惩罚系数V=500。选择概率pc取0.15,单亲遗传算法的最大基因换位次数为6。初始种群个数为20。现要求确定总成本最少、客户最满意的配送方案。

表1 各超市的需求量,服务时间,时间窗

根据上述改进的遗传算法写出C语言程序,在Matlab 2015程序下对该模型进行1000次迭代。仿真得出4条最优的配送路径(见表2)分别为：路径一：0-6-1-7-0；路径二：0-4-10-3-0；路径三：0-12-5-9-11-0；路径四：0-2-8-0。最终系统总成本为19214,客户满意度为93%。与全局最优解较接近。图1表示的模型总成本随迭代次数的寻优过程,图中可以看出遗传算法搜索结果较快,随着进化进行,种群内优良个体逐渐增多,总成本从开始的22000多迅速趋近于全局最优解,并在300代左右开始收敛。说明了算法具有很好的寻优能力。

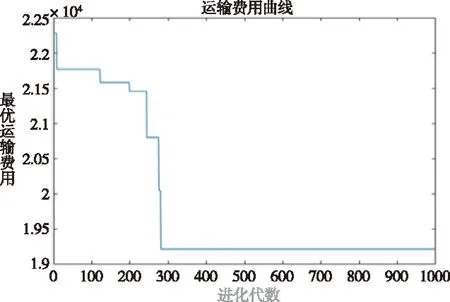
最佳运输费用随迭代次数的进化过程

路径一超市编号6170到达时刻(h)84382932881096630路径二超市编号41030到达时刻(h)83691989221236760

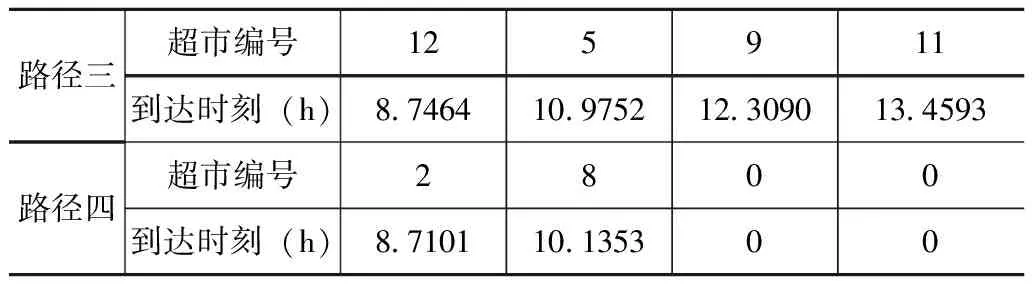
续 表

5 结 论

本文对生鲜产品VRP问题进行了研究,建立了配送总成本模型。基于此类模型求解的复杂性,本文在传统的遗传算法基础上引入单亲遗传算法概念,来寻求配送路径的最佳方案。文中实例分析表明,本文提出的时间窗约束下的生鲜产品配送路径和客户满意度之间的最大平衡,能够满足一定阶段下的农产品企业和客户的现实需求,降低了成本,提高了配送效率,并且使得客户满意度得到最大满足。对于相关企业来说,本文的研究可以为企业带来无形的价值——企业自身形象和企业的经济效益,进而增强企业的竞争力。

[1]罗勇,陈治亚.基于改进遗传算法的物流配送路径优化[J].系统工程,2012(8).

[2]向敏,袁嘉彬,于洁.电子商务环境下鲜活农产品物流配送路径优化研究[J].科技管理研究,2015,35(18).

[3]邓丽君.基于客户满意度的物流配送车辆调度优化模型与算法研究[D].北京：北京交通大学,2012.

[4]J.H.Holland.Adaptation in Natural and Artificial System[M].Cambridge:Mit Press,1975.

[5]李茂军,朱陶业,童调生.单亲遗传算法与传统遗传算法比较研究[J].系统工程,2001,19(1).

[6]梁承姬,黄涛,徐德洪,等.改进遗传算法求解带模糊时间窗冷链配送问题[J].广西大学学报,2016,41(3).

[7]雷英杰,张善文.MATLAB遗传算法工具箱及应用[M].西安：西安电子科技大学出版社,2014.

10.13939/j.cnki.zgsc.2016.49.023