基于遗传算法的汽车平顺性时域仿真与优化

鲍家定++伍建伟++莫秋云

摘 要： 首先，建立汽车五自由度振动系统的力学模型，利用牛顿第二定律建立动力学方程，并基于IFFT法进行路面不平度的时域模拟。然后，通过ADAMS进行对比验证平顺性模型。最后，以悬架刚度阻尼为设计变量，以悬架动挠度和轮胎相对动载荷为约束函数，以座椅中心加权加速度均方根值为目标函数，建立其优化模型，利用Matlab优化工具箱中的遗传算法函数进行优化。优化结果表明，遗传算法具有很强的全局寻优能力，优化结果大大地改善了平顺性指标，提高了汽车的性能。

关键词： 平顺性； IFFT； 时域模拟； Matlab； 遗传算法

中图分类号： TN911.7?34； U461.4 文献标识码： A 文章编号： 1004?373X（2016）23?0136?05

Genetic algorithm based vehicle ride comfort time?domain simulation and optimization

BAO Jiading， WU Jianwei， MO Qiuyun

（School of Mechanical and Electrical Engineering， Guilin University of Electronic Technology， Guilin 541004， China）

Abstract： The mechanical model of vehicle′s five degrees of freedom vibration system was established. The kinetic equation was established with Newton′s second law. The road roughness time?domain simulation was performed based on IFFT （inverse fast Fourier transform） method. The ride comfort model was verified with ADAMS. And its optimization model was established by taking the suspension stiffness and damping as the design variables， suspension dynamic deflection and relative dyna?mic load of vehicle tire as the constraint function， and root?mean?square value of seat center weighed acceleration as the objective function. The model was optimized with genetic algorithm function in Matlab optimization toolbox. The optimization results show that the genetic algorithm has good global optimization ability， the optimization result improves the indicator of ride comfort and the vehicle′s performance.

Keywords： ride comfort； IFFT； time?domain simulation； Matlab； genetic algorithm

0 引 言

汽车行驶平顺性（简称平顺性）是指汽车在保持正常车速行驶过程中产生的振动和冲击环境对乘员舒适性的影响在一定界限内[1]。随着人们对汽车平顺性要求的不断提高，平顺性的研究已经深入到非线性动力学分析中，并通过建立非线性动力学模型来提高平顺性仿真的精度和优化的质量。然而，非线性系统不满足叠加原理，根据路面谱利用传递函数计算平顺性评价指标的频域分析方法已经不再适用，由此产生了多种路面不平的时域模拟方法[2?4]，用以进行平顺性时域仿真分析。平顺性仿真的目的是进行平顺性优化，力求进一步提高汽车的舒适性能。然而，现有的文献大多只进行了平顺性时域仿真，并未进行平顺性优化[5?7]。对此，本文采用IFFT法（逆快速傅里叶变换法）对路面不平度进行时域模拟，以某型号汽车线性振动系统为例，利用遗传算法对其进行优化。

遗传算法[8?10]（Genetic Algorithms，GA）是借鉴生物界自然选择和进化机制发展起来的高度并行、随机、自适应搜索算法。遗传算法具有很强的鲁棒性，不依赖问题的具体领域，特别适合处理传统方法难以解决的复杂非线性问题。随着Matlab软件的升级和函数的优化，遗传算法函数在适用性、可靠性、稳定性以及通用性方面都有了很大的提高和改善，由此成为了本文汽车平顺性优化的首选算法。

1 汽车五自由度动力学模型

1.1 力学模型

根据汽车的特点进行适当简化，简化由轮胎、悬架、车身和人椅组成的刚体系统，力学模型如图1所示。该模型有五个自由度，取广义坐标[zi（i=1，2，3，4，5）]，分别表示前簧下质量垂向位移、后簧下质量垂向位移、车身垂向位移、车身俯仰角位移和人椅垂向位移；[zg1]和[zg2]表示前后轮的路面不平激励。某型号汽车动力学参数如表1所示。

图1 汽车五自由度振动系统力学模型

表1 某型号汽车动力学参数

[＼&符号（单位）＼&数值＼&说明＼&物

理

参

数＼&[m1] /kg＼&40.5＼&前簧下质量＼&[m2] /kg＼&45.4＼&后簧下质量＼&[m3] /kg＼&700＼&车身质量＼&[Jxx] /（kg[?]m2）＼&1 200＼&车身绕横轴的转动惯量＼&[m4] /kg＼&80＼&人椅质量＼&力

学

参

数＼&[kt1] /（kN/m）＼&200＼&前轮刚度＼&[kt2] /（kN/m）＼&200＼&后轮刚度＼&[ks1] /（kN/m）＼&24＼&前悬架刚度＼&[ks2] /（kN/m）＼&19＼&后悬架刚度＼&[ks3] /（kN/m）＼&5＼&座椅刚度＼&[cs1] /（kN[?]s/m）＼&1.6＼&前悬架阻尼＼&[cs2] /（kN[?]s/m）＼&1.8＼&后悬架阻尼＼&[cs3] /（kN[?]s/m）＼&0.72＼&座椅阻尼＼&几

何

参

数＼&[l1] /m＼&1.25＼&车身质心至前轴的距离＼&[l2] /m＼&1.51＼&车身质心至后轴的距离＼&[l3] /m＼&0.5＼&车身质心至座椅中心的距离＼&]

1.2 动力学方程

汽车五自由度振动系统做平面运动，相对较为简单，故采用牛顿第二定律建立动力学方程：

[m1z1=-kt1z1+ks1（z3-z4l1-z1）+cs1（z3-z4l1-z1）] （1）

[ m2z2=-kt2z2+ks2（z3+z4l2-z2）+cs2（z3+z4l2-z2）] （2）

[m3z3=-ks1（z3-z4l1-z1）-cs1（z3-z4l1-z1）-ks2（z3+z4l2-z2）-cs2（z3+z4l2-z2）+ks3（z5-z3+z4l3）+cs3（z5-z3+z4l3）] （3）

[Jxxz4=ks1（z3-z4l1-z1）+cs1（z3-z4l1-z1）l1-ks2（z3+z4l2-z2）+cs2（z3+z4l2-z2）l2-ks3（z5-z3+z4l3）+cs3（z5-z3+z4l3）l3] （4）

[m4z5=-ks3（z5-z3+z4l3）-cs3（z5-z3+z4l3）] （5）

注意：本文在建立动力学方程时，之所以没有考虑弹性元件的原长和各部件本身的质量，是因为各个广义坐标是相对于各自的静平衡位置。

2 基于IFFT法的路面不平度时域模拟

路面不平度对汽车产生的激励具有一定的随机性，主要利用路面功率谱密度描述其统计特性。路面不平度的时域模拟大多是根据路面功率谱密度进行重构得到，时域模拟的主要方法有：谐波叠加法、滤波白噪声法、ARMA模型法、泊松（Poisson）法和IFFT法等。文献[11?13]中分别对这几种方法的优缺点进行了分析比较，并且指出IFFT法通过对功率谱密度进行离散采样，能够精确而又简单地重构道路的时域模型，是一种具有普适性的方法，它具有计算量小、计算简单高效等特点，能为后续车辆动力学仿真分析提供实时的时域模型[14]。对此，本文选用IFFT法进行时域模拟，利用Matlab语言开发了基于IFFT的时域模拟函数。

IFFT法基本思想是：

（1） 对随机激励的功率谱密度进行离散采样，根据功率谱密度的定义反求幅值谱；

（2） 生成随机相位；

（3） 利用逆快速傅里叶变换重构该随机信号的时域模型。

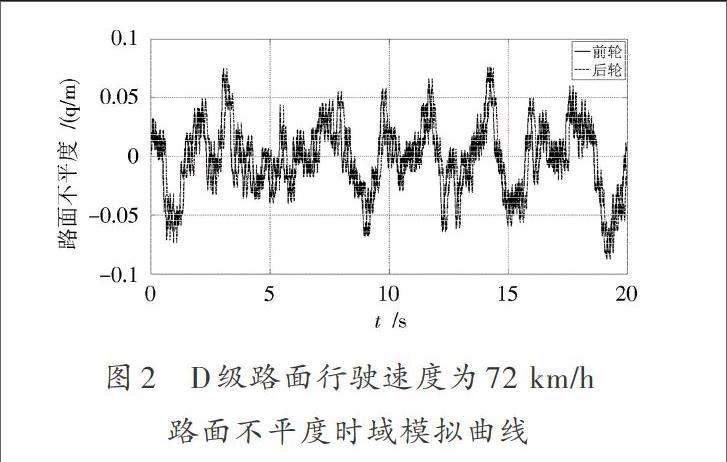
已知输入信号的功率谱密度函数，利用Matlab语言编制相应的程序，即可建立基于IFFT法路面随机输入的时域模型。图2为本文研究车型在D级路面行驶速度为72 km/h，路面不平的时域模拟曲线，仿真时间为20 s。

图2 D级路面行驶速度为72 km/h

路面不平度时域模拟曲线

从图2中可以看出后轮较前轮滞后时间约为0.137 s，这与实际时差[τ=Lv=]0.138 s十分吻合；根据时域模拟数据计算前后轮路面不平度均方根值分别为：0.030 4 m，0.030 4 m，这与文献[1]表中D级路面不平度几何平均值30.45 mm的结果也十分吻合，由此说明本文基于IFFT法建立的路面不平时域模拟结果是准确并且可靠的。

3 汽车五自由度动力学模型验证

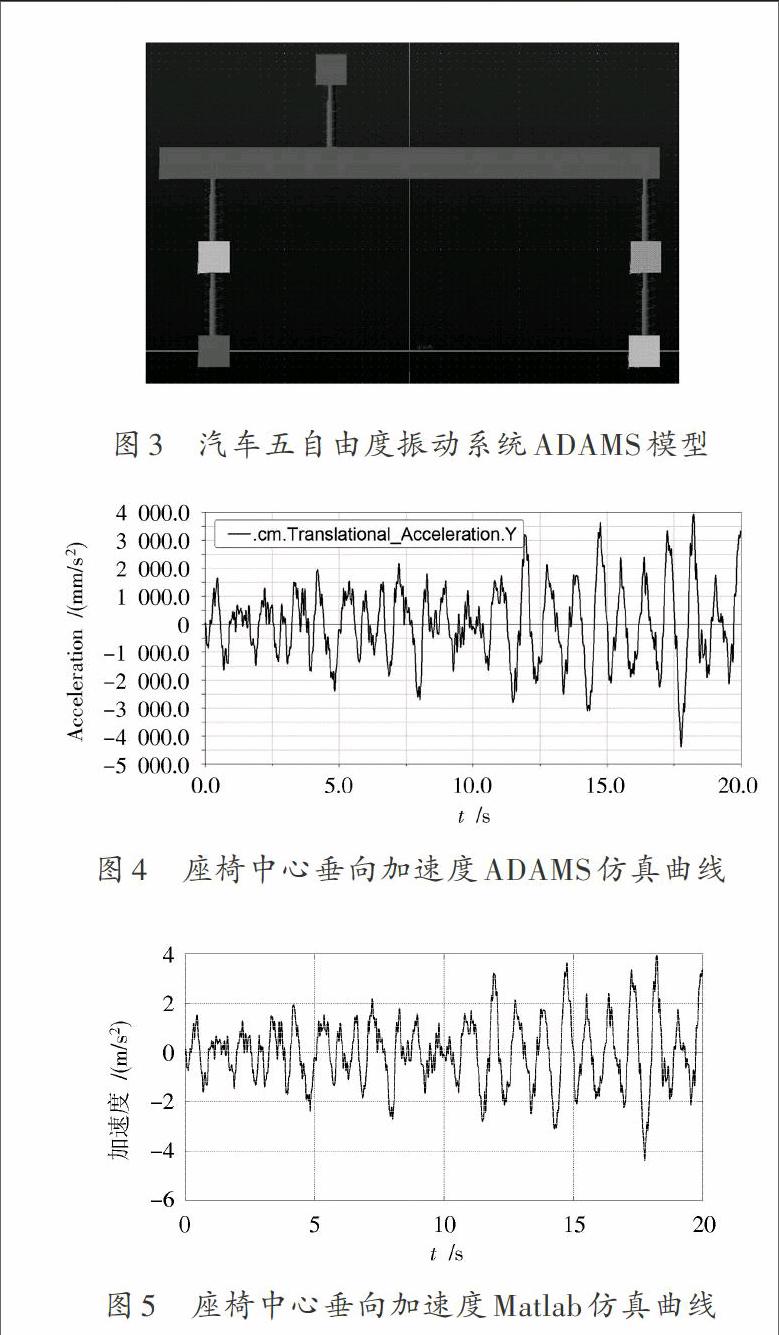
正确的汽车平顺性动力学模型是进行平顺性优化的前提。多体动力学分析软件ADAMS是机械系统动力学仿真分析的权威，故本文利用ADAMS对Matlab仿真结果进行验证。首先，在ADAMS中建立汽车五自由度动力学模型，并输入本文研究车型的动力学参数，如图3所示；然后，将IFFT法建立时域模拟的数据以txt文件形式导入ADAMS中作为前后轮路面激励，并进行动力学仿真；最后，查看座椅中心加速度仿真曲线，如图4所示。相同路面激励下座椅中心加速度Matlab仿真曲线如图5所示。其中，图4和图5均为D级路面行驶速度为72 km/h路面不平激励下的仿真曲线。

图3 汽车五自由度振动系统ADAMS模型

图4 座椅中心垂向加速度ADAMS仿真曲线

图5 座椅中心垂向加速度Matlab仿真曲线

将图4和图5曲线仔细对比可知，两者的仿真结果一模一样（注意两图加速度的单位），说明Matlab仿真结果是准确可信的，由此验证了本文建立的汽车五自由度动力学模型是准确可信的。

注意：ADAMS仿真与Matlab仿真均是以静平衡位置为初始状态进行的。

4 平顺性优化设计

4.1 优化工况

考虑到路面等级高且行驶速度高，或者路面等级低且行驶速度低，其动挠度、轮胎动载荷以及座椅中心加权加速度均方值较小，这些工况并无优化的必要。对此，本文对D级路面，行驶速度为50 km/h的工况进行平顺性优化设计，路面不平度时域模拟曲线如图6所示。

图6 D级路面行驶速度为50 km/h

路面不平度时域模拟曲线

4.2 设计变量

影响汽车平顺性的因素很多，如悬架参数、轮胎参数、座椅参数、整车的质量参数等。而轮胎参数、整车的质量参数和座椅参数多由厂家提供，改变困难，故本文选用前后悬架的刚度和阻尼作为优化的设计变量。

[x=ks1，ks2，cs1，cs2T] （6）

根据该型号汽车的特点，设计变量取值范围如表2所示。

表2 变量取值范围

[符号（单位）＼&下限＼&上限＼&[ks1] /（kN/m）＼&12.5＼&37.6＼&[ks2] /（kN/m）＼&10.8＼&32＼&[cs1] /（kN[?]s/m）＼&1.1＼&2.6＼&[cs2] /（kN[?]s/m）＼&0.9＼&2.3＼&]

4.3 目标函数

本文采用遗传算法进行平顺性优化设计，目标函数也称适应度函数。将座椅中心加权加速度均方根值作为目标函数，即：

[min f（x）=σz5] （7）

座椅中心加权加速度均方根值根据文献[1]的相关公式计算得到。

4.4 约束函数

（1） 悬架动挠度[fd]约束。悬架动挠度与其限位行程[[fd]]有关，若配合不当会增加撞击限位块的概率，致使平顺性变差。以撞击限位块的概率小于0.3%进行设计，此时要求悬架动挠度均方根值[σfd]应限制在[[fd]]的[13]之内[1]。根据相关标准，取[[fd]]为90 mm，由此得到前后悬架动挠度约束函数为：

[σfd1≤[fd]3] （8）

[σfd2≤[fd]3] （9）

（2） 轮胎与地面动载荷[Fd]的约束。当[Fd]的方向与静载[G]方向相反且大于静载[G]时，车轮会跳离地面，致使行驶安全性恶化。以车轮跳离地面的概率小于0.15%进行设计，此时要求轮胎相对动载荷均方根值[σFd]小于[G3][1]，由此得到前后轮胎与地面动载荷[Fd]的约束函数：

[σFd1≤G13] （10）

[σFd2≤G23] （11）

根据静力矩平衡，得到前后轮静载荷：

[G1=m3gl2+m4g（l2+l3）l1+l2+m1g] （12）

[G2=m3gl1+m4gl1-l3l1+l2+m2g] （13）

根据Parseval定理（信号在时域中计算的总能量等于其在频域中计算的总能量），式（8）～式（11）悬架动挠度和轮胎相对动载荷可通过计算时域数据均方根值得到。

4.5 遗传算法优化

ADAMS/View中并没有自带遗传算法优化函数，需要利用ADAMS提供的接口添加遗传算法程序。对此，本文采用Matlab优化工具箱的遗传算法函数进行优化。当确定设计变量、建立目标函数和约束函数后，利用优化工具箱中的遗传算法函数，即可求得所设定参数下的最优解。本文所设定的参数如下：初始种群为20，迭代代数为100，交叉概率为0.8，变异概率为0.1，图7为Matlab遗传算法优化界面。

优化界面中，左下角的Final point 即为遗传算法的优化结果，它表明设计变量取值为[x=][12.7，26.224，1.697，2.267]时，座椅中心加权加速度均方根值达到最小，其值为0.480 m/s2。

4.6 优化结果分析

为便于优化前后结果的对比分析，表3列出了优化前后的悬架参数，表4为优化前后平顺性评价指标的变化情况。图8为优化前后座椅中心垂向加速度时域响应曲线，图9为优化前后座椅中心垂向加速度功率谱密度曲线。

从表4中可以看出，优化后座椅中心加权加速度均方根值较优化前改善了21.3%，而悬架动挠度和轮胎与地面的动载荷变化较小，易验证优化后的悬架动挠度、轮胎与地面动载荷的均方根值均满足约束条件。

从图8和图9中可以看出，座椅中心加速度值和加速度功率谱密度值明显降低，说明优化后平顺性有了较大的改善。

5 结 论

本文建立了汽车五自由度振动力学模型和动力学方程，采用IFFT法对路面不平度进行时域模拟。然后，利用ADAMS验证了平顺性仿真模型。最后，以悬架刚度阻尼为设计变量，以悬架动挠度和轮胎相对动载荷为约束函数，以座椅中心加权加速度均方根值为目标函数，建立其优化模型，利用Matlab优化工具箱中的遗传算法函数进行优化。优化结果表明，利用遗传算法进行优化大大地提高了汽车的平顺性，为非线性振动系统平顺性时域仿真优化奠定了基础。

参考文献

[1] 余志生.汽车理论[M].5版.北京：机械工业出版社，2009.

[2] 陈杰平，陈无畏，祝辉，等.基于Matlab/Simulink的随机路面建模与不平度仿真[J].农业机械学报，2010，41（3）：11?15.

[3] 金睿臣，宋健.路面不平度的模拟与汽车非线性随机振动的研究[J].清华大学学报（自然科学版），1999，39（8）：77?80.

[4] 张立军，张天侠.车辆四轮相关时域随机输入通用模型的研究[J].农业机械学报，2005，36（12）：29?31.

[5] 张鄂，刘中华，邵晓春.九自由度乘坐动力学模型的人体振动特性仿真[J].交通运输工程学报，2010，10（4）：58?64.

[6] LE V Q，张建润，王园，等.基于三维动力学模型的重型卡车动态参数对平顺性的影响[J].东南大学学报（自然科学版），2013，43（4）：763?770.

[7] 陈克，高洁，吕周泉.基于虚拟试验场技术的汽车平顺性仿真分析[J].中国工程机械学报，2010，8（2）：208?212.

[8] GOLDBERG D E. Genetic algorithms in search， optimization， and machine learning [M]. Boston： Addison Wesley， 1989.

[9] HOLLAND J H. Adaptation in natural and artificial systems： an introductory analysis with applications to biology， control， and artificial intelligence [M]. Michigan： Michigan Press， 1975.

[10] 戴晓晖，李敏强，寇纪淞.遗传算法理论研究综述[J].控制与决策，2000，15（3）：263?268.

[11] 姜丽丽.基于傅里叶反变换的路面随机激励时域建模与仿真[D].长春：吉林大学，2007.

[12] 彭佳，何杰，李旭宏，等.路面不平度随机激励时域模型的仿真比较与评价[J].解放军理工大学学报（自然科学版），2009，10（1）：77?82.

[13] 张永林.车辆道路数值模拟与仿真研究[D].武汉：华中科技大学，2010.

[14] 何宁，石成英，周保顺.路面不平度时域模型模拟方法研究[J].环境技术，2014，32（3）：50?51.